东方资产营销网站/seo策略工具

1. 题目

906. 超级回文数

2. 解题思路

题目意思很简单，在给定范围中找到所有满足，它本身是回文，且它的平方也是回文的数字个数。
这题需要注意题目给定的范围，后面很有用：

因为回文范围是有限的，那么我们可以先初始化基础情况，也就是枚举出单个数字，和两位数字的回文。
题目要求范围大于1，那么我们枚举的基础数字就是1-9，通过下面的代码就可以初始化好基础的回文。

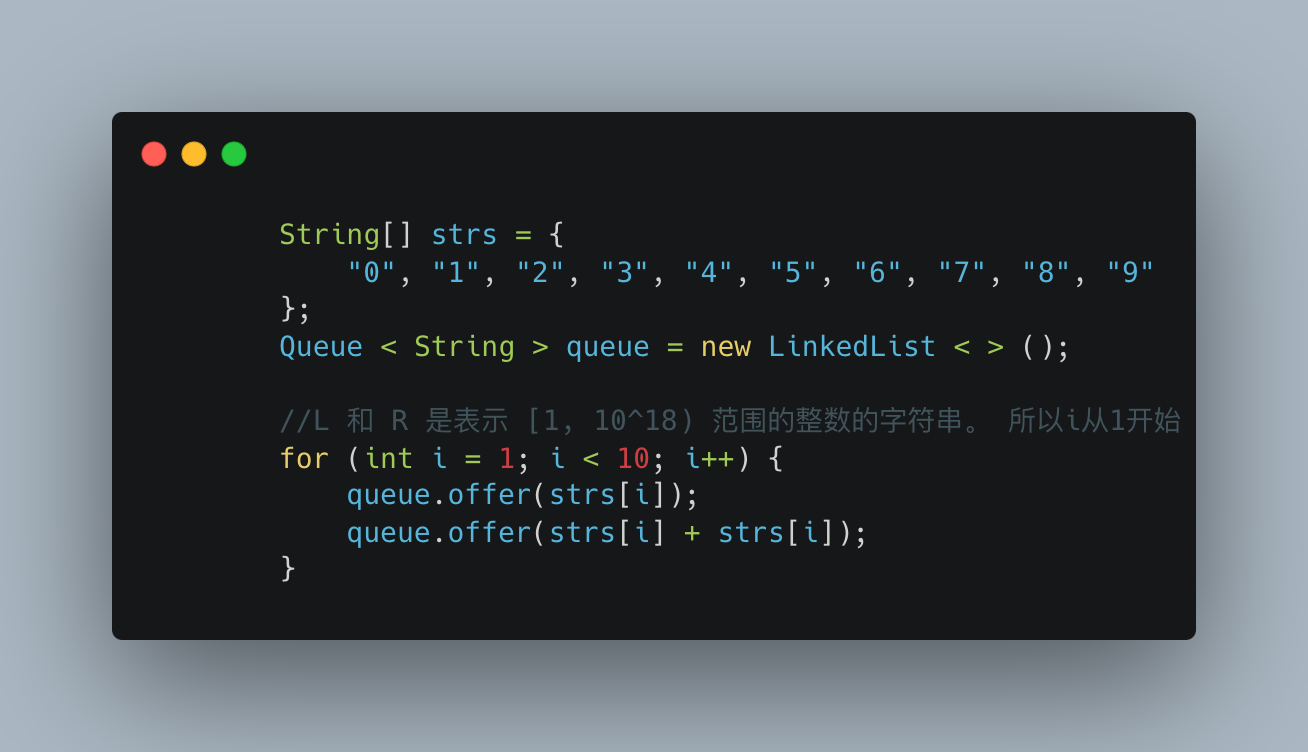
然后我们针对每个回文进行判断，它的平方是不是回文，如果是就给结果加一。
如果当前回文数的长度是偶数，继续通过在中间插入一个或两个字符（从’0’到’9’）来生成新的、更长的回文数，并将它们加入队列。这样能够递归生成长度更长的回文数。
如果当前回文数的平方已经超出了范围 [left, right]，则停止处理该回文数。
最后统计结果就好了。

注意：上面的代码在LC可以通过，但是在PAT有些用例会超出内存限制，所以下面进行一版优化：
整理思路方向不变，还是通过遍历生成回文数来判断，做如下优化：

• 直接通过构建回文数的前半部分，然后反转其一部分生成完整的回文数。这避免了逐步拼接字符串的过程，提高了效率。
• 循环从1到10位生成回文数，并且限制了每个回文数的生成长度。通过计算有效的起始和结束范围（start 和 end），确保生成的数字合理。
• 在生成每个回文数的平方后，立即检查其是否超过上限 R，如果超过，立刻停止后续的生成过程。

3. 代码

3.1. 注意点

[!NOTE] 1、19行的tmp.length() > 10 这个判断条件是啥意思
[1, 10^18) 是题目给定的整数范围，超过这个范围的数值不需要再检查。而数字的长度超过10位的平方肯定超过了这个范围。
回文数长度达到11位，那么它的平方就会超过 10^22，远远超出题目要求的范围 10^18

[!NOTE] 2、24行的if (tmpNum * tmpNum < 0) 这个判断条件是啥意思
我们的tmpNum类型为Long，当tmpNum * tmpNum 的结果超过Long的最大值，那么就会溢出成负数，这种情况也没必要处理了。

[!NOTE] 3、为什么在处理当前数字为偶数的时候要插入字符，并且只插入1、2个字符，不插入3、4、5…个
因为回文是数字对称的，它往往可以直接在当前回文上进行插入来得到新回文，处理代码会尝试在当前偶数长度的回文数中间插入一个或两个数字，生成更长的回文数。这样做的目的是生成可能符合条件的下一个更长的回文数，并且保持回文数的对称性。

• 插入一个 字符：生成奇数长度的回文数。例如从 "1221" 生成 "12321"，这个新回文数的长度是奇数。
• 插入两个相同的 字符：生成偶数长度的回文数。例如从 "1221" 生成 "123321"，这个新回文数的长度是偶数。
  这种方式已经覆盖了常见的奇数和偶数长度回文数的情况，不需要再增加额外的插入方式。

[!NOTE] 4、32行统计的答案是tmp还是tmp的平方？
答案是tmpNum*tmpNum
题目定义：如果一个正整数自身是回文数，而且它也是一个回文数的平方，那么我们称这个数为超级回文数。
所以tmpNum*tmpNum代表它是tmpNum的平方，所以tmpNum*tmpNum才是超级回文数

3.2. 完整代码

class Solution {public int superpalindromesInRange(String left, String right) {Long l = Long.parseLong(left);Long r = Long.parseLong(right);int res = 0;String[] strs = {"0", "1", "2", "3", "4", "5", "6", "7", "8", "9"};Queue < String > queue = new LinkedList < > ();//L 和 R 是表示 [1, 10^18) 范围的整数的字符串。 所以i从1开始for (int i = 1; i < 10; i++) {queue.offer(strs[i]);queue.offer(strs[i] + strs[i]);}while (!queue.isEmpty()) {String tmp = queue.poll();if (tmp.length() > 10) {continue;}Long tmpNum = Long.parseLong(tmp);//处理溢出情况，tmp的平方有可能会大于Long的最大值if (tmpNum * tmpNum < 0) {continue;}if (tmpNum * tmpNum <= r) {StringBuilder sb = new StringBuilder();sb.append(tmpNum * tmpNum);//判断当前数字的平方是不是回文if (tmpNum * tmpNum >= l && sb.toString().equals(sb.reverse().toString())) {res++;}if (tmp.length() % 2 == 0) {//向当前回文数插入数字构造新的更长的回文数for (String c: strs) {queue.offer(tmp.substring(0, tmp.length() / 2) + c + tmp.substring(tmp.length() / 2));queue.offer(tmp.substring(0, tmp.length() / 2) + c + c + tmp.substring(tmp.length() / 2));}}}}return res;}
}

3.2.1. PAT完整代码

[!NOTE] 解释下新的核心代码，即17行开始的for循环
1、外层循环for (int length = 1; length <= 10; length++) ：代表生成1-10位的回文数，为啥是10位呢？
题目要求的范围是[1, 10^18) ，10位数的平方已经超过这个范围了
2、起始和结束范围：通过计算范围来确定生成的数字范围，比如长度为2，那范围就是10-99

• 计算起始值：
• int start = (int) Math.pow(10, halfLength - 1);
• 这行代码计算当前半长度的最小值。
• 例如：
• 当 halfLength = 1，start = 10^0 = 1，表示从1开始。
• 当 halfLength = 2，start = 10^1 = 10，表示从10开始。
• 当 halfLength = 3，start = 10^2 = 100，表示从100开始。
• 计算结束值：int end = (int) Math.pow(10, halfLength);
• 这行代码计算当前半长度的下一个值（不包括在内，通过for循环的结束条件来控制不包括在内）。
• 例如：
• 当 halfLength = 1，end = 10^1 = 10，表示到9为止。
• 当 halfLength = 2，end = 10^2 = 100，表示到99为止。
• 当 halfLength = 3，end = 10^3 = 1000，表示到999为止。

3、生成回文数：
循环遍历从 start 到 end 的所有数，构建回文数：

• firstHalf 是前半部分（例如，123 的前半部分是 12）。
• secondHalf 是前半部分的反转（例如，12 反转为 21），并与前半部分拼接成完整的回文数（例如，121）。

4、后续处理：
后续就判断该数字是否超过题目范围，以及它的平方数是不是回文，如果是，那它的平方数就是一个超级回文数
5、int halfLength = (length + 1) / 2为什么要加一
它为了处理奇数长度的情况，确保在生成回文时能够正确地获取中间的数字。例如，对于长度为 5 的回文，(5 + 1) / 2 结果为 3，这样可以包含中间的数字。
6、square > R后为什么直接break？
和LC的解法不同，PAT的解法是直接从小到大遍历的，当前的数据超出范围了，它后面的数据比它大，肯定也会超出范围，所以直接break
7、为什么firstPath.substring(0,length/2)不是firstPath.substring(0,firstPath.length()/2)

import java.util.*;
import java.util.stream.Collectors;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);List<Long> in = Arrays.stream(sc.nextLine().split(",")).map(Long::valueOf).collect(Collectors.toList());long L = in.get(0);long R = in.get(1);List<Long> res = new ArrayList<>();// 从1到10位的数字开始生成回文数for (int length = 1; length <= 10; length++) {int halfLength = (length + 1) / 2;//Math.pow：10的halfLength - 1次方int start = (int) Math.pow(10, halfLength - 1);int end = (int) Math.pow(10, halfLength);for (int i = start; i < end; i++) {String firstHalf = Integer.toString(i);StringBuilder secondHalf = new StringBuilder(firstHalf.substring(0, length / 2)).reverse();String palindrome = firstHalf + secondHalf.toString();long num = Long.parseLong(palindrome);long square = num * num;if (square > R) {break; // 剪枝：平方数超过R时停止}if (square >= L && isPalindrome(Long.toString(square))) {res.add(square);}}}Collections.sort(res);System.out.println(res);}// 判断是否是回文数private static boolean isPalindrome(String s) {int left = 0;int right = s.length() - 1;while (left < right) {if (s.charAt(left) != s.charAt(right)) {return false;}left++;right--;}return true;}
}