高级算法设计与分析 学习笔记10 平摊分析

动态表,可以变长。

一溢出就另起一个两倍大小的表。
可以轻易证明把n个数字放进去的时间复杂度是O(n),n + n/2 + n/4……也就2n,插入数字本身也就是n,加起来最多不超过3n.
这种复杂度究竟是怎么算的?毕竟每次插入复杂度不一样,怎么算平均呢?



当然,计算平摊不只有这种方法:

银行法:


势能法:

把存款当成当前集合的势能。



首尾相连很多都被抵掉了。
使用势能法分析之前的动态表,怎么说?:

势能和存款就是一个意思。
问题:这些什么存款,势能的,一次多少究竟是怎么算出来的?
答曰:先用最开始的方法算出来总体的复杂度,然后凑。
相关文章:

高级算法设计与分析 学习笔记10 平摊分析
动态表,可以变长。 一溢出就另起一个两倍大小的表。 可以轻易证明把n个数字放进去的时间复杂度是O(n),n n/2 n/4……也就2n,插入数字本身也就是n,加起来最多不超过3n. 这种复杂度究竟是怎么算的?毕竟每次插入复杂度…...

从“纸面算力”到“好用算力”,超聚变打通AI+“最后一公里”
如果要评选2024年的年度科技名词,AI当属最热门的候选项。 年初的《政府工作报告》中首次提出了“人工智能”行动,正在从顶层设计着手,加快形成以人工智能为引擎的新质生产力。 折射到市场层面,AI作为一种新的范式,不…...

【有啥问啥】具身智能(Embodied AI):人工智能的新前沿
具身智能(Embodied AI):人工智能的新前沿 引言 在人工智能(AI)的进程中,具身智能(Embodied AI)正逐渐成为研究与应用的焦点。具身智能不仅关注于机器的计算能力,更强调…...

11-pg内核之锁管理器(六)死锁检测
概念 每个事务都在等待集合中的另一事务,由于这个集合是一个有限集合,因此一旦在这个等待的链条上产生了环,就会产生死锁。自旋锁和轻量锁属于系统锁,他们目前没有死锁检测机制,只能靠内核开发人员在开发过程中谨慎的…...

Git 与标签管理
在 Git 中,标签 tag 是指向某个 commit 的指针(所以创建和删除都很快)。Git 有 commit id 了,为什么还要有 tag?commit id 是一串无规律的数字,不好记;而 tag 是我们自定义的,例如我…...
初始化 MyPgXact)
【0334】Postgres内核之 auxiliary process(辅助进程)初始化 MyPgXact
1. MyPgXact(ProcGlobal->allPgXact)间接初始化 在上一篇文章【0333】Postgres内核之 auxiliary process(辅助进程)创建 PGPROC 中, 讲解了Postgres内核完成 AuxiliaryProcess 初始化 pid、lxid、procLatch、myProcLocks、lockGroupMembers等所有成员的过程。 这些成员…...

20.1 分析pull模型在k8s中的应用,对比push模型
本节重点介绍 : push模型和pull模型监控系统对比为什么在k8s中只能用pull模型的k8s中主要组件的暴露地址说明 push模型和pull模型监控系统 对比下两种系统采用的不同采集模型,即push型采集和pull型采集。不同的模型在性能的考虑上是截然不同的。下面表格简单的说…...

Ubuntu 镜像替换为阿里云镜像:简化你的下载体验
Ubuntu,作为一款广受欢迎的Linux发行版,以其稳定性和易用性著称。但你是否曾因为下载速度慢而感到沮丧?现在,你可以通过将Ubuntu的默认下载源替换为阿里云镜像来解决这个问题。本文将指导你如何完成这一过程。 为什么选择阿里云镜…...

The Sandbox 游戏制作教程第 6 章|如何使用装备制作出色的游戏 —— 避免环境危险
欢迎回到我们的系列,我们将记录 The Sandbox Game Maker 的 “On-Equip”(装备)功能的多种用途。 如果你刚加入 The Sandbox,装备功能是 “可收集组件”(Collectable Component)中的一个多功能工具…...

JavaScript中的输出方式
1. console.log() console.log() 是开发者在调试代码时最常用的方法。它将信息打印到浏览器的控制台,使开发者能够查看变量的值、程序的执行状态以及其他有用的信息。 用途:用于调试和记录程序运行时的信息。优点:简单易用,适合…...

力扣9.25
2306. 公司命名 给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下: 从 ideas 中选择 2 个 不同 名字,称为 ideaA 和 ideaB 。 交换 ideaA 和 ideaB 的首字母。 如果得到的两个新名字 都 不在ideas 中,那么 …...

从零开始之AI面试小程序
从零开始之AI面试小程序 文章目录 从零开始之AI面试小程序前言一、工具列表二、开发部署流程1. VMWare安装2. Centos安装3. Centos环境配置3.1. 更改子网IP3.2. 配置静态IP地址 4. Docker和Docker Compose安装5. Docker镜像加速源配置6. 部署中间件6.1. MySQL部署6.2. Redis部署…...
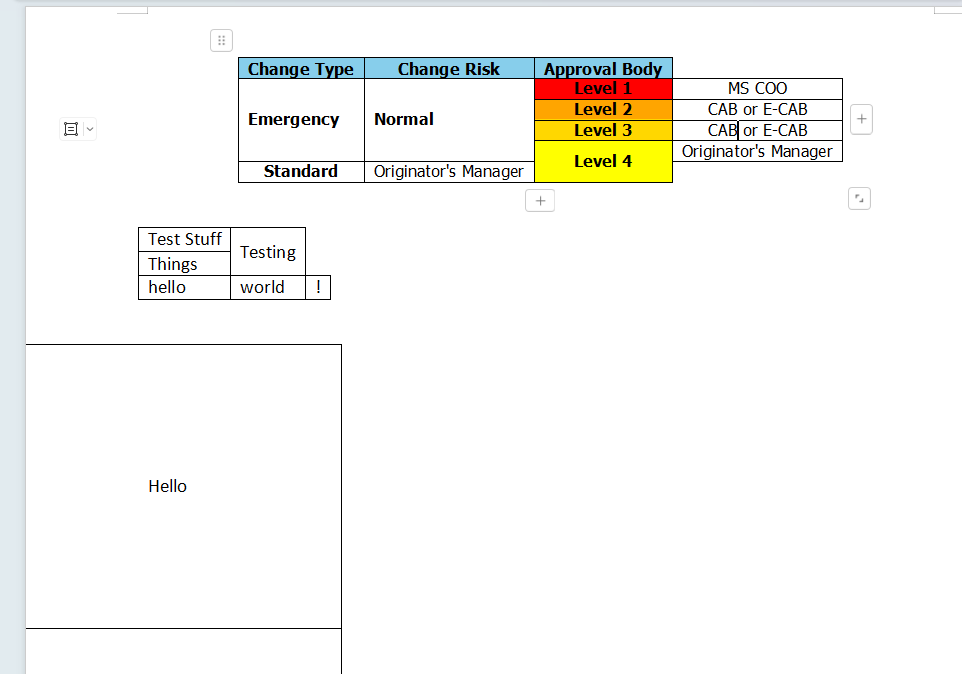
Html2OpenXml:HTML转化为OpenXml的.Net库,轻松实现Html转为Word。
推荐一个开源库,轻松实现HTML转化为OpenXml。 01 项目简介 Html2OpenXml 是一个开源.Net库,旨在将简单或复杂的HTML内容转换为OpenXml组件。 该项目始于2009年,最初是为了将用户评论转换为Word文档而设计的 随着时间的推移,Ht…...

HumanNeRF:Free-viewpoint Rendering of Moving People from Monocular Video 精读
1. 姿态估计和骨架变换模块 人体姿态估计:HumanNeRF 通过已知的单目视频对视频中人物的姿态进行估计。常见的方法是通过人体姿态估计器(如 OpenPose 或 SMPL 模型)提取人物的骨架信息,获取 3D 关节的位置信息。这些关节信息可以帮…...
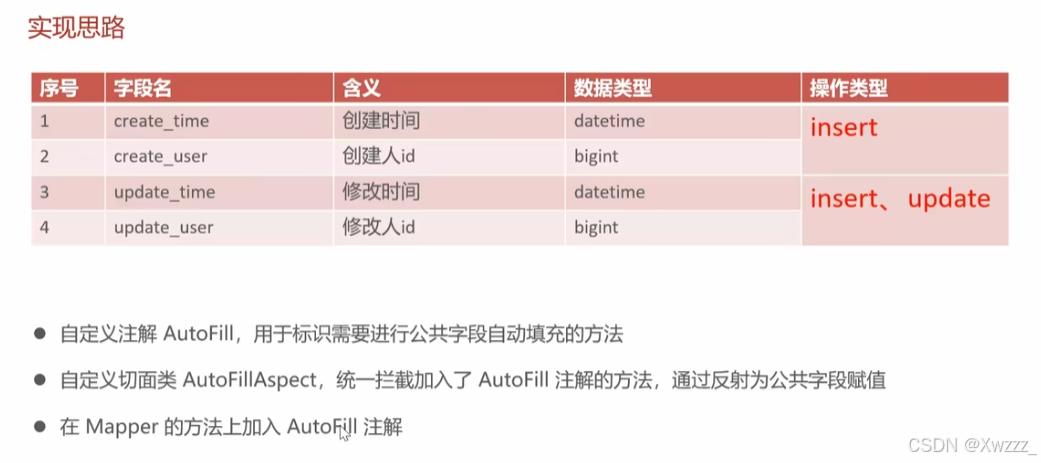
Springboot中基于注解实现公共字段自动填充
1.使用场景 当我们有大量的表需要管理公共字段,并且希望提高开发效率和确保数据一致性时,使用这种自动填充方式是很有必要的。它可以达到一下作用 统一管理数据库表中的公共字段:如创建时间、修改时间、创建人ID、修改人ID等,这些…...

Android 已经过时的方法用什么新方法替代?
过时修正举例 (Kotlin): getColor(): resources.getColor(R.color.white) //已过时// 修正后:ContextCompat.getColor(this, R.color.white) getDrawable(): resources.getDrawable(R.mipmap.test) //已过时//修正后:ContextCompat.getDrawable(this, R.mipmap.test) //…...

【RocketMQ】MQ与RocketMQ介绍
🎯 导读:本文介绍了消息队列(MQ)的基本概念及其在分布式系统中的作用,包括实现异步通信、削峰限流和应用解耦等方面的优势,并对ActiveMQ、RabbitMQ、RocketMQ及Kafka四种MQ产品进行了对比分析,涵…...
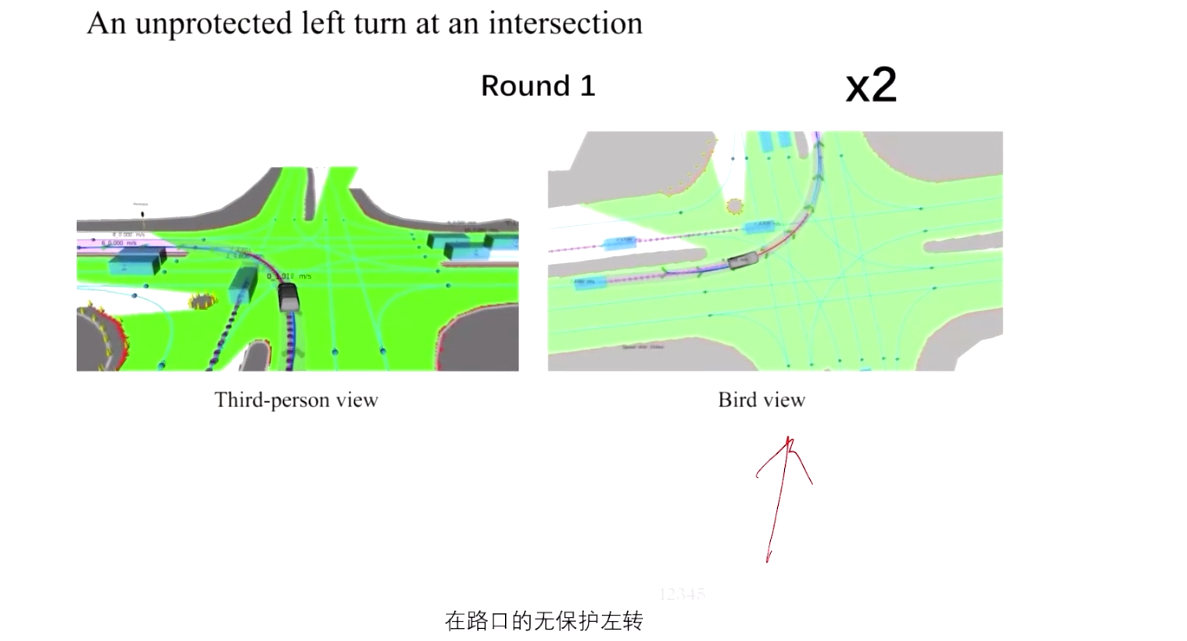
【笔记】自动驾驶预测与决策规划_Part4_时空联合规划
文章目录 0. 前言1. 时空联合规划的基本概念1.1 时空分离方法1.2 时空联合方法 2.基于搜索的时空联合规划 (Hybrid A* )2.1 基于Hybrid A* 的时空联合规划建模2.2 构建三维时空联合地图2.3 基于Hybrid A*的时空节点扩展2.4 Hybrid A* :时空节…...

Linux指令收集
文件和目录操作 ls: 列出目录内容。 -l 显示详细信息。-a 显示隐藏文件(以.开头的文件)。cd: 改变当前工作目录。 cd ~ 返回主目录。cd .. 上移一级目录。pwd: 显示当前工作目录。mkdir: 创建目录。 mkdir -p path/to/directory 创建多级目录。rmdir: 删…...
)
《C++并发编程实战》笔记(五)
五、内存模型和原子操作 5.1 C中的标准原子类型 原子操作是不可分割的操作,它或者完全做好,或者完全没做。 标准原子类型的定义在头文件<atomic>中,类模板std::atomic<T>接受各种类型的模板实参,从而创建该类型对应…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...
