条件熵公式详细解释、举例说明计算步骤
公式 7-4 是条件熵的表达式:
E ( Y ∣ X ) = ∑ i = 1 m p ( X = x i ) E ( Y ∣ X = x i ) E(Y|X) = \sum_{i=1}^m p(X = x_i) E(Y | X = x_i) E(Y∣X)=i=1∑mp(X=xi)E(Y∣X=xi)
这个公式表示的是条件熵,它是衡量在已知某一特征 X X X 的情况下,随机变量 Y Y Y 的不确定性(熵)。条件熵 E ( Y ∣ X ) E(Y|X) E(Y∣X) 的含义是:在已知 X X X 的值的情况下, Y Y Y 的不确定性有多大。它通过对所有可能的 X X X 的取值的熵进行加权平均来计算。
公式的详细解释:
-
E ( Y ∣ X ) E(Y|X) E(Y∣X):这是条件熵,表示在给定 X X X 的条件下, Y Y Y 的不确定性。它衡量了已知 X X X 的值后, Y Y Y 仍然有多少不确定性。如果 X X X 对 Y Y Y 的影响很大,那么条件熵会很低;如果 X X X 无法有效区分 Y Y Y 的类别,那么条件熵会较高。
-
∑ i = 1 m \sum_{i=1}^m ∑i=1m:这个符号表示对 X X X 的所有可能取值进行求和。即我们对 X X X 的每一个取值 x i x_i xi 都要计算相应的条件熵并加权平均。 m m m 是随机变量 X X X 的可能取值数量。
-
p ( X = x i ) p(X = x_i) p(X=xi):这是边缘概率,表示 X X X 取某个值 x i x_i xi 的概率。它表示了在数据集中 X X X 取值为 x i x_i xi 的样本所占比例。
-
E ( Y ∣ X = x i ) E(Y|X = x_i) E(Y∣X=xi):这是在 X X X 已知为 x i x_i xi 的条件下, Y Y Y 的熵,即条件熵。它衡量了在 X = x i X = x_i X=xi 的条件下, Y Y Y 的不确定性。通常,条件熵使用公式 E ( Y ∣ X = x i ) = − ∑ j = 1 n p ( Y = y j ∣ X = x i ) log p ( Y = y j ∣ X = x i ) E(Y|X = x_i) = - \sum_{j=1}^n p(Y = y_j | X = x_i) \log p(Y = y_j | X = x_i) E(Y∣X=xi)=−∑j=1np(Y=yj∣X=xi)logp(Y=yj∣X=xi) 来计算,其中 p ( Y = y j ∣ X = x i ) p(Y = y_j | X = x_i) p(Y=yj∣X=xi) 是条件概率,表示在 X = x i X = x_i X=xi 时 Y Y Y 为 y j y_j yj 的概率。
直观理解条件熵:
-
条件熵 E ( Y ∣ X ) E(Y|X) E(Y∣X) 表示在已知 X X X 的情况下, Y Y Y 还有多少不确定性。如果 X X X 能完全决定 Y Y Y 的取值,那么条件熵 E ( Y ∣ X ) E(Y|X) E(Y∣X) 为 0,表示没有不确定性(即 X X X 和 Y Y Y 完全相关)。如果 X X X 和 Y Y Y 完全无关,则条件熵 E ( Y ∣ X ) E(Y|X) E(Y∣X) 等于 Y Y Y 的熵 E ( Y ) E(Y) E(Y),即条件熵没有帮助减少不确定性。
-
条件熵是信息增益的基础:当我们使用某个特征 X X X 来划分数据时,条件熵表示在这个划分下,目标变量 Y Y Y 的不确定性。如果某个划分显著减少了不确定性(即条件熵小),说明这个特征 X X X 是一个很好的分类依据。
举例说明:
假设我们有一个简单的二元分类问题, Y Y Y 表示分类标签, X X X 表示一个特征。我们有以下数据集:
- 数据集包含 10 个样本,其中 6 个是类别 1,4 个是类别 2。
- 特征 X X X 可以取 2 个值: x 1 x_1 x1 和 x 2 x_2 x2。
- 当 X = x 1 X = x_1 X=x1 时,有 4 个样本,其中 3 个是类别 1,1 个是类别 2。
- 当 X = x 2 X = x_2 X=x2 时,有 6 个样本,其中 3 个是类别 1,3 个是类别 2。
1. 计算边缘概率:
- p ( X = x 1 ) = 4 10 = 0.4 p(X = x_1) = \frac{4}{10} = 0.4 p(X=x1)=104=0.4
- p ( X = x 2 ) = 6 10 = 0.6 p(X = x_2) = \frac{6}{10} = 0.6 p(X=x2)=106=0.6
2. 计算条件熵 E ( Y ∣ X = x 1 ) E(Y|X = x_1) E(Y∣X=x1) 和 E ( Y ∣ X = x 2 ) E(Y|X = x_2) E(Y∣X=x2):
条件熵的计算公式为:
E ( Y ∣ X = x i ) = − ∑ j = 1 n p ( Y = y j ∣ X = x i ) log p ( Y = y j ∣ X = x i ) E(Y|X = x_i) = - \sum_{j=1}^n p(Y = y_j | X = x_i) \log p(Y = y_j | X = x_i) E(Y∣X=xi)=−j=1∑np(Y=yj∣X=xi)logp(Y=yj∣X=xi)
-
当 X = x 1 X = x_1 X=x1 时:
- 类别 1 的条件概率: p ( Y = 1 ∣ X = x 1 ) = 3 4 = 0.75 p(Y = 1 | X = x_1) = \frac{3}{4} = 0.75 p(Y=1∣X=x1)=43=0.75
- 类别 2 的条件概率: p ( Y = 2 ∣ X = x 1 ) = 1 4 = 0.25 p(Y = 2 | X = x_1) = \frac{1}{4} = 0.25 p(Y=2∣X=x1)=41=0.25
条件熵为:
E ( Y ∣ X = x 1 ) = − ( 0.75 log 2 0.75 + 0.25 log 2 0.25 ) E(Y|X = x_1) = - (0.75 \log_2 0.75 + 0.25 \log_2 0.25) E(Y∣X=x1)=−(0.75log20.75+0.25log20.25)我们计算各项的对数值:
log 2 0.75 ≈ − 0.415 , log 2 0.25 = − 2 \log_2 0.75 \approx -0.415, \quad \log_2 0.25 = -2 log20.75≈−0.415,log20.25=−2代入公式:
E ( Y ∣ X = x 1 ) = − ( 0.75 × − 0.415 + 0.25 × − 2 ) = 0.31125 + 0.5 = 0.81125 E(Y|X = x_1) = - (0.75 \times -0.415 + 0.25 \times -2) = 0.31125 + 0.5 = 0.81125 E(Y∣X=x1)=−(0.75×−0.415+0.25×−2)=0.31125+0.5=0.81125 -
当 X = x 2 X = x_2 X=x2 时:
- 类别 1 的条件概率: p ( Y = 1 ∣ X = x 2 ) = 3 6 = 0.5 p(Y = 1 | X = x_2) = \frac{3}{6} = 0.5 p(Y=1∣X=x2)=63=0.5
- 类别 2 的条件概率: p ( Y = 2 ∣ X = x 2 ) = 3 6 = 0.5 p(Y = 2 | X = x_2) = \frac{3}{6} = 0.5 p(Y=2∣X=x2)=63=0.5
条件熵为:
E ( Y ∣ X = x 2 ) = − ( 0.5 log 2 0.5 + 0.5 log 2 0.5 ) E(Y|X = x_2) = - (0.5 \log_2 0.5 + 0.5 \log_2 0.5) E(Y∣X=x2)=−(0.5log20.5+0.5log20.5)因为 log 2 0.5 = − 1 \log_2 0.5 = -1 log20.5=−1,所以:
E ( Y ∣ X = x 2 ) = − ( 0.5 × − 1 + 0.5 × − 1 ) = 1 E(Y|X = x_2) = - (0.5 \times -1 + 0.5 \times -1) = 1 E(Y∣X=x2)=−(0.5×−1+0.5×−1)=1
3. 计算条件熵 E ( Y ∣ X ) E(Y|X) E(Y∣X):
现在我们将两个条件熵按边缘概率加权求和:
E ( Y ∣ X ) = p ( X = x 1 ) E ( Y ∣ X = x 1 ) + p ( X = x 2 ) E ( Y ∣ X = x 2 ) E(Y|X) = p(X = x_1) E(Y|X = x_1) + p(X = x_2) E(Y|X = x_2) E(Y∣X)=p(X=x1)E(Y∣X=x1)+p(X=x2)E(Y∣X=x2)
代入已知数值:
E ( Y ∣ X ) = 0.4 × 0.81125 + 0.6 × 1 = 0.3245 + 0.6 = 0.9245 E(Y|X) = 0.4 \times 0.81125 + 0.6 \times 1 = 0.3245 + 0.6 = 0.9245 E(Y∣X)=0.4×0.81125+0.6×1=0.3245+0.6=0.9245
结论:
- 条件熵 E ( Y ∣ X ) = 0.9245 E(Y|X) = 0.9245 E(Y∣X)=0.9245 表示,在已知特征 X X X 的情况下,目标变量 Y Y Y 仍然具有约 0.9245 的不确定性。
- 条件熵帮助我们理解特征 X X X 对目标变量 Y Y Y 的解释能力。如果某个特征的条件熵很低,说明这个特征可以很好地帮助分类决策。如果条件熵很高,则说明该特征对目标变量的区分能力有限。
总结:
- 公式 7-4 计算了条件熵,它衡量了在已知特征 X X X 的情况下,目标变量 Y Y Y 的不确定性。
- 条件熵是决策树中进行特征选择的重要指标,通过最小化条件熵,我们可以选择出能够最好地分类数据的特征。
- 条件熵越小,表示特征 X X X 能很好地解释目标变量 Y Y Y 的分类。
相关文章:

条件熵公式详细解释、举例说明计算步骤
公式 7-4 是条件熵的表达式: E ( Y ∣ X ) ∑ i 1 m p ( X x i ) E ( Y ∣ X x i ) E(Y|X) \sum_{i1}^m p(X x_i) E(Y | X x_i) E(Y∣X)i1∑mp(Xxi)E(Y∣Xxi) 这个公式表示的是条件熵,它是衡量在已知某一特征 X X X 的情况下,…...

颍川陈氏始祖陈寔逆势崛起的原由(一)不屈的努力
园子说颍川 按陈寔的出身,与当官是风马牛不相及的。 东汉末年的社会,朝中外戚、宦官当道,地方则由世家大族把持,郡县的政治经济资源都由他们掌控分配,平民以及中小地主很难有出头之日,弄不好就被兼并了。…...

golang小项目1-家庭收支记账系统
项目地址:golang小项目 参考资料:尚硅谷golang教程P229 家庭收支记账系统 1. 系统简介 1.1 项目背景 在现代社会中,家庭的财务管理显得尤为重要。随着生活成本的不断上升,家庭需要有效地记录和分析收支情况,以确保…...

Visual Studio Code下载安装及汉化
官网:https://code.visualstudio.com/ 按照指示一步步操作即可: 汉化:...

MySQL—触发器详解
基本介绍 触发器是与表有关的数据库对象,在 INSERT、UPDATE、DELETE 操作之前或之后触发并执行触发器中定义的 SQL 语句。 触发器的这种特性可以协助应用在数据库端确保数据的完整性、日志记录、数据校验等操作。 使用别名 NEW 和 OLD 来引用触发器中发生变化的记…...
钉钉H5微应用Springboot+Vue开发分享
文章目录 说明技术路线注意操作步骤思路图 一、创建钉钉应用二、创建java项目三、创建vue项目(或uniapp项目),npm引入sdk的依赖四、拥有公网域名端口。开发环境可以使用(贝锐花生壳等工具)五、打开钉钉开发者平台&…...
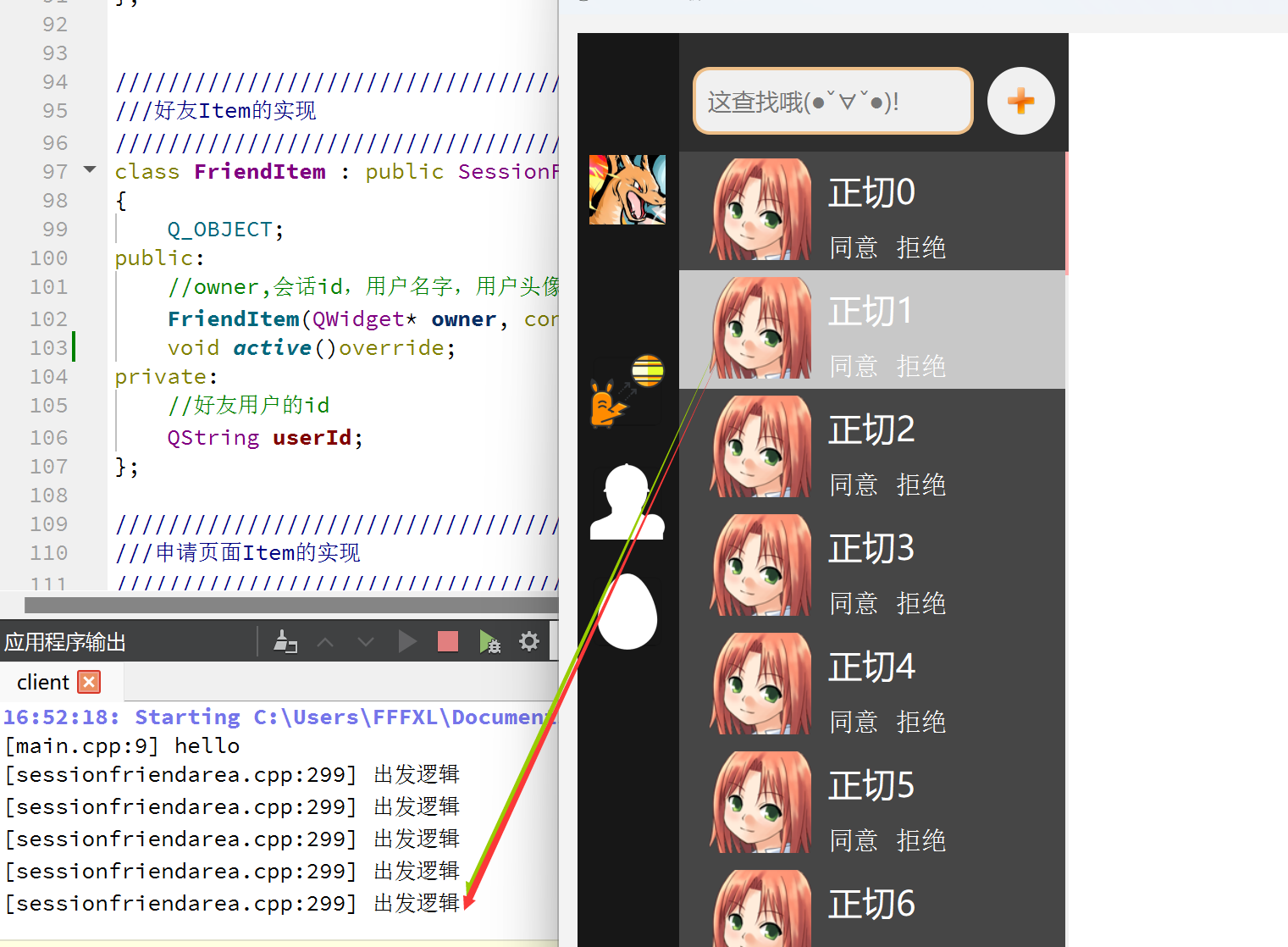
项目:微服务即时通讯系统客户端(基于C++QT)]四,中间界面搭建和逻辑准备
四,中间界面搭建 前言:当项目越来越复杂的时候,或许画草图是非常好的选择 一,初始化中间窗口initMidWindow void mainWidget::initMidWindow() {//使用网格布局进行管理QGridLayout* layout new QGridLayout();//距离上方 20px 的距离&…...

【C语言】指针详解(一)
个人主页 : zxctscl 如有转载请先通知 文章目录 1.内存与地址2.指针变量与地址2.1 取地址操作符&2.2 指针变量2.3 指针类型2.4 解引用操作符2.5 指针变量的大小 3. 指针变量类型的意义3.1 指针的解引用 4. const修饰指针4.1 const修饰变量4.2 const修饰指针变量…...

unity3D雨雪等粒子特效不穿透房屋效果实现(粒子不穿透模型)
做项目有时候会做天气模拟,模拟雨雪天气等等。但是容易忽略一个问题,就是房屋内不应该下雨或者下雪,这样不就穿帮了嘛。 下面就粒子穿透物体问题做一个demo。 正常下雨下雪在室内的话,你可以看到,粒子是穿透建筑的。 那要怎么模拟真实的雨雪天气,不让粒子穿透房屋建筑呢…...

ROS2安装cartographer
2. 安装Cartographer和Cartographer ROS 使用apt安装(推荐): bash sudo apt install ros-humble-cartographer-ros或者,从源代码安装: bash sudo apt-get update sudo apt-get install -y python3-wstool python3…...

kafka测试
1】确认 ZooKeeper 服务状态 为了进一步确认 ZooKeeper 服务的状态,你可以执行以下操作: 检查 ZooKeeper 服务状态: docker ps 确保 ZooKeeper 容器正在运行。 检查 ZooKeeper 日志: docker logs zookeeper 查看最新的日志条目&…...

总结C/C++中内存区域划分
目录 1.C/C程序内存分配主要的几个区域: 2.内存分布图 1.C/C程序内存分配主要的几个区域: 1、栈区 2、堆区 3、数据段(静态区) 4.代码段 2.内存分布图 如图: static修饰静态变量成员——放在静态区 int globalVar 是…...

第168天:应急响应-ELK 日志分析系统Yara规则样本识别特征提取规则编写
目录 案例一:ELK 搭建使用-导入文件&监控日志&语法筛选 案例二:Yara 规则使用-规则检测&分析特征&自写规则 案例一:ELK 搭建使用-导入文件&监控日志&语法筛选 该软件是专业分析日志的工具,但是不支持安…...

MySQL 面试题及答案
MySQL 面试题及答案: 一、基础问题 什么是数据库索引?有哪些类型? 答:数据库索引是一种数据结构,用于提高数据库查询的效率。它就像一本书的目录,可以快速定位到特定的数据行。 类型主要有: …...

vue仿chatGpt的AI聊天功能--大模型通义千问(阿里云)
vue仿chatGpt的AI聊天功能–大模型通义千问(阿里云) 通义千问是由阿里云自主研发的大语言模型,用于理解和分析用户输入的自然语言。 1. 创建API-KEY并配置环境变量 打开通义千问网站进行登录,登陆之后创建api-key,右…...

养老院管理系统(含源码+sql+视频导入教程+文档)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1 、功能描述 养老院管理系统拥有两种角色:管理员和护工 管理员:用户管理、老人信息管理、事故记录管理、入住费用管理、护工薪资管理、护工请假管理、床位管理、请假管理等 护…...

大数据的挑战是小文件
小文件可能会给存储平台及其支持的应用程序带来大问题。在 Google 上搜索 “small files performance” 会产生 2M 的结果。这篇博文将更深入地研究小文件问题,深入研究其根源并总结解决方案。 问题陈述 出于本讨论的目的,小文件通常被视为小于 64 KB …...

迁移学习案例-python代码
大白话 迁移学习就是用不太相同但又有一些联系的A和B数据,训练同一个网络。比如,先用A数据训练一下网络,然后再用B数据训练一下网络,那么就说最后的模型是从A迁移到B的。 迁移学习的具体形式是多种多样的,比如先用A训练…...

MCUboot 和 U-Boot区别
MCUboot 和 U-Boot 都是用于嵌入式系统的引导加载程序,但它们在一些方面存在区别: 功能特性 安全特性侧重不同 MCUboot :更专注于安全引导方面,强调安全启动、固件完整性验证和加密等安全功能。它提供了强大的安全机制来防止恶意…...

Apache OFBiz SSRF漏洞CVE-2024-45507分析
Apache OFBiz介绍 Apache OFBiz 是一个功能丰富的开源电子商务平台,包含完整的商业解决方案,适用于多种行业。它提供了一套全面的服务,包括客户关系管理(CRM)、企业资源规划(ERP)、订单管理、产…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

掌握 HTTP 请求:理解 cURL GET 语法
cURL 是一个强大的命令行工具,用于发送 HTTP 请求和与 Web 服务器交互。在 Web 开发和测试中,cURL 经常用于发送 GET 请求来获取服务器资源。本文将详细介绍 cURL GET 请求的语法和使用方法。 一、cURL 基本概念 cURL 是 "Client URL" 的缩写…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
