基于二分查找的动态规划 leetcode 300.最长递增子序列
如题:
https://leetcode.cn/problems/longest-increasing-subsequence/description/

其实常规动态规划的解法就没什么好说的了,有意思的是官方放出了一个二分查找的动态规化解法,时间复杂度能降到O(nlog(n)),但是为什么这样能解,似乎讲的不是那么清楚。
另外,即使是从操作步骤及状态转移函数上来说,可能俄罗斯套娃的第二个解里面还说的更清楚一点~~。具体可以去看题解:
. - 力扣(LeetCode). - 备战技术面试?力扣提供海量技术面试资源,帮助你高效提升编程技能,轻松拿下世界 IT 名企 Dream Offer。![]() https://leetcode.cn/problems/russian-doll-envelopes/solutions/633231/e-luo-si-tao-wa-xin-feng-wen-ti-by-leetc-wj68/注:因为俄罗斯套娃信封问题,最终转换成了最长递增子序列问题,所以在求最长递增子序列的时候的解法是一模一样的,下面的截图就是354.俄罗斯套娃信封问题的官方解二。
https://leetcode.cn/problems/russian-doll-envelopes/solutions/633231/e-luo-si-tao-wa-xin-feng-wen-ti-by-leetc-wj68/注:因为俄罗斯套娃信封问题,最终转换成了最长递增子序列问题,所以在求最长递增子序列的时候的解法是一模一样的,下面的截图就是354.俄罗斯套娃信封问题的官方解二。

这里面最关键的就是“f[j]表示h的前i个元素可以组成的长度为j的最长严格递增子序列的末尾元素的最小值”这一点,只要f[j]满足这一条件(状态转移的公式也完全是按照这个概念来的),并且把所有有定义的f[j]都计算完,那么最大的j就是最长严格递增子序列的长度(j从0开始,则长度就是最大的j加1啦)。
一。初步实操
不过这个概念似乎本身就有点绕啊,结合一下实际操作更容易理解,并且操作过程我稍微加点东西(参考的是laboladong的算法笔记里面的patience game纸牌游戏,不过他也没有说这么解为什么一定行)
数组就用题目里的,即nums=[0,3,1,6,2,2,7],f函数也可以当成一个列表,长度会一点点增长,元素值也可能会更新,一开始f是空的。
第1步,直接把nums第0个元素加到f中,即f[0]=0

此时的f[0]的含义就是当前长度为1的严格递增子序列的末尾元素的最小值就是0
第2步,取nums第1个元素,值为3,它明显比f[0]=0大,所以把它放到f[1]

此时的f[1]的含义就是当前长度为2的严格递增子序列的末尾元素的最小值就是3
其实f[j]的含义永远不会变啦,只是值可能会变,后不缀述。
第3步,取nums[2]=1,它比f[0]=0大,比f[1]=3小,所以更新f[1]的值为1。

我为什么把1写在3的下面,没有把3擦掉?后面自有妙用,并且这就是patience game纸牌游戏的玩法。
注意,我们更新的位置就是大于等于1的最小值。即f=[0, 3],找1的位置,自然就是3了。
此处直接多列举些情况:
a)f=[0, 3, 4],找1,找到的位置索引为1(从0开始),即f[1]=3
b)f=[0, 3, 4],找4,找到的位置索引为2,即f[2]=4
c)f=[0, 3, 4, 4]?,找4,找到的位置索引为2,即f[2]=4(最左边的4哦),但是,但是注意了!f其实不可能出现这种情况,正因为我们会在f=[0, 3, 4]找4的时候返回位置2,所以我们不会再新增一个4,只会用4更新4(你也可以认为啥也没变),所以更新完了仍然是f=[0, 3, 4]。我只是在此阐述一下严格的查找逻辑。
d)官方题解里面说先找到小于它的最大值f[j0],然后去更新f[j0+1],其实是一样的,正如c)中所说,f中不会有重复值。
第4步:

第5步:

第6步:

第7步:

好,结束了,f最终为[0, 1, 2, 7],所以最长严格递增子序列的长度就是4。(我说“所以”,只是按照题解的说明说的,并不是在敷衍啊。。。,我的解释还在后面)
另外,你确实也找不到更长的严格递增子序列啦,比如0 3 6 7,0 1 2 7都是4。
你可能会问,f最终为[0, 1, 2, 7],是不是代表[0, 1, 2, 7]就是最长严格递增子序列?那还真不一定
我立马就给你举个反例,比如nums=[0,3,1,6,7,2,2],最终画出来还是一样的图

得到的自然是一样的f=[0, 1, 2, 7],但是明显[0, 1, 2, 7]不是最长严格递增子序列,当然喽此时最长严格递增子序列长度仍然是4,只是这次的答案只有:[0, 3, 6, 7]
你可能会问,那是不是上图的第一行就一定是最长严格递增子序列?那仍然还真不一定
我再给你举一个反例,比如nums=[6,0,3,1,2,2,7],第1行的6 3 2 7明显不是,不过提前透露一下,判断它是不是的办法十分简单,那就是如果它不是,它就不是【狗头】。

别急,我说“如果它不是”的意思就是,直接判断它是不是一个严格递增序列,只要它是,那它就是最长严格递增子序列。那如果它真不是,那我仍然想知道谁是,咋办呢,办法也很简单,就是从右往左,从上往下,挨个找,找到的第一个比右侧小的值,就在严格递增序列之中

最后一列那选7肯定没错,第3列2也OK,第1列3不行,往下找,1行(不是1 hang, 是1 xing哦),就它了,第0列6不行,0行,就它了,所以0 1 2 7必然是最长严格递增子序列,并且最终你会发现,这么找的算法复杂度还很低,它就是O(n),原因很简单,上图中的所有元素就是原nums中的元素,一共就n个,顶多把每个遍历一遍。至于为什么这样找就能找出来,下面再详述。
二。进一步分析
先言归正传,为什么最长严格递增子序列的长度,就是f的最终长度呢?
继续研究一下刚才的实操过程,再贴一下,nums=[0,3,1,6,2,2,7]
比如第4步,

此时我们已经处理完的元素为0 3 1 6,这里面的最长严格递增子序列只有0 1 6或者0 3 6,注意上图6放的位置,6一定在第2列(从第0列开始算),3一定在第1列,0一定在第0列,其实还有一个1,它也一定在第1列。虽然这里只有nums的前4个元素,但只要把局部想明白了,后面所有的元素都是按照这个规则来堆的。
之前说到,怎样才能从上图的这堆数字中找出最长严格递增子序列,而不是只知道其长度呢?
为什么不能简单地根据从左往右的顺序来取?原因很简单,比如上图的1,他虽然处于第1列,6处于第2列,但这并不代表在nums中它一定在6的左边,我立马给你找个反例:
nums=[0, 3, 6, 1],堆出来的f图跟上图一模一样,可是在nums中1明显在6的右边。所以问题就是,f图中不能直接看出所有数字在nums中的先后顺序。
如果你能知道摆放这些数字的先后顺序,那你就确切地找出所有可能的最长严格递增子序列。
即,比如我记住了,先放0,其次放3,再次放1,最后放6,那自然0 3 6, 0 1 6都是ok的,当然实际上代码中不会记住这件事。但是有一件事我们是能确定的,那就是在放6之前,第0列,第1列都有人了!否则6也跑不到第2列来,其实串起来说就是,第1列中有一个元素x,它一定在6之前就放进来了,并且它比6小,第0列中有一个元素y,它一定在x之前就放进来了,并且它比x小。
你可能有几点疑惑:
a)为啥一定会有y<x<6?
正如上面所说,虽然我记不住f图的堆放顺序,但是它一定有这么个过程啊,所以y和x是客观存在的,只是你不能一眼看出它们是谁。
你要是没明白,我再废话几句,回忆一下摆放过程,6为什么放在第2列,因为它比第1列的某个元素x大(同时如果6这一列在6之上还有元素z的话,那6自然还满足,它小于等于z),这里的x就是1(虽然3也比6小,但实际6是跟1比较的),1为什么在第1列,因为它比第0列的某个元素y大,这里的y就是0。
b)你为啥说有一个元素y,有一个元素x,跟6在同一行的0和3不就是的吗?
正如你所问,第0行的元素,摆放顺序必然是0在3之前,3在6之前。但是,第0行的元素它未必是一个递增序列,比如[6, 0, 1, 3],其f图如下,很明显,6 1 3它不行,0 1 3它才行

等等,我问的是同一行,你说第0行?em....这个坑请见文章第四大点
c)你为啥要强调有这么一个顺序,并且y<x<6?
因为y,x,6它就是当前的最长的严格递增子序列啊!
别跟上图搞混啊,我把对应图再放一下

d)嗯,我能明白y x 6一定是一个严格递增子序列了,但我想不明白它为什么一定是最长的?
如果不能证明这一点,那我这帖子仍然是在敷衍。所以到了最关键的步骤了。
另外,我们再确认一下,你怀疑最长严格递增子序列长度>=3,起码3的下限我们是确定了!
现在让我们抛开杂念【狗头】,不要管y,x具体是什么,但是6它是具体的,因为它就是我们当前正在摆放的元素,如下图,现在的实际情况就是,我们按照摆放规则,6就是摆在了第2列(从0列开始),但是你怀疑存在某个以当前这个6结尾的严格递增子序列,它的长度大于3,也就是说存在一个z,它能插到6的前面。我们逐个分析有没有这种可能性。

(1)这个序列是y x z 6
z明显在x之后再往图上摆放,如果当时x这一列下面没东西,末端就是x,那么会因为z大于x,所以z放到第2列末端。如果x这一列下面还有东西,末端是xmin,那还是一样啊,z更是大于xmin了。
那问题是如果z放到了第2列,那再轮到放6的时候,它怎么可能仍然放在第2列?它只可能放到3列了
(2)同样的道理,y z x 6,z y x 6都是不行的,与上图矛盾。
(3)这个序列是y x 6 z
开玩笑,我们现在处理的当前元素是6,后面的还没处理到,一个个来。我们现在要确定的是因为当前元素摆在第2列(从0列开始),所以以当前元素结尾的最长严格递增子序列的长度就是3。
所以说,其实我们每往图上摆一个元素,它摆在哪一列,就说明了以这个元素结尾的最长严格递增子序列的长度,就是对应的列数(从0列开始算的话,自然要加1啦)
等我们把所有元素都摆完了,那么最大的列数,自然就是真正的最长严格递增子序列的长度了。
(4)这个序列是y x z1 z2,它是4,比y x 6长呢,并且z1,z2在nums中排在6之前
完全有可能,比如nums=[0,3,1,7,8,6],f图如下,6仍然在第3列,但是在摆放6的时候,当前最长严格递增子序列的长度就已经是4了,而不是3.

但是注意,我们并没有说错,正如第3点中所说,是以6结尾的最长严格递增子序列长度为3.
我为什么之前说的时候没有加上“以6结尾”这个前缀,我先把之前的图放一下

因为当时的这个图,一共就3列,并且当时还没有到强调这个前缀的时候。所以重点就是第3点中的那段红字,可以再回顾一下,它就是证明的关键了!
三。上代码
注,由于原题只需要计算长度,不需要找出序列,所以代码中其实跟题解的逻辑是一样的,即只更新f值,而不是把所有数字摆成牌堆。上述的牌堆只是为了理解原理。
from typing import Listimport bisectclass Solution:def lengthOfLIS(self, nums: List[int]) -> int:piles = [nums[0]]for i in range(1, len(nums)):if piles[-1] < nums[i]:piles.append(nums[i])find_index = Solution.bisect_left(piles, nums[i])# find_index = bisect.bisect_left(piles, nums[i])piles[find_index] = nums[i]return len(piles)@staticmethoddef bisect_left(a, x, l=0, h=-1):if h == -1:h = len(a)while l < h:mid = (l + h) // 2if x > a[mid]:l = mid + 1else: # elif x <= a[mid]# 这里为什么不是h = mid - 1,因为如果找不到x,则找大于x的最小值,即右边界我们可能是需要的# 为什么把x == a[mid]的分支也合到这里面?其实只是想跟bisect.bisect_left逻辑保持一致而已,即如果存在重复的x,则返回最左边的x# 实际上本题不可能有重复的x,完全可以在找到x后立马返回,能稍微快那么一点点h = midreturn lif __name__ == '__main__':nums = [0, 3, 1, 6, 2, 2, 7]print(Solution().lengthOfLIS(nums))四。那序列到底怎么找出来?
前面提过找的方法,再总结一下

从右往左找,第3列(从0列开始),就选第0行的7
第2列,第0行2小于7,OK,就它了
第1列,第0行3大于2,不行,第1行1小于2,OK,就它了
第0列,第0行6大于1,不行,第1行0小于1,OK,就它了(对,你可能发现了,虽然第1列取的1已经是第1行了,但是第0列仍然从第0行开始找
为什么这么找一定行呢?
我们换个例子,nums=[3,8,7,4,5,1]

很明显,3 4 5就是最长严格递增子序列,这是我们直接看nums得出的。但是在f图上,怎么才能确定4是在5之前的呢?正如我们之前所说,你既然想从f图中获取信息,那就请想象,5之前一定有一个x比5小,这是第一个已知条件。条件二是:8绝对在5之前,这是无疑的,因为它们在第0行。
可惜现在8比5大,假设紧接着8下面的那个元素z比5小,请问z是不是一定在5之前,答案是一定!

有图好分析,现在把z标出来,假设z比5小,但是z在nums中就是排在5之后,有没有可能?没可能!假设z真的排在5之后,那z下面的4也肯定排在5之后,那问题来了,5到底是因为谁而来到了第2列(从0列开始),兄弟你排错队了啊!所以如果z比5小,它绝对排在5之前。
当然喽,我们看z的时候发现它其实是7,它虽然排在5之前,但它不顶用啊,同理的逻辑继续往下找,找到的第1个小于5的元素,绝对排在5之前。
问题1:
你刚才说如果z比5小,则它一定在5之前。但你好像没说,如果z大于等于5的话,它也一定在5之前啊?
它当然还是在5之前啦,因为它下面绝对有一个比5小的new_z,就是那个4啦,4在5之前,那z还不在5之前?
问题2:
现在发现4在第2行了(从第0行开始),那处理第0列的时候,还是从第0行开始吗?
自然得从第0行开始,其实我刚留了一个坑没说明白,我说8一定在5之前,是因为它们都在第0行,注意,不是因为它们是同一行,而是第0行。0乃创世之初,从左到右遵循先创与后创,其它行则不然。所以我们只有确定第0行不行的时候,才能往下找。
具体到第0列就是,我们只有发现3大于等于4的时候,才能去找1。当然喽,3实际小于4,所以我们没证据表明1是行的。我们只有证据表明,3是行的。
相关文章:

基于二分查找的动态规划 leetcode 300.最长递增子序列
如题: https://leetcode.cn/problems/longest-increasing-subsequence/description/ 其实常规动态规划的解法就没什么好说的了,有意思的是官方放出了一个二分查找的动态规化解法,时间复杂度能降到O(nlog(n)),但是为什么这样能解&…...

Java8 IntStream流sum的Bug
做. - 力扣(LeetCode)的时候发现 IntStream流中的sum在相加的过程中会加到突破Int上限导致数据不对,需要装成LongStream流才能有正确的输出。 long sum Arrays.stream(milestones).asLongStream().sum(); 要这样子写,只把sum改…...

PCL 索引空间采样
目录 一、概述 1.1原理 1.2实现步骤 1.3应用场景 二、代码实现 2.1关键函数 2.1.1 索引空间采样 2.1.2 可视化原始点云和下采样后的点云 2.2完整代码 三、实现效果 PCL点云算法汇总及实战案例汇总的目录地址链接: PCL点云算法与项目实战案例汇总…...
PasteForm最佳CRUD实践,实际案例PasteTemplate详解之3000问(三)
作为“贴代码”力推的一个CRUD实践项目PasteTemplate,在对现有的3个项目进行实战后效果非常舒服!下面就针对PasteForm为啥我愿称为最佳CRUD做一些回答: 哪里可以下载这个PasteForm的项目案例 目前“贴代码”对外使用PasteForm的项目有"贴Builder(PasteSpide…...

【无标题】logistic映射
当Logistic映射中的控制参数 μ \mu μ 为负数时,系统的行为与正数 μ \mu μ 的情况截然不同。Logistic映射的一般形式是: x ( t 1 ) μ x ( t ) ( 1 − x ( t ) ) x(t1) \mu x(t) (1 - x(t)) x(t1)μx(t)(1−x(t))其中 x ( t ) x(t) x(t) 表示时…...

基于Node.js+Express+MySQL+VUE科研成果网站发布查看科研信息科研成果论文下载免费安装部署
目录 1.技术选型 2.功能设计 3.系统架构 4.开发流程 5.开发背景 6.开发目标 7.技术可行性 8.功能可行性 8.1功能图 8.2 界面设计 8.3 部分代码 构建一个基于Spring Boot、Java Web、J2EE、MySQL数据库以及Vue前后端分离的科研成果网站,可…...

提升C++代码质量的一些建议
文章目录 1. 命名清晰2. 简洁性3. 一致性4. 注释5. 避免复杂性6. 重构7. 测试8. 错误处理9. 文档10. 代码复用11. 性能优化12. 安全性- 代码规范推荐 C开发中,写出优雅且可维护的代码不仅能提升代码质量,还能提高团队协作效率和项目长期的可扩展性。以下…...

起重机防摇摆技术如何达标-武汉正向科技
武汉正向科技防摇摆控制器 主要技术参数 1、防摇摆精度: 0.4 2、行车到达目标位置偏差位置偏差: 25mm 3、通讯方式:PROFINET / PROFIBUS / RS232 / RS422 / RS485; 4、消除载荷的摇摆达 96% 以上; 5、技术先进…...

[大语言模型-论文精读] MoRAG - 基于多部分融合的检索增强型人体动作生成
MoRAG--Multi-Fusion Retrieval Augmented Generation for Human Motion KS Shashank, S Maheshwari, RK Sarvadevabhatla - arXiv preprint arXiv:2409.12140, 2024 MoRAG - 基于多部分融合的检索增强型人体动作生成 1. 目录 MoRAG--Multi-Fusion Retrieval Augmented Generat…...

解决端口被占用
当你被你的编译器提醒, 当前端口被占用, 但明明你的服务什么的都没有启用,这时有三种解决办法: 1 。 重启 。 重启解决80%的问题 2 。 修改你的端口号 。 3 。 去windows命令行中查看,端口占用情况 第一步 …...

【递归】7. leetcode 404 左叶子之和
1 题目描述 题目链接:左叶子之和 2 解答思路 递归分为三步,接下来就按照这三步来思考问题 第一步:挖掘出相同的子问题 (关系到具体函数头的设计) 第二步:只关心具体子问题做了什么 (关系…...

react+antdMobie实现消息通知页面样式
一、实现效果 二、代码 import React, { useEffect, useState } from react; import style from ./style/index.less; import { CapsuleTabs, Ellipsis, Empty, SearchBar, Tag } from antd-mobile; //消息通知页面 export default function Notification(props) {const [opti…...

Git 撤销一个已经push到远端仓库的commit
在 Git 中,撤销一个已经推送到远程仓库的改动有几种不同的方法,具体取决于你是否想要完全删除改动,还是只是恢复文件的某个状态。以下是常见的几种方法: git revert 撤销特定的commit git revert 是最安全的方法,因为…...

lambda表达式底层实现
一、lambda 代码 & 反编译 原始Java代码 假设我们有以下简单的Java程序,它使用Lambda表达式来遍历并打印一个字符串列表: import java.util.Arrays; import java.util.List;public class LambdaExample {public static void main(String[] args) {…...
鸿蒙NEXT开发-组件事件监听和状态管理(基于最新api12稳定版)
注意:博主有个鸿蒙专栏,里面从上到下有关于鸿蒙next的教学文档,大家感兴趣可以学习下 如果大家觉得博主文章写的好的话,可以点下关注,博主会一直更新鸿蒙next相关知识 专栏地址: https://blog.csdn.net/qq_56760790/…...

《More Effective C++》的学习
引用与指针 没有所谓的null reference reference一定需要代表某个对象,所以C要求reference必须有初值。 QString &s; 使用reference可能比使用pointer更高效。 因为reference一定是有效的,而指针可能为空(需要多加一个判断࿰…...

Leetcode面试经典150题-322.零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示…...

python17_len()函数
len()函数 A B "" C "hello world" D 18 E 18def len_test(s):try:# 尝试计算字符串的长度length len(s)return lengthexcept TypeError:# 如果不是字符串,则返回 None 或者提示错误return Noneif __name__ "__main__":# 单…...
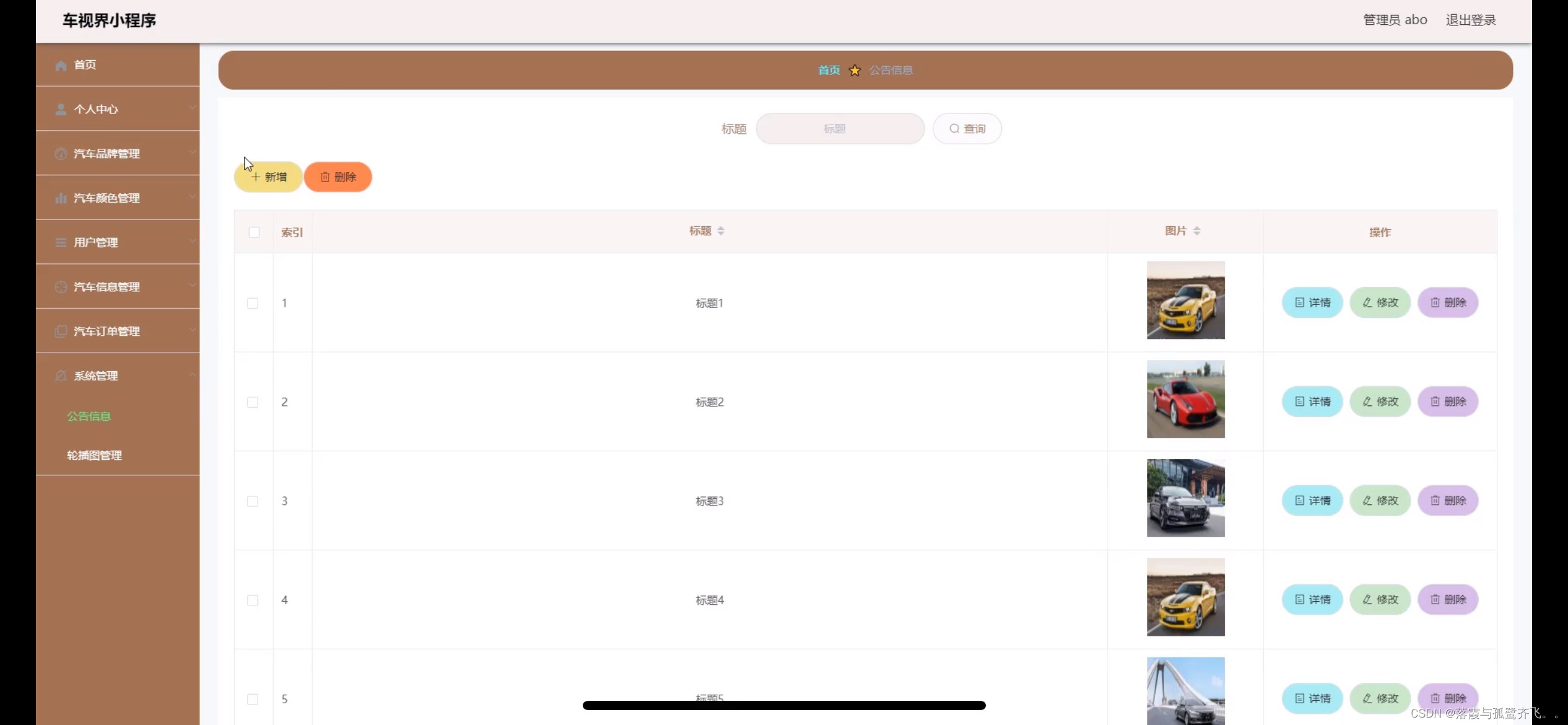
车视界系统小程序的设计
管理员账户功能包括:系统首页,个人中心,汽车品牌管理,汽车颜色管理,用户管理,汽车信息管理,汽车订单管理系统管理 微信端账号功能包括:系统首页,汽车信息,我…...

SQLCMD命令行工具导入数据并生成对应的日志文件
SQLCMD是一个命令行工具,专门用于在Microsoft SQL Server数据库上运行SQL脚本和管理任务。它提供了一种交互式和自动化的方式来执行SQL命令和脚本,并允许用户与SQL Server数据库进行高效的交互。以下是关于SQLCMD的详细介绍: 主要功能 执行SQL脚本: SQLCMD可以执行包含SQL…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
