数值计算的程序设计问题举例

### 数值计算的程序设计问题
#### 1. 结构静力分析计算
**涉及领域**:工程力学、建筑工程
**主要问题**:线性代数方程组(Linear Algebraic Equations)
**解释说明**:
在结构静力分析中,我们需要解决复杂的结构在外力作用下的响应,这通常会涉及到求解大量的线性代数方程组。具体来说,我们通过建立结构的刚度矩阵(Stiffness Matrix)和载荷向量(Load Vector),来计算节点位移(Node Displacement)和内部力(Internal Force)。
**举例说明**:
- **桥梁结构分析**:
- **问题**:当一座桥梁受到车辆荷载时,如何计算桥梁各节点的位移和应力分布?
- **解决方法**:建立桥梁的有限元模型,形成刚度矩阵和载荷向量,然后求解对应的线性代数方程组。
- **工具**:MATLAB、ANSYS等软件。
- **高层建筑抗震分析**:
- **问题**:高层建筑在地震作用下的位移和应力如何分布?
- **解决方法**:使用有限元法(Finite Element Method,FEM),求解结构的动态响应问题。
- **工具**:SAP2000、ETABS等软件。
### 数值计算的程序设计问题
#### 1. 结构静力分析计算
**涉及领域**:工程力学、建筑工程
**主要问题**:线性代数方程组(Linear Algebraic Equations)
**解释说明**:
在结构静力分析中,我们需要解决复杂的结构在外力作用下的响应,这通常会涉及到求解大量的线性代数方程组。具体步骤如下:
1. **建立结构模型**:
- 首先,需要建立结构的几何模型。这可以是桥梁、建筑物或其他工程结构。
- 使用有限元法(Finite Element Method, FEM)将结构离散化为有限数量的单元(Elements)和节点(Nodes)。
2. **定义材料和几何属性**:
- 为每个单元定义材料属性(如弹性模量、泊松比)和几何属性(如截面面积、惯性矩)。
3. **建立刚度矩阵(Stiffness Matrix, K)**:
- 刚度矩阵是一个描述结构刚度特性的矩阵。对于每一个单元,计算其局部刚度矩阵,然后通过坐标变换将其组装到全局刚度矩阵中。
4. **建立载荷向量(Load Vector, F)**:
- 根据外部加载条件(如集中力、分布力、温度变化等),建立载荷向量。
5. **应用边界条件**:
- 对结构施加边界条件(如固定支座、滑动支座),这会修改刚度矩阵和载荷向量。
6. **求解线性代数方程组**:
- 通过求解方程组 \( K \cdot U = F \),得到节点位移向量(Node Displacement Vector, U)。
- 利用节点位移,进一步计算内部力(Internal Force)和应力(Stress)。
**举例说明**:
- **桥梁结构分析**:
- **问题**:当一座桥梁受到车辆荷载时,如何计算桥梁各节点的位移和应力分布?
- **解决方法**:
1. **建立桥梁模型**:使用有限元法将桥梁离散化为多个单元和节点。
2. **定义材料和几何属性**:设置每个单元的材料属性(如钢材的弹性模量)和几何属性(如梁的截面面积)。
3. **建立刚度矩阵**:计算每个单元的局部刚度矩阵,并组装成全局刚度矩阵。
4. **建立载荷向量**:根据车辆的重量和位置,建立载荷向量。
5. **应用边界条件**:如桥梁两端的固定支座。
6. **求解方程组**:使用MATLAB或ANSYS求解 \( K \cdot U = F \),得到节点位移。
7. **计算内部力和应力**:根据节点位移计算各单元的内部力和应力分布。
- **工具**:MATLAB、ANSYS等软件。
**详细步骤**:
1. **建立桥梁模型**:
- 假设桥梁由多个梁单元组成,每个单元之间通过节点连接。
- 使用有限元软件(如ANSYS)或编程工具(如MATLAB)将桥梁模型离散化。
2. **定义材料和几何属性**:
- 设定钢材的弹性模量 \( E \) 和截面面积 \( A \)。
- 例如,钢材的弹性模量 \( E = 200 \times 10^9 \) Pa,截面面积 \( A = 0.01 \) m²。
3. **建立刚度矩阵**:
- 对于每个梁单元,计算局部刚度矩阵 \( k \):
\[
k = \frac{EA}{L} \begin{bmatrix}
1 & -1 \\
-1 & 1
\end{bmatrix}
\]
其中,\( L \) 是梁单元的长度。
4. **组装全局刚度矩阵**:
- 将各单元的局部刚度矩阵通过坐标变换组装到全局刚度矩阵 \( K \) 中。
5. **建立载荷向量**:
- 设定车辆荷载 \( P \),并将其作用在相应的节点上,形成载荷向量 \( F \)。
6. **应用边界条件**:
- 修改刚度矩阵和载荷向量,以反映支座的约束条件。
7. **求解方程组**:
- 使用数值方法(如高斯消去法、共轭梯度法)求解线性方程组 \( K \cdot U = F \),得到节点位移 \( U \)。
8. **计算内部力和应力**:
- 根据计算得到的节点位移,进一步求解每个单元的内部力和应力分布。
通过这些步骤,可以全面、准确地分析桥梁在车辆荷载作用下的静力响应。希望这些步骤能够帮助您更好地理解和应用结构静力分析的数值计算方法。如果有任何疑问,欢迎随时讨论。
好的,我们来详细逐步地进行桥梁结构分析的具体计算过程。假设我们分析的是一个简单的二维桥梁模型,由3个节点和2个梁单元组成。我们将使用MATLAB进行计算。
### 1. 建立桥梁模型
假设桥梁的节点和单元布置如下:
- 节点1:左支座(固定)
- 节点2:中间节点(自由)
- 节点3:右支座(固定)
- 单元1:连接节点1和节点2
- 单元2:连接节点2和节点3
假设每个单元的长度L=10m,截面面积A=0.01m²,弹性模量E=200GPa。
### 2. 定义材料和几何属性
```matlab
E = 200e9; % 弹性模量 (Pa)
A = 0.01; % 截面面积 (m²)
L = 10; % 单元长度 (m)
```
### 3. 计算局部刚度矩阵
对于每个单元,局部刚度矩阵为:
\[
k = \frac{EA}{L} \begin{bmatrix}
1 & -1 \\
-1 & 1
\end{bmatrix}
\]
```matlab
k = (E * A / L) * [1 -1; -1 1];
```
### 4. 组装全局刚度矩阵
全局刚度矩阵K的维度是节点数的2倍(因为每个节点有2个自由度:水平位移和竖直位移)。对于本例,我们忽略竖直方向的影响,只考虑水平位移,因此K是一个3x3的矩阵。
```matlab
K = zeros(3);
% 单元1的贡献
K(1:2, 1:2) = K(1:2, 1:2) + k;
% 单元2的贡献
K(2:3, 2:3) = K(2:3, 2:3) + k;
```
### 5. 建立载荷向量
假设在节点2施加一个水平向右的力P=1000N。
```matlab
F = [0; 1000; 0]; % 载荷向量
```
### 6. 应用边界条件
节点1和节点3是固定支座,需要将对应的自由度从方程组中移除。实际上,这意味着我们需要将K矩阵的对应行和列移除,将F向量的对应元素移除。
```matlab
K_reduced = K(2, 2); % 去掉固定支座的行和列
F_reduced = F(2); % 去掉固定支座的载荷
```
### 7. 求解线性代数方程组
对于简化后的系统,求解位移向量U。
```matlab
U_reduced = K_reduced \ F_reduced; % 求解位移
```
由于我们去掉了固定支座的自由度,U_reduced实际上就是节点2的位移。我们需要将其放回原位:
```matlab
U = [0; U_reduced; 0]; % 节点1和节点3的位移为0
```
### 8. 计算内部力和应力
根据节点位移,计算每个单元的内部力。对单元1和单元2分别进行计算。
```matlab
% 单元1的内部力
u1 = U(1:2);
F_internal1 = k * u1;
% 单元2的内部力
u2 = U(2:3);
F_internal2 = k * u2;
```
### 总结
通过上述步骤,我们完成了桥梁在车辆荷载作用下的静力分析。具体代码如下:
```matlab
% 1. 定义材料和几何属性
E = 200e9; % 弹性模量 (Pa)
A = 0.01; % 截面面积 (m²)
L = 10; % 单元长度 (m)
% 2. 计算局部刚度矩阵
k = (E * A / L) * [1 -1; -1 1];
% 3. 组装全局刚度矩阵
K = zeros(3);
K(1:2, 1:2) = K(1:2, 1:2) + k;
K(2:3, 2:3) = K(2:3, 2:3) + k;
% 4. 建立载荷向量
F = [0; 1000; 0];
% 5. 应用边界条件
K_reduced = K(2, 2);
F_reduced = F(2);
% 6. 求解线性代数方程组
U_reduced = K_reduced \ F_reduced;
% 7. 还原全局位移向量
U = [0; U_reduced; 0];
% 8. 计算内部力
u1 = U(1:2);
F_internal1 = k * u1;
u2 = U(2:3);
F_internal2 = k * u2;
% 显示结果
disp('节点位移:');
disp(U);
disp('单元1的内部力:');
disp(F_internal1);
disp('单元2的内部力:');
disp(F_internal2);
```
通过这种方式,我们可以分析桥梁在不同加载条件下的响应。希望这个详细的示例能帮助您更好地理解结构静力分析的具体实现方法。如果有任何进一步的问题,欢迎随时讨论!
相关文章:

数值计算的程序设计问题举例
### 数值计算的程序设计问题 #### 1. 结构静力分析计算 **涉及领域**:工程力学、建筑工程 **主要问题**:线性代数方程组(Linear Algebraic Equations) **解释说明**: 在结构静力分析中,我们需要解决复杂的…...

Java之方法的使用
修饰符 返回值 方法名称(形式参数){ } 当无参数的时候形式参数中什么都不写。 列如求两个数相加 修饰符可有可无。 方法重载: 1.方法名相同 2.参数列表不同 3。返回值不影响重载...

sudo 命令:掌握系统权限控制,实现安全高效管理
一、命令简介 sudo 命令允许系统管理员授权普通用户执行特定命令,并以管理员身份运行这些命令,通常需要输入用户自己的密码。 sudo 全称是"substitute user do",意为“替用户做”,也就是“以另一个用户的身…...

AndroidStudio导入so文件
点击app 右键依次选择New-Floder-JNI Floder 创建jni目录 将需要的so文件拷贝到jni目录 在app目录下,build.gradle文件的android{}中添加: sourceSets {main{jniLibs.srcDirs [src/main/jni]}}点击一下Sync Project with Gradle Files 然后编译生成AP…...

Kuebernetes 群集基于 Docker 部署
Kuebernetes 群集基于 Docker 部署 实验报告资源列表基础环境一、准备 Docker1、安装 Docker 二、安装 Kubeadm 工具1、配置 yum 源2、安装 Kubeadm 工具 三、初始化 Master 节点1、配置 Master 节点2、常见故障 四、Node 节点加入集群五、部署网络插件(CNI…...

追随 HarmonyOS NEXT,Solon v3.0 将在10月8日发布
Solon (开放原子开源基金会,孵化项目)原计划10月1日发布 v3.0 正式版。看到 HarmonyOS NEXT 将在 10月8日启用公测,现改为10月8日发布以示庆贺。另外,Solon 将在2025年启动“仓颉”版开发(届时,…...

服装时尚与动漫游戏的跨界联动:创新运营与策划策略研究
摘要:本论文聚焦于服装时尚与动漫游戏的跨界联动现象,深入探讨其在运营和策划方向的策略与实践。通过对相关理论的梳理和实际案例的分析,阐述了跨界联动的背景、意义、模式以及面临的挑战。研究发现,成功的跨界联动能够实现品牌价…...

Redis中String类型的常用命令(append,getrenge,setrange等命令)
Redis----String命令 前言.常见的String存储类型. 常见命令1. set 命令2. get 命令3. mget命令与mset命令4. setnx命令5. setex与psetex命令6. incr与incrby与incrbyfloat命令7. decr与decrby命令8. append命令9. getrange和setrange命令10. strlen命令. 前言. 常见的String存…...

深度拆解:如何在Facebook上做跨境电商?
国内社交媒体正在逐渐兴盛,海外也不例外。在数字营销的新时代,Facebook已成为跨境电商不可或缺的平台之一。通过Facebook的巨大流量,卖家可以更好的触及潜在消费者,以实现销售增长。本文就深度拆解一下,卖家如何利用Fb…...

为啥数据需转换成tensor才能参与后续建模训练
将数据转换为Tensor(张量)格式用于深度学习和机器学习模型训练,主要是出于以下几个关键原因: 数值计算的效率:Tensor(由PyTorch、TensorFlow等库提供)是在GPU上执行高效的数值运算的数据结构。相…...

leetcode:380. O(1) 时间插入、删除和获取随机元素
实现RandomizedSet 类: RandomizedSet() 初始化 RandomizedSet 对象bool insert(int val) 当元素 val 不存在时,向集合中插入该项,并返回 true ;否则,返回 false 。bool remove(int val) 当元素 val 存在时࿰…...

Linux集群部署RabbitMQ
目录 一、准备三台虚拟机,配置相同 1、所有主机都需要hosts文件解析 2、所有主机安装erLang和rabbitmq 3、修改配置文件 4、导入rabbitmq 的管理界面 5、查看节点状态 6、设置erlang运行节点 7、rabitmq2和rabbitmq3重启服务 8、查看各个节点状态 二、添加…...

01DSP学习-了解DSP外设-以逆变器控制为例
(由于是回忆自己简单的DSP学习过程,所以博客看起来有些没有章法,请见谅~) 上一篇博客介绍了学习DSP需要的软件和硬件准备,以及一个DSP的工程包含了哪些东西。我的学习方法是目的导向,即我需要用什么我就学什么,并没有…...

【ArcGIS Pro实操第三期】多模式道路网构建(Multi-model road network construction)原理及实操案例
ArcGIS Pro实操第三期:多模式道路网构建原理及实操案例 1 概述1.1 原理 2 GIS实操2.1 新建文件并导入数据2.2 创建网络数据集2.3 设置连接策略(Setting up connectivity policies)2.4 添加成本(Adding cost attributes)…...

深度学习基础及技巧
机器学习中的监督学习 监督学习是通过对数据进行分析,找到数据的表达模型,对新输入的数据套用该模型做决策 主要分为训练和预测两个阶段 训练阶段:根据原始数据进行特征提取,然后使用决策树、随机森林等模型算法分析数据之间的特…...

Unity 外描边简单实现(Shader Graph)
1:原理 将物体的模型空间的位置(也就是顶点数据)放大,作为一个单独的渲染通道单独渲染,这时候模型是已经发大过的,要想看到外描边的效果,需要将正面显示的东西给去掉,显示背面渲染的…...

text2sql方法:NatSQL和DIN-SQL
NatSQL NatSQL出自2021年9月的论文《Natural SQL: Making SQL Easier to Infer from Natural Language Specifications》(github),它是一种SQL 中间表征(SQL intermediate representation(IR))方法。 NatSQL作者认为Text2SQL的关键挑战是自然语言描述和其对应的SQ…...

【新闻转载】Storm-0501:勒索软件攻击扩展到混合云环境
icrosoft发出警告,勒索软件团伙Storm-0501近期调整了攻击策略,目前正将目标瞄准混合云环境,旨在全面破坏受害者的资产。 该威胁行为者自2021年首次露面,起初作为Sabbath勒索软件行动的分支。随后,他们开始分发来自Hive…...
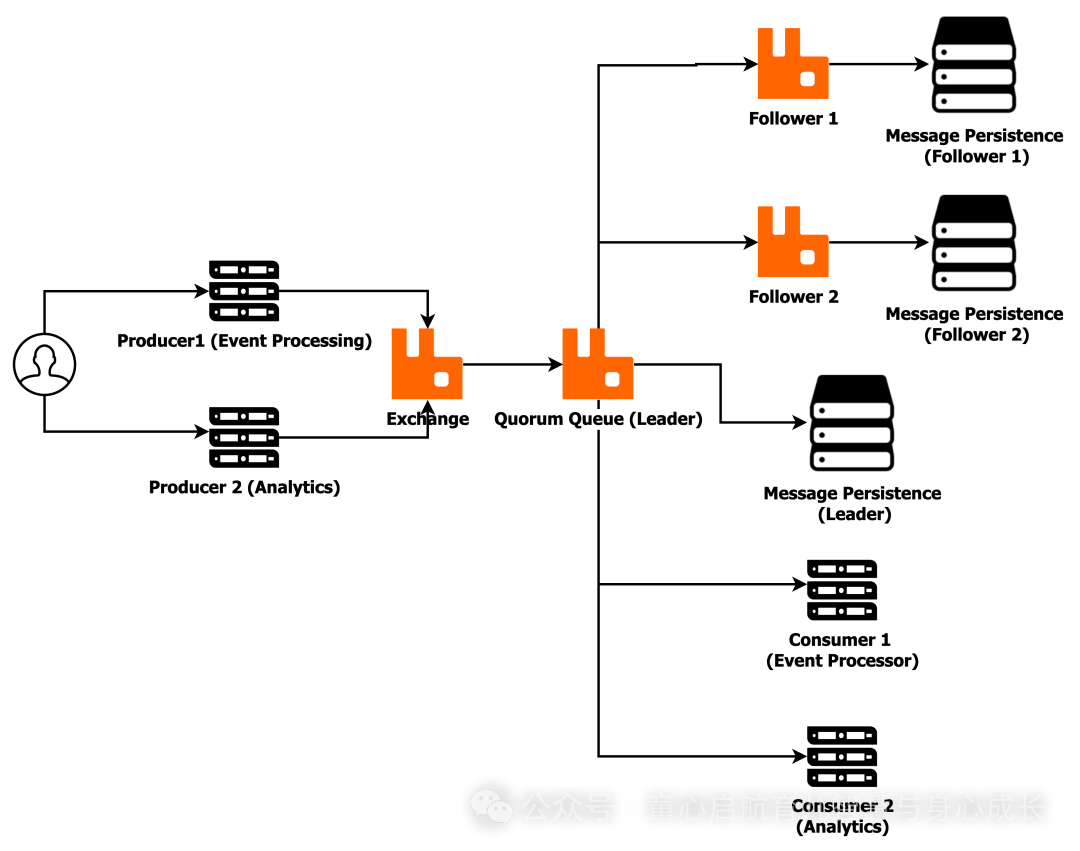
RabbitMQ 队列之战:Classic 和 Quorum 的性能洞察
RabbitMQ 是一个功能强大且广泛使用的消息代理,它通过处理消息的传输、存储和交付来促进分布式应用程序之间的通信。作为消息代理,RabbitMQ 充当生产者(发送消息的应用程序)和使用者(接收消息的应用程序)之…...

Spring Boot 集成 MySQL 的详细指南
在现代软件开发中,Spring Boot 因其简单易用而成为构建 Java 应用程序的热门选择。结合 MySQL这一常用关系型数据库,开发者可以快速构建出功能完善的后端服务。本文将详细介绍如何将 Spring Boot 与 MySQL 集成,提供从环境搭建到代码实现的全…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...
