奇异值分解(SVD)和图像压缩
在本文中,我将尝试解释 SVD 背后的数学及其几何意义,还有它在数据科学中的最常见的用法,图像压缩。

奇异值分解是一种常见的线性代数技术,可以将任意形状的矩阵分解成三个部分的乘积:U、S、V。原矩阵A可以表示为:

具体来说,A矩阵中的奇异值就是\Sigma矩阵中的对角线元素,它们是矩阵A的特征值的平方根,表示A矩阵在各个主方向上的拉伸程度。U矩阵是AAT的特征向量构成的正交矩阵,表示数据集在降维后的新的坐标系中的投影。V矩阵是ATA的特征向量构成的正交矩阵,表示每个数据点在降维后的新坐标系中的坐标。
一个矩阵的奇异值(singular values)是指其奇异值分解中的\Sigma矩阵的对角线上的元素,也就是特征值的平方根。换句话说,矩阵的奇异值是矩阵的奇异值分解中量度矩阵对输入矩阵进行的线性变换的尺度因子。
奇异值在很多应用中都有广泛的应用,例如在图像处理中,它可以用来对图像进行压缩和降噪;在推荐系统中,它可以用来对用户的偏好进行建模和推荐相关的产品或服务;在自然语言处理中,它可以用来对文本数据进行降维和特征提取等。
数学原理
如果我们有一个矩阵A
要计算 SVD,首先需要通过找到 AA^{T} 的特征值来计算奇异值。

上述矩阵的特征方程为:
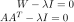
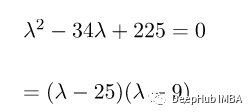
所以得到的奇异值是:
奇异向量就是 ATA 的正交特征向量集。ATA 的特征值是 25、9 和 0,由于 ATA 是对称的,我们知道特征向量是正交的。
所以,先计算 λ=25

然后进行化简:

其方向的单位向量为:

同理 对于 λ = 9,特征向量为:

对于第三个特征向量 0,我们可以使用它垂直于 v1 和 v2 的属性:

求解上述方程得到第三个特征向量
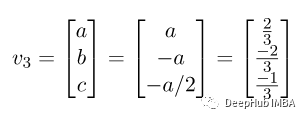
现在,我们计算 U,得到

这样就得到了最终的 SVD 方程:
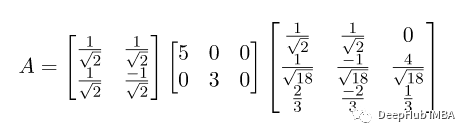
图像压缩
通过仅保留最重要的奇异值及其对应的奇异向量,SVD 被用于图像压缩以减小图像的大小。这可以从根本上减少在不丢失其最重要的视觉数据的情况下存储图像所需的额外存储量。
我们将使用下面的图像进行图像压缩:

导入库和读取图片十分简单
import requestsimport cv2import numpy as npimport matplotlib.pyplot as pltimg = cv2.imread('flower.bmp')gray_image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)gray_image = gray_image.astype(np.float64)
这里我们将图像转换成灰度图,执行奇异值分解
U, s, V = np.linalg.svd(gray_image, full_matrices=False)

numpy中就包含了该方法,所有我们直接调用即可,我们看看前 10 个奇异值
top_10_singular_values = s[:10]

可视化
plt.plot(range(1, len(s) + 1), s, 'r-')plt.xlabel("Rankings")plt.ylabel("Singular Values")plt.title("Singular Values versus their Rankings")plt.savefig("Singular_values_vs_rankings.png")plt.show()

从奇异值和排序图中可以注意到图像的大部分值都包含在少量奇异值中,所以可以得出到较高的奇异值包含的图像信息水平非常低,这也说明使用奇异值分解进行降维和图像压缩是可行的。
现在,让我们尝试重建和显示图像。
k_values = [10, 50, 100]plt.figure(figsize=(12,6))for i in range(len(k_values)):low_rank = U[:, :k_values[i]] @ np.diag(s[:k_values[i]]) @ V[:k_values[i], :]plt.subplot(2,3,i+1),plt.imshow(low_rank, cmap='gray'),plt.title(f"For K value = {k_values[i]}")plt.savefig("Reconstruction_with_k_values.png")

可以注意到具有不同 K 值的所有图像都有显着差异。使用了前 10 个奇异值,结果图像一点也不清晰。使用了前 50 个奇异值,生成的图像比之前的图像清晰多了,但是还有一些轻微的模糊。当我们使用前 100 个奇异值时,图像比前两张图像越来越清晰,基本和原图很接近了。随着 K 值的增加,图像的清晰度也会增加。
总结
本文介绍了奇异值分解 (SVD) 的数学原理和一个实际的应用案例,可以看到SVD是一种强大的图像压缩方法,有助于在减小图像尺寸的同时保留大部分重要的视觉信息。
https://avoid.overfit.cn/post/f0a675aad6994b61a2aa93fb647a0633
作者:Neokai
相关文章:

奇异值分解(SVD)和图像压缩
在本文中,我将尝试解释 SVD 背后的数学及其几何意义,还有它在数据科学中的最常见的用法,图像压缩。 奇异值分解是一种常见的线性代数技术,可以将任意形状的矩阵分解成三个部分的乘积:U、S、V。原矩阵A可以表示为&#…...

Java如何从yml文件获取对象
目录一、背景二、application.yml三、ChinaPersonFactory.java四、使用示例一、背景 在 SpringBoot 中,我们可以使用 Value 注解从属性文件(例如 application.yml 或 application.properties)中获取配置信息,但是只能获取简单的字…...
vue使用tinymce实现富文本编辑器
安装两个插件tinymce和 tinymce/tinymce-vue npm install tinymce5.10.3 tinymce/tinymce-vue5.0.0 -S 注意: tinymce/tinymce-vue 是对tinymce进行vue的包装,主要作用当作vue组件使用-S保存到package.json文件 2. 把node_modules/tinymce下的目录&a…...

yolov4实战训练数据
1、克隆项目文件 项目Github地址:https://github.com/AlexeyAB/darknet 打开终端,克隆项目 git clone https://github.com/AlexeyAB/darknet.git无法克隆的话,把https修改为git git clone git://github.com/AlexeyAB/darknet.git修改Makef…...

第十四章 DOM的Diff算法与key
React使用Diff算法来比较虚拟DOM树和真实DOM树之间的差异,并仅更新必要的部分,以提高性能。key的作用是在Diff算法中帮助React确定哪些节点已更改,哪些节点已添加或删除。 我们以案例来说明。 使用索引值和唯一ID作为key的效果 1、使用索引…...

MySQL调优
MySQL调优常见的回答如何回答效果更好业务层的优化如果只能用mysql该如何优化代码层的优化SQL层面优化总结常见的回答 SQL层面的优化——创建索引,创建联合索引,减少回表。再有就是少使用函数查询。 回表指的是数据库根据索引(非主键&#…...
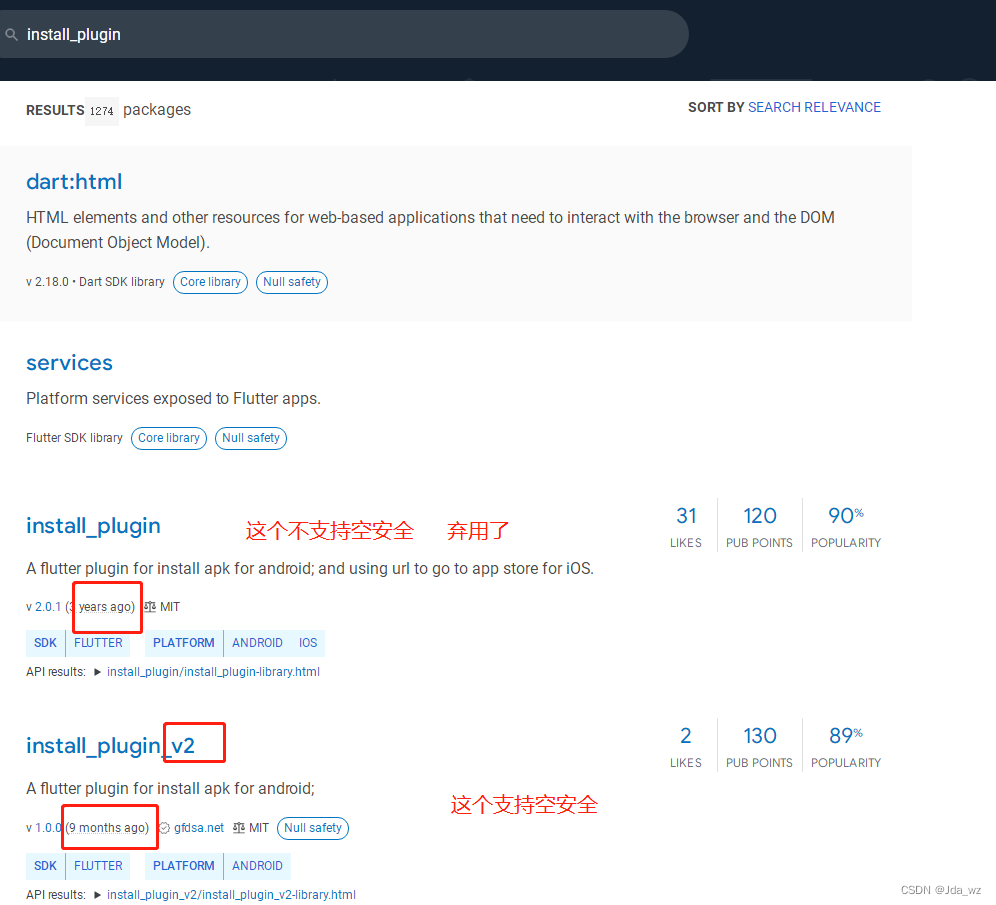
《Flutter进阶》flutter升级空安全遇到的一些问题及解决思路
空安全出来挺久了,由于业务需求较紧,一直没时间去升级空安全,最近花了几天去升级,发现其实升级也挺简单的,不要恐惧,没有想象中的多BUG。 flutter版本从1.22.4升到3.0.5; compileSdkVersion从1…...

最值得入手的五款骨传导耳机,几款高畅销的骨传导耳机
骨传导耳机是一种声音传导方式,主要通过颅骨、骨骼把声波传递到内耳,属于非入耳式的佩戴方式。相比传统入耳式耳机,骨传导耳机不会堵塞耳道,使用时可以开放双耳,不影响与他人的正常交流。骨传导耳机不会对耳朵产生任何…...
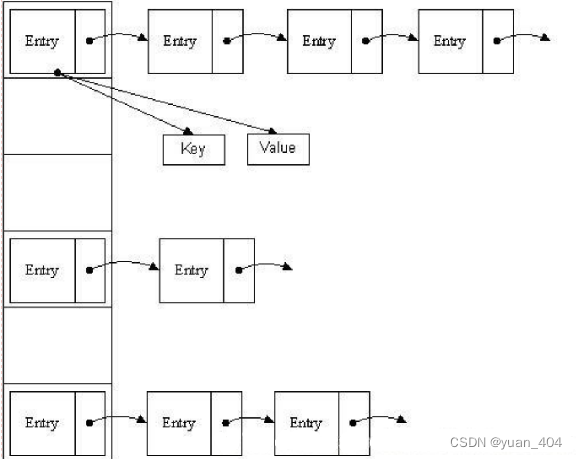
HashMap源码分析 (1.基础入门) 学习笔记
本章为 《HashMap全B站最细致源码分析课程》 拉钩教育HashMap 学习笔记 文章目录1. HashMap的数据结构1. 数组2. 链表3. 哈希表3.1 Hash1. HashMap的数据结构 数据结构中有数组和链表来实现对数据的存储,但这两者基本上是两个极端。 1. 数组 在生成数组的时候数…...

6 使用强制类型转换的注意事项
概述 在C语言中,强制类型转换是通过直接转换为特定类型的方式来实现的,类似于下面的代码。 float fNumber = 66.66f; // C语言的强制类型转换 int nData = (int)fNumber; 这种方式可以在任意两个类型间进行转换,太过随意和武断,很容易带来一些难以发现的隐患和问题。C++为…...

Leetcode.939 最小面积矩形
题目链接 Leetcode.939 最小面积矩形 Rating : 1752 题目描述 给定在 xy平面上的一组点,确定由这些点组成的矩形的最小面积,其中矩形的边平行于 x 轴和 y 轴。 如果没有任何矩形,就返回 0。 示例 1: 输入࿱…...
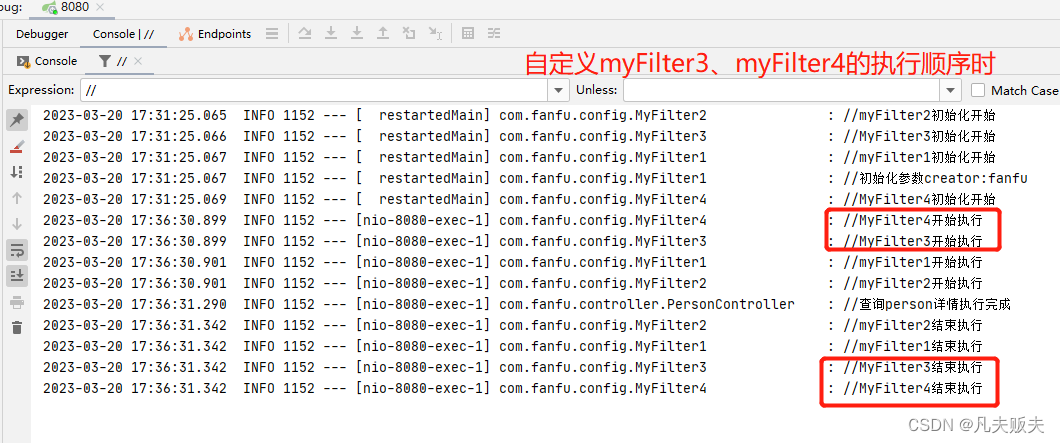
Springboot项目快速实现过滤器功能
前言很多时候,当你以为掌握了事实真相的时间,如果你能再深入一点,你可能会发现另外一些真相。比如面向切面编程的最佳编程实践是AOP,AOP的主要作用就是可以定义切入点,并在切入点纵向织入一些额外的统一操作࿰…...
基于springboot的简历系统的实现
摘 要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,简历系统当然也不能排除在外。简历系统是以实际运用为开发背景,运用软件工程原理和开发方法,采用…...

Vue3中watch的用法
watch函数用于侦听某个值的变化,当该值发生改变后,触发对应的处理逻辑。 一、watch的基本实例 <template><div><div>{{ count }}</div><button click"changCount">更改count的值</button></div> …...

MS python学习(18)
学习Pandas.DataFrame(2) load csv(comma seperated variable) files to DataFrame and vice versa upload csv files read/write csv files load data into jupyter notebook, create a new folder and then upload the csv files into it. (CSV comma seperated variable)…...

java笔记
前言 以下是一名java初学者在自学过程中所整理的笔记,欢迎大家浏览并留言,若有错误的地方请大家指正。 java语言特性 简单性:相对于其他编程语言而言,java较为简单,例如:java不再支持多继承,C…...

对象的构造及初始化
目录 一、如何初始化对象 二、构造方法 1.概念 2.特性 三、默认初始化 四、就地初始化 总结 一、如何初始化对象 在Java方法内部定义一个局部变量的时候,我们知道必须要进行初始化。 public class Test4 {public static void main(String[] args) {//未初始化…...

Socket 读取数据
1. Socket 配置参数中添加 1.1 读取 Socket 字节时的字节序 1.2 读取数据时,单次读取最大缓存值 1.3 从 Socket 读取数据时,遵从的数据包结构协议 1.4 服务器返回数据的最大值,防止客户端内存溢出 /*** Description: Socket 配置参数*/public…...
小白的Git入门教程(一)
这是本人的git的入门过程仅供参考 先是在官网下载git版本下载链接,安装步骤可以搜索其他大神的文章然后就是创建一个属于你的git本地库首先是创建一个文件夹作为根目录,这里我创建了一个叫test_git文件夹紧接着便进去新建文件夹,点击这里的g…...
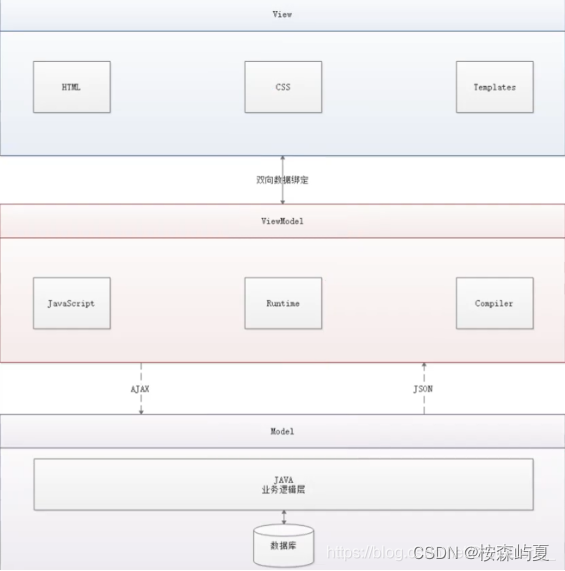
第一个Vue程序
第一个Vue程序 <body> <!--view层 变成了一个模板--> <div id"app">{{message}} </div><!--导入vue.js--> <script src"https://cdn.jsdelivr.net/npm/vue2.5.16/dist/vue.min.js"></script> <script>va…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
