排序输入的高效霍夫曼编码 | 贪心算法 3
前面我们讲到了 贪心算法的哈夫曼编码规则,原理图如下:
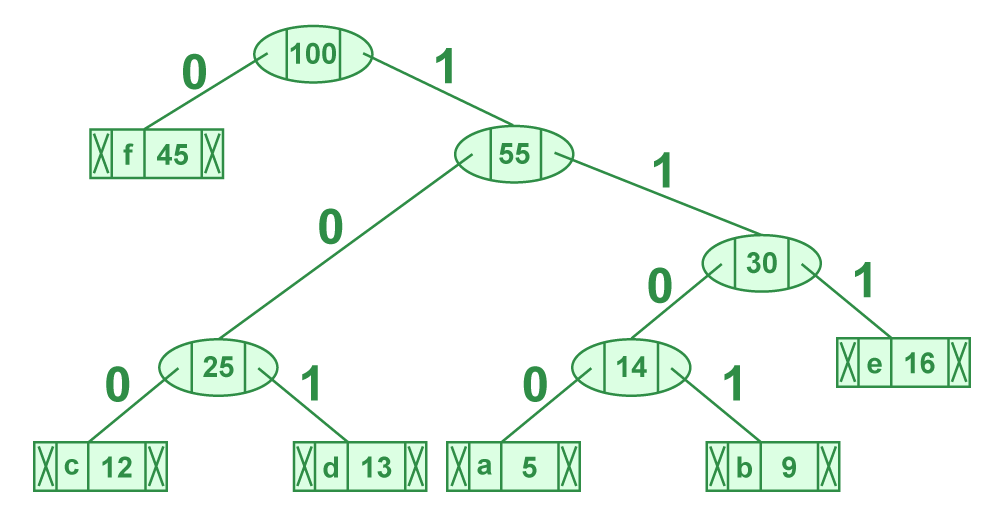
如果我们知道给定的数组已排序(按频率的非递减顺序),我们可以在 O(n) 时间内生成霍夫曼代码。以下是用于排序输入的 O(n) 算法。
1.创建两个空队列。
2.为每个唯一字符创建一个叶节点,并按频率非降序将其入队到第一个队列。最初第二个队列是空的。
3.通过检查两个队列的前端以最小频率使两个节点出队。重复以下步骤两次
1. 如果第二个队列为空,则从第一个队列中出队。
2. 如果第一个队列为空,则从第二个队列中出队。
3. 否则,比较两个队列的前端并将最小值出队。
4.创建一个新的内部节点,其频率等于两个节点频率的总和。将第一个 Dequeued 节点作为其左子节点,将第二个 Dequeued 节点作为右子节点。将此节点排入第二个队列。
5.当队列中有多个节点时,重复步骤#3 和#4。剩下的节点是根节点,树就完成了。
// C++ Program for Efficient Huffman Coding for Sorted input
#include <bits/stdc++.h>
using namespace std;// This constant can be avoided by explicitly
// calculating height of Huffman Tree
#define MAX_TREE_HT 100// A node of huffman tree
class QueueNode {
public:char data;unsigned freq;QueueNode *left, *right;
};// Structure for Queue: collection
// of Huffman Tree nodes (or QueueNodes)
class Queue {
public:int front, rear;int capacity;QueueNode** array;
};// A utility function to create a new Queuenode
QueueNode* newNode(char data, unsigned freq)
{QueueNode* temp = new QueueNode[(sizeof(QueueNode))];temp->left = temp->right = NULL;temp->data = data;temp->freq = freq;return temp;
}// A utility function to create a Queue of given capacity
Queue* createQueue(int capacity)
{Queue* queue = new Queue[(sizeof(Queue))];queue->front = queue->rear = -1;queue->capacity = capacity;queue->array = new QueueNode*[(queue->capacity* sizeof(QueueNode*))];return queue;
}// A utility function to check if size of given queue is 1
int isSizeOne(Queue* queue)
{return queue->front == queue->rear&& queue->front != -1;
}// A utility function to check if given queue is empty
int isEmpty(Queue* queue) { return queue->front == -1; }// A utility function to check if given queue is full
int isFull(Queue* queue)
{return queue->rear == queue->capacity - 1;
}// A utility function to add an item to queue
void enQueue(Queue* queue, QueueNode* item)
{if (isFull(queue))return;queue->array[++queue->rear] = item;if (queue->front == -1)++queue->front;
}// A utility function to remove an item from queue
QueueNode* deQueue(Queue* queue)
{if (isEmpty(queue))return NULL;QueueNode* temp = queue->array[queue->front];if (queue->front== queue->rear) // If there is only one item in queuequeue->front = queue->rear = -1;else++queue->front;return temp;
}// A utility function to get from of queue
QueueNode* getFront(Queue* queue)
{if (isEmpty(queue))return NULL;return queue->array[queue->front];
}/* A function to get minimum item from two queues */
QueueNode* findMin(Queue* firstQueue, Queue* secondQueue)
{// Step 3.a: If first queue is empty, dequeue from// second queueif (isEmpty(firstQueue))return deQueue(secondQueue);// Step 3.b: If second queue is empty, dequeue from// first queueif (isEmpty(secondQueue))return deQueue(firstQueue);// Step 3.c: Else, compare the front of two queues and// dequeue minimumif (getFront(firstQueue)->freq< getFront(secondQueue)->freq)return deQueue(firstQueue);return deQueue(secondQueue);
}// Utility function to check if this node is leaf
int isLeaf(QueueNode* root)
{return !(root->left) && !(root->right);
}// A utility function to print an array of size n
void printArr(int arr[], int n)
{int i;for (i = 0; i < n; ++i)cout << arr[i];cout << endl;
}// The main function that builds Huffman tree
QueueNode* buildHuffmanTree(char data[], int freq[],int size)
{QueueNode *left, *right, *top;// Step 1: Create two empty queuesQueue* firstQueue = createQueue(size);Queue* secondQueue = createQueue(size);// Step 2:Create a leaf node for each unique character// and Enqueue it to the first queue in non-decreasing// order of frequency. Initially second queue is emptyfor (int i = 0; i < size; ++i)enQueue(firstQueue, newNode(data[i], freq[i]));// Run while Queues contain more than one node. Finally,// first queue will be empty and second queue will// contain only one nodewhile (!(isEmpty(firstQueue) && isSizeOne(secondQueue))) {// Step 3: Dequeue two nodes with the minimum// frequency by examining the front of both queuesleft = findMin(firstQueue, secondQueue);right = findMin(firstQueue, secondQueue);// Step 4: Create a new internal node with frequency// equal to the sum of the two nodes frequencies.// Enqueue this node to second queue.top = newNode('$', left->freq + right->freq);top->left = left;top->right = right;enQueue(secondQueue, top);}return deQueue(secondQueue);
}// Prints huffman codes from the root of Huffman Tree. It
// uses arr[] to store codes
void printCodes(QueueNode* root, int arr[], int top)
{// Assign 0 to left edge and recurif (root->left) {arr[top] = 0;printCodes(root->left, arr, top + 1);}// Assign 1 to right edge and recurif (root->right) {arr[top] = 1;printCodes(root->right, arr, top + 1);}// If this is a leaf node, then it contains one of the// input characters, print the character and its code// from arr[]if (isLeaf(root)) {cout << root->data << ": ";printArr(arr, top);}
}// The main function that builds a Huffman Tree and print
// codes by traversing the built Huffman Tree
void HuffmanCodes(char data[], int freq[], int size)
{// Construct Huffman TreeQueueNode* root = buildHuffmanTree(data, freq, size);// Print Huffman codes using the Huffman tree built// aboveint arr[MAX_TREE_HT], top = 0;printCodes(root, arr, top);
}// Driver code
int main()
{char arr[] = { 'a', 'b', 'c', 'd', 'e', 'f' };int freq[] = { 5, 9, 12, 13, 16, 45 };int size = sizeof(arr) / sizeof(arr[0]);HuffmanCodes(arr, freq, size);return 0;
}// This code is contributed by rathbhupendra
Output:
f: 0 c: 100 d: 101 a: 1100 b: 1101 e: 111
QueueNode结构题代表哈夫曼的树结构
Queue的结构:集合霍夫曼树节点(或QueueNodes)
函数newNode:一个用于创建新Queuenode的实用函数
函数deQueue:从队列中删除项目的实用函数
函数HuffmanCodes:构建霍夫曼树并打印的主要函数代码通过遍历构建的霍夫曼树
函数printCodes:从霍夫曼树的根部打印霍夫曼代码。它使用arr[]存储代码
函数buildHuffmanTree:构建霍夫曼树的主要功能
- 步骤1:创建两个空队列
- 步骤2:为每个唯一的字符创建一个叶节点和在非递减队列中将它排到第一个队列频率的顺序。最初第二个队列为空。当队列包含多个节点时运行。最后,第一个队列为空,第二个队列为空只包含一个节点
- 步骤3:从队列中取出最小的两个节点通过检查两个队列的前面
- 步骤4:创建一个新的内部节点等于两个节点频率的和。将该节点加入第二个队列。
java代码实现如下:
// JavaScript program for the above approach// Class for the nodes of the Huffman tree
class QueueNode {
constructor(data = null, freq = null, left = null, right = null) {this.data = data;this.freq = freq;this.left = left;this.right = right;
}// Function to check if the following// node is a leaf node
isLeaf() {return (this.left == null && this.right == null);
}
}// Class for the two Queues
class Queue {
constructor() {this.queue = [];
}// Function for checking if the
// queue has only 1 node
isSizeOne() {return this.queue.length == 1;
}// Function for checking if
// the queue is empty
isEmpty() {return this.queue.length == 0;
}// Function to add item to the queue
enqueue(x) {this.queue.push(x);
}// Function to remove item from the queue
dequeue() {return this.queue.shift();
}
}// Function to get minimum item from two queues
function findMin(firstQueue, secondQueue) {// Step 3.1: If second queue is empty,
// dequeue from first queue
if (secondQueue.isEmpty()) {return firstQueue.dequeue();
}// Step 3.2: If first queue is empty,
// dequeue from second queue
if (firstQueue.isEmpty()) {return secondQueue.dequeue();
}// Step 3.3: Else, compare the front of
// two queues and dequeue minimum
if (firstQueue.queue[0].freq < secondQueue.queue[0].freq) {return firstQueue.dequeue();
}return secondQueue.dequeue();
}// The main function that builds Huffman tree
function buildHuffmanTree(data, freq, size) {
// Step 1: Create two empty queues
let firstQueue = new Queue();
let secondQueue = new Queue();// Step 2: Create a leaf node for each unique
// character and Enqueue it to the first queue
// in non-decreasing order of frequency.
// Initially second queue is empty.
for (let i = 0; i < size; i++) {firstQueue.enqueue(new QueueNode(data[i], freq[i]));
}// Run while Queues contain more than one node.
// Finally, first queue will be empty and
// second queue will contain only one node
while (!(firstQueue.isEmpty() && secondQueue.isSizeOne())) {// Step 3: Dequeue two nodes with the minimum// frequency by examining the front of both queueslet left = findMin(firstQueue, secondQueue);let right = findMin(firstQueue, secondQueue);// Step 4: Create a new internal node with// frequency equal to the sum of the two// nodes frequencies. Enqueue this node// to second queue.let top = new QueueNode("$", left.freq + right.freq, left, right);secondQueue.enqueue(top);
}return secondQueue.dequeue();
}// Prints huffman codes from the root of
// Huffman tree. It uses arr[] to store codes
function printCodes(root, arr) {// Assign 0 to left edge and recur
if (root.left) {arr.push(0);printCodes(root.left, arr);arr.pop();
}// Assign 1 to right edge and recur
if (root.right) {arr.push(1);printCodes(root.right, arr);arr.pop();
}// If this is a leaf node, then it contains
// one of the input characters, print the
// character and its code from arr[]
if (root.isLeaf()) {let output = root.data + ": ";for (let i = 0; i < arr.length; i++) {output += arr[i];}console.log(output);
}
}// The main function that builds a Huffman
// tree and print codes by traversing the
// built Huffman tree
function HuffmanCodes(data, freq, size) {// Construct Huffman Tree
let root = buildHuffmanTree(data, freq, size);// Print Huffman codes using the Huffman
// tree built above
let arr = [];
printCodes(root, arr);
}// Driver code
let arr = ["a", "b", "c", "d", "e", "f"];
let freq = [5, 9, 12, 13, 16, 45];
let size = arr.length;
HuffmanCodes(arr, freq, size);// This code is contributed by Prince Kumar
时间复杂度: O(n)
如果输入没有排序,需要先排序后才能被上面的算法处理。可以使用在 Theta(nlogn) 中运行的堆排序或合并排序来完成排序。因此,对于未排序的输入,整体时间复杂度变为 O(nlogn)。
辅助空间: O(n)
相关文章:

排序输入的高效霍夫曼编码 | 贪心算法 3
前面我们讲到了 贪心算法的哈夫曼编码规则,原理图如下: 如果我们知道给定的数组已排序(按频率的非递减顺序),我们可以在 O(n) 时间内生成霍夫曼代码。以下是用于排序输入的 O(n) 算法。1.创建两个空队列。2.为每个唯一…...

奇异值分解(SVD)和图像压缩
在本文中,我将尝试解释 SVD 背后的数学及其几何意义,还有它在数据科学中的最常见的用法,图像压缩。 奇异值分解是一种常见的线性代数技术,可以将任意形状的矩阵分解成三个部分的乘积:U、S、V。原矩阵A可以表示为&#…...

Java如何从yml文件获取对象
目录一、背景二、application.yml三、ChinaPersonFactory.java四、使用示例一、背景 在 SpringBoot 中,我们可以使用 Value 注解从属性文件(例如 application.yml 或 application.properties)中获取配置信息,但是只能获取简单的字…...
vue使用tinymce实现富文本编辑器
安装两个插件tinymce和 tinymce/tinymce-vue npm install tinymce5.10.3 tinymce/tinymce-vue5.0.0 -S 注意: tinymce/tinymce-vue 是对tinymce进行vue的包装,主要作用当作vue组件使用-S保存到package.json文件 2. 把node_modules/tinymce下的目录&a…...

yolov4实战训练数据
1、克隆项目文件 项目Github地址:https://github.com/AlexeyAB/darknet 打开终端,克隆项目 git clone https://github.com/AlexeyAB/darknet.git无法克隆的话,把https修改为git git clone git://github.com/AlexeyAB/darknet.git修改Makef…...

第十四章 DOM的Diff算法与key
React使用Diff算法来比较虚拟DOM树和真实DOM树之间的差异,并仅更新必要的部分,以提高性能。key的作用是在Diff算法中帮助React确定哪些节点已更改,哪些节点已添加或删除。 我们以案例来说明。 使用索引值和唯一ID作为key的效果 1、使用索引…...

MySQL调优
MySQL调优常见的回答如何回答效果更好业务层的优化如果只能用mysql该如何优化代码层的优化SQL层面优化总结常见的回答 SQL层面的优化——创建索引,创建联合索引,减少回表。再有就是少使用函数查询。 回表指的是数据库根据索引(非主键&#…...
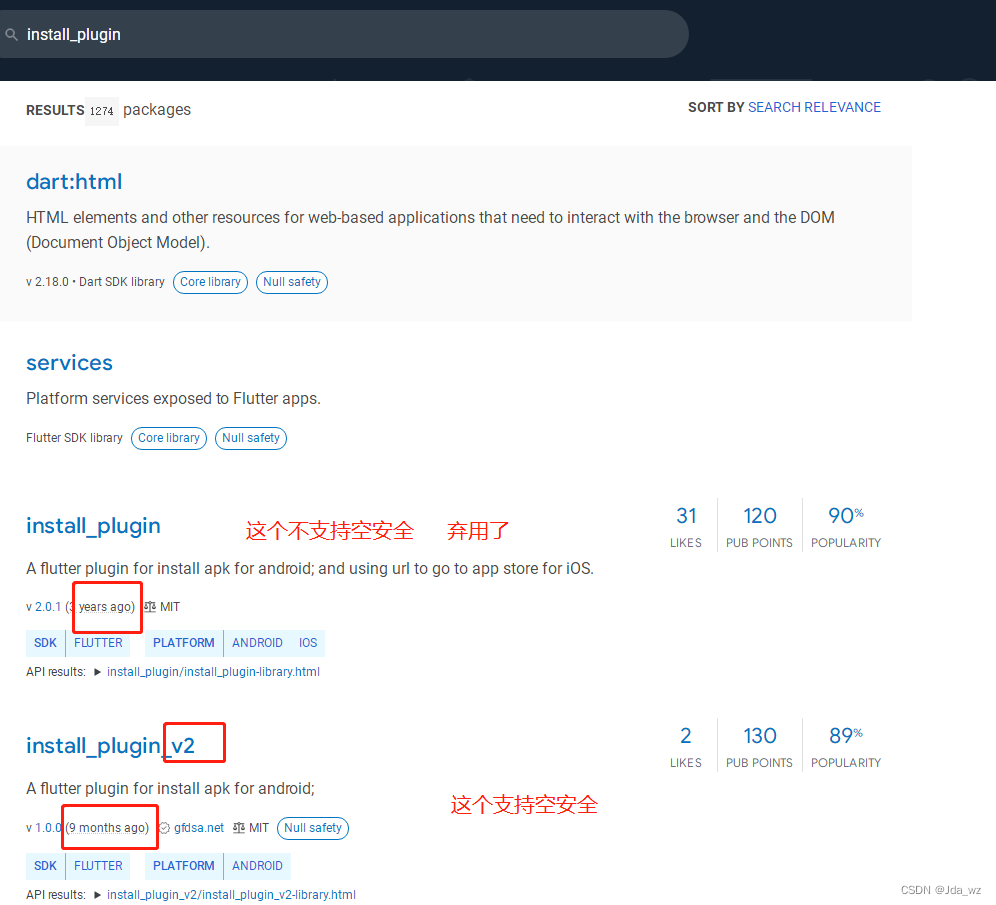
《Flutter进阶》flutter升级空安全遇到的一些问题及解决思路
空安全出来挺久了,由于业务需求较紧,一直没时间去升级空安全,最近花了几天去升级,发现其实升级也挺简单的,不要恐惧,没有想象中的多BUG。 flutter版本从1.22.4升到3.0.5; compileSdkVersion从1…...

最值得入手的五款骨传导耳机,几款高畅销的骨传导耳机
骨传导耳机是一种声音传导方式,主要通过颅骨、骨骼把声波传递到内耳,属于非入耳式的佩戴方式。相比传统入耳式耳机,骨传导耳机不会堵塞耳道,使用时可以开放双耳,不影响与他人的正常交流。骨传导耳机不会对耳朵产生任何…...
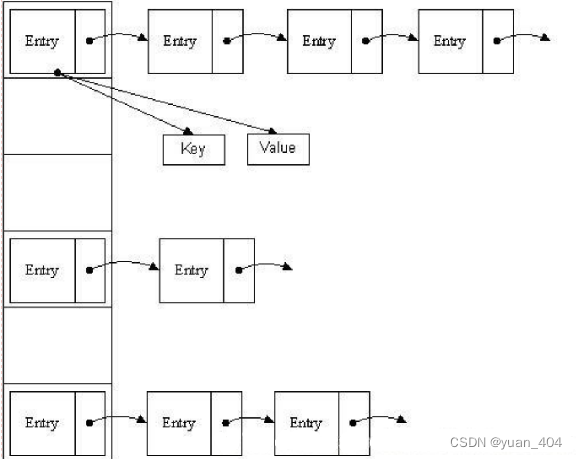
HashMap源码分析 (1.基础入门) 学习笔记
本章为 《HashMap全B站最细致源码分析课程》 拉钩教育HashMap 学习笔记 文章目录1. HashMap的数据结构1. 数组2. 链表3. 哈希表3.1 Hash1. HashMap的数据结构 数据结构中有数组和链表来实现对数据的存储,但这两者基本上是两个极端。 1. 数组 在生成数组的时候数…...

6 使用强制类型转换的注意事项
概述 在C语言中,强制类型转换是通过直接转换为特定类型的方式来实现的,类似于下面的代码。 float fNumber = 66.66f; // C语言的强制类型转换 int nData = (int)fNumber; 这种方式可以在任意两个类型间进行转换,太过随意和武断,很容易带来一些难以发现的隐患和问题。C++为…...

Leetcode.939 最小面积矩形
题目链接 Leetcode.939 最小面积矩形 Rating : 1752 题目描述 给定在 xy平面上的一组点,确定由这些点组成的矩形的最小面积,其中矩形的边平行于 x 轴和 y 轴。 如果没有任何矩形,就返回 0。 示例 1: 输入࿱…...
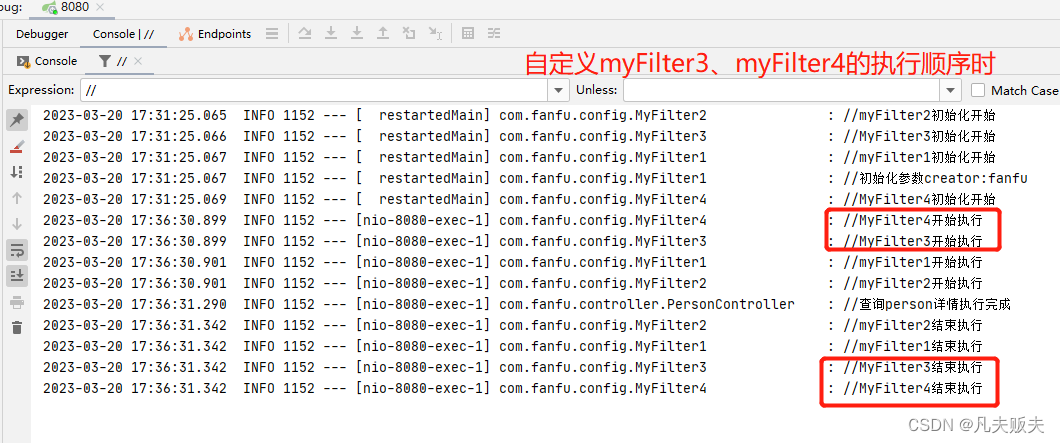
Springboot项目快速实现过滤器功能
前言很多时候,当你以为掌握了事实真相的时间,如果你能再深入一点,你可能会发现另外一些真相。比如面向切面编程的最佳编程实践是AOP,AOP的主要作用就是可以定义切入点,并在切入点纵向织入一些额外的统一操作࿰…...
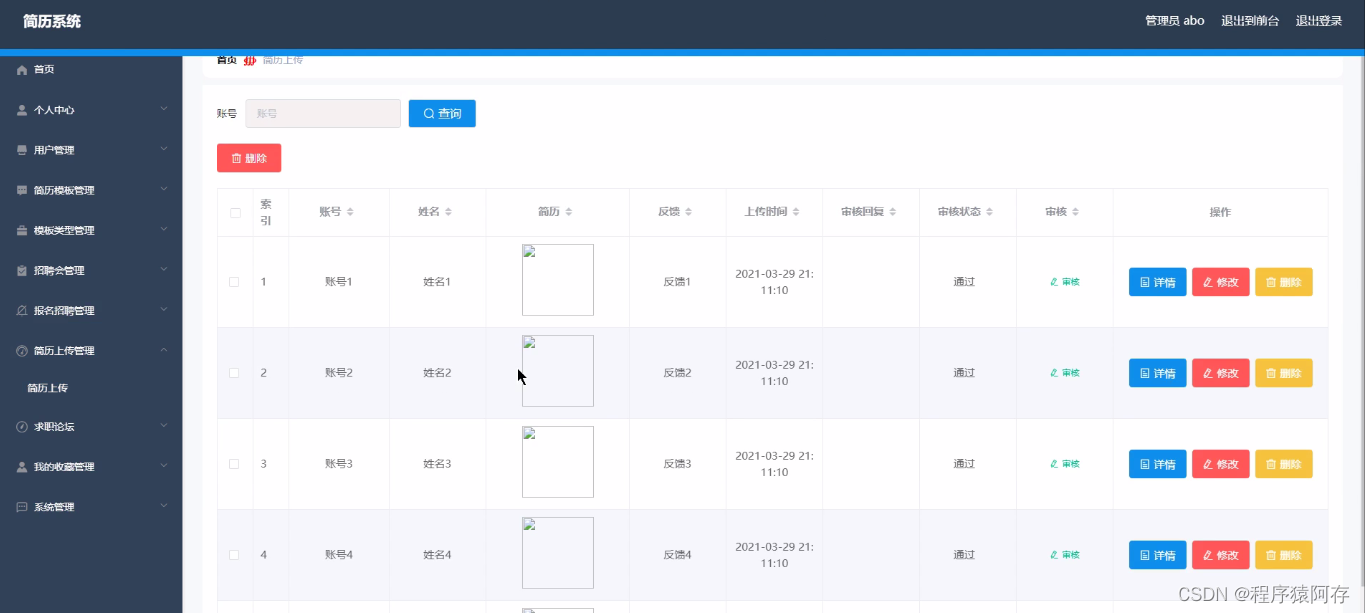
基于springboot的简历系统的实现
摘 要 随着科学技术的飞速发展,社会的方方面面、各行各业都在努力与现代的先进技术接轨,通过科技手段来提高自身的优势,简历系统当然也不能排除在外。简历系统是以实际运用为开发背景,运用软件工程原理和开发方法,采用…...

Vue3中watch的用法
watch函数用于侦听某个值的变化,当该值发生改变后,触发对应的处理逻辑。 一、watch的基本实例 <template><div><div>{{ count }}</div><button click"changCount">更改count的值</button></div> …...

MS python学习(18)
学习Pandas.DataFrame(2) load csv(comma seperated variable) files to DataFrame and vice versa upload csv files read/write csv files load data into jupyter notebook, create a new folder and then upload the csv files into it. (CSV comma seperated variable)…...

java笔记
前言 以下是一名java初学者在自学过程中所整理的笔记,欢迎大家浏览并留言,若有错误的地方请大家指正。 java语言特性 简单性:相对于其他编程语言而言,java较为简单,例如:java不再支持多继承,C…...

对象的构造及初始化
目录 一、如何初始化对象 二、构造方法 1.概念 2.特性 三、默认初始化 四、就地初始化 总结 一、如何初始化对象 在Java方法内部定义一个局部变量的时候,我们知道必须要进行初始化。 public class Test4 {public static void main(String[] args) {//未初始化…...

Socket 读取数据
1. Socket 配置参数中添加 1.1 读取 Socket 字节时的字节序 1.2 读取数据时,单次读取最大缓存值 1.3 从 Socket 读取数据时,遵从的数据包结构协议 1.4 服务器返回数据的最大值,防止客户端内存溢出 /*** Description: Socket 配置参数*/public…...
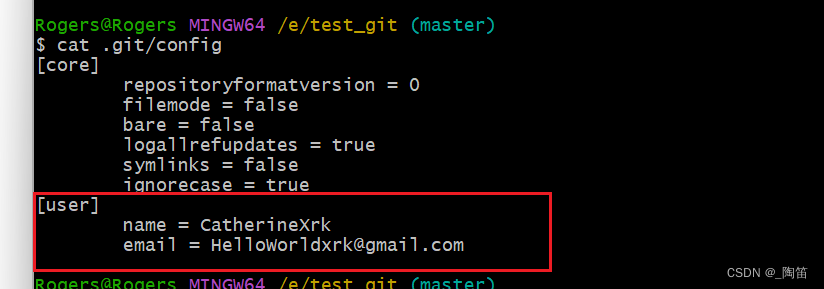
小白的Git入门教程(一)
这是本人的git的入门过程仅供参考 先是在官网下载git版本下载链接,安装步骤可以搜索其他大神的文章然后就是创建一个属于你的git本地库首先是创建一个文件夹作为根目录,这里我创建了一个叫test_git文件夹紧接着便进去新建文件夹,点击这里的g…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
