python 曲线平滑处理——方法总结(Savitzky-Golay 滤波器、make_interp_spline插值法和convolve滑动平均滤波)
文章目录
- 1 插值法对曲线平滑处理
- 1.1 插值法的常见实现方法
- 1.2 拟合和插值的区别
- 1.3 代码实例
- 2 Savitzky-Golay 滤波器实现曲线平滑
- 2.1 问题描述
- 2.2 Savitzky-Golay 滤波器--调用讲解
- 2.3 Savitzky-Golay 曲线平滑处理 示例
- 2.4 Savitzky-Golay原理剖析
- 3 基于Numpy.convolve实现滑动平均滤波
- 3.1 滑动平均概念
- 3.2 滑动平均的数学原理
- 3.3 语法
- 3.4 滑动平均滤波示例
有时我们得到曲线震荡或者噪声比较多,不利于观察曲线的趋势走向,需要对其平滑处理,
本文结介绍Savitzky-Golay 滤波器、make_interp_spline插值法和convolve滑动平均滤波,三种平滑处理方法
1 插值法对曲线平滑处理
实现所需的库: numpy、scipy、matplotlib
1.1 插值法的常见实现方法
nearest:最邻近插值法
zero:阶梯插值
slinear:线性插值
quadratic、cubic:2、3阶B样条曲线插值
1.2 拟合和插值的区别
1、插值:简单来说,插值就是根据原有数据进行填充,最后生成的曲线一定过原有点。
2拟合:拟合是通过原有数据,调整曲线系数,使得曲线与已知点集的差别(最小二乘)最小,最后生成的曲线不一定经过原有点。
1.3 代码实例
代码语法:
通过执行from scipy.interpolate import make_interp_spline,导入make_interp_spline模块,之后调用make_interp_spline(x, y)(x_smooth)函数实现。
官方帮助文档: scipy.interpolate.make_interp_spline
import numpy as np
from matplotlib import pyplot as plt
from scipy.interpolate import make_interp_splineSize = 30
x = np.arange(Size)
y = np.random.randint(1, Size, Size)#平滑前
plt.plot(x, y,'r')
plt.show()#平滑处理后
x_smooth = np.linspace(x.min(), x.max(), 500) # np.linspace 等差数列,从x.min()到x.max()生成300个数,便于后续插值
y_smooth = make_interp_spline(x, y)(x_smooth)
plt.plot(x_smooth, y_smooth,'b')
plt.show()
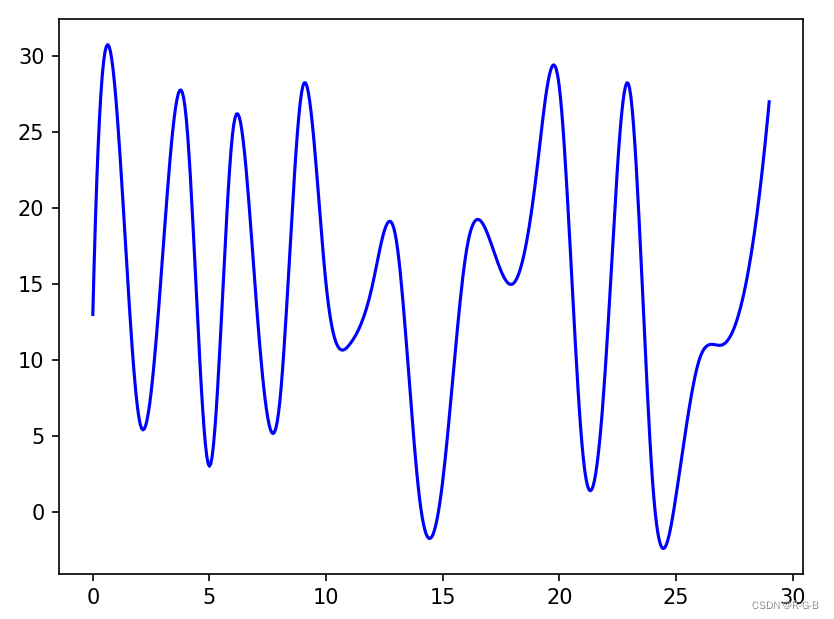
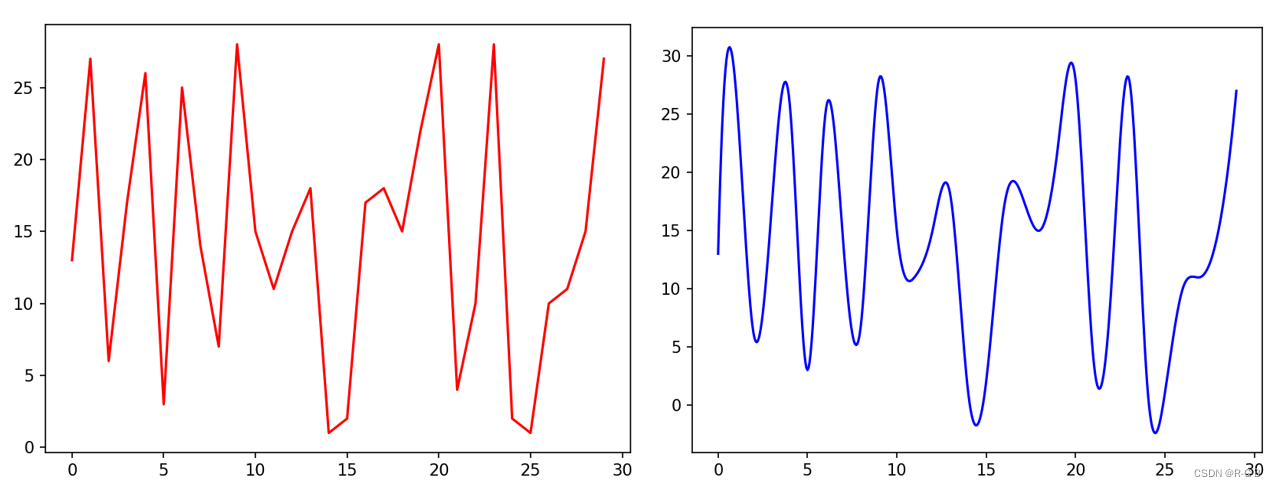
插值法 平滑处理 前后对比
2 Savitzky-Golay 滤波器实现曲线平滑
2.1 问题描述
在寻找曲线的波峰、波谷时,由于数据帧数多的原因,导致生成的曲线图噪声很大,不易寻找规律。如下图:
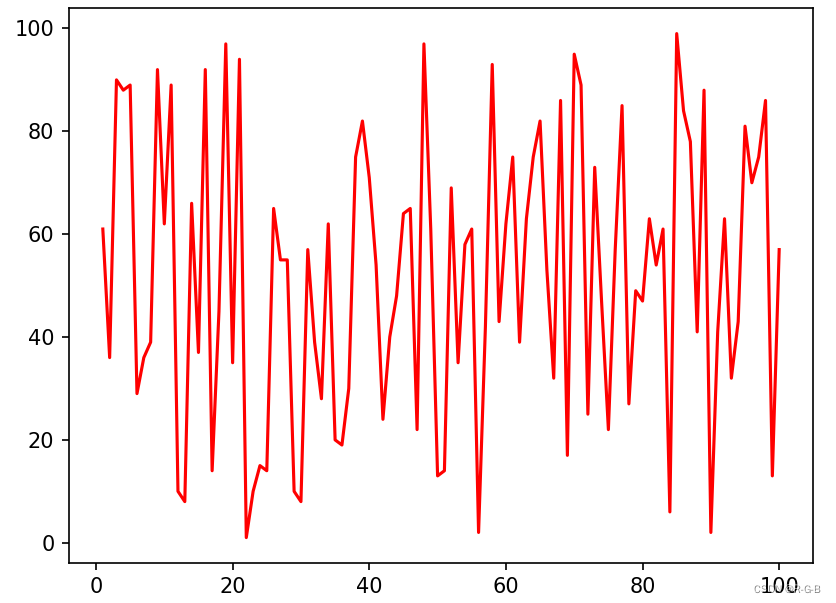
由于高频某些点的波动导致高频曲线非常难看,为了降低噪声干扰,需要对曲线做平滑处理,让曲线过渡更平滑。常见的对曲线进行平滑处理的方法包括: Savitzky-Golay 滤波器、插值法等。
2.2 Savitzky-Golay 滤波器–调用讲解
对曲线进行平滑处理,通过Savitzky-Golay 滤波器,可以在scipy库里直接调用,不需要再定义函数。
python中Savitzky-Golay滤波器调用如下:
y_smooth = scipy.signal.savgol_filter(y,53,3)
# 亦或
y_smooth2 = savgol_filter(y, 99, 1, mode= 'nearest')# 备注:
y:代表曲线点坐标(x,y)中的y值数组
window_length:窗口长度,该值需为正奇整数。例如:此处取值53
k值:polyorder为对窗口内的数据点进行k阶多项式拟合,k的值需要小于window_length。例如:此处取值3
mode:确定了要应用滤波器的填充信号的扩展类型。(This determines the type of extension to use for the padded signal to which the filter is applied. )调参规律:
现在看一下window_length和k这两个值对曲线的影响。
1)window_length对曲线的平滑作用:
( window_length的值越小,曲线越贴近真实曲线;window_length值越大,平滑效果越厉害(备注:该值必须为正奇整数)。
1)2)k值对曲线的平滑作用:
( k值越大,曲线越贴近真实曲线;k值越小,曲线平滑越厉害。另外,当k值较大时,受窗口长度限制,拟合会出现问题,高频曲线会变成直线。
2.3 Savitzky-Golay 曲线平滑处理 示例
# 用于生成问题描述中示例曲线的代码如下:
import numpy as np
from matplotlib import pyplot as pltSize = 100
x = np.linspace(1, Size,Size)#生成随机矩阵
data = np.random.randint(1, Size, Size)
print(data)# 可视化图线
plt.plot(x, data,'r')# 使用Savitzky-Golay 滤波器后得到平滑图线
from scipy.signal import savgol_filter
y = savgol_filter(data, 15, 2, mode= 'nearest')# 可视化图线
plt.plot(x, y, 'b', label = 'savgol')#显示曲线
plt.show()
#生成的随机矩阵
>>>
[61 36 90 88 89 29 36 39 92 62 89 10 8 66 37 92 14 45 97 35 94 1 10 1514 65 55 55 10 8 57 39 28 62 20 19 30 75 82 71 54 24 40 48 64 65 22 9761 13 14 69 35 58 61 2 42 93 43 62 75 39 63 75 82 53 32 86 17 95 89 2573 47 22 57 85 27 49 47 63 54 61 6 99 84 78 41 88 2 41 63 32 43 81 7075 86 13 57]
Savitzky-Golay 平滑曲线 效果
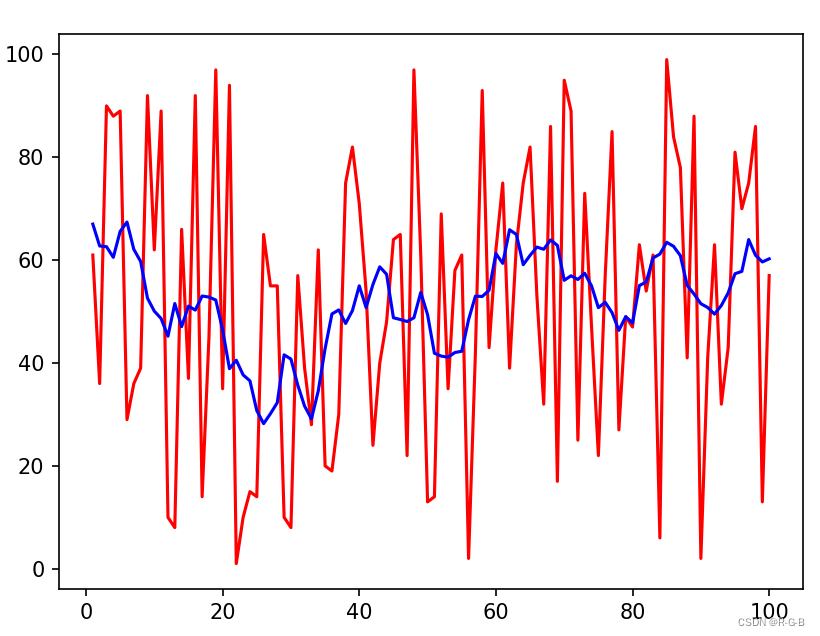
2.4 Savitzky-Golay原理剖析
在scipy官方帮助文档里可以看到关于Savitzky-Golay 滤波器中关于 savgol_filter()函数 的详细说明。
以下是关于 Savitzky-Golay平滑滤波 的简单介绍(参考Python 生成曲线进行快速平滑处理):
Savitzky-Golay平滑滤波是光谱预处理中的常用滤波方法,其 核心思想:是对一定长度窗口内的数据点进行k阶多项式拟合,从而得到拟合后的结果。 对它进行离散化处理后,S-G 滤波其实是一种移动窗口的加权平均算法,但是其加权系数不是简单的常数窗口,而是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出。
Savitzky-Golay平滑滤波被广泛地运用于数据流平滑除噪,是一种在时域内基于局域多项式最小二乘法拟合的滤波方法。这种滤波器的 最大特点:在滤除噪声的同时可以确保信号的形状、宽度不变。
使用平滑滤波器对信号滤波时,实际上是拟合了信号中的低频成分,而将高频成分平滑出去了。 如果噪声在高频端,那么滤波的结果就是去除了噪声,反之,若噪声在低频段,那么滤波的结果就是留下了噪声。
总之,平滑滤波是光谱分析中常用的预处理方法之一。用Savitzky-Golay方法进行平滑滤波,可以提高光谱的平滑性,并降低噪音的干扰。S-G平滑滤波的效果,随着选取窗宽不同而不同,可以满足多种不同场合的需求。
参考链接:Savitzky-Golay平滑滤波的python实现
3 基于Numpy.convolve实现滑动平均滤波
3.1 滑动平均概念
滑动平均滤波法 (又称:递推平均滤波法),它把连续取N个采样值看成一个队列 ,队列的长度固定为N ,每次采样到一个新数据放入队尾,并扔掉原来队首的一次数据(先进先出原则) 。把队列中的N个数据进行算术平均运算,就可获得新的滤波结果。
N值的选取:流量,N=12;压力:N=4;液面,N=4 ~ 12;温度,N=1~4
滑动平均的优缺点:
优点: 对周期性干扰有良好的抑制作用,平滑度高,适用于高频振荡的系统。
缺点: 灵敏度低,对偶然出现的脉冲性干扰的抑制作用较差,不易消除由于脉冲干扰所引起的采样值偏差,不适用于脉冲干扰比较严重的场合,比较浪费RAM 。
3.2 滑动平均的数学原理
滑动平均滤波法计算类似一维卷积的工作原理,滑动平均的N就对应一维卷积核大小(长度)。 区别在于:
(1)步长会有些区别,滑动平均滤波法滑动步长为1,而一维卷积步长可以自定义;
(2)一维卷积的核参数是需要更新迭代的,而滑动平均滤波法核参数都是1。
我们应该怎么利用这个相似性呢?其实也很简单,只需要把一维卷积核大小(长度)和N相等,步长设置为1,核参数都初始为1就可以了。由于一维卷积计算速度快,因此我们可以使用一维卷积来快速高效地实现这个功能。
滑动平均值是卷积数学运算的一个例子。对于滑动平均值,沿着输入滑动窗口并计算窗口内容的平均值。对于离散的1D信号,卷积是相同的,除了代替计算任意线性组合的平均值,即将每个元素乘以相应的系数并将结果相加。那些系数,一个用于窗口中的每个位置,有时称为卷积核。现在,N值的算术平均值是( x1 + x2 + . . . + xN ) / N ,所以相应的内核是( 1/N , 1/N , . . . , 1 / N ) ,这正是我们通过使用得到的np.ones((N,))/N。
3.3 语法
通过Numpy库中的convolve()函数可以实现这些功能。
def np_move_avg(a,n,mode="same"):return(np.convolve(a, np.ones((n,))/n, mode=mode))
Numpy.convolve函数:(numpy.convolve函数官方文档)
参数说明:
- a:(N,)输入的第一个一维数组
- v:(M,)输入的第二个一维数组
- mode:{‘full’, ‘valid’, ‘same’}参数可选,该参数指定np.convolve函数如何处理边缘。
mode可能的三种取值情况:
full’ 默认值,返回每一个卷积值,长度是N+M-1,在卷积的边缘处,信号不重叠,存在边际效应。
‘same’ 返回的数组长度为max(M, N),边际效应依旧存在。
‘valid’ 返回的数组长度为max(M,N)-min(M,N)+1,此时返回的是完全重叠的点。边缘的点无效。
和一维卷积参数类似,a就是被卷积数据,v是卷积核大小。
3.4 滑动平均滤波示例
np.convolve函数中通过mode参数指定如何处理边缘。
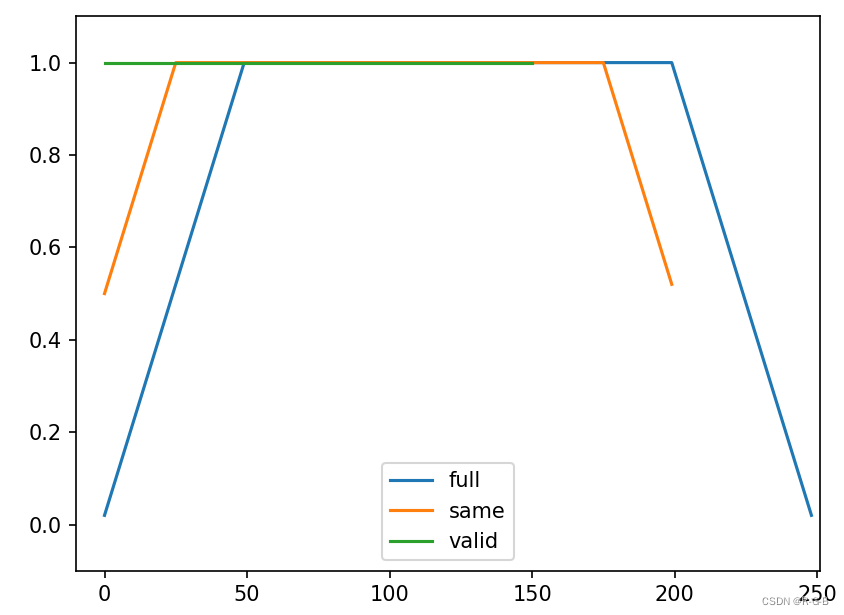
下面是一个说明模式不同取值之间差异的图:
import numpy as np
import matplotlib.pyplot as pltdef np_move_avg(a,n,mode="same"):return(np.convolve(a, np.ones((n,))/n, mode=mode))modes = ['full', 'same', 'valid']for m in modes:plt.plot(np_move_avg(np.ones((200,)), 50, mode=m))plt.axis([-10, 251, -.1, 1.1])plt.legend(modes, loc='lower center')plt.show()
参考链接:
[开发技巧]·Python极简实现滑动平均滤波(基于Numpy.convolve)
numpy中的convolve的理解
典型范例:
# 实现数据可视化中的数据平滑
import numpy as np
import matplotlib.pylab as plt'''
其它的一些知识点:
raise:当程序发生错误,python将自动引发异常,也可以通过raise显示的引发异常
一旦执行了raise语句,raise语句后面的语句将不能执行
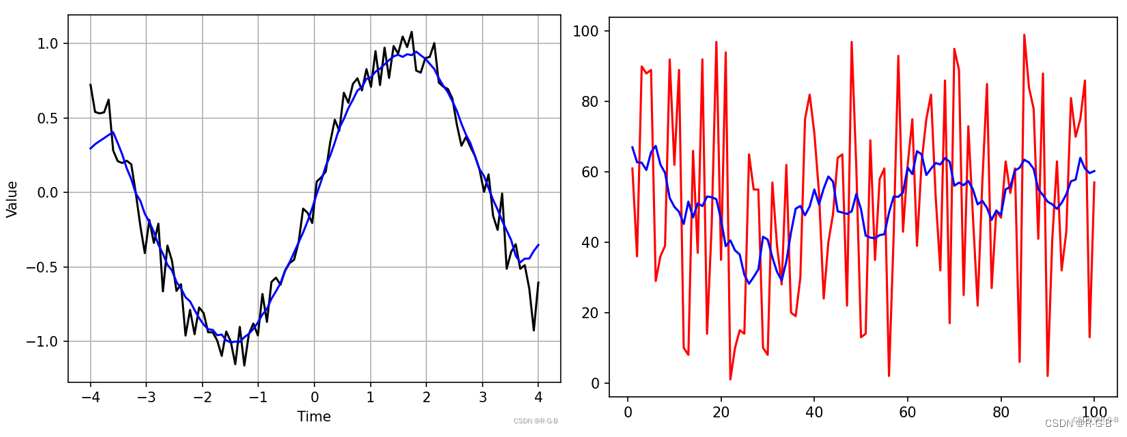
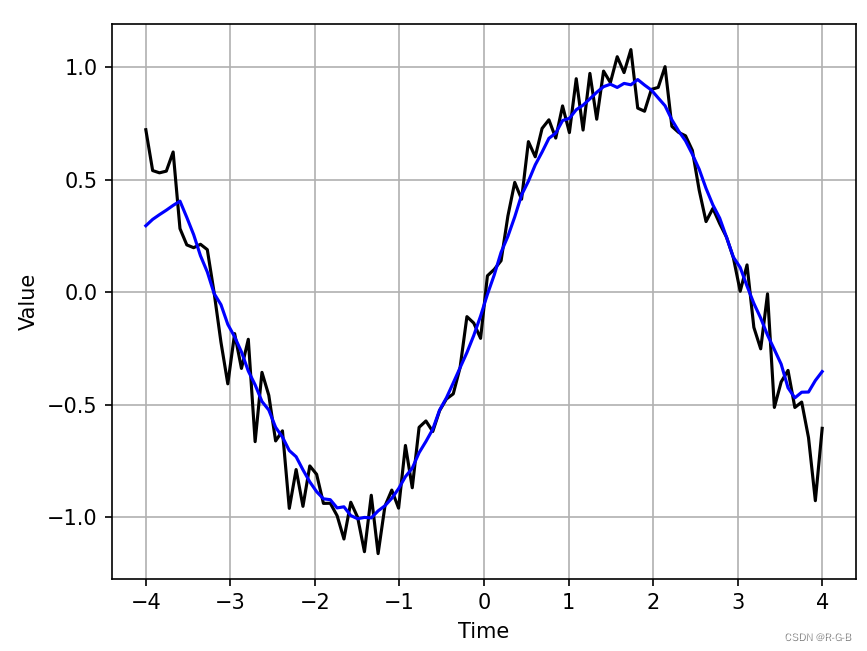
'''def moving_average(interval, windowsize):window = np.ones(int(windowsize)) / float(windowsize)re = np.convolve(interval, window, 'same')return redef LabberRing():t = np.linspace(-4, 4, 100) # np.linspace 等差数列,从-4到4生成100个数print('t=', t)# np.random.randn 标准正态分布的随机数,np.random.rand 随机样本数值y = np.sin(t) + np.random.randn(len(t)) * 0.1 # 标准正态分布中返回1个,或者多个样本值print('y=', y)plt.plot(t, y, 'k') # plot(横坐标,纵坐标, 颜色)y_av = moving_average(y, 10)plt.plot(t, y_av, 'b')plt.xlabel('Time')plt.ylabel('Value')# plt.grid()网格线设置plt.grid(True)plt.show()returnLabberRing() # 调用函数
相关文章:

python 曲线平滑处理——方法总结(Savitzky-Golay 滤波器、make_interp_spline插值法和convolve滑动平均滤波)
文章目录1 插值法对曲线平滑处理1.1 插值法的常见实现方法1.2 拟合和插值的区别1.3 代码实例2 Savitzky-Golay 滤波器实现曲线平滑2.1 问题描述2.2 Savitzky-Golay 滤波器--调用讲解2.3 Savitzky-Golay 曲线平滑处理 示例2.4 Savitzky-Golay原理剖析3 基于Numpy.convolve实现滑…...

小驰私房菜_10_camx Otp Dump
#小驰私房菜# #camx# #Otp Dump# 本篇文章分下面几点展开: 1、otp dump的目的? 2、如何打开otp dump开关? 3、otp guide手册如何查看? 4、如何初步确认dump 出来的数据是否正确? 一、otp dump的目的 关于otp的一些概念,这里就不做过多的介绍了,不了解的同学,可以先去…...

priority_queue(堆)干货归纳+用法示例
10.priority_queue一.priority_queue(堆Heap)简介1.堆的特点:2.使用场景:二.成员函数1.构造函数:priority_queue构造函数方式:2.push()函数:向priority_queue中插入一个元素:3.pop()…...

miniprogram-to-uniapp使用指南(各种小程序项目转换为uni-app项目)
小程序分类:uni-app qq小程序 支付宝小程序 百度小程序 钉钉小程序 微信小程序 小程序转成uni_app 小程序转为uni_app 小程序转uni_app 小程序转换 工具现在支持npm全局库、HBuilderX插件两种方式使用,任君选择,HBuilderX插件地址:…...

BZOJ2720: [Violet 5]列队春游 【概率与期望】
题意自行理解,先讲一下概率和期望怎么算 概率 概率准确的定义自行百度,这里就不赘述了 概率的计算其实很简单,就是将符合条件的情况除以总共的情况 下面以掷骰子为例: 问题:将一个骰子掷出,666朝上的概率是多少 …...

脉诊之脉象——平脉,常见病脉,七绝脉
平脉与病脉诊脉纲领平人脉象常见病脉浮脉沉脉迟脉数脉虚脉实脉涩脉洪脉细脉滑脉弦脉紧脉长脉短脉弱脉芤脉结脉代脉七绝脉釜沸脉鱼翔脉虾游脉屋漏脉雀啄脉解索脉弹石脉预后诊脉纲领 脉跳动的力度:有力者,气足也。无力者,气不足也。 脉…...
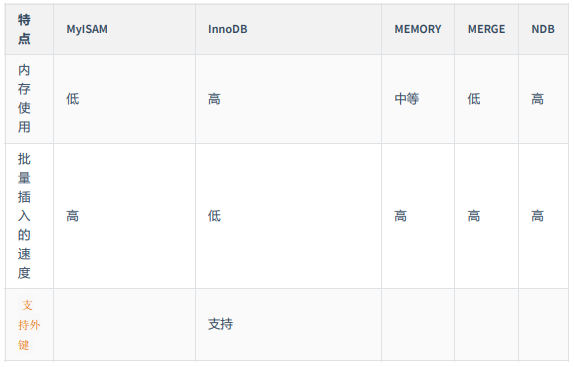
第05章_存储引擎
第05章_存储引擎 🏠个人主页:shark-Gao 🧑个人简介:大家好,我是shark-Gao,一个想要与大家共同进步的男人😉😉 🎉目前状况:23届毕业生,目前在某…...

【新2023Q2押题JAVA】华为OD机试 - 挑选字符串
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:挑选字符串 题目 给定a-z,…...

职场「OKR」,魔幻又内卷
个人习惯称之为【O-KR-KPI】组合; 01从进厂实习那天开始,就接触了KPI的概念; 互联网公司,年初入职,可能因为那天是周五,又赶上月底,少不了要把KPI搬出来折腾一番; 天时,…...

mysql8计算商家距离,按照由近及远排序
要计算商家距离并按照距离排序,可以使用MySQL 8中的空间函数和索引。以下是一个例子: 创建商家表 CREATE TABLE merchants (id INT AUTO_INCREMENT PRIMARY KEY,name VARCHAR(50),location POINT,SPATIAL INDEX (location) ) EngineInnoDB;插入商家数据…...

c语言函数使用记录
1.sscanf函数的用法sscanf():将 C 语言字符串中数据按 指定的格式 将数据存储在对应的参数中。// sscanf() 会从 buffer 里读进数据,依照 format 的格式将数据写入到 argument 里, //注意这里的 argument 需要使用地址符号 // 转换格式参考 s…...

VBA智慧办公4——符号运算及语法结构
目录 运算符 一、算术运算符 二、连接运算符 三、比较运算符 四、逻辑运算符 语法结构 一、if语句 二、select case语句 三、for语句 四、while语句: 五、with语句 运算符 VBA中运算符的作用也是相当重要,本章我们要着重了解VBA中运算符下设的…...

ChatGPT角色扮演提示语
ChatGPT角色扮演提示语 使用ChatGPT角色扮演提示语,你可以将GPT调教成各种专业角色,因此你也会获得更好的对话体验,学会调教GPT,你就会发现GPT实际上非常的强大。此处会长期更新GPT角色提示词,方便各位学习使用GPT… …...

【Java面试题】设计模式之七种结构性模式——代理模式、适配器模式、桥接模式、装饰模式、外观模式、享元模式、组合模式
目录 一、代理模式 二、适配器模式 三、桥接模式 四、装饰模式 五、外观模式 六、享元模式 七、组合模式 一、代理模式 概念: 代理模式是为其他对象提供一种以代理控制对这个对象的访问。在某些情况下,一个对象不适合或者不能直接引用另一个对象࿰…...

【从零开始学习 UVM】6.3、UVM 激励产生 —— start() 方法执行sequence详解
文章目录 start方法解析简单sequence flow继承的seqeunce flow生成sequence flowstart方法解析 virtual task start ( uvm_sequencer_base sequencer,uvm_sequence_base parent_sequence = null,int this_priority = -1...
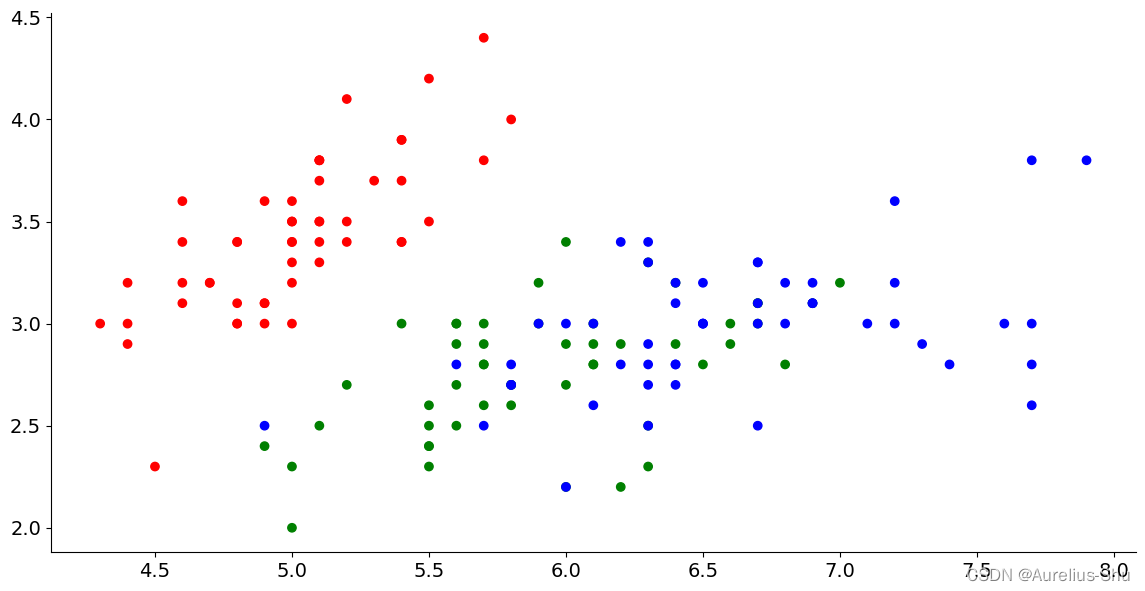
「Python 机器学习」Matplotlib 数据探索
Matplotlib 是一个 Python 的数据可视化库,它能够轻松创建各种类型的图表和图形;Matplotlib 可以在 Jupyter Notebooks、交互式应用程序和脚本中使用,并支持多种绘图样式和格式; Matplotlib 最初是为科学计算而设计的,…...

3.24-3.26学习总结
目录 一.方法methed 二.构造方法(构造器) 三.方法重载 四.方法覆写 一.方法methed 1.定义: 修饰符 方法返回类型 方法名(参数列表){ 系列语句; return 返回值; } 2.public方法/字段: 公开给…...
OpenAI Translator 基于 ChatGPT API 的划词翻译工具
OpenAI Translator,一款基于 ChatGPT API 的划词翻译浏览器插件和跨平台桌面端应用,使用 ChatGPT API 进行划词翻译和文本润色,借助了 ChatGPT 强大的翻译能力,帮助用户更流畅地阅读外语和编辑外语,允许跨 55 种不同语…...

git常用指令---复习向
git常见的指令: 本地仓库 1.创建仓库: git init 会出现.git文件夹 2.查看git状态:git status 3.添加一个文件: git add <fileName> 4.添加所有文件:git add . 5.提交并附加信息:git commit -m&…...

安卓开发学习记录(持续学习)
文章目录前言工具创建项目简单控件即UI一、界面显示与逻辑处理二、文本三、布局四、按钮五、控件综合训练(简易计算器)六、Activity七. 中级控件前言 最近在有在持续学习Java的安卓开发,不断的把知识记录下。 工具 Android Studio安装 [Studio安装][1] [1]: https…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

jdbc查询mysql数据库时,出现id顺序错误的情况
我在repository中的查询语句如下所示,即传入一个List<intager>的数据,返回这些id的问题列表。但是由于数据库查询时ID列表的顺序与预期不一致,会导致返回的id是从小到大排列的,但我不希望这样。 Query("SELECT NEW com…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
