句柄和指针的区别
句柄和指针都是一种数据结构,都常用于访问内存,下面介绍他们的一些不同点。
1 数据结构类型不同
指针的数据类型是无符号整数,占用4或8个字节(在32位和64位系统中),它就像一个变量一样,这个变量存储了一个地址;
而句柄的数据类型实际上是一个结构体,里面存储了数据类型、指向内容的地址和引用数等,如下:
typedef struct {void* ptr; // 指向实际数据对象的指针int type; // 所指数据结构的类型信息int refcnt; // 引用计数
} Handle;
2 特点
由于指针可以直接访问内存中的数据,因此它不具有任何保护机制,随着指针的移动它可以任意访问或修改他所指向的数据结构,这就导致它不太安全;但是,也正因为指针可以直接访问内存地址,因此它也更加灵活高效。
句柄可以用来隐藏实际的内存地址,保护内存中的数据结构,防止非法访问,这使句柄具备一定安全性。但使用句柄访问所指数据结构时,需要通过”解引用“的方式,这就使其访问需要更多时间和资源。
3 使用场景
在需要保护内存中的数据结构的情况下,句柄比较合适;在需要高效访问内存中的数据结构的情况下,指针比较合适。
4 句柄补充
什么是”解引用“?
句柄的解引用是指通过句柄访问存储在句柄中的指针指向的数据。例如,如果句柄中存储了一个指向字符串的指针,那么解引用这个句柄将返回该字符串。
解引用怎么实现的?
class Handle { public:Handle(int* data) : m_data(data) {}~Handle() { delete m_data; }int& operator*() const { return *m_data; }private:int* m_data; };int main() {Handle h(new int(42));int value = *h;std::cout << value << std::endl; // 输出42return 0; }在上面的代码中,Handle类封装了一个指向int类型数据的指针,而operator*函数被用来实现句柄的解引用操作。当对句柄进行解引用时,程序会返回指针所指向的int类型数据,从而实现了句柄的解引用。
句柄中存的信息有什么用?句柄怎么用?
假设有一个名为“Handle”的结构体,其中包含一个指向字符串的指针和一个引用计数。可以使用以下代码创建一个句柄:
Handle* h = new Handle("Hello");这将创建一个指向包含字符串“Hello”的内存的指针,并将其存储在句柄中。引用计数将设置为1。可以使用以下代码解引用句柄并访问该字符串,这将打印出“Hello”:
std::cout << *h << std::endl;可以使用以下代码增加句柄的引用计数:
Handle* h2 = h;h2->AddRef();现在,引用计数为2,因为有两个句柄引用同一块内存。可以使用以下代码减少引用计数:
h->Release();现在,引用计数为1,因为只有一个句柄引用该内存。当所有句柄都被释放时,该内存将被销毁。
相关文章:

句柄和指针的区别
句柄和指针都是一种数据结构,都常用于访问内存,下面介绍他们的一些不同点。 1 数据结构类型不同 指针的数据类型是无符号整数,占用4或8个字节(在32位和64位系统中),它就像一个变量一样,这个变量…...

Linux 网络编程学习笔记——十四、多线程编程
目录 早期 Linux 不支持线程,直到 1996 年,Xavier Leroy 等人才开发出第一个基本符合 POSIX 标准的线程库 LinuxThreads 。但 LinuxThreads 效率低而且问题很多。自内核 2.6 开始,Linux 才真正提供内核级的线程支持,并有两个组织…...

JS 获取时区
JS 获取时区 啥是时区? 时区是地球上的区域使用同一个时间定义。以前,人们通过观察太阳的外置(时角)决定时间,这就使得不同经度的地方的时间各有不同,为了统一使用同一个时间,就引入了时区的概…...

【0183】PG内核客户端认证之将读取的token创建HbaToken(3 - 1)
文章目录 1. 将HbaToken添加到List指针变(续)1.1 示意图的一些问题1.2 修复后的示意图2. 将一行HBA所有字段添加到current_line2.1 代码实现2.2 示意图实现1. 将HbaToken添加到List指针变(续) 在【0182】PG内核客户端认证之将读取的token创建HbaToken(3) 一文中的第3节中…...

别把 OpenAI 太当回事,它远未达到替换前端的地步
最近几个月,我和很多初入行的开发人员交谈,他们对AI越来越感到焦虑。他们看到像GPT-4这样的工具展示的越来越令人印象深刻的演示,担心等他们掌握了HTML/CSS/JS,就没有任何工作机会了。这种情绪现在在Twitter上广泛存在:…...
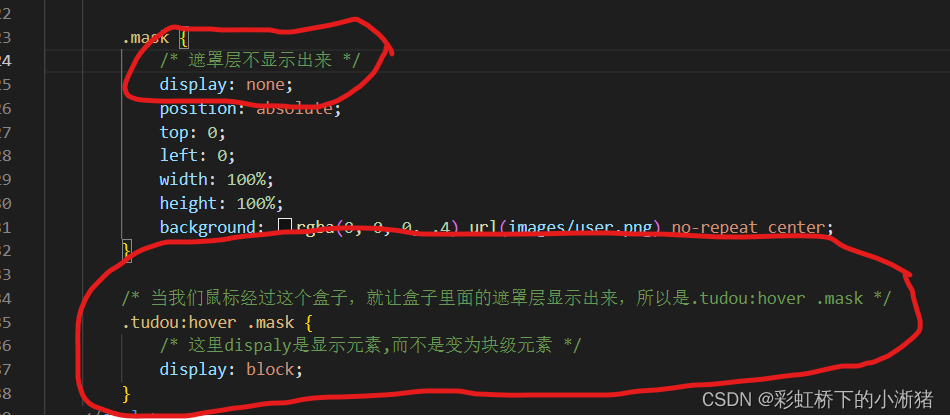
前端基础HTML、CSS--8(CSS-5)
目标: 能够说出为什么要用定位 能够说出定位的4种分类 能够说出4种定位各自的特点 能够说出为什么常用子绝父相布局 能够写出淘宝轮播图布局 能够说出显示隐藏的2种方式以及区别 目录: 定位 综合案例 网页布局总结 元素的显示与隐藏 1.定位 …...
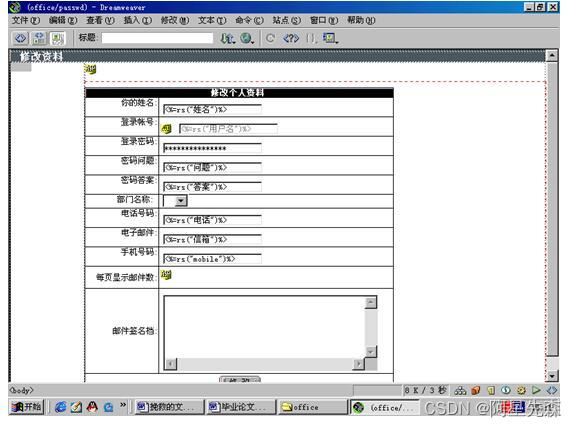
基于ASP网络办公OA系统的设计与实现
本系统是一个企业办公自动化系统,它简单易操作,第一次使用的用户只需申请一个本人的帐户,就可以方便的使用本系统了。 系统的用户分为3类,第一类为普通用户,第二类为管理员,第三类为超级用户。 1通过Web添加文件。操…...
)
C语言计算机二级/C语言期末考试 刷题(五)
收集了一些经典C语言计算机二级和C语言期末考试题库 整理不易,大家点赞收藏支持一下 祝大家计算机二级和期末考试都高分过 系列文章: C语言计算机二级/C语言期末考试 刷题(一) C语言计算机二级/C语言期末考试 刷题(二…...

2023-04-03 grafana-源码编译启动及添加prometheus数据源
摘要: 记录grafana-源码编译启动及添加prometheus数据源 代码仓库: https://github.com/adofsauron/tiflow-dev/tree/main/trunk/grafana-9.4.7 依赖: 必须为go1.19版本,低于此版本则编译报错 go version go1.19.2 linux/amd64 yum install -y yarnpkg 编译: ht…...

微软New Bing(GPT-4)写的Delphi诗歌
你好,这是Bing。我很高兴你对Delphi感兴趣。Delphi是一种编程语言,可以用来开发各种应用程序。我尝试写了一首赞美Delphi的诗歌,希望你喜欢: Delphi,Delphi,你是我的灵感 你让我创造出美妙的程序 你的语法…...
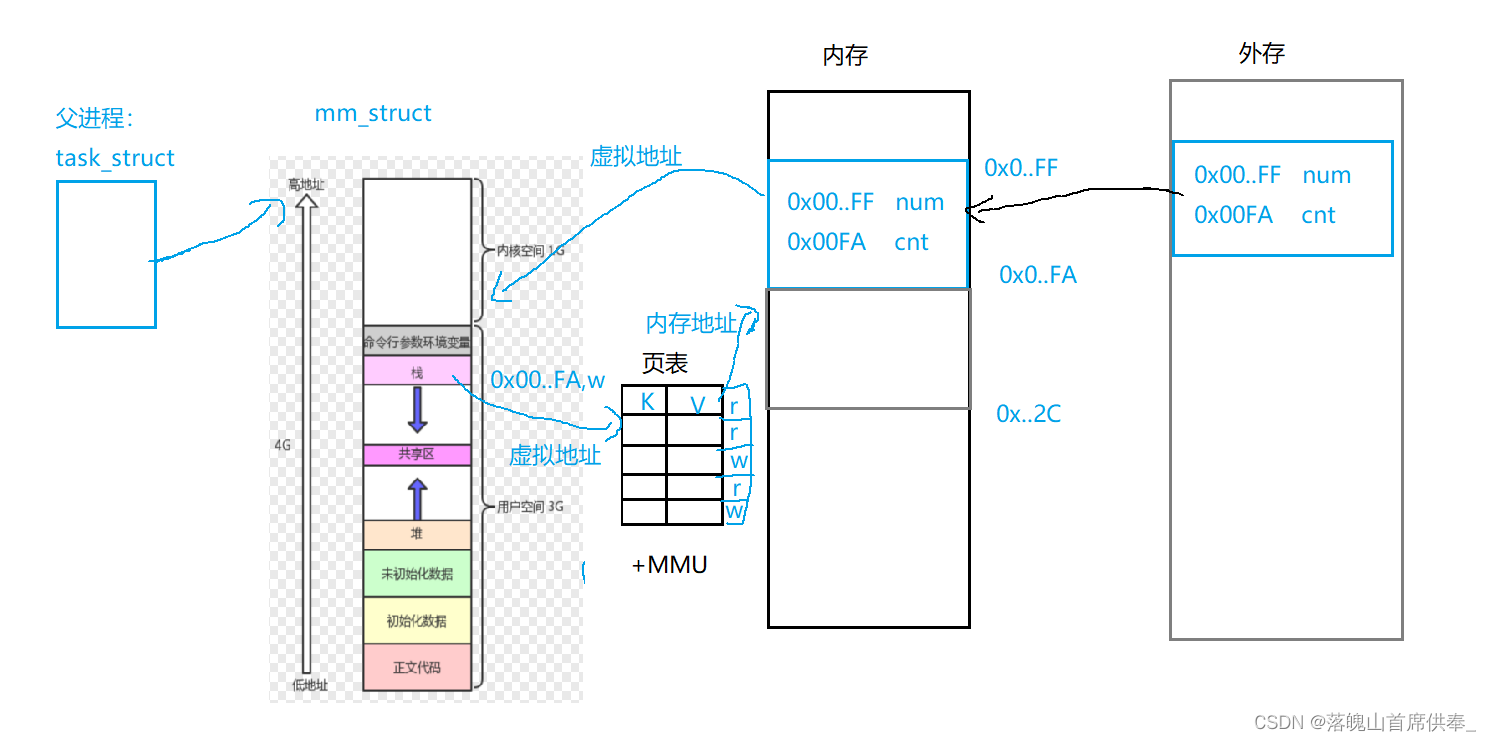
【进程地址空间】
目录:前言一、进程地址空间(一)进程地址空间是什么(二)为什么要有进程地址空间(三)重新理解进程地址空间前言 打怪升级:第52天一、进程地址空间 打怪升级之路开始!&…...
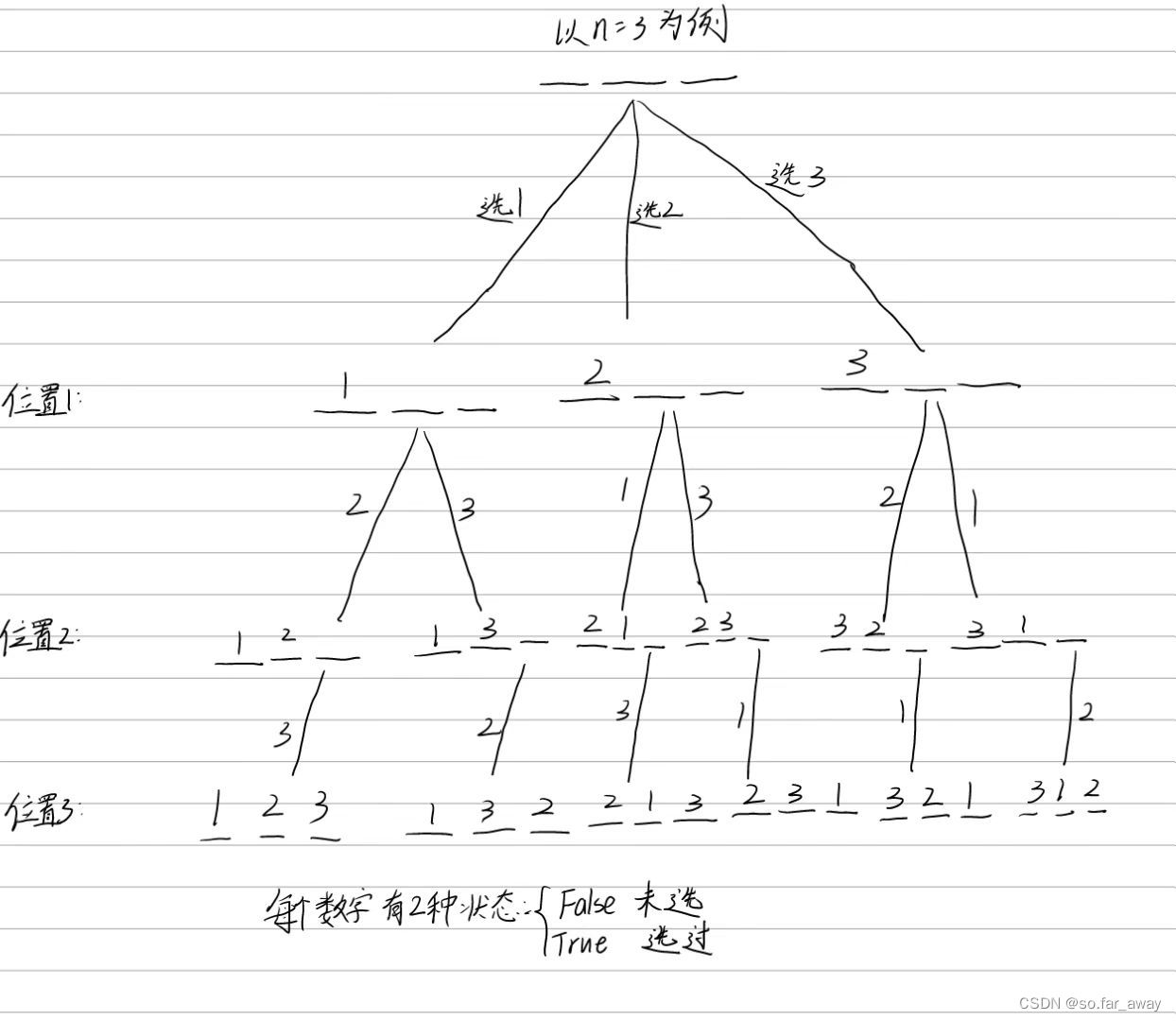
递归dfs入门
做题方法:确定枚举顺序,画出递归树 递归实现指数型枚举 题目编号: acwing.92.递归实现指数型枚举 题目描述: 从 1∼n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。 输入格式: 输入一个整数 n…...

华为OD机试用java实现 -【吃火锅】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:吃火锅 题目 入职后,导师会…...

AI创作优美文章的秘密大揭秘!
随着人工智能技术的快速发展和普及,越来越多的企业和研究机构开始使用AI编程来优化其业务流程和提高效率。AI编程可以被定义为利用人工智能技术来完成特定任务的一种方法。它涵盖了机器学习、深度学习、自然语言处理、计算机视觉等多个领域,可以帮助企业…...
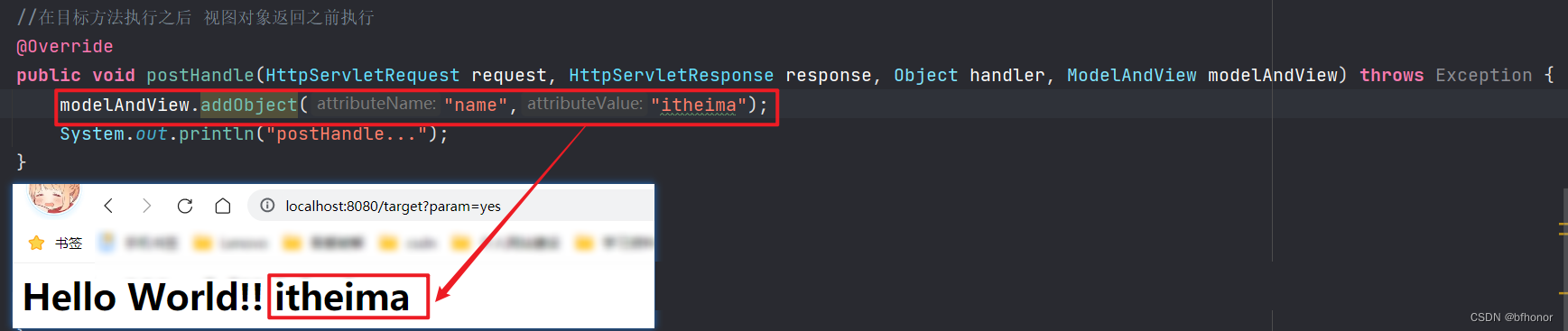
SpringMVC的拦截器
SpringMVC的拦截器 SpringMVC的拦截器SpringMVC的拦截器01-SpringMVC拦截器-拦截器的作用(理解)02-SpringMVC拦截器-interceptor和filter区别(理解,记忆)03-SpringMVC拦截器-快速入门(应用)(1)项目前准备(2)快速入门01…...

dolphinscheduler-3.1.4
1、相关环境 1.1、创建用户,配置免密 useradd hadoop; echo "Hadoop#149" | passwd --stdin hadoop#配置sudo免密 sed -i $ahadoop ALL(ALL) NOPASSWD: NOPASSWD: ALL /etc/sudoers sed -i s/Defaults requirett/#Defaults requirett/g /etc/su…...

大前端05-用vue轻量级第三方组件库快速创建个画板,可以支持画板、直线、圆形等输入,可以撤回,改变颜色
第三方组件介绍: 1. vue-whiteboard vue-whiteboard 是一个基于Vue.js的轻量级画板组件库。 GitHub仓库: https://github.com/craynic/vue-whiteboard 优势: 轻量级支持基本绘图功能,如画线、圆等支持橡皮擦功能支持清空画布 劣势&…...

ChatGPT使用案例之生成PPT
ChatGPT使用案例之生成PPT ChatGPT使用案例系列我们一直在寻找ChatGPT在哪些方面可以可以帮我们节省时间提高效率,越来越多的用户发掘出了ChatGPT更多实用性的功能,其中一项便是协助用户快速生成PPT。 作为一个基于大型语言处理模型的文字聊天工具,ChatGPT能够帮助用户围绕…...

ChatGPT基础知识系列之模型介绍
ChatGPT基础知识系列之模型介绍 前面我们已经介绍很多ChatGPT的使用案例了,更多案例可以参考我们下面的文章 ChatGPT使用案例之写代码 ChatGPT使用案例之画思维导图 ChatGPT使用案例之自然语言处理 ChatGPT使用案例之操作Excel ChatGPT使用案例之图像生成 ChatGPT使用案…...

ChatGPT助力软件开发
抛开Stack Overflow不谈,开发人员有了一个新的好朋友,它就是ChatGPT。ChatGPT是由人工智能驱动的语言模型,可以理解代码,还可以用自然语言回答问题。有了它,程序员再也不用在无尽的Stack Overflow页面和评论中搜索答案…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
