文心一言 VS 讯飞星火 VS chatgpt (361)-- 算法导论24.3 3题
三、假定将 Dijkstra 算法的第4行改为:
4 while |Q|>1
这种改变将让 while 循环的执行次数从 ∣ V ∣ |V| ∣V∣ 次降低到 ∣ V ∣ − 1 |V|-1 ∣V∣−1 次。这样修改后的算法正确吗?
如果要写代码,请用go语言。
文心一言:
将 Dijkstra 算法的第4行从 while |Q| > 0 改为 while |Q| > 1 会导致算法的正确性受到影响。Dijkstra 算法的核心在于每次从当前未处理的顶点集合 Q Q Q 中选择具有最小估计距离的顶点 u u u,并更新从源顶点到其他所有通过 u u u 路径可达的顶点的最短路径估计。
当 while |Q| > 1 时,算法会在 Q Q Q 中还剩下一个或更多顶点时停止。这会导致算法可能无法处理所有顶点,特别是当图中存在多个最短路径或顶点之间存在依赖关系时。例如,如果有两个顶点 v v v 和 w w w,它们的最短路径都依赖于第三个顶点 u u u,而 u u u 的最短路径尚未被处理,那么这种修改后的算法会提前停止,导致结果不正确。
因此,这种修改后的算法是不正确的。
以下是使用 Go 语言编写的标准 Dijkstra 算法的实现,供您参考:
package mainimport ("container/heap""fmt""math"
)// Edge represents a directed edge in the graph
type Edge struct {to intweight int
}// Graph represents a weighted, directed graph
type Graph struct {vertices intedges map[int][]Edge
}// NewGraph creates a new graph with the given number of vertices
func NewGraph(vertices int) *Graph {return &Graph{vertices: vertices,edges: make(map[int][]Edge),}
}// AddEdge adds a directed edge to the graph
func (g *Graph) AddEdge(from, to, weight int) {g.edges[from] = append(g.edges[from], Edge{to, weight})
}// PriorityQueueItem represents an item in the priority queue
type PriorityQueueItem struct {vertex intdistance intindex int
}// PriorityQueue implements heap.Interface and holds PriorityQueueItems.
type PriorityQueue []*PriorityQueueItemfunc (pq PriorityQueue) Len() int { return len(pq) }func (pq PriorityQueue) Less(i, j int) bool {return pq[i].distance < pq[j].distance
}func (pq PriorityQueue) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]pq[i].index = ipq[j].index = j
}func (pq *PriorityQueue) Push(x interface{}) {n := len(*pq)item := x.(*PriorityQueueItem)item.index = n*pq = append(*pq, item)
}func (pq *PriorityQueue) Pop() interface{} {old := *pqn := len(old)item := old[n-1]old[n-1] = nil // avoid memory leakitem.index = -1 // for safety*pq = old[0 : n-1]return item
}func (pq *PriorityQueue) update(item *PriorityQueueItem, vertex, distance int) {item.vertex = vertexitem.distance = distanceheap.Fix(pq, item.index)
}// Dijkstra calculates the shortest paths from the source vertex to all other vertices in the graph
func (g *Graph) Dijkstra(source int) []int {distances := make([]int, g.vertices)for i := range distances {distances[i] = math.MaxInt32}distances[source] = 0pq := make(PriorityQueue, 0, g.vertices)heap.Init(&pq)heap.Push(&pq, &PriorityQueueItem{vertex: source, distance: 0})for pq.Len() > 0 {u := heap.Pop(&pq).(*PriorityQueueItem).vertexfor _, edge := range g.edges[u] {alt := distances[u] + edge.weightif alt < distances[edge.to] {distances[edge.to] = altheap.Push(&pq, &PriorityQueueItem{vertex: edge.to, distance: alt})}}}return distances
}func main() {g := NewGraph(5)g.AddEdge(0, 1, 10)g.AddEdge(0, 4, 5)g.AddEdge(1, 2, 1)g.AddEdge(1, 4, 2)g.AddEdge(2, 3, 4)g.AddEdge(3, 2, 6)g.AddEdge(3, 1, 7)g.AddEdge(4, 1, 3)g.AddEdge(4, 2, 9)g.AddEdge(4, 3, 2)distances := g.Dijkstra(0)for i, d := range distances {fmt.Printf("Distance from source to vertex %d: %d\n", i, d)}
}
这段代码实现了一个标准的 Dijkstra 算法,用于计算从源顶点到图中所有其他顶点的最短路径。您可以运行这段代码来验证算法的正确性。





讯飞星火:
这种改变是不正确的。Dijkstra 算法的目的是找到从源节点到所有其他节点的最短路径。在第4行,我们需要确保在每次迭代中,Q(优先队列)都至少包含一个节点。如果将第4行改为 while |Q|>1,那么在某些情况下,Q 可能只包含一个节点,这将导致算法无法继续执行,从而无法找到所有节点的最短路径。
正确的 Dijkstra 算法实现如下:
package mainimport ("fmt""container/heap"
)type Edge struct {to intcost int
}type Node struct {id intdist intedges []Edge
}type PriorityQueue []*Nodefunc (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {return pq[i].dist < pq[j].dist
}
func (pq PriorityQueue) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {node := x.(*Node)*pq = append(*pq, node)
}
func (pq *PriorityQueue) Pop() interface{} {old := *pqn := len(old)item := old[n-1]*pq = old[0 : n-1]return item
}func dijkstra(nodes []*Node, start int) {pq := make(PriorityQueue, len(nodes))for i := range nodes {pq[i] = nodes[i]}heap.Init(&pq)for pq.Len() > 0 {u := heap.Pop(&pq).(*Node)if u.dist == -1 {continue}for _, edge := range u.edges {v := nodes[edge.to]alt := u.dist + edge.costif alt < v.dist {v.dist = altheap.Fix(&pq, v.id)}}}
}func main() {// 示例图结构nodes := []*Node{{id: 0, dist: 0, edges: []Edge{{to: 1, cost: 4}, {to: 2, cost: 1}}},{id: 1, dist: -1, edges: []Edge{{to: 3, cost: 1}}},{id: 2, dist: -1, edges: []Edge{{to: 1, cost: 2}, {to: 3, cost: 5}}},{id: 3, dist: -1, edges: []Edge{}},}dijkstra(nodes, 0)for _, node := range nodes {fmt.Printf("Node %d: distance = %d\n", node.id, node.dist)}
}
在这个实现中,我们使用了一个优先队列(最小堆)来存储节点,并在每次迭代中弹出距离最小的节点。这样可以确保算法在所有情况下都能正确地找到最短路径。
360智脑:
Dijkstra 算法是一种用于在加权图中找到单源最短路径的算法。原始的 Dijkstra 算法通常是这样的:
1 function Dijkstra(G, S)
2 for each vertex V in G
3 dist[V] <- infinite
4 previous[V] <- NULL
5 add V to Q
6 dist[S] <- 0
7 while Q is not empty
8 U <- vertex in Q with smallest distance in dist[]
9 remove U from Q
10 for each neighbor V of U
11 tempDist <- dist[U] + edge_weight(U, V)
12 if tempDist < dist[V]
13 dist[V] <- tempDist
14 previous[V] <- U
在这个算法中,第7行的 while 循环会一直执行直到队列 Q 为空,这意味着它会处理图中的所有顶点。如果你将第4行改为 while |Q|>1,那么 while 循环将在队列中只剩下一个元素时停止,这通常是源顶点本身。这样的修改会导致算法无法处理所有的顶点,因此是不正确的。
正确的 Dijkstra 算法应该确保处理完除源顶点外的所有顶点,因为源顶点的最短路径总是0,不需要再更新。因此,while 循环应该持续到队列为空,而不是在队列中剩下一个元素时停止。
下面是一个使用 Go 语言实现的 Dijkstra 算法的示例代码,它遵循了原始的算法逻辑:
package mainimport ( "container/heap""fmt"
) type Edge struct {to intweight int
}type Graph [][]Edge type Item struct {value intpriority int index int
}type PriorityQueue []*Itemfunc (pq PriorityQueue) Len() int { return len(pq) }func (pq PriorityQueue) Less(i, j int) bool {return pq[i].priority < pq[j].priority
}func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] pq[i].index = i pq[j].index = j
}func (pq *PriorityQueue) Push(x interface{}) {n := len(*pq) item := x.(*Item)item.index = n *pq = append(*pq, item)
}func (pq *PriorityQueue) Pop() interface{} { old := *pqn := len(old) item := old[n-1]old[n-1] = nil item.index = -1 *pq = old[0 : n-1]return item
}func (pq *PriorityQueue) update(item *Item, value int, priority int) {item.value = valueitem.priority = priorityheap.Fix(pq, item.index)
}func Dijkstra(graph Graph, start int) ([]int, []int) {dist := make([]int, len(graph))for i := range dist { dist[i] = 1<<31 - 1 // 初始化为无穷大} previous := make([]int, len(graph))for i := range previous { previous[i] = -1}pq := make(PriorityQueue, 0) heap.Init(&pq) dist[start] = 0 item := &Item{ value: start,priority: 0, index: 0, }heap.Push(&pq, item) for pq.Len() > 0 { u := heap.Pop(&pq).(*Item)for _, edge := range graph[u.value] {v := edge.to alt := dist[u.value] + edge.weight if alt < dist[v] { dist[v] = alt previous[v] = u.valuepq.update(&Item{value: v, priority: dist[v]}, v, dist[v])}} }return dist, previous
}func main() {// 创建图的邻接表表示 graph := Graph{{{1, 1}, {2, 4}}, {{2, 2}, {3, 6}}, {}, {}}distances, _ := Dijkstra(graph, 0)fmt.Println("Shortest distances from source:", distances)
}
这个 Go 代码实现了一个优先级队列来管理待处理的顶点,并使用了堆数据结构来高效地选择下一个要处理的顶点。请注意,这个实现假设图是无向的,并且每个边都有正权重。如果图是有向的或者包含负权重边,可能需要其他类型的算法,如 Bellman-Ford 算法。
智谱清言:
修改Dijkstra算法的循环条件为 while |Q|>1 是不正确的。Dijkstra算法的正确性依赖于每个顶点从源点出发的最短路径一旦确定就不会再改变,这要求算法在处理完所有顶点之前不能提前终止。原来的循环条件是 while Q is not empty,这确保了算法会处理图中的每个顶点,直到找到从源点到所有其他顶点的最短路径。
将循环条件改为 while |Q|>1 意味着算法将在只剩下一个顶点未处理时停止,这可能会导致算法无法找到所有顶点的最短路径。特别是对于非源点的顶点,如果它们的最短路径是在算法的最后几个迭代中确定的,那么这样的修改会导致这些路径不会被找到。
以下是使用Go语言实现的未经修改的Dijkstra算法示例代码:
package main
import ("container/heap""fmt"
)
// An Item is something we manage in a priority queue.
type Item struct {vertex int // The vertex numberdist float64 // The priority of the item in the queueindex int // The index of the item in the heap; needed by update and is maintained by the heap.Interface methods.
}
// A PriorityQueue implements heap.Interface and holds Items.
type PriorityQueue []*Item
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {// We want Pop to give us the lowest, not highest, priority so we use less than here.return pq[i].dist < pq[j].dist
}
func (pq PriorityQueue) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]pq[i].index = ipq[j].index = j
}
func (pq *PriorityQueue) Push(x interface{}) {n := len(*pq)item := x.(*Item)item.index = n*pq = append(*pq, item)
}
func (pq *PriorityQueue) Pop() interface{} {old := *pqn := len(old)item := old[n-1]old[n-1] = nil // avoid memory leakitem.index = -1 // for safety*pq = old[0 : n-1]return item
}
// update modifies the priority and value of an Item in the queue.
func (pq *PriorityQueue) update(item *Item, dist float64) {item.dist = distheap.Fix(pq, item.index)
}
// Dijkstra algorithm
func Dijkstra(graph map[int]map[int]float64, start int) map[int]float64 {dist := make(map[int]float64)prev := make(map[int]int) // Not used here, but can be used to reconstruct the shortest pathfor v := range graph {dist[v] = float64(^uint(0) >> 1) // Set initial distances to "infinity"}dist[start] = 0pq := make(PriorityQueue, 1)pq[0] = &Item{vertex: start,dist: 0,index: 0,}heap.Init(&pq)for pq.Len() > 0 {item := heap.Pop(&pq).(*Item)u := item.vertexneighbors := graph[u]for v, weight := range neighbors {alt := dist[u] + weightif alt < dist[v] {dist[v] = altprev[v] = uheap.Push(&pq, &Item{vertex: v, dist: alt})}}}return dist
}
func main() {// Example graph represented as an adjacency mapgraph := map[int]map[int]float64{0: {1: 7, 2: 9, 5: 14},1: {0: 7, 2: 10, 3: 15},2: {0: 9, 1: 10, 3: 11, 5: 2},3: {1: 15, 2: 11, 4: 6},4: {3: 6, 5: 9},5: {0: 14, 2: 2, 4: 9},}start := 0distances := Dijkstra(graph, start)fmt.Println("Vertex\tDistance from Source")for vertex, distance := range distances {fmt.Printf("%d\t%.2f\n", vertex, distance)}
}
这段代码实现了Dijkstra算法,并使用优先队列(通过Go的container/heap包实现)来选择下一个访问的顶点。它
天工:
修改 Dijkstra 算法中的 while 循环条件从传统的 |Q| > 0 到 |Q| > 1 并不会保证算法的正确性。原始 Dijkstra 算法中,循环会持续进行直到优先队列 Q 变为空,即所有顶点都被处理过。这是因为 Dijkstra 算法需要确保从源点到每个顶点的最短路径都被正确计算。
如果将条件改为 |Q| > 1,则当队列中只剩下最后一个顶点时,循环会提前结束。这可能导致以下问题:
- 最后一个顶点的最短路径可能没有被正确计算,因为它依赖于之前顶点的最短路径信息。
- 算法可能无法正确处理图中所有顶点,特别是那些与源点不直接相连的顶点。
正确的 Go 语言代码示例
下面是一个使用标准 Dijkstra 算法的 Go 语言实现示例,它正确处理了所有顶点,直到优先队列为空。
package mainimport ("container/heap""fmt"
)type Node struct {index intdist int
}type PriorityQueue []*Nodefunc (pq PriorityQueue) Len() int { return len(pq) }func (pq PriorityQueue) Less(i, j int) bool {return pq[i].dist < pq[j].dist
}func (pq PriorityQueue) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]
}func (pq *PriorityQueue) Push(x interface{}) {node := x.(*Node)*pq = append(*pq, node)
}func (pq *PriorityQueue) Pop() interface{} {old := *pqn := len(old)node := old[n-1]*pq = old[0 : n-1]return node
}func dijkstra(graph [][]int, source int) []int {dist := make([]int, len(graph))for i := range dist {dist[i] = 99999}dist[source] = 0pq := make(PriorityQueue, 0)heap.Push(&pq, &Node{index: source, dist: 0})for pq.Len() > 0 {current := heap.Pop(&pq).(*Node)for v, w := range graph[current.index] {if w > 0 && dist[v] > dist[current.index]+w {dist[v] = dist[current.index] + wheap.Push(&pq, &Node{index: v, dist: dist[v]})}}}return dist
}func main() {graph := [][]int{{0, 10, 20, 0},{10, 0, 5, 1},{20, 5, 0, 2},{0, 1, 2, 0},}source := 0dist := dijkstra(graph, source)fmt.Println("Shortest distances from source:", dist)
}
这段代码使用了 Go 语言的 container/heap 包来实现优先队列,确保了算法的正确性和效率。
chatgpt:
修改Dijkstra算法的第4行为while |Q|>1会导致在最后一次循环中直接跳过最后一个节点的处理,因此会导致算法结果不正确。
以下是一个基于原始Dijkstra算法的Go语言实现示例:
package mainimport ("fmt""math"
)type Graph struct {nodes []stringedges map[string]map[string]int
}func Dijkstra(graph Graph, start string) map[string]int {dist := make(map[string]int)visited := make(map[string]bool)for _, node := range graph.nodes {dist[node] = math.MaxInt64}dist[start] = 0for len(visited) < len(graph.nodes) {u := minDistance(dist, visited)visited[u] = truefor v, weight := range graph.edges[u] {if !visited[v] && dist[u]+weight < dist[v] {dist[v] = dist[u] + weight}}}return dist
}func minDistance(dist map[string]int, visited map[string]bool) string {min := math.MaxInt64minNode := ""for node, distance := range dist {if !visited[node] && distance < min {min = distanceminNode = node}}return minNode
}func main() {graph := Graph{nodes: []string{"A", "B", "C", "D", "E"},edges: map[string]map[string]int{"A": {"B": 1, "C": 4},"B": {"C": 2, "D": 5},"C": {"D": 1, "E": 3},"D": {"E": 1},"E": {},},}distances := Dijkstra(graph, "A")fmt.Println(distances)
}
请注意,这里使用了原始的Dijkstra算法实现,未进行上述所提到的修改。
kimi:
Dijkstra算法是一种用于在加权图中找到单个源点到所有其他顶点的最短路径的算法。其基本思想是贪心策略,即在每一步都选择当前未确定最短路径的顶点中距离源点最近的一个,更新其相邻顶点的最短路径。
原始的Dijkstra算法的while循环条件通常是检查队列Q是否非空,即while Q。这是因为算法需要从源点开始,逐步扩展到所有顶点,直到所有的顶点都被访问过。
如果你将条件改为while |Q| > 1,这意味着只要队列中有多于一个元素,循环就会继续。这种修改会导致算法在只剩下一个顶点时停止,而这个顶点可能是源点本身。如果源点没有与任何其他顶点相连,那么算法将不会正确地计算出到其他所有顶点的最短路径。
因此,这种修改是不正确的,因为它违反了算法的贪心策略,可能导致算法提前终止,没有计算出所有顶点的最短路径。
下面是用Go语言实现的Dijkstra算法的一个简单示例:
package mainimport ("fmt""math"
)type Graph struct {adjMatrix [][]intsize int
}func (g *Graph) Dijkstra(s int) []int {dist := make([]int, g.size)visited := make([]bool, g.size)for i := range dist {dist[i] = math.MaxInt32}dist[s] = 0for len(visited) > 0 {min := math.MaxInt32u := -1for v := range dist {if !visited[v] && dist[v] < min {min = dist[v]u = v}}if u == -1 {break}visited[u] = truefor v := range g.adjMatrix[u] {if g.adjMatrix[u][v] != 0 {if dist[u]+g.adjMatrix[u][v] < dist[v] {dist[v] = dist[u] + g.adjMatrix[u][v]}}}}return dist
}func main() {// Example graph represented as an adjacency matrixgraph := &Graph{adjMatrix: [][]int{{0, 6, 0, 1, 0, 0},{6, 0, 5, 2, 2, 2},{0, 5, 0, 0, 0, 5},{1, 2, 0, 0, 4, 0},{0, 2, 0, 4, 0, 6},{0, 2, 5, 0, 6, 0},},size: 6,}distances := graph.Dijkstra(0)fmt.Println("The shortest distances from the source vertex are:", distances)
}
在这个代码中,我们定义了一个Graph结构体,它包含了邻接矩阵和顶点的数量。Dijkstra方法实现了Dijkstra算法,它返回一个整数切片,表示从源点到每个顶点的最短距离。在main函数中,我们创建了一个图的实例,并调用Dijkstra方法来计算从源点(这里是顶点0)到所有其他顶点的最短路径。
混元:
将 Dijkstra 算法的第4行改为 while |Q|>1 会导致算法提前结束,因为当队列中只剩下一个元素时,循环就会停止。这可能会导致算法无法找到从源节点到所有其他节点的最短路径,特别是当图中存在负权重边时。
Dijkstra 算法的基本思想是每次从优先队列中取出距离源节点最近的节点,并更新其邻居节点的距离。如果图中存在负权重边,Dijkstra 算法可能无法正确处理,因为它假设一旦一个节点被处理,它的最短路径就确定了。
下面是使用 Go 语言实现的 Dijkstra 算法,其中包含了优先队列的实现:
package mainimport ("container/heap""fmt"
)type Edge struct {to, weight int
}type PriorityQueue []*Itemtype Item struct {value intpriority intindex int
}func (pq PriorityQueue) Len() int { return len(pq) }func (pq PriorityQueue) Less(i, j int) bool {return pq[i].priority < pq[j].priority
}func (pq PriorityQueue) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]pq[i].index = ipq[j].index = j
}func (pq *PriorityQueue) Push(x interface{}) {n := len(*pq)item := x.(*Item)item.index = n*pq = append(*pq, item)
}func (pq *PriorityQueue) Pop() interface{} {old := *pqn := len(old)item := old[n-1]old[n-1] = nilitem.index = -1*pq = old[0 : n-1]return item
}func dijkstra(graph [][]Edge, start int) []int {n := len(graph)dist := make([]int, n)for i := range dist {dist[i] = 1e9}dist[start] = 0pq := make(PriorityQueue, 0)heap.Push(&pq, &Item{value: start, priority: 0})for pq.Len() > 0 {item := heap.Pop(&pq).(*Item)u := item.valuefor _, edge := range graph[u] {v := edge.toif dist[v] > dist[u]+edge.weight {dist[v] = dist[u] + edge.weightheap.Push(&pq, &Item{value: v, priority: dist[v]})}}}return dist
}func main() {graph := [][]Edge{{{1, 4}, {2, 1}},{{3, 1}},{{1, 2}, {3, 5}},{},}dist := dijkstra(graph, 0)fmt.Println(dist) // Output: [0 3 1 4]
}
在这个实现中,我们使用了 Go 语言的 container/heap 包来实现优先队列。Dijkstra 算法的 while 循环条件是 pq.Len() > 0,这意味着只要优先队列中还有元素,循环就会继续执行。这样可以确保算法能够找到从源节点到所有其他节点的最短路径。
总之,将 Dijkstra 算法的第4行改为 while |Q|>1 是不正确的,因为这可能会导致算法无法正确处理所有情况。正确的实现应该是 while pq.Len() > 0。
相关文章:

文心一言 VS 讯飞星火 VS chatgpt (361)-- 算法导论24.3 3题
三、假定将 Dijkstra 算法的第4行改为: 4 while |Q|>1 这种改变将让 while 循环的执行次数从 ∣ V ∣ |V| ∣V∣ 次降低到 ∣ V ∣ − 1 |V|-1 ∣V∣−1 次。这样修改后的算法正确吗? 如果要写代码,请用go语言。 文心一言: 将 Dijkst…...

ArkTS 开发中,有两种网络请求
在鸿蒙开发中,ArkTS(Ark TypeScript)是用于构建鸿蒙应用的一种开发语言,它基于TypeScript,并提供了丰富的API和工具集来简化开发过程。其中,网络请求是开发应用时经常需要用到的一个功能。 ArkTS 网络请求…...

记录一次病毒启动脚本
在第一次下载软件时,目录中配了一个使用说明,说是需要通过start.bat 这个文件来启动程序,而这个 start.bat 就是始作俑者: 病毒作者比较狡猾,其中start.bat 用记事本打开是乱码,但是可以通过将这个批处理…...

2019~2023博文汇总目录
2023 大厂实践 - 哈啰:记录一次ElasticSearch的查询性能优化-CSDN博客 Shiro安全框架-CSDN博客 MQ知识点汇总-CSDN博客 工作学习记录-CSDN博客 后端架构师技术图谱-CSDN博客 2020 Elasticsearch相关技术点_elasticsearch技术点-CSDN博客 Kafka相关技术点_kafka…...

springboot项目配置部分依赖从私服拉取,部分从阿里云拉取
在Java项目中,配置部分依赖从私服拉取,部分从阿里云拉取,可以在Maven的配置文件settings.xml中设置多个镜像,Maven会根据镜像的顺序尝试下载依赖。 配置私服镜像:首先配置你的私服镜像,例如Nexus私服&…...

返回索引对象中各元素的数据类型 pandas.Index.dtype
【小白从小学Python、C、Java】 【考研初试复试毕业设计】 【Python基础AI数据分析】 返回索引对象中 各元素的数据类型 pandas.Index.dtype [太阳]选择题 根据题目代码,执行idx3.dtype的结果是? import pandas as pd idx1 pd.Index([1, 2, 3, 4, 5])…...
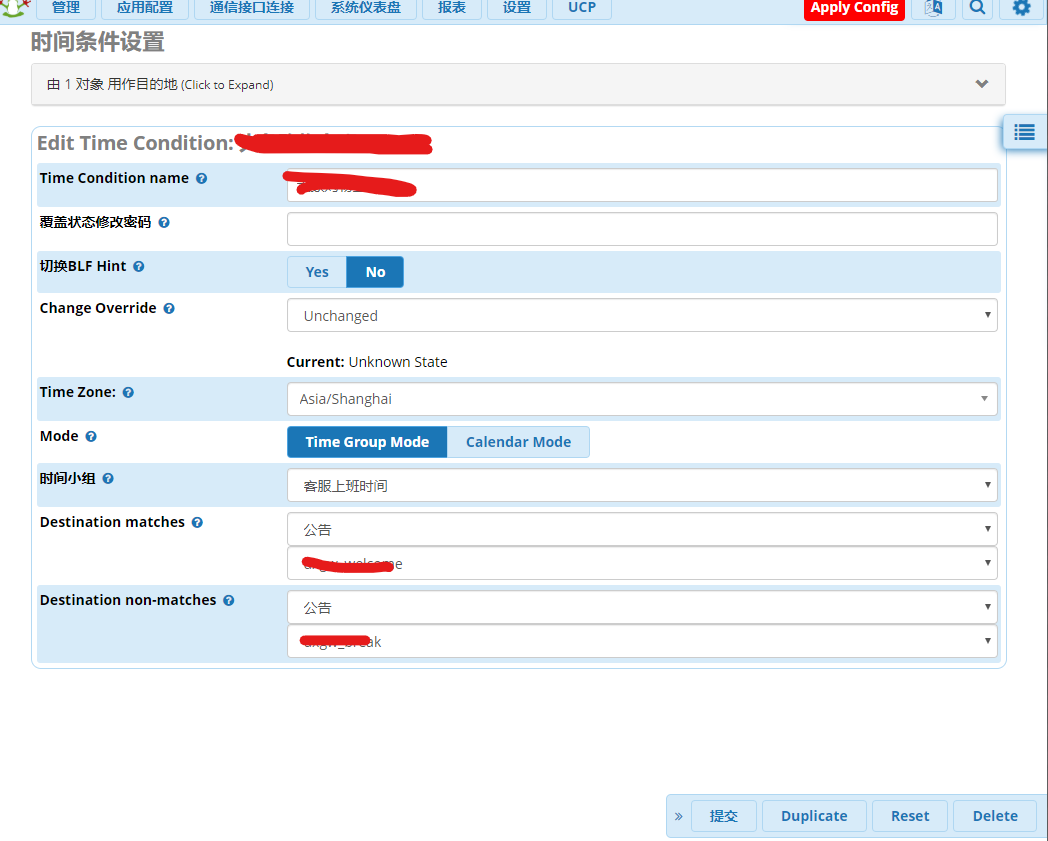
通过freepbx搭建小型电话系统的过程
领导说公司的客服电话需要实现语音导航和非工作时间自动接听播放语音提示的功能。任务自然落到了伟大的程序员的头上,本着为公司节约成本原则遂百度了一番,找到了asterisk 和freeswitch两个比较流行的电话系统。经过对比和考虑公司的情况选择了asterisk系…...

pdf处理1
处理PDF文件以构建数据索引是一个复杂但关键的步骤,尤其是因为PDF格式的文件通常包含多种元素,如文本、图片、表格、标题等。以下是一个通俗易懂的详细解释,帮助你理解PDF文件是如何被处理和解析的: 1. PDF文件的基本结构 PDF&a…...
)
区间覆盖(贪心)
给定 NN 个闭区间 [ai,bi][ai,bi] 以及一个线段区间 [s,t][s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。 输出最少区间数,如果无法完全覆盖则输出 −1−1。 输入格式 第一行包含两个整数 ss 和 tt,表示给定线段区间的两…...

[rk3588 debain]cpu死锁问题解决
1 问题 rk3588机器上运行客户如下程序程序发生“BUG: spinlock recursion on CPU#0” ./rtsp RtspWrapper.xml 应用程序功能是:ip摄像头推流,通过rtsp协议拉流,对视频流做裁剪,缩放工作。首先,根据视频帧率每秒钟处理…...

CMU 10423 Generative AI:lec18(大模型的分布式训练)
这个文档主要讲解了分布式训练(Distributed Training),特别是如何在多GPU上训练大规模的语言模型。以下是主要内容的概述: 1. 问题背景 训练大规模语言模型的主要挑战是内存消耗。 训练过程中,内存消耗主要来源于两个…...

项目级别的配置文件 `.git/config`||全局配置文件 `~/.gitconfig`
Git 项目级别的配置文件 .git/config,该文件包含了当前项目(仓库)的特定配置。 与全局配置文件 ~/.gitconfig 不同,这里的设置仅对当前项目生效。 配置内容解释 [core]repositoryformatversion 0filemode truebare falselog…...

【Docker】配置文件
问题 学习Docker期间会涉及到docker的很多配置文件,可能会涉及到的会有: /usr/lib/systemd/system/docker.service 【docker用于被systemd管理的配置文件】 /etc/systemd/system/docker.service.d【覆盖配置文件的存放处】 /etc/systemd/system/mul…...

坐标系变换总结
二维情况下的转换 1 缩放变换 形象理解就是图像在x方向和y方向上放大或者缩小。 代数形式: { x ′ k x x y ′ k y y \begin{cases} x k_x x \\ y k_y y \end{cases} {x′kxxy′kyy 矩阵形式: ( x ′ y ′ ) ( k x 0 0 k y ) ( x y ) \be…...

数据在内存中的存储【上】
一.整型在内存中的存储 在讲解操作符的时候,我们就讲过了下面的内容: 整数的2进制表示方法有三种,即 原码、反码和补码 有符号的整数,三种表示方法均有符号位和数值位两部分,符号位都是用0表示"正"ÿ…...

Prometheus之Pushgateway使用
Pushgateway属于整个架构图的这一部分 The Pushgateway is an intermediary service which allows you to push metrics from jobs which cannot be scraped. The Prometheus Pushgateway exists to allow ephemeral and batch jobs to expose their metrics to Prometheus. S…...

Rust Web开发常用库
本集合中所有库都是在开源项目中广泛使用且在2024年积极维护的库,排名靠前的库是当前使用比较广泛的,不全面但够用 Rust异步运行时 tokio:异步运行时 async_std:与标准库兼容性较强的运行时 monoio:字节开源 smol…...

ios内购支付-支付宝APP支付提现
文章目录 前言一、IOS内购支付(ios订单生成自己写逻辑即可)1.支付回调票据校验controller1.支付回调票据校验server 二、安卓APP支付宝支付1.生成订单返回支付宝字符串(用于app拉起支付宝,这里用的是证书模式)2.生成订…...

新课发布|鸿蒙HarmonyOS Next商城APP应用开发实战
2024年年初,鸿蒙HarmonyOS Next星河版强势发布,随着鸿蒙系统的普及和应用场景的拓展,市场需求将持续增加。鸿蒙系统已经应用于华为的智能手机、平板电脑、智能家居等多个领域,并有望在未来拓展到智能汽车、物联网等更多领域。这为…...

基于Java,SpringBoot,Vue智慧校园健康驿站体检论坛请假管理系统
摘要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播,搭配信息管理工具可以很好地为人们提供服务。针对信息管理混乱,出错率高,信息安全性差…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
