是否是 2 的幂次方
给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。
如果存在一个整数 x 使得 n == 2x ,则认为 n 是 2 的幂次方。
示例 1:
输入:n = 1 输出:true 解释:20 = 1
示例 2:
输入:n = 16 输出:true 解释:24 = 16
示例 3:
输入:n = 3 输出:false
提示:
-231 <= n <= 231 - 1
class Solution {
public:bool isPowerOfTwo(int n) {return n > 0 && (n & (n - 1)) == 0;
}
}; 这里的 & 是按位与(bitwise AND)运算符:& 运算符会在两个数的二进制表示中逐位进行比较,只有当对应位都是 1 时,结果位才是 1,否则结果位是 0。
- 如果
n是 2 的幂次方,它的二进制表示中只有 1 个 1,并且这个 1 是在某个固定位置,其余所有位都是 0。例如:- 1 的二进制表示:
0001 - 2 的二进制表示:
0010 - 4 的二进制表示:
0100 - 8 的二进制表示:
1000
- 1 的二进制表示:
n - 1会将原来唯一的 1 变为 0,并且把它右边的所有位都变为 1。例如:- 对于
n = 8(1000),n - 1 = 7(0111) - 对于
n = 4(0100),n - 1 = 3(0011) - 对于
n = 2(0010),n - 1 = 1(0001)
- 对于
当 n 是 2 的幂次方时,n 和 n - 1 在二进制表示中没有任何相同的 1 位,所以 n & (n - 1) 结果为 0。
相关文章:

是否是 2 的幂次方
给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。 如果存在一个整数 x 使得 n 2x ,则认为 n 是 2 的幂次方。 示例 1: 输入:n 1 输出:tr…...

音视频入门
一个视频,一秒内普遍大于等于25帧。 入门知识: 1.帧,一张画面就是一帧。一个视频就是由许许多多帧组成的。 帧率,单位时间内帧的数量。单位:帧/秒 或 fps。 分类:I帧,P帧,B帧 I…...

C++随心记 续一
C中的模板 在其它语言中如Java或者C#中可能叫做泛型,在C中为模板,泛型的限制通常比模板多。模板可以解决多次的代码重复问题,如以下场景 #include <iostream> #include <string>void print(int value) {std::cout << val…...

消息中间件:RabbitMQ
消息中间件:RabbitMQ 前言安装Window安装Linux安装 管理页面什么是RabbitMQ?入门基本概念简单队列工作队列(Work Queues)发布/订阅(Publish/Subscribe)临时队列 路由(Routing)主题&a…...

sql-labs:42~65
less42(单引号闭合、报错回显) login_useradmin login_password123 and if(11,sleep(2),1) # # 单引号闭合 login_useradmin login_password123and updatexml(1,concat(0x7e,database(),0x7e),1)# # 报错回显…...

KaTeX.js渲染数学公式
什么是KaTeX.js ? KaTeX 是一个集成速度快且功能丰富的数学公式渲染库,专为 Web 设计。它由 Khan Academy 开发,提供接近印刷品质的数学公式展示,同时保持与浏览器的高效互动性。KaTeX 特点包括快速渲染速度、高质量的输出、独立运行、跨平…...

算法训练营打卡Day19
目录 1.二叉搜索树的最近公共祖先 2.二叉树中的插入操作 3.删除二叉搜索树中的节点 题目1、二叉搜索树的最近公共祖先 力扣题目链接(opens new window) 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有…...

H.264编解码工具 - FFmpeg
一、简介 FFmpeg是一款用于处理多媒体数据的开源软件,可以完成音频、视频和多媒体流的编解码、转码、解码、录制、流媒体播放等功能。它提供了丰富的命令行工具和库函数,适用于各种平台和操作系统。 FFmpeg支持多种常见的音视频格式,包括MP3、WAV、FLAC、MP4、AVI、MKV等。它…...

60 序列到序列学习(seq2seq)_by《李沐:动手学深度学习v2》pytorch版
系列文章目录 文章目录 系列文章目录一、理论知识比喻机器翻译Seq2seq编码器-解码器细节训练衡量生成序列的好坏的BLEU(值越大越好)总结 二、代码编码器解码器损失函数训练预测预测序列的评估小结练习 一、理论知识 比喻 seq2seq就像RNN的转录工作一样,非常形象的比…...

elementPlus的tree组件点击后有白色背景
在使用elementPlus的tree组件时,需要对它进行样式的重写,下面是相关代码 <script setup> import { ref } from vue const data [{label: Level one 1,children: [{label: Level two 1-1,children: [{label: Level three 1-1-1}]}]},{label: Leve…...

【Git】Git在Unity中使用时的问题记录
个人向笔记。 (为什么没截图,因为公司电脑没法截图!) 1 前言 主要记录在使用Git协同开发时的各种问题,方便以后查阅。 2 记录 2.1 合并冲突 git pull下来后直接给合并了,麻了。若不想直接合并应该先把分…...

python学习记录6
(1)循环嵌套 可以将一个循环语句所属的语句块也可以是一个完整的一个循环语句,一般嵌套不应该超过3层。 嵌套可以是while-while、for-for,也可以是while-for。 基本图形输出:正方形,直角三角形 #输入一个数字n&…...

MongoDB 的基本使用
目录 数据库的创建和删除 创建数据库 查看数据库 删除数据库 集合的创建和删除 显示创建 查看 删除集合 隐式创建 文档的插入和查询 单个文档的插入 insertOne insertMany 查询 嵌入式文档 查询数组 查询数组元素 为数组元素指定多个条件 通过对数组元素使…...

数据揭秘:分类与预测技术在商业洞察中的应用与实践
分类与预测:数据挖掘中的关键任务 在数据挖掘的广阔天地中,分类与预测就像是一对互补的探险家,它们携手深入数据的丛 林,揭示隐藏的宝藏。 一、分类:数据的归类大师 分类是一种将数据点按照特定的属性或特征划分到不…...

学MybatisPlus
1.设置MySql的数据库 spring:datasource:url: jdbc:mysql://127.0.0.1:3306/mp?useUnicodetrue&characterEncodingUTF-8&autoReconnecttrue&serverTimezoneAsia/Shanghaidriver-class-name: com.mysql.cj.jdbc.Driverusername: rootpassword: MySQL123 logging:l…...
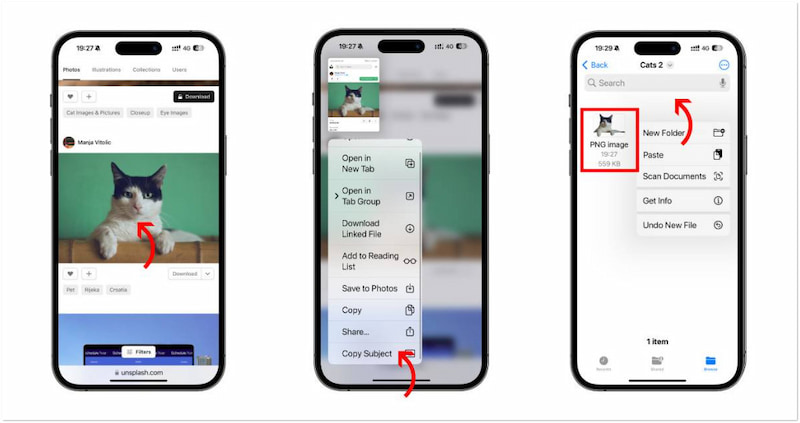
如何使用工具删除 iPhone 上的图片背景
在 iPhone 上删除背景图像变得简单易行。感谢最近 iOS 更新中引入的新功能。如今,iOS 用户现在可以毫不费力地删除背景,而无需复杂的应用程序。在这篇文章中,您将学习如何使用各种方法去除 iPhone 上的背景。这可确保您可以选择最适合您偏好的…...
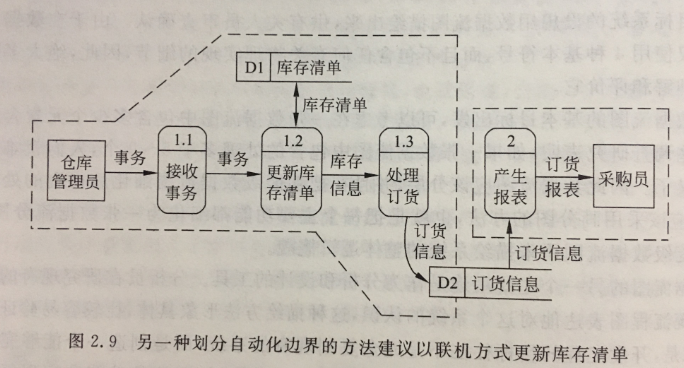
软件工程-数据流图
数据流图(Data Flow Diagram,DFD)是一种图形化技术,它描绘信息流和数据从输入移动到输出的过程中所经受的变换。 数据流图的设计原则 数据守恒原则,对于任何一个加工来说,其所有输出数据流中的数据必须能从该加工的输入数据流中…...

链式前向星(最通俗易懂的讲解)
链式前向新:用于存储图的 边集 数组 前言 当我们存储图的时候,往往会使用 邻接矩阵 或是 邻接表。 邻接矩阵 好写,但太浪费空间,节点一多就存不下; 邻接表 效率高,但涉及指 ,不好写容易出错…...
创建型模式:简单工厂模式,工厂方法模式,抽象工厂模式)
【C++设计模式】(四)创建型模式:简单工厂模式,工厂方法模式,抽象工厂模式
文章目录 (四)创建型模式:简单工厂模式,工厂方法模式,抽象工厂模式简单工厂模式工厂方法模式抽象工厂模式 (四)创建型模式:简单工厂模式,工厂方法模式,抽象工…...
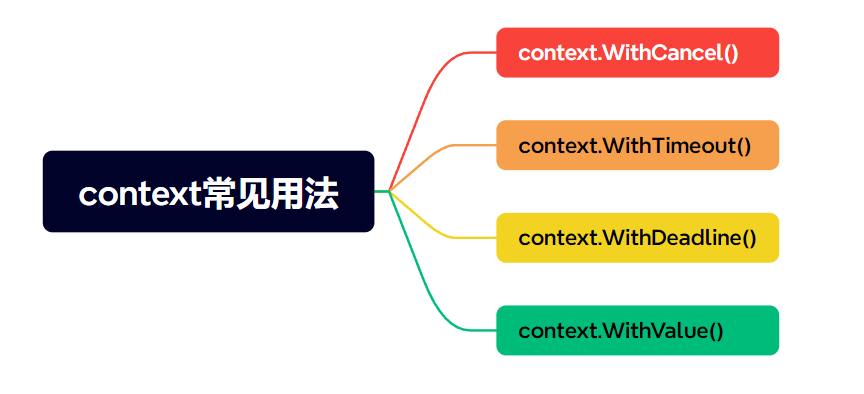
浅析Golang的Context
文章目录 1. 简介2. 常见用法2.1 控制goroutine的生命周期(cancel)2.2 传递超时(Timeout)信息2.3 传递截止时间(Deadline)2.4 传递请求范围内的全局数据 (value) 3 特点3.1 上下文的…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
