【pytorch】范数的计算
近日在看沐神的《动手学深度学习》,其中提到了范数这一数学概念,感觉很陌生,参考ChatGPT补一下知识。
目录
- 范数
- 示例 1: 计算向量的 L2 范数(欧几里得范数)
- 示例 2: 计算矩阵的 Frobenius 范数
- 示例 3: 计算向量的 L1 范数(曼哈顿距离)
- 曼哈顿范数的定义
- 曼哈顿范数的计算示例
- 在Python中计算曼哈顿范数
- 使用NumPy
- 使用PyTorch
- 示例 4: 计算向量的无穷范数(最大值范数)
- 示例 5: 计算矩阵的列范数
- 示例 6: 计算矩阵的行范数
- 示例 7: 计算高维张量的整体范数
- 示例 8: 沿特定维度计算高维张量的范数
- 示例 9: 沿多个维度计算高维张量的范数
范数
让我们通过具体的示例来详细说明如何使用 torch.linalg.norm 计算不同类型的范数,以及如何处理高维张量。
示例 1: 计算向量的 L2 范数(欧几里得范数)
import torch# 创建一个向量
vector = torch.tensor([3.0, 4.0])# 计算 L2 范数
l2_norm = torch.linalg.norm(vector, ord=2)print(f"L2 范数: {l2_norm}") # 输出: 5.0
在这个例子中,计算的是向量 [3.0, 4.0] 的 L2 范数,其结果是 5.0。
此处使用的是L2范数,也是norm的默认设置,其实就是平方根,类似于勾股定理的结果。
示例 2: 计算矩阵的 Frobenius 范数
# 创建一个矩阵
matrix = torch.tensor([[1.0, 2.0], [3.0, 4.0]])# 计算 Frobenius 范数
frobenius_norm = torch.linalg.norm(matrix, ord='fro')print(f"Frobenius 范数: {frobenius_norm}") # 输出: 5.4772
在这个例子中,计算的是矩阵的 Frobenius 范数,即矩阵中所有元素的平方和的平方根。上面的结果也就是30的开方。
示例 3: 计算向量的 L1 范数(曼哈顿距离)
# 创建一个向量
vector = torch.tensor([3.0, 4.0]相关文章:

【pytorch】范数的计算
近日在看沐神的《动手学深度学习》,其中提到了范数这一数学概念,感觉很陌生,参考ChatGPT补一下知识。 目录 范数示例 1: 计算向量的 L2 范数(欧几里得范数)示例 2: 计算矩阵的 Frobenius 范数示例 3: 计算向量的 L1 范数(曼哈顿距离)曼哈顿范数的定义曼哈顿范数的计算示…...
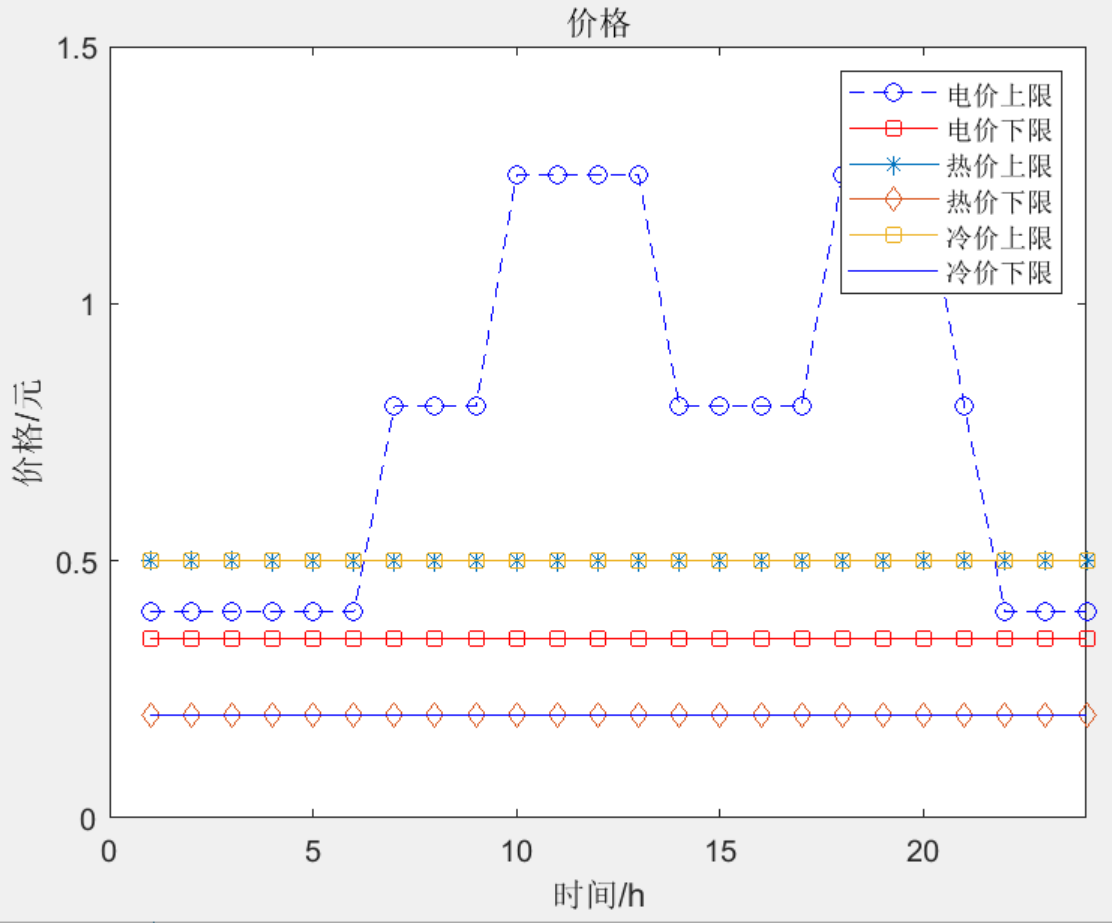
MATLAB|基于多主体主从博弈的区域综合能源系统低碳经济优化调度
目录 主要内容 程序亮点: 模型研究 一、综合能源模型 二、主从博弈框架 部分代码 结果一览 下载链接 主要内容 程序参考文献《基于多主体主从博弈的区域综合能源系统低碳经济优化调度》,采用了区域综合能源系统多主体博弈协同优化方…...
Django 后端数据传给前端
Step 1 创建一个数据库 Step 2 在Django中点击数据库连接 Step 3 连接成功 Step 4 settings中找DATABASES Step 5 将数据库挂上面 将数据库引擎和数据库名改成自己的 Step 6 在_init_.py中加上数据库的支持语句 import pymysql pymysql.install_as_MySQLdb() Step7 简单创建两…...
)
elasticsearch 写入新数据测试(二)
背景:elasticsearch单个node节点写入数据-CSDN博客 需要设置密码才能作为外部调用,不设置我不会用。设置方法见上一篇。 设置密码出现如下问题: Unexpected response code [503] from calling PUT http://172.19.0.1:9200/_security/user/apm_system/_password?pretty …...

android navigation 用法详细使用
Navigation 的关键概念 1、Navigation Graph: 定义了应用内的所有导航目的地以及它们之间的连接。 2、NavHost: 一个 UI 元素,用于承载当前的导航目的地。 3、NavController: 管理目的地之间的导航。 4、Destination: 导航图中的一个节点,用户导航到该节…...

uni-app在线预览pdf
这里推荐下载pdf.js 插件 PDF.js - Browse Files at SourceForge.net 特此注意 如果报 Promise.withResolvers is not a function 请去查看版本兼容问题 降低pdf.js版本提高node版本 下载完成后 在 static 文件夹下新建 pdf 文件夹,将解压文件放进 pdf 文件…...
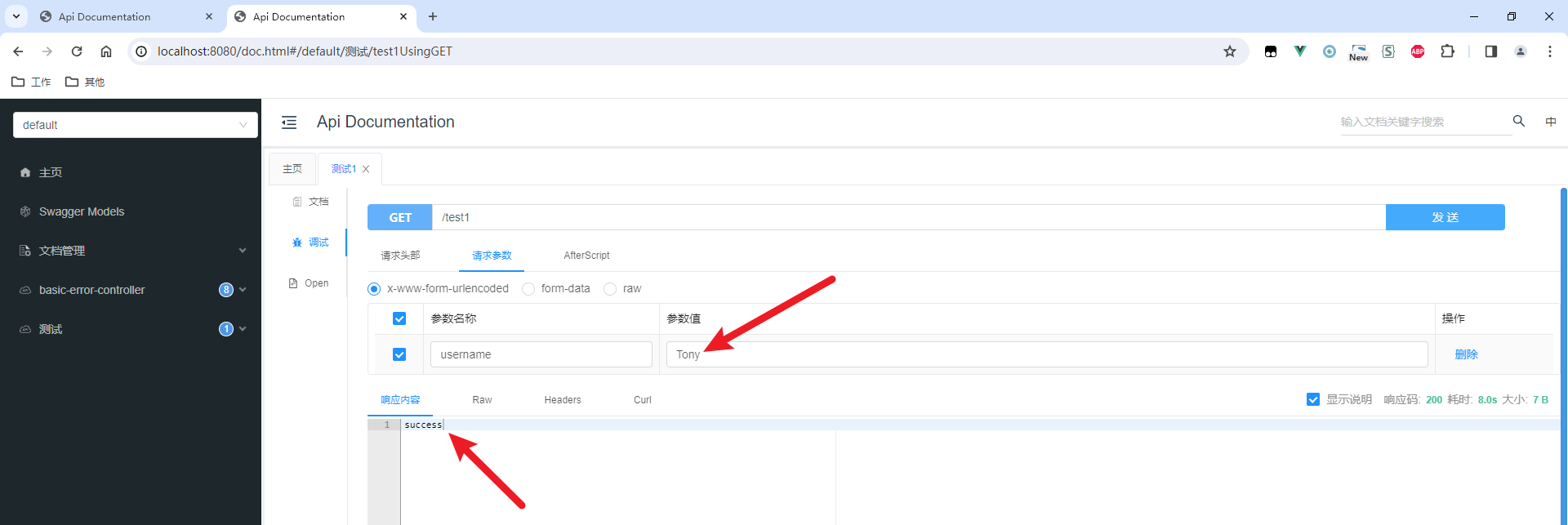
SpringBoot--为什么Controller是串行的?怎样才能并行?
原文网址:SpringBoot--为什么Controller是串行的?怎样才能并行?-CSDN博客 简介 本文介绍SpringBoot为什么Controller是串行的?在什么场景下才能并行执行? 大家都知道,SpringBoot的Controller按理是并行执…...
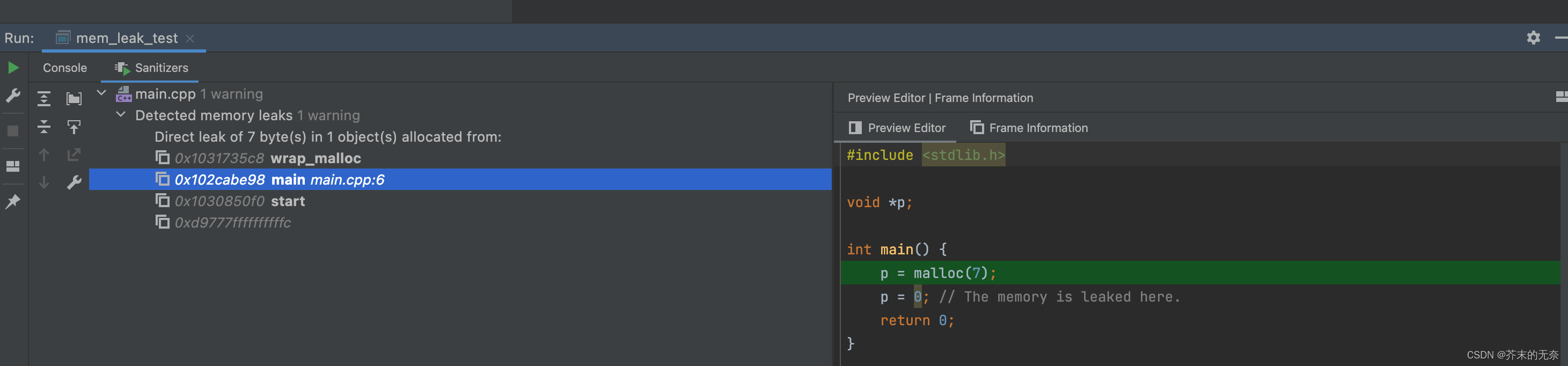
C/C++ 中的未定义行为(Undefined Behavior, UB)
0. 简介 在 C/C 编程中,理解未定义行为(UB)及其相关概念至关重要。本文将对未定义行为进行详细解析,并通过实例展示其影响与处理方法。 1. 概念辨析 在 C/C 中,未定义行为容易与以下两个概念混淆: 1.1 …...

AJAX 1——axios体验、认识URL、常用请求方法、HTTP协议、错误处理、form-serialize插件
AJAX 1——axios体验、认识URL、常用请求方法、HTTP协议、错误处理、form-serialize插件 1.AJAX入门与体验axios 定义:浏览器与服务器进行数据通信的技术 体验axios库,与服务器通信 引入axios.js使用axios函数 <p class"my-p"></p&…...
Java-运算符
一、运算符是什么? 其实就如字面意思一样啦~就像数学中的运算符一样:(" "," - "," * "," / "," % "...)。 计算机的用途就如其名:运算。而既然要运算…...
ubutun nginx 安装和解决端口占用问题
目录 一、删除已有nginx 二、安装nginx 三、端口占用问题 分析问题 解决方法:更换默认端口 nginx是一个高性能的 HTTP 和反向代理 web 服务器,同时也提供了 IMAP/POP3/SMTP 服务。是一款轻量级的 Web 服务器/反向代理服务器及电子邮件(I…...
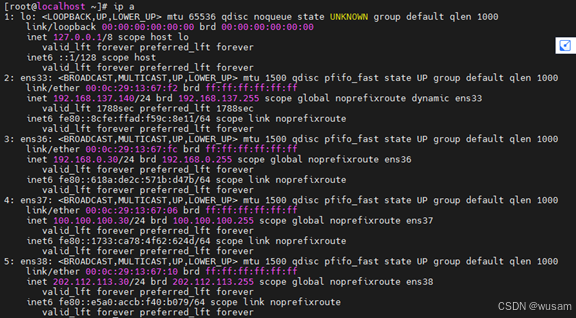
螺蛳壳里做道场:老破机搭建的私人数据中心---Centos下Docker学习01(环境准备)
1 准备工作 由于创建数据中心需要安装很多服务器,这些服务器要耗费很所物理物理计算资源、存储资源、网络资源和软件资源,作为穷学生只有几百块的n手笔记本,不可能买十几台服务器来搭建数据中心,也不愿意跑实验室,想躺…...
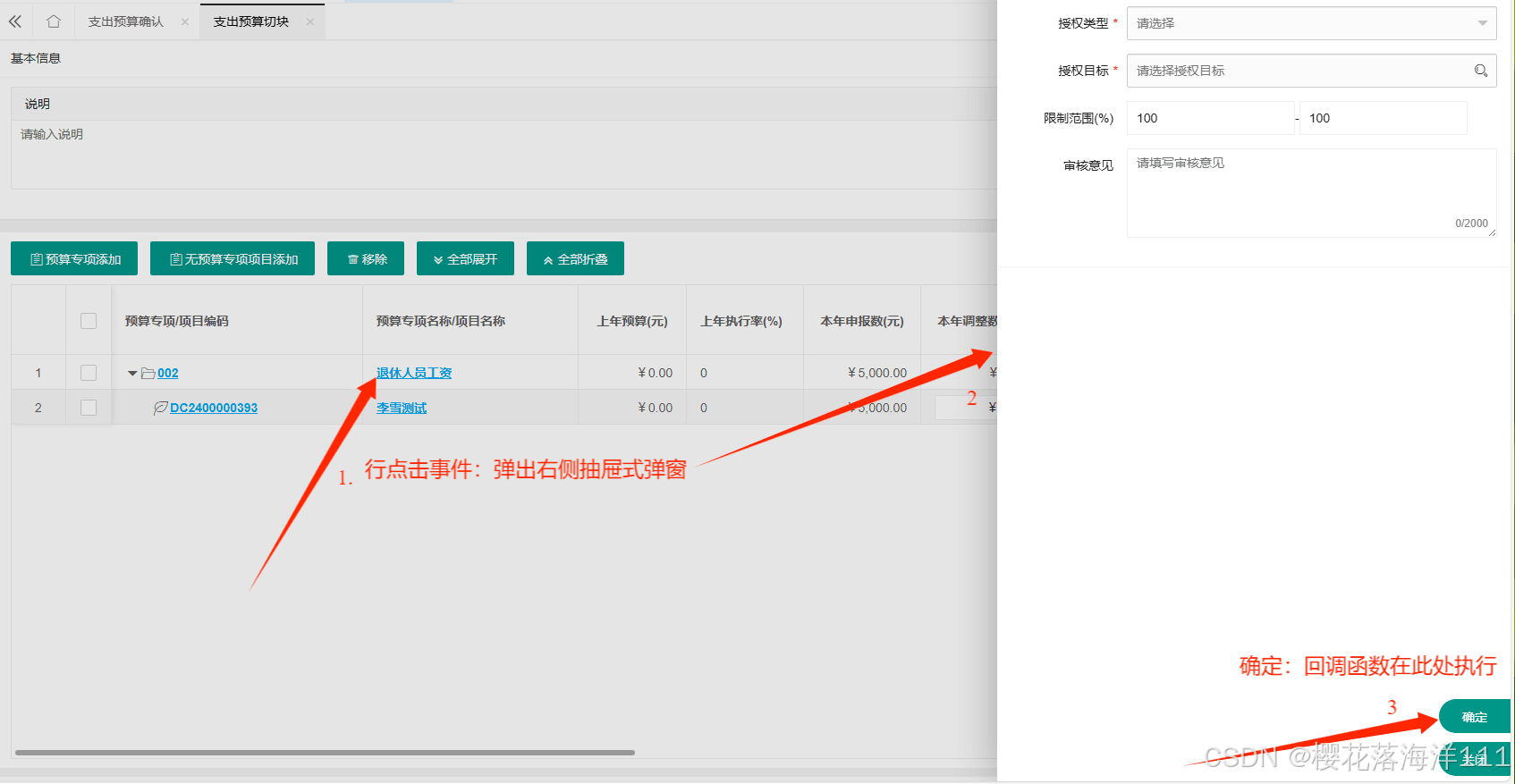
解决:使用layui.treeTable.updateNode,更新表格数据后,done里面的事件丢失问题
1. 背景 在给树形表格添加行点击事件,并且只更新当前行数据。 treeTable.updateNode("SpeProjListId", result.LAY_DATA_INDEX, result);更新数据后,点击事件失效。 1. 给字段绑定事件: class"link_a link_style" , {…...

【Linux】环境变量(初步认识环境变量)
文章目录 1. 环境变量1.1 基本概念 2. 认识常见环境变量2.1 PATH2.2 HOME2.3 SHELL2.4 PWD2.5 USER 3. 理解环境变量 1. 环境变量 在main函数的命令行参数中,有argc、argv、env三个参数。 argc:命令行参数的个数argc:存放每个参数的具体数值…...

79. 单词搜索
思路 每次以当前位置为初始位置开始遍历,看是否找到单词 (以官方题解做出) v:代表等于work[k]且已走过的位置 d:四个方向 回溯(遍历): 匹配不上:终止 找到了:终止(先…...
)
[单master节点k8s部署]28.Istio流量管理(四)
金丝雀发布实验 部署两个pod,他们分别是canary-v1和canary-v2。 随后进行service的部署: apiVersion: v1 kind: Service metadata:name: canary-svc34namespace: default spec:selector:apply: canaryports:- port: 80protocol: TCPtargetPort: 80进行…...

Windows 11 安装配置 Git 教程
目录 Git Windows 11 环境安装配置 Git Git Git是一个开源的分布式版本控制系统,由Linus Torvalds创建,用于有效、高速地处理从小到大的项目版本管理。Git是目前世界上最流行的版本控制系统,广泛应用于软件开发中。 以下是Git的一些关键特…...

Go基础学习11-测试工具gomock和monkey的使用
文章目录 基础回顾MockMock是什么安装gomockMock使用1. 创建user.go源文件2. 使用mockgen生成对应的Mock文件3. 使用mockgen命令生成后在对应包mock下可以查看生成的mock文件4. 编写测试代码5. 运行代码并查看输出 GomonkeyGomonkey优势安装使用对函数进行monkey对结构体中方法…...

PHP基础教程
PHP基础教程 1. PHP简介 PHP是一种广泛使用的开源服务器端脚本语言,它特别适用于网页开发,并可嵌入到HTML中使用。 2. PHP环境搭建 Windows: 可以使用XAMPP或WAMP。Mac: 可以使用MAMP。Linux: 可以使用XAMPP或LAMP。 3. 第一个PHP程序 创建一个名为…...

Python或R时偏移算法实现
🎯要点 计算单变量或多变量时序距离,使用欧几里得、曼哈顿等函数量化不同时序差异。量化生成时序之间接近度相似性矩阵。使用高尔距离和堪培拉距离等相似度测量。实现最小方差匹配算法,绘制步进模式的图形表示。其他语言包算法实现。 &…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
