市场中的新兴力量与未来发展
在当前瞬息万变的全球金融市场中,期货交易以其高杠杆与灵活性,吸引了越来越多的投资者参与其中。大粤期货作为中国期货行业的新兴力量,凭借其创新的交易平台、广泛的产品线及专业的风险管理服务,迅速在市场中崭露头角。本文将介绍大粤期货的优势、服务特色以及其对期货投资者的价值。
一、大粤期货的独特优势
-
全球化的市场视野
大粤期货不仅专注于国内市场,还积极参与国际期货交易,帮助客户开拓全球金融市场。通过其强大的全球网络,投资者可以轻松参与包括大宗商品、股指期货、外汇期货等在内的国际市场投资,享受更多元化的投资机会。 -
灵活的交易工具与创新技术
大粤期货依托现代化的技术,提供高度自动化的交易平台和个性化的交易工具。投资者不仅可以随时获取实时市场数据,还可以利用先进的技术分析工具进行深入的市场研判,帮助他们快速响应市场波动,做出及时的交易决策。 -
高效的风险管理体系
在期货交易中,风险管理尤为重要。大粤期货为投资者提供了多种风险管理工具,包括自动止损、对冲策略等。同时,公司会根据投资者的需求,提供定制化的风险控制方案,帮助他们在高风险市场中保护资本。
二、大粤期货的服务特色
大粤期货的客户服务体系以客户为中心,提供全天候的专业支持。不论投资者是新手还是经验丰富的交易者,都能在大粤期货找到适合的服务。公司定期举办线上培训和线下讲座,帮助投资者不断提升交易技巧,理解市场趋势。
此外,大粤期货还积极开发移动端交易平台,让投资者无论身处何地,都能轻松管理自己的投资组合,实现随时随地交易。
三、大粤期货的市场定位与未来发展
大粤期货定位于服务广泛的国内外客户群体,致力于为投资者提供多元化的期货产品和完善的投资方案。未来,公司将继续加大对金融科技的投入,提升客户的交易体验。同时,大粤期货将不断扩展其国际市场布局,力争成为全球投资者心目中的首选期货平台。
结语
随着期货市场的不断发展和国际化进程的加快,大粤期货为投资者提供了广泛的投资机会和专业的支持服务。凭借其先进的技术平台、丰富的产品线以及全面的风险管理体系,大粤期货正在帮助更多的投资者实现财富增长,并为期货市场的未来注入新的活力。
相关文章:

市场中的新兴力量与未来发展
在当前瞬息万变的全球金融市场中,期货交易以其高杠杆与灵活性,吸引了越来越多的投资者参与其中。大粤期货作为中国期货行业的新兴力量,凭借其创新的交易平台、广泛的产品线及专业的风险管理服务,迅速在市场中崭露头角。本文将介绍…...

Golang | Leetcode Golang题解之第446题等差数列划分II-子序列
题目: 题解: func numberOfArithmeticSlices(nums []int) (ans int) {f : make([]map[int]int, len(nums))for i, x : range nums {f[i] map[int]int{}for j, y : range nums[:i] {d : x - ycnt : f[j][d]ans cntf[i][d] cnt 1}}return }...

Java 常用序列化对比
Java 中常用的序列化方式主要包括以下几种: 1. Java 原生序列化 使用方式: 使用 java.io.Serializable 接口。对象需要实现该接口,然后通过 ObjectOutputStream 和 ObjectInputStream 进行序列化和反序列化。 示例代码: import java.io.*;public class Person impleme…...

【redis学习篇1】redis基本常用命令
目录 redis存储数据的模式 常用基本命令 一、set 二、keys pattern keys 字符串当中携带问号 keys 字符串当中携带*号 keys 【^字母】 keys * 三、exists 四、del 五、expire 5.1 ttl命令 5.2key删除策略 5.2.1惰性删除 5.2.2定期删除 六、type key的数据类型…...

量子计算:颠覆未来计算的革命性技术
量子计算:颠覆未来计算的革命性技术 量子计算作为下一代颠覆性技术,正在引领计算领域的重大变革。与传统计算机基于比特的二进制运算不同,量子计算通过量子比特(qubits)在叠加态和纠缠态下实现并行计算,能…...
ctfshow-web入门(信息收集,持续更新中。。)
写在之前:近期打了个比赛,备受打击,入手了vip账号进修,加油! 文章目录 ctfshow-web1查看源代码ctfshow-web2burp抓包ctfshow-web3burp抓包ctfshow-web4访问robots.txtctfshow-web5dirscarch扫描PHPS文件泄露ctfshow-web6dirscarch扫描ctfshow-web7dirscarch扫描ctfshow-w…...

蓝桥杯【物联网】零基础到国奖之路:十五. 扩展模块之双路ADC
蓝桥杯【物联网】零基础到国奖之路:十五. 扩展模块之双路ADC 第一节 硬件解读第二节 CubeMX配置第三节 代码编写 第一节 硬件解读 STM32的ADC是12位,通过硬件过采样扩展到16位,模数转换器嵌入到STM32L071xx器件中。有16个外部通道和2个内部通道…...

李飞飞谈AI+3D发展:3D/4D AI将成为下一个重要前沿
人工智能(AI)的发展已经深刻改变了我们的世界,从简单的图像识别到复杂的自然语言处理,再到如今正在兴起的生成式模型。在这个过程中,李飞飞教授认为,3D/4D AI技术将是推动下一波变革的关键力量。以下根据她的观点整理了AI发展历程中的关键里程碑以及对3D/4D AI未来发展的…...
centos72009源码编译R语言
./dev/make-distribution.sh --name custom-spark --pip --r --tgz -Pconnect -Psparkr -Phive -Phive-thriftserver -Pmesos -Pyarn -Dhadoop.version3.4.0 -Pkubernetes spark3.5.3 源码版本 ./dev/make-distribution.sh --name custom-spark --pip --r --tgz -Pconnect -P…...
初识算法 · 双指针(4)
目录 前言: 复写零 题目解析 算法原理 算法编写 四数之和 题目解析 算法原理 算法编写 前言: 本文是双指针算法的最后一文,以复写零和四数之和作为结束,介绍方式同样是题目解析,算法原理,算法编写…...

java版鸿鹄电子招投标系统功能架构设计 核心功能设计 鸿鹄电子招投标采购系统源码
java版鸿鹄电子招投标系统功能架构设计 核心功能设计 鸿鹄电子招投标采购系统源码...

matlab 判断多组数据的分布是否一致,可以使用什么方法?
在 MATLAB 中,可以使用以下几种方法来判断多组数据的分布是否一致: 1. Kolmogorov-Smirnov 检验 (K-S Test) K-S 检验是一种非参数检验,用于比较两组数据是否来自相同的分布。MATLAB 提供了 kstest2 函数来进行这种检验。该方法适用于连续分…...

jenkins配置eureka、nacos发布优雅上下线服务
eureka发布期间优雅上下线 1、编写eureka下线脚本 vim biz_out_of_service-eureka.pyimport sys import requests#服务名,脚本第一个参数 APP_NAMEsys.argv[1] # 需要置为OUT_OF_SERVICE的服务实例的ID,脚本第二个参数 INSTANCE_IDsys.argv[2]# Eureka…...

【JAVA开源】基于Vue和SpringBoot的周边产品销售网站
本文项目编号 T 061 ,文末自助获取源码 \color{red}{T061,文末自助获取源码} T061,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...

【C++差分数组】2381. 字母移位 II|1793
本文涉及知识点 C差分数组 LeetCode2381. 字母移位 II 给你一个小写英文字母组成的字符串 s 和一个二维整数数组 shifts ,其中 shifts[i] [starti, endi, directioni] 。对于每个 i ,将 s 中从下标 starti 到下标 endi (两者都包含&#…...

【pytorch】范数的计算
近日在看沐神的《动手学深度学习》,其中提到了范数这一数学概念,感觉很陌生,参考ChatGPT补一下知识。 目录 范数示例 1: 计算向量的 L2 范数(欧几里得范数)示例 2: 计算矩阵的 Frobenius 范数示例 3: 计算向量的 L1 范数(曼哈顿距离)曼哈顿范数的定义曼哈顿范数的计算示…...
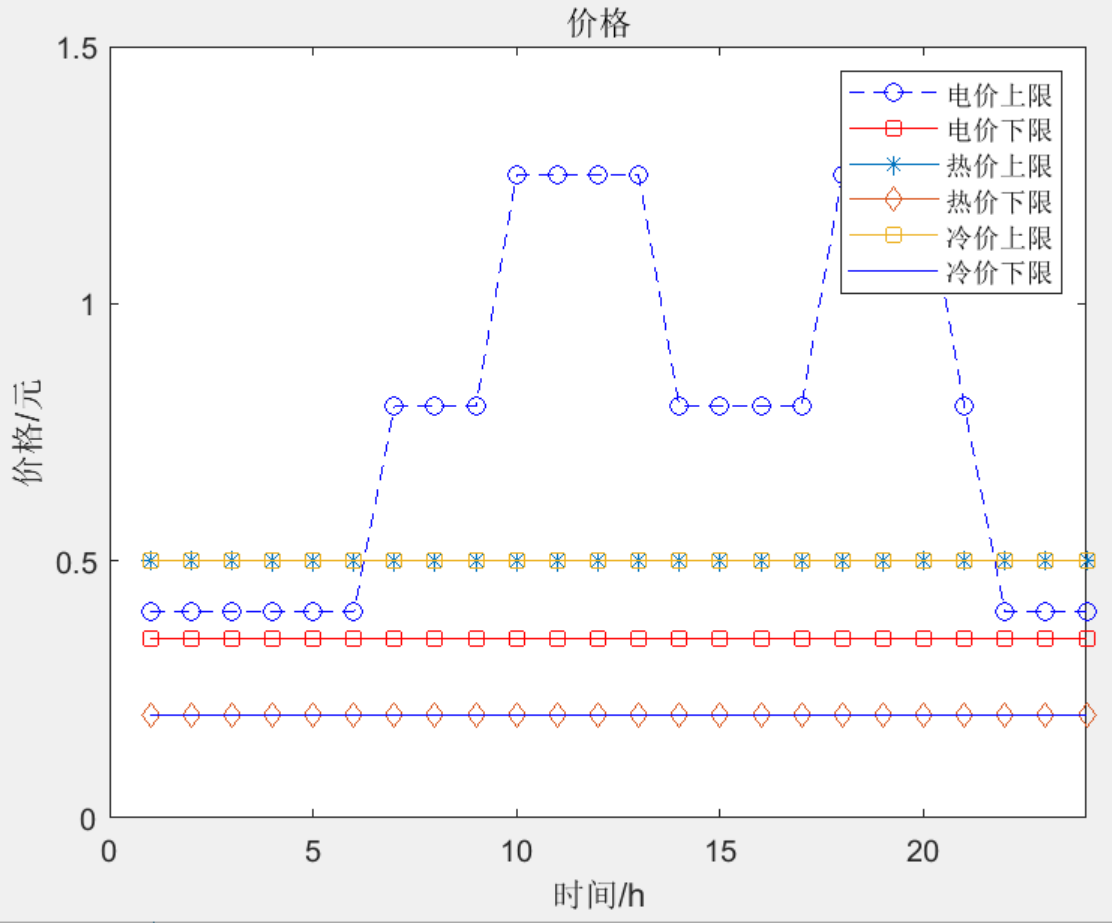
MATLAB|基于多主体主从博弈的区域综合能源系统低碳经济优化调度
目录 主要内容 程序亮点: 模型研究 一、综合能源模型 二、主从博弈框架 部分代码 结果一览 下载链接 主要内容 程序参考文献《基于多主体主从博弈的区域综合能源系统低碳经济优化调度》,采用了区域综合能源系统多主体博弈协同优化方…...
Django 后端数据传给前端
Step 1 创建一个数据库 Step 2 在Django中点击数据库连接 Step 3 连接成功 Step 4 settings中找DATABASES Step 5 将数据库挂上面 将数据库引擎和数据库名改成自己的 Step 6 在_init_.py中加上数据库的支持语句 import pymysql pymysql.install_as_MySQLdb() Step7 简单创建两…...
)
elasticsearch 写入新数据测试(二)
背景:elasticsearch单个node节点写入数据-CSDN博客 需要设置密码才能作为外部调用,不设置我不会用。设置方法见上一篇。 设置密码出现如下问题: Unexpected response code [503] from calling PUT http://172.19.0.1:9200/_security/user/apm_system/_password?pretty …...

android navigation 用法详细使用
Navigation 的关键概念 1、Navigation Graph: 定义了应用内的所有导航目的地以及它们之间的连接。 2、NavHost: 一个 UI 元素,用于承载当前的导航目的地。 3、NavController: 管理目的地之间的导航。 4、Destination: 导航图中的一个节点,用户导航到该节…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
