matlab 判断多组数据的分布是否一致,可以使用什么方法?
在 MATLAB 中,可以使用以下几种方法来判断多组数据的分布是否一致:
1. Kolmogorov-Smirnov 检验 (K-S Test)
K-S 检验是一种非参数检验,用于比较两组数据是否来自相同的分布。MATLAB 提供了 kstest2 函数来进行这种检验。该方法适用于连续分布的数据。
matlab
复制代码
[h, p] = kstest2(data1, data2);
h是检验结果,0 表示两组数据来自相同分布,1 表示不同分布。p是 p 值,如果小于显著性水平(通常是 0.05),则认为两组数据的分布显著不同。
2. Mann-Whitney U 检验 (也称为 Wilcoxon 秩和检验)
这是一个非参数检验,用于检验两组数据的分布是否相同。它不要求数据符合正态分布。MATLAB 可以通过 ranksum 函数进行此检验:
matlab
复制代码
[p, h] = ranksum(data1, data2);
p是 p 值,用于判断两组数据分布的相似性。h是检验结果,0 表示没有显著差异,1 表示有显著差异。
3. Chi-Square 检验 (卡方检验)
卡方检验通常用于分类数据来检验频率分布之间的差异。对于多组频率数据,可以使用 chi2gof 函数来进行适合度检验,比较实际观测频率与期望频率是否一致:
matlab
复制代码
[h, p] = chi2gof(data);
h是检验结果,0 表示没有显著差异,1 表示有显著差异。p是 p 值,表示分布是否相同。
4. Kruskal-Wallis 检验
Kruskal-Wallis 检验是一种非参数方法,用于比较多组数据的中位数是否相同。与 ANOVA 类似,但不要求数据服从正态分布。MATLAB 提供了 kruskalwallis 函数:
matlab
复制代码
p = kruskalwallis(data);
p是 p 值,判断组间是否有显著差异。
5. ANOVA 检验
如果数据符合正态分布,可以使用单因素方差分析(ANOVA)来检验多组数据的分布是否一致。MATLAB 中的 anova1 函数可以进行这种检验:
matlab
复制代码
p = anova1(data);
p是 p 值,判断各组之间是否有显著差异。
总结
- 对于连续数据,Kolmogorov-Smirnov 检验和 Mann-Whitney U 检验是常用的非参数方法。
- 对于分类数据或频率数据,Chi-Square 检验较为合适。
- 如果数据不符合正态分布,可以考虑 Kruskal-Wallis 检验。
- 数据服从正态分布时,ANOVA 是合适的选择。
这些方法可以根据不同数据特性和假设条件选择使用。
相关文章:

matlab 判断多组数据的分布是否一致,可以使用什么方法?
在 MATLAB 中,可以使用以下几种方法来判断多组数据的分布是否一致: 1. Kolmogorov-Smirnov 检验 (K-S Test) K-S 检验是一种非参数检验,用于比较两组数据是否来自相同的分布。MATLAB 提供了 kstest2 函数来进行这种检验。该方法适用于连续分…...

jenkins配置eureka、nacos发布优雅上下线服务
eureka发布期间优雅上下线 1、编写eureka下线脚本 vim biz_out_of_service-eureka.pyimport sys import requests#服务名,脚本第一个参数 APP_NAMEsys.argv[1] # 需要置为OUT_OF_SERVICE的服务实例的ID,脚本第二个参数 INSTANCE_IDsys.argv[2]# Eureka…...

【JAVA开源】基于Vue和SpringBoot的周边产品销售网站
本文项目编号 T 061 ,文末自助获取源码 \color{red}{T061,文末自助获取源码} T061,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...

【C++差分数组】2381. 字母移位 II|1793
本文涉及知识点 C差分数组 LeetCode2381. 字母移位 II 给你一个小写英文字母组成的字符串 s 和一个二维整数数组 shifts ,其中 shifts[i] [starti, endi, directioni] 。对于每个 i ,将 s 中从下标 starti 到下标 endi (两者都包含&#…...

【pytorch】范数的计算
近日在看沐神的《动手学深度学习》,其中提到了范数这一数学概念,感觉很陌生,参考ChatGPT补一下知识。 目录 范数示例 1: 计算向量的 L2 范数(欧几里得范数)示例 2: 计算矩阵的 Frobenius 范数示例 3: 计算向量的 L1 范数(曼哈顿距离)曼哈顿范数的定义曼哈顿范数的计算示…...
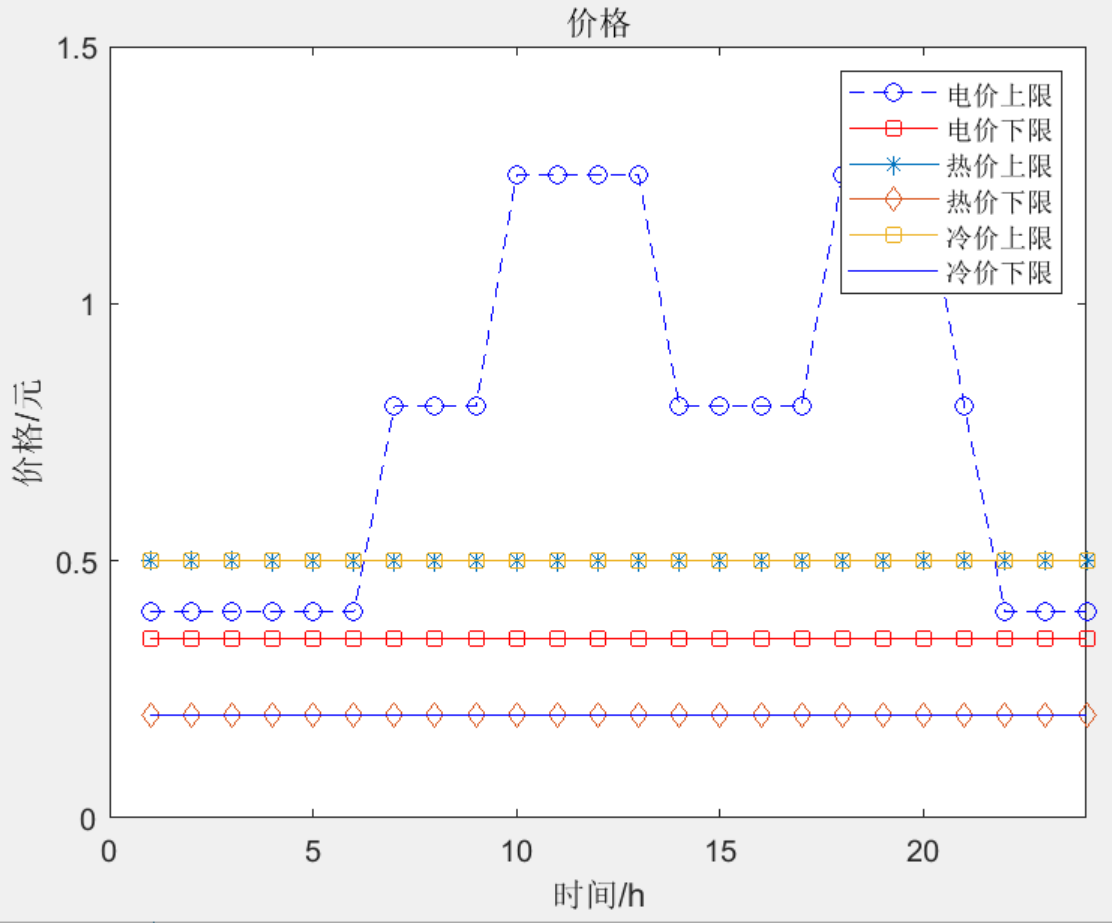
MATLAB|基于多主体主从博弈的区域综合能源系统低碳经济优化调度
目录 主要内容 程序亮点: 模型研究 一、综合能源模型 二、主从博弈框架 部分代码 结果一览 下载链接 主要内容 程序参考文献《基于多主体主从博弈的区域综合能源系统低碳经济优化调度》,采用了区域综合能源系统多主体博弈协同优化方…...
Django 后端数据传给前端
Step 1 创建一个数据库 Step 2 在Django中点击数据库连接 Step 3 连接成功 Step 4 settings中找DATABASES Step 5 将数据库挂上面 将数据库引擎和数据库名改成自己的 Step 6 在_init_.py中加上数据库的支持语句 import pymysql pymysql.install_as_MySQLdb() Step7 简单创建两…...
)
elasticsearch 写入新数据测试(二)
背景:elasticsearch单个node节点写入数据-CSDN博客 需要设置密码才能作为外部调用,不设置我不会用。设置方法见上一篇。 设置密码出现如下问题: Unexpected response code [503] from calling PUT http://172.19.0.1:9200/_security/user/apm_system/_password?pretty …...

android navigation 用法详细使用
Navigation 的关键概念 1、Navigation Graph: 定义了应用内的所有导航目的地以及它们之间的连接。 2、NavHost: 一个 UI 元素,用于承载当前的导航目的地。 3、NavController: 管理目的地之间的导航。 4、Destination: 导航图中的一个节点,用户导航到该节…...

uni-app在线预览pdf
这里推荐下载pdf.js 插件 PDF.js - Browse Files at SourceForge.net 特此注意 如果报 Promise.withResolvers is not a function 请去查看版本兼容问题 降低pdf.js版本提高node版本 下载完成后 在 static 文件夹下新建 pdf 文件夹,将解压文件放进 pdf 文件…...
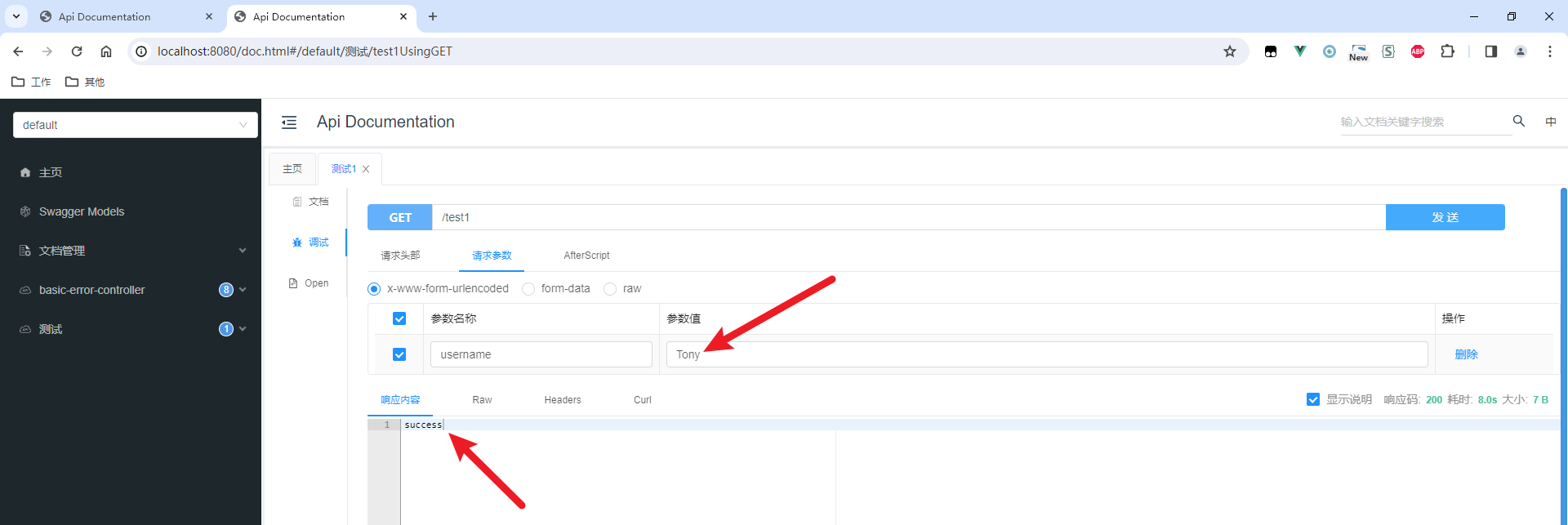
SpringBoot--为什么Controller是串行的?怎样才能并行?
原文网址:SpringBoot--为什么Controller是串行的?怎样才能并行?-CSDN博客 简介 本文介绍SpringBoot为什么Controller是串行的?在什么场景下才能并行执行? 大家都知道,SpringBoot的Controller按理是并行执…...
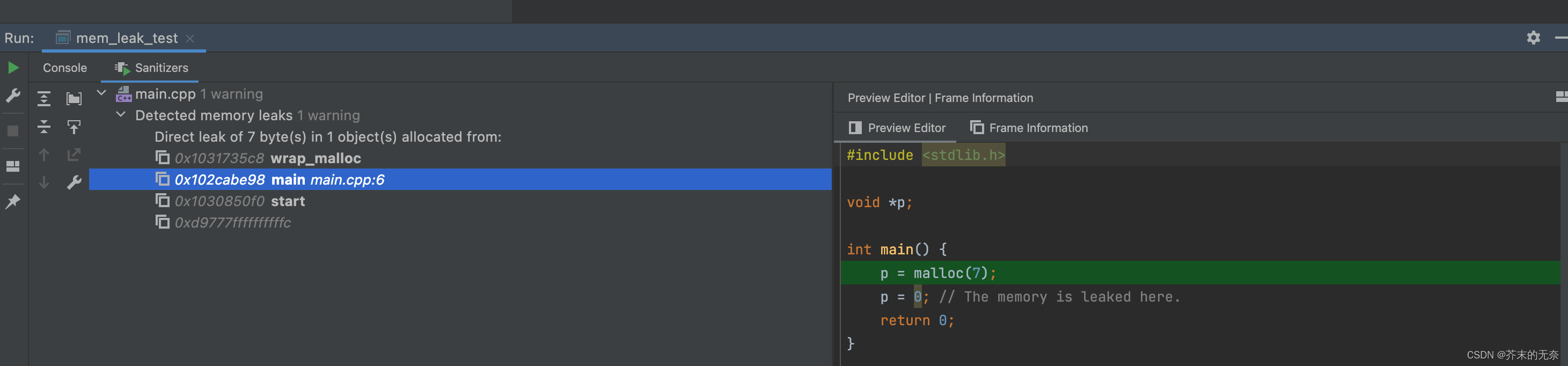
C/C++ 中的未定义行为(Undefined Behavior, UB)
0. 简介 在 C/C 编程中,理解未定义行为(UB)及其相关概念至关重要。本文将对未定义行为进行详细解析,并通过实例展示其影响与处理方法。 1. 概念辨析 在 C/C 中,未定义行为容易与以下两个概念混淆: 1.1 …...

AJAX 1——axios体验、认识URL、常用请求方法、HTTP协议、错误处理、form-serialize插件
AJAX 1——axios体验、认识URL、常用请求方法、HTTP协议、错误处理、form-serialize插件 1.AJAX入门与体验axios 定义:浏览器与服务器进行数据通信的技术 体验axios库,与服务器通信 引入axios.js使用axios函数 <p class"my-p"></p&…...
Java-运算符
一、运算符是什么? 其实就如字面意思一样啦~就像数学中的运算符一样:(" "," - "," * "," / "," % "...)。 计算机的用途就如其名:运算。而既然要运算…...
ubutun nginx 安装和解决端口占用问题
目录 一、删除已有nginx 二、安装nginx 三、端口占用问题 分析问题 解决方法:更换默认端口 nginx是一个高性能的 HTTP 和反向代理 web 服务器,同时也提供了 IMAP/POP3/SMTP 服务。是一款轻量级的 Web 服务器/反向代理服务器及电子邮件(I…...
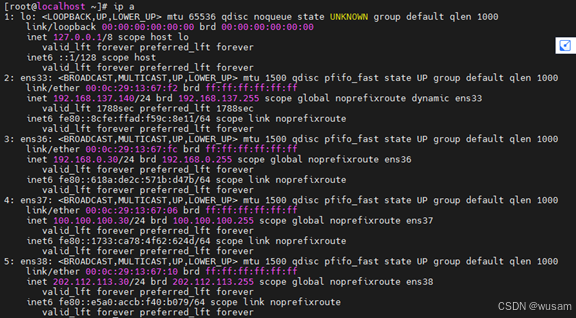
螺蛳壳里做道场:老破机搭建的私人数据中心---Centos下Docker学习01(环境准备)
1 准备工作 由于创建数据中心需要安装很多服务器,这些服务器要耗费很所物理物理计算资源、存储资源、网络资源和软件资源,作为穷学生只有几百块的n手笔记本,不可能买十几台服务器来搭建数据中心,也不愿意跑实验室,想躺…...
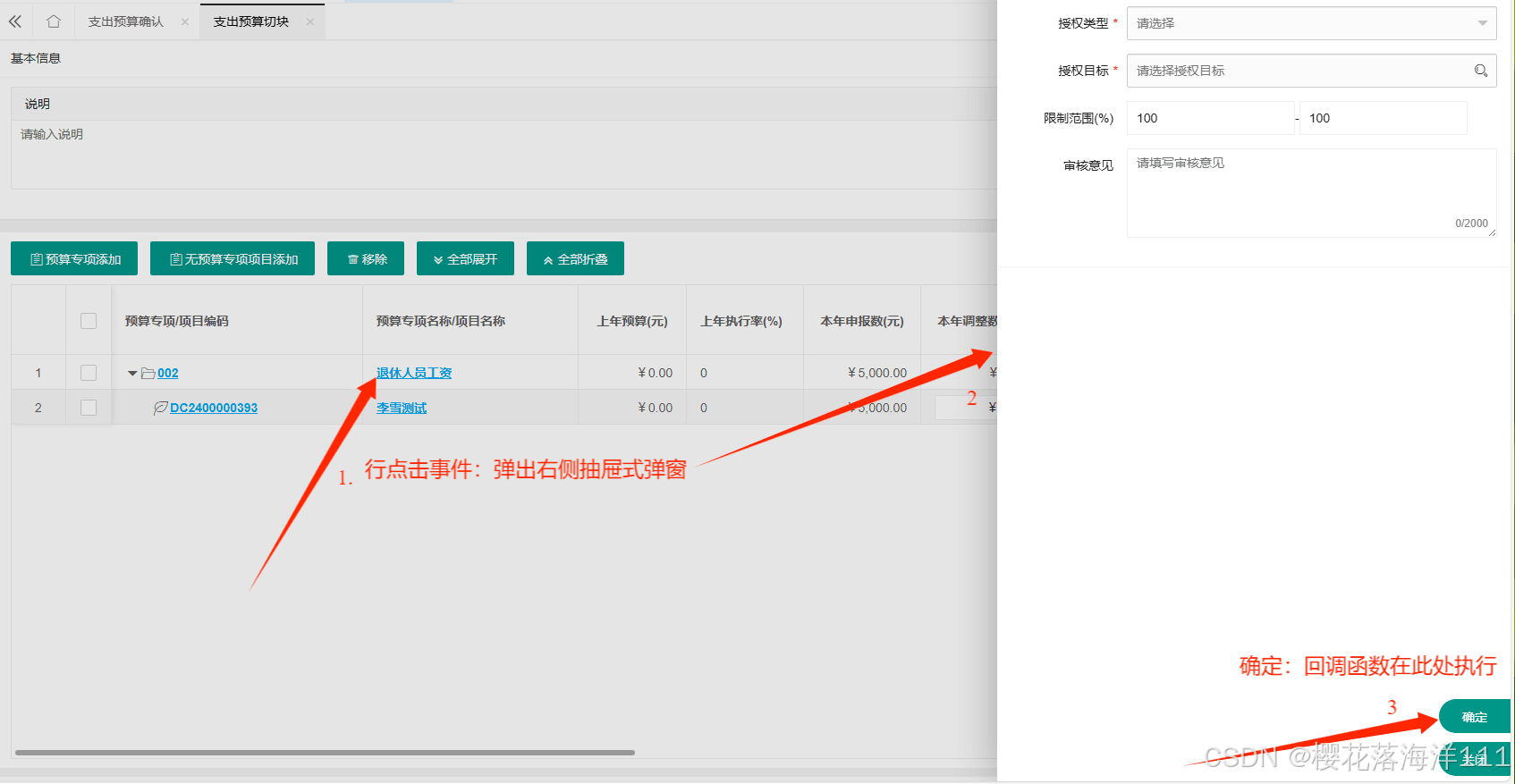
解决:使用layui.treeTable.updateNode,更新表格数据后,done里面的事件丢失问题
1. 背景 在给树形表格添加行点击事件,并且只更新当前行数据。 treeTable.updateNode("SpeProjListId", result.LAY_DATA_INDEX, result);更新数据后,点击事件失效。 1. 给字段绑定事件: class"link_a link_style" , {…...

【Linux】环境变量(初步认识环境变量)
文章目录 1. 环境变量1.1 基本概念 2. 认识常见环境变量2.1 PATH2.2 HOME2.3 SHELL2.4 PWD2.5 USER 3. 理解环境变量 1. 环境变量 在main函数的命令行参数中,有argc、argv、env三个参数。 argc:命令行参数的个数argc:存放每个参数的具体数值…...

79. 单词搜索
思路 每次以当前位置为初始位置开始遍历,看是否找到单词 (以官方题解做出) v:代表等于work[k]且已走过的位置 d:四个方向 回溯(遍历): 匹配不上:终止 找到了:终止(先…...
)
[单master节点k8s部署]28.Istio流量管理(四)
金丝雀发布实验 部署两个pod,他们分别是canary-v1和canary-v2。 随后进行service的部署: apiVersion: v1 kind: Service metadata:name: canary-svc34namespace: default spec:selector:apply: canaryports:- port: 80protocol: TCPtargetPort: 80进行…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
