随想录Day45--动态规划:70. 爬楼梯 (进阶), 322. 零钱兑换, 279.完全平方数
70爬楼梯这道题之前已经做过,是动态规划思想的入门,想要爬上第n层阶梯,看爬上n-1层的方法和n-2层的方法共有多少种,两个相加就是爬上n层阶梯的方法。这里扩展到每次可以爬k层,这样就是一个动态规划问题。因为每次可以爬1-k层,所以把k作为物品,爬到n层作为背包容量,爬的楼梯数k可以重复,所以是个完全背包问题。定义数组dp[i],dp[i]表示爬上i层阶梯的方法数。初始化dp[0]= 1,因为爬上第0层的方法为1,也就是不用动。因为爬楼梯的层数可以重复,所以我理解成排列问题,遍历顺序先背包容量再物品,物品再内层循环,每次就都可以从最小开始,可以重复。
322零钱兑换,目标数是背包容量,零钱数组coins是物品,dp[i]表示的是零钱的个数。初始化dp[0] = 0,因为0元的兑换不需要硬币,所以是0.因为零钱是可以重复使用的,所以是个完全背包问题,但是零钱是个组合问题,比如说6块钱可以用5元和1元零钱兑换,也可以用1元和5元兑换(和5元,1元的顺序不同),但是是同一种方法,所以这是组合问题。组合问题要先遍历物品再遍历背包。
79完全平方数,整数n时背包容量,物品是完全平方数,dp[i]表示和为n的最小物品数量。这里完全平方数可以重复使用,并且是个组合问题,和完全平方数的顺序无关,所以是个多重背包的组合问题。需要先遍历物品,再遍历背包容量。
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示:
1 <= n <= 45
class Solution {public int climbStairs(int n) {// int [] dp = new int[3];// if(n < 3){// return n;// }// dp[0] = 1;// dp[1] = 2;// for(int i = 2; i < n; i++){// dp[2] = dp[1] + dp[0];// dp[0] = dp[1];// dp[1] = dp[2];// }// return dp[2];int[] dp = new int[n + 1];int[] weigh = {1, 2};dp[0] = 1;for(int i = 0; i <= n; i++){for(int j = 0; j < weigh.length; j++){if(i >= weigh[j]){dp[i] += dp[i - weigh[j]];}}}return dp[n];}
}322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1
示例 2:
输入:coins =[2], amount =3输出:-1
示例 3:
输入:coins = [1], amount = 0 输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
class Solution {public int coinChange(int[] coins, int amount) {int len = coins.length;int[] dp = new int[amount + 1];dp[0] = 0;for(int i = 1; i <= amount; i++){dp[i] = amount + 1;}for(int i = 0; i < len; i++){for(int j = coins[i]; j <= amount; j++){dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}if(dp[amount] > amount){return -1;}return dp[amount];}
}279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n =12输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n =13输出:2 解释:13 = 4 + 9
提示:
1 <= n <= 104
class Solution {public int numSquares(int n) {int[] dp = new int[n + 1];for(int i = 0; i <= n; i++){dp[i] = n;}dp[0] = 0;for(int i = 1; i * i <= n ; i++){for(int j = i * i; j <= n; j++){dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
}相关文章:
, 322. 零钱兑换, 279.完全平方数)
随想录Day45--动态规划:70. 爬楼梯 (进阶), 322. 零钱兑换, 279.完全平方数
70爬楼梯这道题之前已经做过,是动态规划思想的入门,想要爬上第n层阶梯,看爬上n-1层的方法和n-2层的方法共有多少种,两个相加就是爬上n层阶梯的方法。这里扩展到每次可以爬k层,这样就是一个动态规划问题。因为每次可以爬…...

原理+案例,关于主从延迟,一篇文章给你讲明白!
前言 在生产环境中,为了满足安全性,高可用性以及高并发等方面的需求,基本上采用的MySQL数据库架构都是MHA、MGR等,最低也得是一主一从的架构,搭配自动切换脚本,实现故障自动切换。 上述架构都是通过集群主…...
QT开发笔记(Camera)
Camera 此章节例程适用于 Ubuntu 和正点原子 I.MX6U 开发板,不适用于 Windows(需要自行修改 才能适用 Windows,Windows 上的应用不在我们讨论范围)! 资源简介 正点原子 I.MX6U 开发板底板上有一路“CSI”摄像头接口。支持正点原…...
从C++的角度讲解C#容器
讲解C#容器的文章网上一搜一大把,作为一名C程序员如何高效学习C#容器呢,其实学语言如果能讲到这点就能触类旁通,举一反三,那效果是最好的问题市面上没有这样的书籍,那就跟着老白来一起从C的角度去讲解C#容器1.List<…...

React组件库实践:React + Typescript + Less + Rollup + Storybook
背景 原先在做低代码平台的时候,刚好有搭载React组件库的需求,所以就搞了一套通用的React组件库模版。目前通过这套模板也搭建过好几个组件库。 为了让这个模板更干净和通用,我把所有和低代码相关的代码都剔除了,只保留最纯粹的…...

c++ atomic
文章目录why atomic?sequentially consistent atomicRelaxed memory modelswhy atomic? 当我们有一片内存空间S,线程A正在往S里写数据,这个时候线程B突然往S中做了操作,导致线程A的操作结果变得不可预知(对线程A来说),这种情况换句话说叫做data race,我们一般的操作时上锁,在…...
要想孩子写作文没烦恼?建议家长这样做
说起语文学习,就不得不提作文。作为语文学习中的重中之重,作文写作一直是压在学生和家长身上的一块“心头大石”。发现很多孩子在写作文时,往往存在四大问题:写不出、不生动、流水账、太空洞。如今,孩子怕写作文&#…...
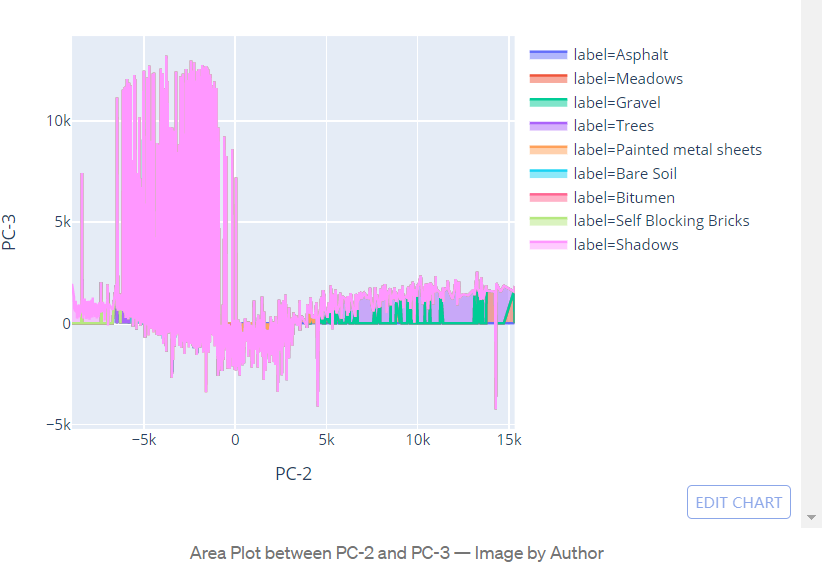
基于Python的高光谱图像分析教程
1、前言超光谱图像 (HSI) 分析因其在从农业到监控的各个领域的应用而成为人工智能 (AI) 研究的前沿领域之一。 该领域正在发表许多研究论文,这使它变得更加有趣! 和“对于初学者来说,在 HSI 上开始模式识别和机器学习是相当麻烦的”ÿ…...

【图神经网络】从0到1使用PyG手把手创建异构图
从0到1用PyG创建异构图异构图创建异构图电影评分数据集MovieLens建立二分图数据集转换为可训练的数据集建立异构图神经网络以OGB数据集为例HeteroData中常用的函数将简单图神经网络转换为异质图神经网络GraphGym的使用PyG中常用的卷积层参考资料在现实中需要对 多种类型的节点以…...
2023美赛春季赛思路分析汇总
将在本帖更新汇总2023美赛春季赛两个赛题思路,大家可以点赞收藏! 2023美赛春季赛各赛题全部解题参考思路资料模型代码等全部实时更新!第一时间获取全部美赛春季赛相关资料! 目前思路整理仅为部分,请大家耐心等待&…...
GPT4国内镜像站
GPT-4介绍GPT-4是OpenAI发布的最先进的大型语言模型,是ChatGPT模型的超级进化版本。与ChatGPT相比,GPT-4的推理能力、复杂问题的理解能力、写代码能力得到了极大的强化,是当前人工智能领域,最有希望实现通用人工智能的大模型。但G…...

代码随想录算法训练营第四十八天| 198 打家劫舍 213 打家劫舍II 337 打家劫舍III
代码随想录算法训练营第四十八天| 198 打家劫舍 213 打家劫舍II 337 打家劫舍III LeetCode 198 打家劫舍 题目: 198.打家劫舍 动规五部曲: 确定dp数组以及下标的含义 dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷…...
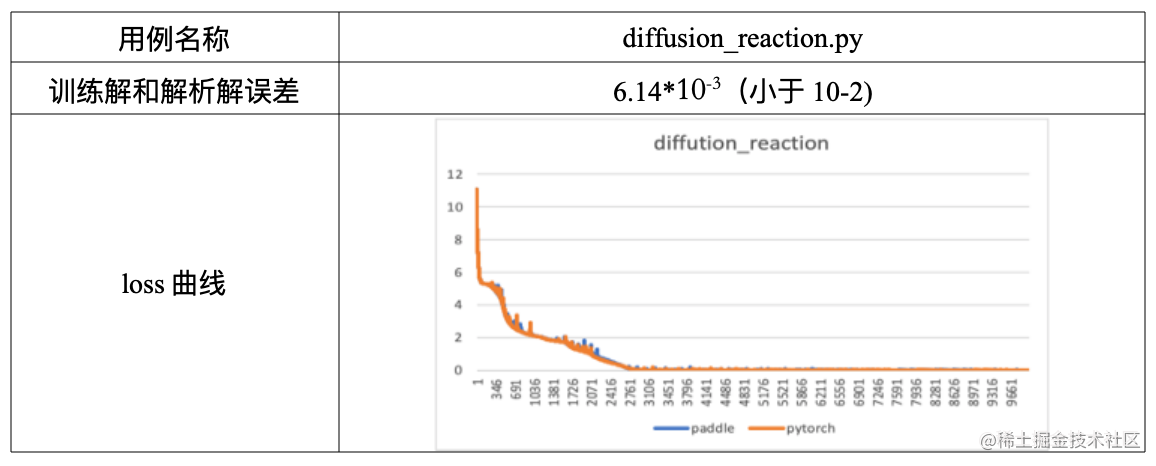
飞桨DeepXDE用例验证及评估
在之前发布的文章中,我们介绍了飞桨全量支持业内优秀科学计算深度学习工具 DeepXDE。本期主要介绍基于飞桨动态图模式对 DeepXDE 中 PINN 方法用例实现、验证及评估的具体流程,同时提供典型环节的代码,旨在帮助大家更加高效地基于飞桨框架进行…...

telegram连接本地Proxy连接不上
1.ClashX开启允许局域网连接。 2.重启ClashX和Telegram...
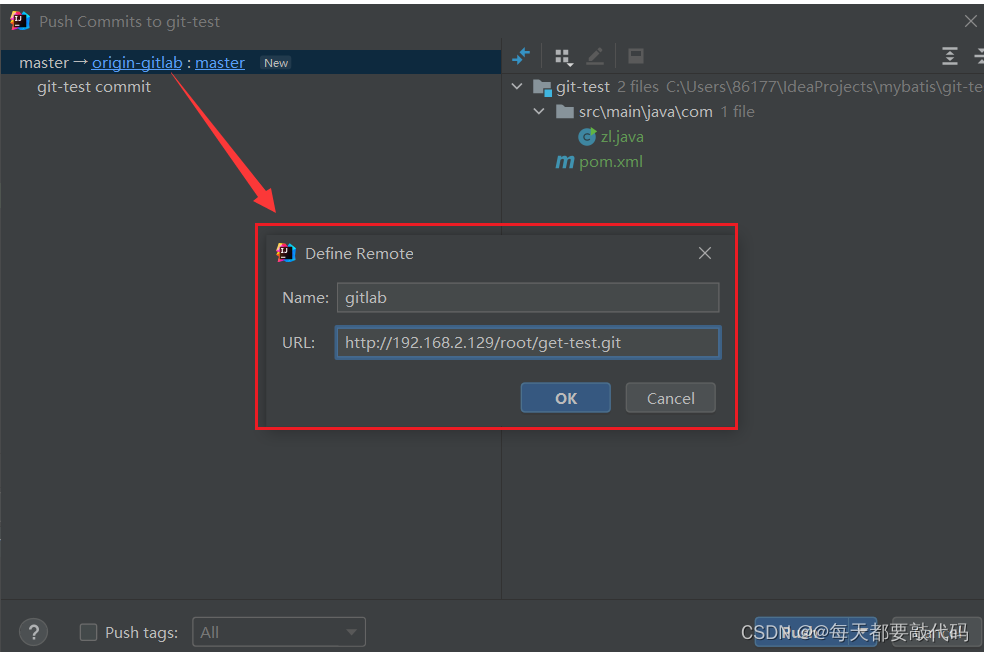
【分布式版本控制系统Git】| 国内代码托管中心-Gitee、自建代码托管平台-GitLab
目录 一:国内代码托管中心-码云 1. 码云创建远程库 2. IDEA 集成码云 3. 码云复制 GitHub 项目 二:自建代码托管平台-GitLab 1. GitLab 安装 2. IDEA 集成 GitLab 一:国内代码托管中心-码云 众所周知,GitHub 服务器在国外&…...
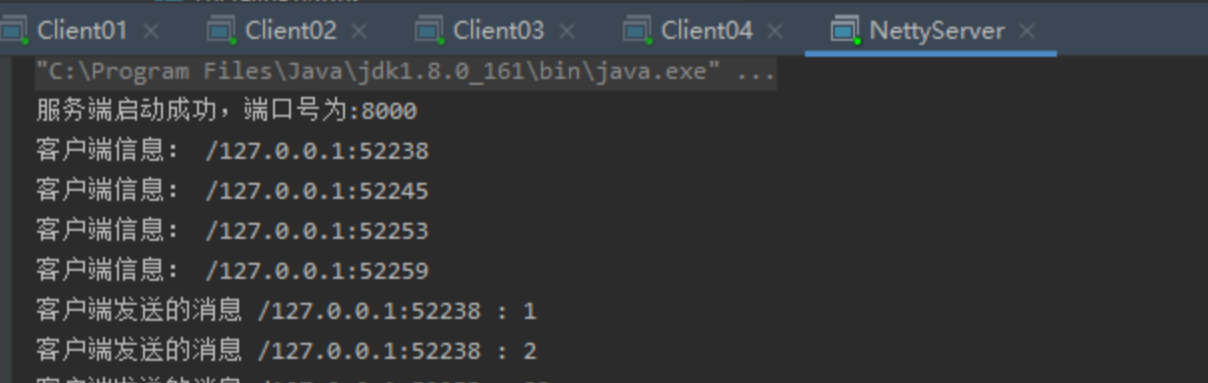
【面试】BIO、NIO、AIO面试题
文章目录什么是IO在了解不同的IO之前先了解:同步与异步,阻塞与非阻塞的区别什么是BIO什么是NIO什么是AIO什么NettyBIO和NIO、AIO的区别IO流的分类按照读写的单位大小来分:按照实际IO操作来分:按照读写时是否直接与硬盘,…...

C语言实现拼图求解
题目: 有如下的八种拼图块,每块都是由八块小正方块构成, 这些拼图块刚好可以某种方式拼合放入给定的目标形状, 请以C或C++编程,自动求解 一种拼图方式 目标拼图: 本栏目适合想要深入了解无向图、深度优先算法、编程语句如何实现算法、想要去接拼图算法的小伙伴。...

python --获取本机屏幕分辨率
pywin32 方法一 使用 win32api.GetDeviceCaps() 方法来获取显示器的分辨率。 使用 win32api.GetDC() 方法获取整个屏幕的设备上下文句柄,然后使用 win32api.GetDeviceCaps() 方法获取水平和垂直方向的分辨率。最后需要调用 win32api.ReleaseDC() 方法释放设备上下…...
Java多态
目录 1.多态是什么? 2.多态的条件 3.重写 3.1重写的概念 3.2重写的作用 3.3重写的规则 4.向上转型与向下转型 4.1向上转型 4.2向下转型 5.多态的优缺点 5.1 优点 5.2 缺点 面向对象程序三大特性:封装、继承、多态。 1.多态是什么࿱…...

绝对路径和相对路径
1.绝对路径:从根目录为起点到某一个目录的路径 使用计算机时要找到需要的文件就必须知道文件的位置,表示文件的位置的方式就是路径,例如只要看到这个路径:c:/website/img/photo.jpg我们就知道photo.jpg文件是在c盘的website目录下…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
