双指针:滑动窗口
题目描述
- 给定两个字符串 S 和 T,求 S 中包含 T 所有字符的最短连续子字符串的长度,同时要求时间复杂度不得超过 O(n)。
输入输出样例
- 输入是两个字符串 S 和 T,输出是一个 S 字符串的子串。样例如下:
在这个样例中, S 中同时包含一个 A、一个 B、一个 C 的最短子字符串是“BANC”。
| Input: S = “ADOBECODEBANC”, T = “ABC” Output: “BANC” |
|---|
算法步骤
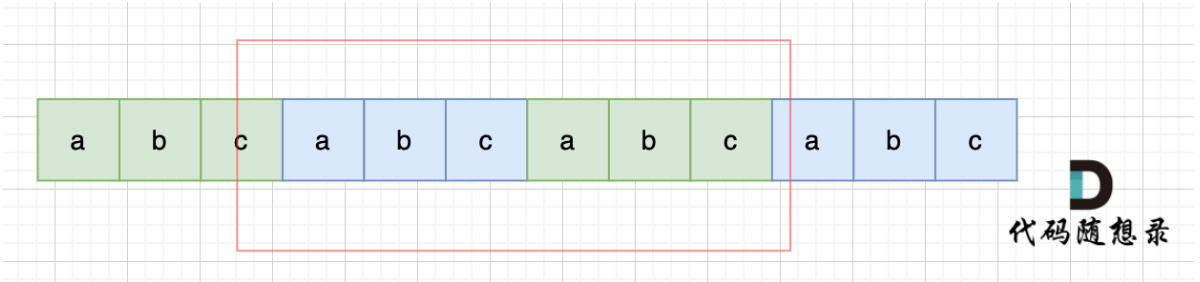
- 本题使用滑动窗口求解,即两个指针 l 和 r 都是从最左端向最右端移动,且 l 的位置一定在 r 的左边或重合。注意本题虽然在 for 循环里出现了一个 while 循环,但是因为 while 循环负责移动 l 指针,且 l 只会从左到右移动一次,因此总时间复杂度仍然是 O(n)。
- 先统计 T 中的各字符是否出现及数量,用 flag[i]代表代表ACII值为i的字符是否出现, chars [i] 表示ACII值为i的字符在T中出现的次数,也可以用于表示当前窗口中缺少的字符的数量。
- cnt 表示当前窗口中的 包含T中字符 的数量,由于后续代码中 cnt 的变化都和 chars 有关(每次chars 变化后,cnt才变换),则可直接用 cnt 的值和 T的大小比较,判断滑动窗口中是否都包含了T中的字符。左指针 l 和右指针 r 开始默认指向字符串最左边的第一个元素。初始化滑动窗口的最小值为整个S的长度+1,即表示整个S字符串都不匹配。
- 接下来的 for 外层循环 负责移动窗口的 右指针r 来遍历字符串 S,若 S[r] 不是T中的字符,则不做处理, r 往右遍历;若 S[r] 是T中的字符,则进行以下处理:
- 判断 当前窗口中是否还缺少字符 S[r] ,若缺少,则 cnt++。
- 若 cnt 的值等于 T 的大小,则表示当前滑动窗口中已经包含了 T 中所有字符,然后进入while 内层循环,负责移动左指针 l:将 左指针l 右移,在不影响结果的情况收缩窗口,以获得最短子字符串。
- 若当前滑窗长度 < 最小长度,则刷新最小长度和左指针 l。
- 若 左指针指向的字符 S[l] 属于T中的字符,且++chars[S[l]] > 0即左指针再往后移的话滑动窗口就不再满足条件,表示此时已是 当前 r 遍历条件下的最小窗口,然后将 cnt-- 表示后续将 l 右移一步的话,滑动窗口内T中的字符数量将少1。
- 左指针 l 继续右移一步向后遍历。
- 最后判断滑动窗口的长度,若大于S的长度表示整个S都不匹配返回空,否则进行切片处理返回字符串S中左指针和右指针所截取的窗口内容。
PS:为什么左指针只需要从左到右 右移一次即可,不需要在每次 右指针r 遍历的情况下将左指针从左到右重新右移一遍?
答:在 r 时,遍历到的最小滑窗窗口比如说 [l,p] ,长度是 p-l+1,r≥p。
在 r+1 时,若想要遍历到更小的窗口,则滑动窗口的左指针只能继续往后移,因为前面已经确定最小的滑动窗口。
#include <iostream>
#include <vector>
using namespace std;
string minWindow(string S, string T) {vector<int> chars(128, 0); // ASCII表共128个字符,chars[i]代表ACII值为i的字符在T中出现的次数vector<bool> flag(128, false); // flag[i]代表代表ACII值为i的字符是否出现// 先统计T中的字符情况for (int i = 0; i < T.size(); ++i) {flag[T[i]] = true;++chars[T[i]];}// 移动滑动窗口, 不断更改统计数据int cnt = 0, l = 0, min_l = 0, min_size = S.size() + 1;for (int r = 0; r < S.size(); ++r) { //接下来的外层循环通过移动窗口的右边界r来遍历字符串S。if (flag[S[r]]) { //若S[r]是T中的字符if (--chars[S[r]] >= 0) { //若当前窗口中还缺该字符,则cnt++++cnt;}// 若目前滑动窗口已包含T中全部字符,// 则尝试将l右移, 在不影响结果的情况下获得最短子字符串while (cnt == T.size()) {if (r - l + 1 < min_size) { // 当前滑窗长度 < 最小长度min_l = l;min_size = r - l + 1;}if (flag[S[l]] && ++chars[S[l]] > 0) { // 当前l缩进的窗口已经最小,不再满足条件cnt--;}++l; //左指针右移}}}return min_size > S.size() ? "" : S.substr(min_l, min_size);
}int main() {string S = "ADOBECODEBANC", T = "ABC";cout << minWindow(S,T);return 0;
}

相关文章:

双指针:滑动窗口
题目描述 给定两个字符串 S 和 T,求 S 中包含 T 所有字符的最短连续子字符串的长度,同时要求时间复杂度不得超过 O(n)。 输入输出样例 输入是两个字符串 S 和 T,输出是一个 S 字符串的子串。样例如下: 在这个样例中,…...

云原生(四十八) | Nginx软件安装部署
文章目录 Nginx软件安装部署 一、Nginx软件部署步骤 二、安装与配置Nginx Nginx软件安装部署 一、Nginx软件部署步骤 第一步:安装 Nginx 软件 第二步:把 Nginx 服务添加到开机启动项 第三步:配置 Nginx 第四步:启动Nginx …...

【WPF开发】如何设置窗口背景颜色以及背景图片
在WPF中,可以通过设置窗口的 Background 属性来改变窗口的背景。以下是一些设置窗口背景的不同方法: 一、设置纯色背景 1、可以使用 SolidColorBrush 来设置窗口的背景为单一颜色。 <Window x:Class"YourNamespace.MainWindow"xmlns&quo…...
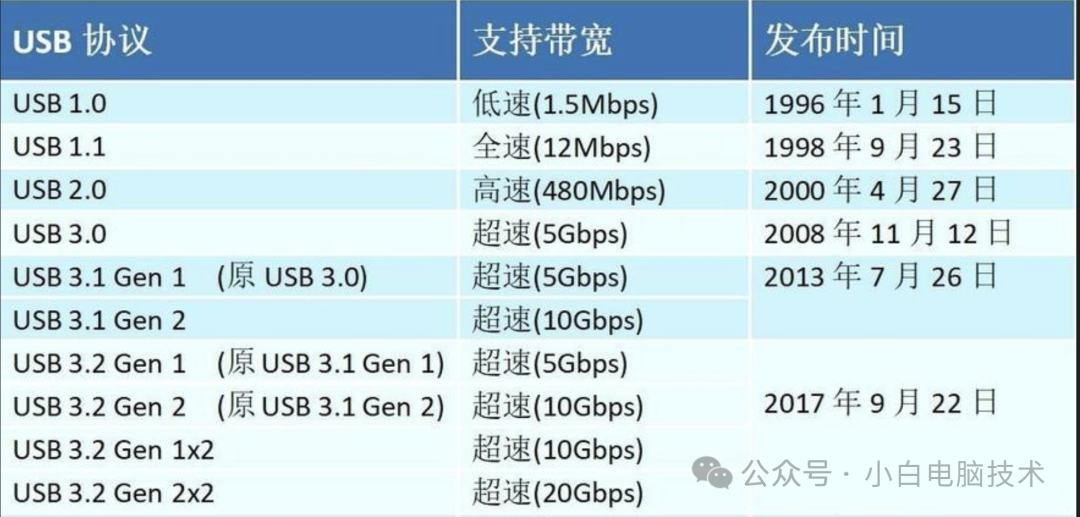
USB 3.0?USB 3.1?USB 3.2?怎么区分?
还记得小白刚接触电脑的时候,电脑普及的USB接口大部分是USB 2.0,还有少部分USB 1.0的(现在基本上找不到了)。 当时的电脑显示器,可能00后的小伙伴都没见过,它们大概长这样: 当时小白以为电脑最…...

Gitlab实战教程:打造企业级代码托管与协作平台!
目录 一、Gitlab概述1、Gitlab简介(1)Gitlab的定义(2)Gitlab与Git的关系(3)Gitlab的主要功能 2、Gitlab与Git的关系(1)Git的基本概念(2)Gitlab与Git的关联&am…...

更新C语言题目
1.以下程序输出结果是() int main() {int a 1, b 2, c 2, t;while (a < b < c) {t a;a b;b t;c--;}printf("%d %d %d", a, b, c); } 解析:a1 b2 c2 a<b 成立 ,等于一个真值1 1<2 执行循环体 t被赋值为1 a被赋值2 b赋值1 c-- c变成1 a<b 不成立…...

struct和C++的类
1.铺垫 1.1想看明白这章节,必须要懂得C语言的struct结构体、C语言深度解剖的static用法、理解声明与定义,C的类和static用法;否则看起来有些吃力 2.引子 2.1struct结构体里面只能存储内置类型;比如:char、short、 i…...

【数据结构与算法】LeetCode:图论
文章目录 LeetCode:图论岛屿数量(Hot 100)岛屿的最大面积腐烂的橘子(Hot 100)课程表(Hot 100) LeetCode:图论 岛屿数量(Hot 100) 岛屿数量 DFS: class So…...

YOLOv8 基于NCNN的安卓部署
YOLOv8 NCNN安卓部署 前两节我们依次介绍了基于YOLOv8的剪枝和蒸馏 本节将上一节得到的蒸馏模型导出NCNN,并部署到安卓。 NCNN 导出 YOLOv8项目中提供了NCNN导出的接口,但是这个模型放到ncnn-android-yolov8项目中你会发现更换模型后app会闪退。原因…...

【Python|接口自动化测试】使用requests发送http请求时添加headers
文章目录 1.前言2.HTTP请求头的作用3.在不添加headers时4.反爬虫是什么?5.在请求时添加headers 1.前言 本篇文章主要讲解如何使用requests请求时添加headers,为什么要加headers呢?是因为有些接口不添加headers时,请求会失败。 2…...

需求管理工具Jama Connect:与Jira/Slack/GitHub无缝集成,一站式解决复杂产品开发中的协作难题
在产品和软件开发的动态世界中,有效协作是成功的关键。然而,团队往往面临着阻碍进步和创新的重大挑战。了解这些挑战并找到强有力的解决方案,对于实现无缝、高效的团队协作至关重要。Jama Connect就是这样一种解决方案,它是一个功…...

CSP-J/S 复赛算法 背包DP
文章目录 前言背包DP的简介问题描述目标解决方法1. **定义状态**2. **状态转移方程**3. **初始化**4. **目标**举个例子动态规划解决背包问题的核心 DP背包问题示例代码问题描述代码实现核心代码讲解:举例:总结: 总结 前言 背包问题是算法竞…...

如何评估和部署 IT 运维系统?
如何才能将如此新兴、流行的技术转化为企业中实用的系统环境呢? 为此,我们采访了一家已经成功部署IT运维体系的大型企业的IT总监龙先生,请他给我们讲一下企业应该如何真正评估和部署自己的IT运维体系。 真理就是价值。 1.评估选择…...

正态分布的极大似然估计一个示例,详细展开的方程求解步骤
此示例是 什么是极大似然估计 中的一个例子,本文的目的是给出更加详细的方程求解步骤,便于数学基础不好的同学理解。 目标 假设我们有一组样本数据 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn,它们来自一个正态分布 N…...

s7-200SMART编程软件下载
1、官网: STEP 7 Micro/WIN SMART V2.2 完整版http://w2.siemens.com.cn/download/smart/STEP%207%20MicroWIN%20SMART%20V2.2.zip STEP 7 Micro/WIN SMART V2.3 完整版http://w2.siemens.com.cn/download/smart/STEP%207%20MicroWIN%20SMART%20V2.3.iso STEP 7 Mi…...

Linux驱动开发常用调试方法汇总
引言:在 Linux 驱动开发中,调试是一个至关重要的环节。开发者需要了解多种调试方法,以便能够快速定位和解决问题。 1.利用printk 描述: printk 是 Linux 内核中的一个调试输出函数,类似于用户空间中的 printf。它用于…...

将列表中的各字符串sn连接成为一个字符串s使用;将各sn间隔开os.pathsep.join()
【小白从小学Python、C、Java】 【考研初试复试毕业设计】 【Python基础AI数据分析】 将列表中的各字符串sn 连接成为一个字符串s 使用;将各sn间隔开 os.pathsep.join() [太阳]选择题 下列说法中正确的是? import os paths ["/a", "/b/c", "/d&q…...
算法题总结(八)——字符串
531、反转字符串二 给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。 如果剩余字符少于 k 个,则将剩余字符全部反转。如果剩余字符小于 2k 但大于或等于 k 个,…...

大数据开发--1.2 Linux介绍及虚拟机网络配置
目录 一. 计算机入门知识介绍 软件和硬件的概述 硬件 软件 操作系统概述 简单介绍 常见的系统操作 学习Linux系统 二. Linux系统介绍 简单介绍 发行版介绍 常用的发行版 三. Linux系统的安装和体验 Linux系统的安装 介绍 虚拟机原理 常见的虚拟机软件 体验Li…...

2024CSP-J复赛易错点
低级错误 不开long long见祖宗写代码要有输入,别没写输入就交写完代码要在本地测试,多想写极端测试数据,或对拍注意考官说文件夹怎么建,别文件夹建错,爆0别忘写freopen或忘给freopen去注释记着把.exe文件删掉考试时不…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
