第 17 场小白入门赛蓝桥杯
第 17 场小白入门赛
2 北伐军费
发现每次选大的更优,所以可以排序之后,先手取右边,后手取左边。
实际发现,对于 A − B A-B A−B 的结果来说,后手对于这个式子的贡献是 − − a i --a_i −−ai ,也就是 a i a_i ai ,实际答案就是数组之和。
void solve(){cin >> n;for(int i = 1; i <= n; i ++) cin >> a[i]; cout << accumulate(a + 1, a + n + 1, 0LL) << '\n';
}
4 三顾茅庐
找规律,对于 x ≤ y x\leq y x≤y 的情况 2 2 2 次一循环。
对于 x > y x>y x>y 的情况, x x x 每次回减 y y y 直到用完 k k k 次机会或者 x < = y x<=y x<=y 了,实际就是取模的过程。
void solve(){int x, y, k;cin >> x >> y >> k;if(!y){cout << x << '\n';return ;}if(x <= y){cout << ((k & 1) ? y - x : x) << '\n';}else{int t = (x / y);if(k > t){k -= t;x %= y;cout << ((k & 1) ? y - x : x) << '\n';}else{cout << x - k * y << '\n';}}
}
3 挑选武将
思路比较简单,将每个城池出现几个武将排序,从前往后枚举,只要当前选过的加上剩余的 ≥ k \geq k ≥k 即可。
蓝桥的 oj 比较垃圾,会 RE 只会返回 WA,非常不智能。
void solve(){cin >> n >> k;for(int i = 1; i <= n; i ++){cin >> x;a[x] ++;}vector<int> vc;for(int i = 1; i <= 100000; i ++){if(a[i]) vc.push_back(a[i]);} sort(vc.begin(), vc.end());vector<int> sum(vc.size());sum[0] = vc[0];for(int i = 1; i < vc.size(); i ++) sum[i] = vc[i] + sum[i - 1];auto ask = [&] (int l, int r){if(l > r) return 0LL;if(!l) return sum[r];return sum[r] - sum[l - 1];};int res = 0;for(int i = 0; i < vc.size() && (i + 1) <= k; i ++){if((i + 1) + ask(i + 1, vc.size() - 1) >= k) res = i + 1;}cout << res << '\n';
}
5 逆天改命
给你一个长度为 n n n 的数组 b b b ,你有一个 ∀ a i = 0 \forall a_i=0 ∀ai=0 的数组 a a a 。
可以执行以下两种操作 :
1,选取 [l, r] 区间,这个区间必须存在 a i = 0 a_i=0 ai=0 ,令所有数 + 1
2,选取 [l, r] 区间,这个区间不存在 a i = 0 a_i=0 ai=0 , 令所有数 - 1
很有意思的一道题目。
发现对于数组操作的过程中,一定不可能让最小值 ≥ 2 \geq 2 ≥2 。
因为最后一个 0 0 0 ,只能被选一次。
只要有 01 01 01 ,就能构造。
void solve(){int n, x, fg = 0;cin >> n;while(n --){cin >> x;fg |= (x == 0 || x == 1);}cout << (fg ? "YES" : "NO") << '\n';
}
6 智算士气
m = p 1 c 1 × p 2 c 2 × ⋯ × p i c i m=p_1^{c_1}\times p_2^{c_2}\times \cdots \times p_i ^{c_i} m=p1c1×p2c2×⋯×pici 。
对于每一位,至少存在一个数为 p i c i p_i^{c_i} pici ,正难则反,第 i i i 位共有 ( c i + 1 ) n − c i n (c_i+1)^n-c_i^n (ci+1)n−cin 种方案,考虑所有位,答案为 ∏ i ( c i + 1 ) n − c i n \prod _i (c_i+1)^n-c_i^n ∏i(ci+1)n−cin 。
map<int, int> pm;void solve(){ cin >> n >> m;for(int i = 2; i <= m / i; i ++){while(m % i == 0){pm[i] ++;m /= i;}} if(m > 1) pm[m] ++;int res = 1;for(auto [x, y] : pm){ res *= ksm(y + 1, n, mod) - ksm(y, n, mod);res %= mod;if(res < 0) res += mod;}cout << res;
}
相关文章:

第 17 场小白入门赛蓝桥杯
第 17 场小白入门赛 2 北伐军费 发现每次选大的更优,所以可以排序之后,先手取右边,后手取左边。 实际发现,对于 A − B A-B A−B 的结果来说,后手对于这个式子的贡献是 − − a i --a_i −−ai ,也就…...

@antv/x6 导出图片下载,或者导出图片为base64由后端去处理。
1、导出为文件的格式,比如 PNG graph.exportPNG(function (dataURL) {console.log(dataURL);let img document.getElementById(img) as HTMLImageElement;img.src dataURL;},{backgroundColor: #fff,padding: [20, 20, 20, 20],quality: 1,width: graph.options.w…...

从零到精通:AI大模型的全方位学习路径解析,非常详细收藏我这一篇就够了
一、初聊大模型 1、什么是大模型? 大模型,通常指的是在人工智能领域中的大型预训练模型。你可以把它们想象成非常聪明的大脑,这些大脑通过阅读大量的文本、图片、声音等信息,学习到了世界的知识。这些大脑(模型&…...

PowerShell脚本在自动化Windows开发工作流程中的应用
PowerShell脚本在自动化Windows开发工作流程中的应用 在当今快速迭代的软件开发环境中,自动化已成为提高开发效率、减少人为错误、保障项目稳定性的重要手段。特别是在Windows平台上,PowerShell以其强大的脚本编写能力和对系统管理的深度集成࿰…...

【力扣 | SQL题 | 每日四题】力扣1783,1757,1747,1623,1468,1661
昨天晚上睡着了,今天把昨天的每日一题给补上。 1. 力扣1783:大满贯数量 1.1 题目: 表:Players ------------------------- | Column Name | Type | ------------------------- | player_id | int | | player_na…...

《深入探究 C++中的函数模板特化:开启编程新境界》
在 C的广袤世界中,函数模板特化是一项强大而富有魅力的技术,它为程序员提供了更高的灵活性和效率。本文将带你深入了解 C中函数模板特化是如何实现的,揭开这一神秘面纱,让你在编程之路上更上一层楼。 一、函数模板的基础概念 在…...

RTEMS面试题汇总及参考答案
目录 RTEMS是什么?它在嵌入式系统中扮演什么角色? RTEMS的全称是什么? RTEMS的主要特点有哪些? RTEMS支持哪些处理器架构? RTEMS的可剥夺型内核和不可剥夺型内核有何不同? RTEMS 的微内核设计及其优势 RTEMS 如何实现多任务处理和调度 RTEMS 的任务调度策略有哪…...
)
螺蛳壳里做道场:老破机搭建的私人数据中心---Centos下Docker学习03(网络及IP规划)
3 网络及IP规划 3.1 容器连接网络初步规划 规划所有容器与虚拟机的三张网卡以macvlan的方式进行连接(以后根据应用可以更改),在docker下创建nat、wifi、nei、wai四张网卡,他们和虚拟机及宿主机上NIC的相关连接参数如下表所示&am…...

BLOOM 模型的核心原理、局限与未来发展方向解析
1. 引言 1.1 BLOOM 模型概述 BLOOM(BigScience Large Open-science Open-access Multilingual Language Model)是一款由多个国际研究团队联合开发的大型语言模型。BLOOM 模型旨在通过先进的 Transformer 架构处理复杂的自然语言生成与理解任务。它支持…...

Kubernetes 深度洞察:重新认识 Docker 容器的奇妙世界
《Kubernetes 深度洞察:重新认识 Docker 容器的奇妙世界》 在 Kubernetes 的学习进程中,对 Docker 容器的深入理解至关重要。这一节,我们将重新认识 Docker 容器,探索其在 Kubernetes 生态系统中的关键作用。 一、Docker 容器的基本概念 Docker 容器是一种轻量级的虚拟化…...

柔性作业车间调度(FJSP)
1.1 调度问题的研究背景 生产调度是指针对一项可分解的工作(如产品制造),在尽可能满足工艺路线、资源情况、交货期等约束条件的前提下,通过下达生产指令,安排其组成部分(操作)所使用的资源、加工时间及加工的先后顺序,以获得产品制造时间或成本最优化的一项工作。 一般研究车间…...

速盾:游戏用CDN可以吗?
游戏用CDN是一种常见的解决方案,可以提高游戏的网络性能和加载速度。CDN(Content Delivery Network,内容分发网络)能够将游戏的静态资源分布到全球各地的边缘节点上,使用户可以从离他们最近的节点获取游戏资源…...

《重生到现代之从零开始的C语言生活》—— 字符函数和字符串函数
字符函数和字符串函数 字符分类函数 大家知道字符是分为很多种类型的 就比如说’a’ ‘1’ A’等等,所以我们需要一种函数来完成字符函数的分类 这就是字符分类函数 函数需要包含头文件<ctype.h> 函数的运行规则是:如果符合下列参数就返回真 …...

双指针:滑动窗口
题目描述 给定两个字符串 S 和 T,求 S 中包含 T 所有字符的最短连续子字符串的长度,同时要求时间复杂度不得超过 O(n)。 输入输出样例 输入是两个字符串 S 和 T,输出是一个 S 字符串的子串。样例如下: 在这个样例中,…...

云原生(四十八) | Nginx软件安装部署
文章目录 Nginx软件安装部署 一、Nginx软件部署步骤 二、安装与配置Nginx Nginx软件安装部署 一、Nginx软件部署步骤 第一步:安装 Nginx 软件 第二步:把 Nginx 服务添加到开机启动项 第三步:配置 Nginx 第四步:启动Nginx …...

【WPF开发】如何设置窗口背景颜色以及背景图片
在WPF中,可以通过设置窗口的 Background 属性来改变窗口的背景。以下是一些设置窗口背景的不同方法: 一、设置纯色背景 1、可以使用 SolidColorBrush 来设置窗口的背景为单一颜色。 <Window x:Class"YourNamespace.MainWindow"xmlns&quo…...
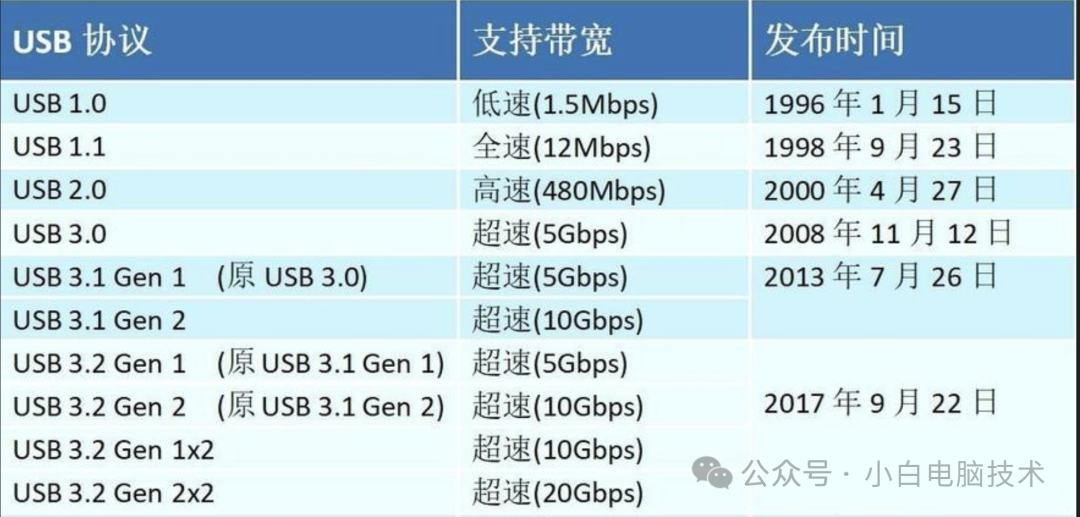
USB 3.0?USB 3.1?USB 3.2?怎么区分?
还记得小白刚接触电脑的时候,电脑普及的USB接口大部分是USB 2.0,还有少部分USB 1.0的(现在基本上找不到了)。 当时的电脑显示器,可能00后的小伙伴都没见过,它们大概长这样: 当时小白以为电脑最…...

Gitlab实战教程:打造企业级代码托管与协作平台!
目录 一、Gitlab概述1、Gitlab简介(1)Gitlab的定义(2)Gitlab与Git的关系(3)Gitlab的主要功能 2、Gitlab与Git的关系(1)Git的基本概念(2)Gitlab与Git的关联&am…...

更新C语言题目
1.以下程序输出结果是() int main() {int a 1, b 2, c 2, t;while (a < b < c) {t a;a b;b t;c--;}printf("%d %d %d", a, b, c); } 解析:a1 b2 c2 a<b 成立 ,等于一个真值1 1<2 执行循环体 t被赋值为1 a被赋值2 b赋值1 c-- c变成1 a<b 不成立…...

struct和C++的类
1.铺垫 1.1想看明白这章节,必须要懂得C语言的struct结构体、C语言深度解剖的static用法、理解声明与定义,C的类和static用法;否则看起来有些吃力 2.引子 2.1struct结构体里面只能存储内置类型;比如:char、short、 i…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
