柔性作业车间调度(FJSP)
1.1 调度问题的研究背景
生产调度是指针对一项可分解的工作(如产品制造),在尽可能满足工艺路线、资源情况、交货期等约束条件的前提下,通过下达生产指令,安排其组成部分(操作)所使用的资源、加工时间及加工的先后顺序,以获得产品制造时间或成本最优化的一项工作。
一般研究车间调度问题时,都会以经典的作业车间调度问题(job shop scheduling problem,JSP)为基础进行研究,每个工件的每道工序只能在一台机器上加工,并且仅仅只能加工一次,加工时间是确定的,如图1.1所示。

随着柔性制造系统和数控加工中心等带有一定柔性的生产系统逐渐出现,以往经典作业车间调度的研究成果不能非常快速地直接应用于新的制造模式中,于是柔性作业车间调度问题(flexible jobshop scheduling problem,FJSP)也就成为研究重点,它是JSP的一种扩展,工件的每道工序可以在多台机器上进行加工,加工时间不一定相同。工件的每一道工序可以在多台相同或不同的机器上进行加工。实际生产中可以按照资源负荷情况,灵活地进行资源的选择,提高加工的灵活性。
1.2 调度问题描述和分类
1.2.1 调度问题的描述
调度问题的一般性定义为:在一定的约束条件下,把有限的资源在时间上分配给若干个任务,以满足或优化一个或多个性能指标。
在制造业中,车间调度问题可以描述为:n个工件在m台机器上加工;一个工件有多道工序,每道工序可以在若干台机器上加工,并且必须按一些可行的工艺次序进行加工;每台机器可以加工工件的若干工序,并且在不同的机器上加工的工序集可以不同。调度的目标是将工件合理地安排到各机器,并合理地安排工件的加工次序和加工开始时间,使约束条件被满足,同时优化一些性能指标。在实际制造系统中,还要考虑刀具、托盘和物料搬运系统的调度问题。
1.2.2 车间调度问题的分类
1.流水车间调度问题
在流水车间调度问题(flow shop scheduling problem,FSP)中,加工系统有一组功能不同的机床,待加工的工件包含多道工序,每道工序在一台机床上加工,所有工件的加工路线都是相同的。每个工件工序之间有先后顺序约束。
2.作业车间调度问题
在作业车间调度问题(job shop scheduling problem,JSP)中,加工系统有一组功能不同的机床,待加工的工件包含多道工序,每道工序在一台机床上加工,工件的加工路线互不相同,每个工件工序之间有先后顺序约束。
2.1 柔性作业车间调度问题的描述
2.1.1 柔性作业车间调度问题的描述与分类
柔性作业车间调度问题(flexible job shop scheduling problem,FJSP)的描述如下:n个工件(J1,J2,…,Jm)要在m台机器(M1,M2,…,Mm)上加工;每个工件包含一道或多道工序;工序顺序是预先确定的;每道工序可以在多台不同加工机器上进行加工;工序的加工时间随加工机器的不同而不同;调度目标是为每道工序选择最合适的机器,确定每台机器上各道工序的最佳加工顺序及开工时间,使整个系统的某些性能指标达到最优。因此,柔性作业车间调度问题包含两个子问题:确定各工件的加工机器(机器选择子问题)和确定各个机器上的加工先后顺序(工序排序子问题)。
此外,在加工过程中还需要满足下面的约束条件。
- 同一台机器在某一时刻只能加工一个工件。
- 同一工件的同一道工序在同一时刻只能被一台机器加工。
- 每个工件的每道工序一旦开始,加工便不能中断。
- 不同工件之间具有相同的优先级。
- 不同工件的工序之间没有先后约束,同一工件的工序之间有先后约束。
- 所有工件在零时刻都可以被加工。
柔性作业车间调度问题根据资源选择限制条件和柔性程度,可以分为完全柔性作业车间调度问题(total FJSP,T-FJSP)和部分柔性作业车间调度问题(partialFJSP,P-FJSP),分别如表2.1、表2.2所示。在T-FJSP中,所有工件的每一道工序都可以在可选择的机器中选择任何一台进行加工;而在P-FJSP中,至少存在一道工序的加工机器只能是可选择的机器中的部分机器,即机器集的真子集来进行加工。也可以说,T-FJSP只是P-FJSP的一个特例。P-FJSP更加符合实际生产系统中的调度问题,研究P-FJSP比T-FJSP更具有实际意义,P-FJSP要比T-FJSP更加复杂。

表2.2是一个包括2个工件、5台机器的P-FJSP的加工机器和加工时间表。其中,“一”表示此工序不能选择上面对应的机器进行加工。如果所有的“一”都有对应的加工时间,表明所有的机器都可以进行选择加工,就是T-FJSP,如表2.1所示。
2.1.2 FJSP的析取图模型
在FJSP中,存在循环排列的特性,即同一个工件的多道工序可以在同一台机器上连续或间隔加工。当FJSP中每道工序确定了加工机器之后,即转变为一般的作业车间调度问题。而析取图(disjunctive graph)模型是描述车间调度问题的一种重要形式。析取图模型G=(N,A,E)是由Balas提出的,其定义为:N是所有工序组成的节点集,其中0和*表示两个虚设的起始工序和终止工序,每个节点的权值等于此节点工序在对应机器上的加工时间;A是连接同一个工件的邻接工序间的有向弧集(实线),表示工序之间的先后加工顺序约束;E是连接在同一台机器上相邻加工工序间的析取弧集(虚线)。E上每个析取弧是双向的,可视为包含两个方向相反的弧,并且由每台机器i上的析取弧子集构成。以表2.3所示调度问题为例,其中包含三个工件、三台机器和九道工序。如图2.1(a)所示,节点集N={0,O11,O12,O13,O21,O22,O23,O31,O32,O33,*}。有向弧集A={(O11,O12),(O12,O13),(O21,O22),(O22,O23),(O31,O32),(O32,O33)}。
 对由第i台机器(i∈Ω)所加工的工序而言,每一个加工方案等价于E中的一个选择,即在E2的每个双向弧中选择一个确定的方向,记为一个选择S。一个环就是从一个工序出发到此工序终止的路径。如果一个选择S,不包含任何有向环(directed cycle),则称为非循环(acyclic),对应着第i台机器上所有工序的一个调度。在i∈Ω中,对每个E,求得一个选择S1,所有机器选择的并集S称为完全选择;否则S为部分选择。无论S是一个部分选择还是一个完全选择,都有唯一的有向图Ds=(N,AUS)与之相对应。当有向图是非循环图时,表示一个可行调度,并且所有选择S,也必是非循环的;反之,由非循环选择S1组成的有向图不一定是非循环的。如图2.1(a)所示为表2.3中调度问题的一个可行调度的有向图,图2.1(b)所示为对应图2.1(a)的甘特图,其中机器1上的选择S1={O21,O11,O32},机器2上的选择S2={O31,O12,O23},机器3上的选择S3={O22,O13,O33}。
对由第i台机器(i∈Ω)所加工的工序而言,每一个加工方案等价于E中的一个选择,即在E2的每个双向弧中选择一个确定的方向,记为一个选择S。一个环就是从一个工序出发到此工序终止的路径。如果一个选择S,不包含任何有向环(directed cycle),则称为非循环(acyclic),对应着第i台机器上所有工序的一个调度。在i∈Ω中,对每个E,求得一个选择S1,所有机器选择的并集S称为完全选择;否则S为部分选择。无论S是一个部分选择还是一个完全选择,都有唯一的有向图Ds=(N,AUS)与之相对应。当有向图是非循环图时,表示一个可行调度,并且所有选择S,也必是非循环的;反之,由非循环选择S1组成的有向图不一定是非循环的。如图2.1(a)所示为表2.3中调度问题的一个可行调度的有向图,图2.1(b)所示为对应图2.1(a)的甘特图,其中机器1上的选择S1={O21,O11,O32},机器2上的选择S2={O31,O12,O23},机器3上的选择S3={O22,O13,O33}。

在非循环有向图Ds中,从起点0到终点*的最长路径称为关键路径(critical path),其长度等于该调度的最大完工时间。用析取图描述调度问题,就是为了找到此关键路径,并使之最小。属于关键路径上的每道工序称为关键工序。在同一台机器上紧邻的几个关键工序的组合称为关键块,同一个机器上可能有多个关键块,其中每个关键块的第一个工序为块首工序,每个关键块的最后工序称为块尾工序,其他称为内部工序。如图2.1(b)中画虚线的O21、O11、O12、O13、O33表示关键工序;有两个关键块,即{O21,O11}、{O13,O33};关键路径的长度等于16。
2.1.3 FJSP 评价指标
在FJSP的求解过程中,调度方案优劣的评价需要通过一定的目标函数来判断,目标函数也就是常用的评价指标。FJSP中不仅包括了经典JSP常用的评价指标,而且还有其他的评价指标。下面列出文献中较为常用的几个评价指标。
(1)最大完工时间最小 完工时间是每个工件最后一道工序完成的时间,其中最大的那个时间就是最大完工时间(makespan)。它是衡量调度方案的最根本指标,主要体现车间的生产效率,也是FJSP研究中应用最广泛的评价指标之一,可表示为(2.10)所示。

(2)机器最大负荷最小 在FJSP求解中,存在选择机器的过程,各台机器的负荷随着不同的调度方案而不同。负荷最大的机器就是瓶颈设备。要提高每台机器的利用率,必须使得各台机器的负荷尽量小且平衡,可表示为
(3)总机器负荷最小 工序在不同机器上的加工时间是不同的,那么总的机器负荷随着不同的调度方案而不同。尽量使最大完工时间一样的情况下,减少所有机器的总消耗,可表示为
2.3 柔性作业车间调度问题的研究方法

相关文章:

柔性作业车间调度(FJSP)
1.1 调度问题的研究背景 生产调度是指针对一项可分解的工作(如产品制造),在尽可能满足工艺路线、资源情况、交货期等约束条件的前提下,通过下达生产指令,安排其组成部分(操作)所使用的资源、加工时间及加工的先后顺序,以获得产品制造时间或成本最优化的一项工作。 一般研究车间…...

速盾:游戏用CDN可以吗?
游戏用CDN是一种常见的解决方案,可以提高游戏的网络性能和加载速度。CDN(Content Delivery Network,内容分发网络)能够将游戏的静态资源分布到全球各地的边缘节点上,使用户可以从离他们最近的节点获取游戏资源…...

《重生到现代之从零开始的C语言生活》—— 字符函数和字符串函数
字符函数和字符串函数 字符分类函数 大家知道字符是分为很多种类型的 就比如说’a’ ‘1’ A’等等,所以我们需要一种函数来完成字符函数的分类 这就是字符分类函数 函数需要包含头文件<ctype.h> 函数的运行规则是:如果符合下列参数就返回真 …...

双指针:滑动窗口
题目描述 给定两个字符串 S 和 T,求 S 中包含 T 所有字符的最短连续子字符串的长度,同时要求时间复杂度不得超过 O(n)。 输入输出样例 输入是两个字符串 S 和 T,输出是一个 S 字符串的子串。样例如下: 在这个样例中,…...

云原生(四十八) | Nginx软件安装部署
文章目录 Nginx软件安装部署 一、Nginx软件部署步骤 二、安装与配置Nginx Nginx软件安装部署 一、Nginx软件部署步骤 第一步:安装 Nginx 软件 第二步:把 Nginx 服务添加到开机启动项 第三步:配置 Nginx 第四步:启动Nginx …...

【WPF开发】如何设置窗口背景颜色以及背景图片
在WPF中,可以通过设置窗口的 Background 属性来改变窗口的背景。以下是一些设置窗口背景的不同方法: 一、设置纯色背景 1、可以使用 SolidColorBrush 来设置窗口的背景为单一颜色。 <Window x:Class"YourNamespace.MainWindow"xmlns&quo…...
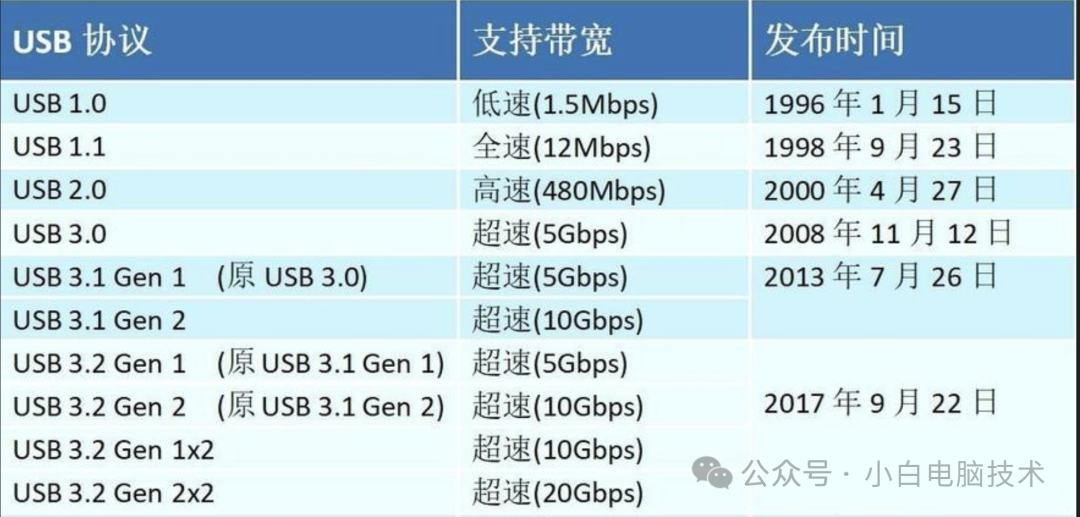
USB 3.0?USB 3.1?USB 3.2?怎么区分?
还记得小白刚接触电脑的时候,电脑普及的USB接口大部分是USB 2.0,还有少部分USB 1.0的(现在基本上找不到了)。 当时的电脑显示器,可能00后的小伙伴都没见过,它们大概长这样: 当时小白以为电脑最…...

Gitlab实战教程:打造企业级代码托管与协作平台!
目录 一、Gitlab概述1、Gitlab简介(1)Gitlab的定义(2)Gitlab与Git的关系(3)Gitlab的主要功能 2、Gitlab与Git的关系(1)Git的基本概念(2)Gitlab与Git的关联&am…...

更新C语言题目
1.以下程序输出结果是() int main() {int a 1, b 2, c 2, t;while (a < b < c) {t a;a b;b t;c--;}printf("%d %d %d", a, b, c); } 解析:a1 b2 c2 a<b 成立 ,等于一个真值1 1<2 执行循环体 t被赋值为1 a被赋值2 b赋值1 c-- c变成1 a<b 不成立…...

struct和C++的类
1.铺垫 1.1想看明白这章节,必须要懂得C语言的struct结构体、C语言深度解剖的static用法、理解声明与定义,C的类和static用法;否则看起来有些吃力 2.引子 2.1struct结构体里面只能存储内置类型;比如:char、short、 i…...

【数据结构与算法】LeetCode:图论
文章目录 LeetCode:图论岛屿数量(Hot 100)岛屿的最大面积腐烂的橘子(Hot 100)课程表(Hot 100) LeetCode:图论 岛屿数量(Hot 100) 岛屿数量 DFS: class So…...

YOLOv8 基于NCNN的安卓部署
YOLOv8 NCNN安卓部署 前两节我们依次介绍了基于YOLOv8的剪枝和蒸馏 本节将上一节得到的蒸馏模型导出NCNN,并部署到安卓。 NCNN 导出 YOLOv8项目中提供了NCNN导出的接口,但是这个模型放到ncnn-android-yolov8项目中你会发现更换模型后app会闪退。原因…...

【Python|接口自动化测试】使用requests发送http请求时添加headers
文章目录 1.前言2.HTTP请求头的作用3.在不添加headers时4.反爬虫是什么?5.在请求时添加headers 1.前言 本篇文章主要讲解如何使用requests请求时添加headers,为什么要加headers呢?是因为有些接口不添加headers时,请求会失败。 2…...

需求管理工具Jama Connect:与Jira/Slack/GitHub无缝集成,一站式解决复杂产品开发中的协作难题
在产品和软件开发的动态世界中,有效协作是成功的关键。然而,团队往往面临着阻碍进步和创新的重大挑战。了解这些挑战并找到强有力的解决方案,对于实现无缝、高效的团队协作至关重要。Jama Connect就是这样一种解决方案,它是一个功…...

CSP-J/S 复赛算法 背包DP
文章目录 前言背包DP的简介问题描述目标解决方法1. **定义状态**2. **状态转移方程**3. **初始化**4. **目标**举个例子动态规划解决背包问题的核心 DP背包问题示例代码问题描述代码实现核心代码讲解:举例:总结: 总结 前言 背包问题是算法竞…...

如何评估和部署 IT 运维系统?
如何才能将如此新兴、流行的技术转化为企业中实用的系统环境呢? 为此,我们采访了一家已经成功部署IT运维体系的大型企业的IT总监龙先生,请他给我们讲一下企业应该如何真正评估和部署自己的IT运维体系。 真理就是价值。 1.评估选择…...

正态分布的极大似然估计一个示例,详细展开的方程求解步骤
此示例是 什么是极大似然估计 中的一个例子,本文的目的是给出更加详细的方程求解步骤,便于数学基础不好的同学理解。 目标 假设我们有一组样本数据 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn,它们来自一个正态分布 N…...

s7-200SMART编程软件下载
1、官网: STEP 7 Micro/WIN SMART V2.2 完整版http://w2.siemens.com.cn/download/smart/STEP%207%20MicroWIN%20SMART%20V2.2.zip STEP 7 Micro/WIN SMART V2.3 完整版http://w2.siemens.com.cn/download/smart/STEP%207%20MicroWIN%20SMART%20V2.3.iso STEP 7 Mi…...

Linux驱动开发常用调试方法汇总
引言:在 Linux 驱动开发中,调试是一个至关重要的环节。开发者需要了解多种调试方法,以便能够快速定位和解决问题。 1.利用printk 描述: printk 是 Linux 内核中的一个调试输出函数,类似于用户空间中的 printf。它用于…...

将列表中的各字符串sn连接成为一个字符串s使用;将各sn间隔开os.pathsep.join()
【小白从小学Python、C、Java】 【考研初试复试毕业设计】 【Python基础AI数据分析】 将列表中的各字符串sn 连接成为一个字符串s 使用;将各sn间隔开 os.pathsep.join() [太阳]选择题 下列说法中正确的是? import os paths ["/a", "/b/c", "/d&q…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

