题目:最左边的数字
问题 - 1060 (hdu.edu.cn)
解题思路:
数字很大,使用科学计数法。则,我们需要的是a的整数位,最终求出a即可。
取对数:nlgn=m+lga,移项:lga=nlgn-m,接下来我们需要求m。
设0<x<1,令a=10^x,则n^n=(10^x)*(10^m)=10^(x+m),再取对数:nlgn=x+m,移项:m=(nlgn)-m,因为m为整数,所以 m为nlgn的向下取整。所以。
AC代码:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;int main()
{int t;cin >> t;while(t--){int n;cin >> n;double x = n * log10(n);x -= (ll)x; // ll可以x向下取整cout << (int)pow(10.0,x) << '\n'; // int使我们思路里需要的a保留整数位,即题目左边的数。// pow里10.0为避免错误,参数都是同类型则返回值相同类型 } return 0;} 知识点:
科学计数法
相关文章:
题目:最左边的数字
问题 - 1060 (hdu.edu.cn) 解题思路: 数字很大,使用科学计数法。则,我们需要的是a的整数位,最终求出a即可。 取对数:nlgnmlga,移项:lganlgn-m,接下来我们需要求m。 …...

第 4 章 Spring IoC容器之BeanFactory
Spring 的 IoC 容器是一个提供 IoC 支持的轻量级容器,除了基本的 IoC 支持,它作为轻量级容器还提供了 IoC 之外的支持。 Spring 提供了两种容器类型:BeanFactory 和 ApplicationContext: BeanFactory,基础类型 IoC 容…...

滚雪球学Oracle[2.3讲]:Oracle Listener配置与管理
全文目录: 前言一、Oracle Listener的基础概念1.1 什么是Oracle Listener?Listener的作用: 1.2 Oracle Listener的配置文件示例listener.ora配置文件: 1.3 启动与管理Listener 二、多Listener配置与负载分担2.1 多Listener的应用场…...

免费送源码:Javaspringboot++MySQL springboot 社区互助服务管理系统小程序 计算机毕业设计原创定制
摘 要 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受居民的喜爱,社区互助服务管理系统小程序被居民普遍使用,为…...

成都睿明智科技有限公司抖音电商新蓝海的领航者
在当今这个数字化浪潮汹涌的时代,电商行业正以惊人的速度迭代升级,而抖音电商作为新兴势力,更是凭借其庞大的用户基数、精准的算法推荐和高度互动的社区氛围,成为了众多商家竞相追逐的蓝海市场。在这片充满机遇与挑战的海洋中&…...

不可错过!CMU最新《生成式人工智能大模型》课程:从文本、图像到多模态大模型
1. 课程简介 从生成图像和文本到生成音乐和艺术,生成模型一直是人工智能的关键挑战之一。本课程将探讨推动生成模型和基础模型(Foundation Models)最近进展的机器学习和人工智能技术。学生将学习、开发并应用最先进的算法,使机器…...

重庆数字孪生工业互联网可视化技术,赋能新型工业化智能制造工厂
重庆作为西南地区的重要工业基地,正积极探索和实践数字孪生、工业互联网及可视化技术在智能制造领域的深度融合,致力于打造新型工业化智能制造工厂,为制造业的高质量发展注入强劲动力。 在重庆的智能制造工厂中,数字孪生技术被广…...

Qt QPushButton clicked信号浅析
前言 Qt 的 QPushButton clicked 信号原型: void clicked(bool checked false);通常,使用 Qt 的 QPushButton clicked 点击信号时,会以如下方式使用: connect(ui->pushButton, &QPushButton::clicked, this, [](){qDeb…...

Python时间戳转日期
在Python中,你可以使用datetime模块将时间戳转换为日期。时间戳通常是一个表示自1970年1月1日(UTC)以来的秒数的浮点数或整数。 以下是一个简单的示例,展示了如何将时间戳转换为日期和时间: import datetime# 示例时…...

对 LLM 工具使用进行统一
我们为 LLM 确立了一个跨模型的 统一工具调用 API。有了它,你就可以在不同的模型上使用相同的代码,在 [Mistral] 或 [Llama]) 等模型间自由切换,而无需或很少需要根据模型更改工具调用相关的代码。此外,我们还在 transformers 中新…...

webpack/vite的区别
Webpack和Vite都是前端开发中常用的构建工具,它们在多个方面存在显著的区别。以下是对这两个构建工具的详细比较: 一、基础概念与定位 Webpack Webpack是一个现代JavaScript应用程序的静态模块打包器(module bundler)。它允许开发…...
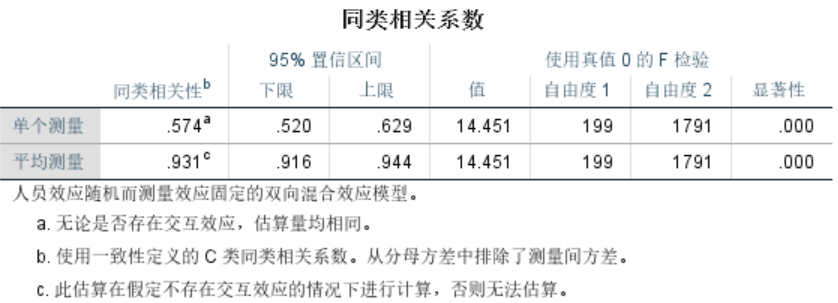
【笔记】信度检验
一、信度 信度是指测量结果的一致性和稳定性。 1.一致性(Consistency) 一致性指的是测量工具内部各个部分或项目之间的协调一致程度。高一致性意味着测量工具的不同部分都在测量同一个概念或特质。 例子:智力测试 假设我们有一个包含100…...

使用Python实现无人机路径规划的灰狼优化算法
目录 使用 Python 实现无人机路径规划的灰狼优化算法引言1. 灰狼优化算法概述1.1 定义1.2 算法原理1.3 灰狼的狩猎策略1.4 算法步骤 2. Python 中的灰狼优化算法实现2.1 安装必要的库2.2 定义类2.2.1 灰狼类2.2.2 群体类2.2.3 路径规划类 2.3 示例程序 3. 灰狼优化算法的优缺点…...

理解递归和回溯
文章目录 什么是递归回溯 什么是递归 回溯 //使用递归回溯来给小球找路//说明//1. map 表示地图//2. i,j 表示从地图的哪个位置开始出发 (1,1)//3. 如果小球能到 map[6][5] 位置,则说明通路找到.//4. 约定: 当map[i][j] 为 0 表示该点没有走过 当为 1 表…...
)
知识图谱入门——3:工具分类与对比(知识建模工具:Protégé、 知识抽取工具:DeepDive、知识存储工具:Neo4j)
在知识图谱构建的过程中,针对不同的任务和需求,我们可以使用多种工具。为了帮助你快速选择合适的工具,本文将常用工具按类别进行分类介绍,并对比其优缺点,方便你在不同场景中做出最佳选择。 文章目录 1. 知识建模工具…...

使用指标进行量化交易时,有哪些需要注意的风险点呢
炒股自动化:申请官方API接口,散户也可以 python炒股自动化(0),申请券商API接口 python炒股自动化(1),量化交易接口区别 Python炒股自动化(2):获取…...

数据结构阶段测试2的一点小补充
数据结构阶段测试2的一点小补充 1.已知⼩根堆为8,15,10,21,34,16,12,删除关键字8之后需重建堆,最后的叶⼦ 节点为() A. 34 B. 21 C. 16 D. 12 解题思路 向下调整算法删除堆顶元素 💡 答案:C 删除堆顶元素的思路: …...

量化交易里面的挂单成交率大概是多少呢
炒股自动化:申请官方API接口,散户也可以 python炒股自动化(0),申请券商API接口 python炒股自动化(1),量化交易接口区别 Python炒股自动化(2):获取…...

【Android 14源码分析】Activity启动流程-3
忽然有一天,我想要做一件事:去代码中去验证那些曾经被“灌输”的理论。 – 服装…...

Javascript客户端时间与服务器时间
在Java代码中使用new Date(),获取的是本机时间; 但是在Javascript 中使用new Date(),获取的却是访问该页面的客户端时间。 这样,就可能会出现一个问题:我的电脑时间比正常时间要快,我访问一个页面&#x…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...
