数据结构之排序(5)
摘要:本文主要讲各种排序算法,注意它们的时间复杂度
概念
将各元素按关键字递增或递减排序顺序重新排列
评价指标
稳定性: 关键字相同的元素经过排序后相对顺序是否会改变
时间复杂度、空间复杂度
分类
内部排序——数据都在内存中
外部排序——数据太多,无法全部放入内存
一、插入排序
算法思想:每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成
比27大的数往后挪

void InsertSort() {int i, j ,temp;for (i = 1;i <= n;i++)//将各元素插入已排好序的序列中{if (A[i] < A[i - 1]){//若A[i]关键字小于前驱temp = A[i];//用temp暂存A[i]for (j = i - 1;j >= 0 && A[j] > temp;--j)//检查所有前面已排好序的元素{A[j + 1] = A[j];//所有大于temp的元素都向后挪位}A[j + 1] = temp;//复制到插入位置}}
}void InsertSort() {int i, j;for (i = 2;i <= n;i++)//依次将A[2]~A[n]插入到前面已排序序列{if (A[i] < A[i - 1]) {//若A[i]关键码小于其前驱,将A[i]插入有序表A[0] = A[i];//复制为哨兵,A[0]不存放元素for (j = i - 1;A[0] < A[j];--j)//从后往前查找待插入位置{A[j + 1] = A[j];//向后挪位}}A[j + 1] = A[0];//复制到插入位置}}
}优点:不用每轮循环判断j>=0
空间复杂度:O(1)
时间复杂度:主要来自对比关键字、移动元素 若n个元素,则需要n-1趟处理
最好时间复杂度(全部有序):O(n)
最坏(逆序):O(n^2)
平均O(n^2)
算法稳定性:稳定
优化——折半插入排序
当low>high时折半查找停止,应将[low,i-1]内的元素全部右移,并将A[0]复制到low所指位置
当A[mid]==A[0]时,为了保证算法的“稳定性”,应继续在mid 所指位置右边寻找插入位置
void InsertSort() {int i,j,low, high, mid;for (i = 2;i <= n;i++) {//依次将A[2]~A[n]插入前面的已排序序列A[0] = A[i];//将A[i]暂存到A[0]low = 1;high = i - 1;//设置折半查找的范围while (low <= high) {//折半查找mid = (low + high) / 2;//取中间点if (A[mid] > A[0])high = mid - 1;//查找左半子表else low = mid + 1;//查找右半子表}for (j = i - 1;j >= high + 1;--j)A[j + 1] = A[j];//统一后移元素,空出插入位置A[high + 1] = A[0];//插入操作}
}二、希尔排序(Shell sort)
最好情况:原本就有序
比较好的情况:基本有序
希尔排序:先追求表中元素部分有序,再逐渐逼近全局有序
先将待排序表分割成若干形如L[i,i+d,i+2d,…,i+kd]的“特殊”子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止
重点:给出增量序列,分析每一趟排序后的状态
void ShellSort() {int d, i, j;//A[0]只是暂存单元,不是哨兵,当j<=0时,插入位置已到for (d = n / 2;d >= 1;d = d / 2)//步长变化for (i = d ;i <n;++i)if (A[i] < A[i - d]) {//需将A[i]插入有序增量子表A[0] = A[i];//暂存在A[0]for (j = i - d;j > 0 && A[0] < A[j];j -= d)A[j + d] = A[j];//记录后移,查找插入的位置A[j + d] = A[0];//插入}
}三、交换排序
1、冒泡排序
从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即A[i-1]>A[i]),则交换它们,直到序列比较完。称这样过程为“一趟”冒泡排序。
void BubbleSort() {for (int i = 0;i < n - 1;i++) {bool flag = false;//表示本趟冒泡是否发生交换的标志for (int j=n;j > i;j--)//一趟冒泡过程if (A[j - 1] > A[j]) {//若为逆序swap(A[j - 1], A[j]);//交换flag = true;}if (flag == false)return;//本趟遍历后没有发生交换,说明表已经有序}
}2、快速排序
算法思想:
在待排序表L[1,…n]中任取元素pivot作为枢轴(或基准,通常取首元素),
通过一趟排序将待排序表划分成独立的两部分L[1…k-1]和L[k+1…n], 使得L[1…k-1]中的所有元素小于pivot,L[k+1…n]大于等于,则pivot放在了其最终位置L(k)上,这个过程称为一次“划分”。
然后分别递归地对两个子表重复上述过程,直到每部分内只有一个元素或空为止,即所有元素放在了最终位置上
//用第一个元素将待排序序列划分为左右两个部分
int Partition( int low, int high) {int pivot = A[low];//第一个元素作为枢轴while (low < high) {//用low、high搜索枢轴的最终位置while (low < high && A[high] >= pivot) --high;A[low] = A[high];//比枢轴小的元素移动到左端while (low < high && A[low] <= pivot) ++low;A[high] = A[low];//大 右}A[low] = pivot;//枢轴元素存放到最终位置return low;//返回存放枢轴的最终位置
}//快速排序
void QuickSort(int low, int high) {if (low < high) {//递归跳出的条件int pivotpos = Partition( low, high);//划分QuickSort( low, pivotpos - 1);//划分左子表QuickSort(pivotpos + 1, high);//划分右子表}
}
算法表现主要取决于递归深度,若每次“划分”越均匀,则递归深度越低。“划分”越不均匀,递归深度越深
三、选择排序
每一趟在待排序元素中选取关键字最小(或最大)的元素加入有序子序列
1、简单选择排序
void SelectSort() {for (int i = 0;i < n - 1;i++) {//一共进行n-1趟int min = i;//记录最小元素位置for (int j = i + 1;j < n;j++)//在A[i…n-1]中选择最小元素if (A[j] < A[min]) min = j;//更新最小元素位置if (min != i) swap(A[i], A[min]);//封装的swap()函数共移动元素3次}
}2、堆排序
若满足L(i)>=L(2i)且L(i)>=L(2i+1)(1<=i<=n/2)——大根堆(大顶堆)
思路:
把所有非终端结点都检查一遍,是否满足大根堆的要求,如果不满足,则进行调整
顺序存储的完全二叉树中,非终端结点编号i<=[n/2]
检查当前结点是否满足根>=左、右
若不满足,将当前结点与更大的一个孩子互换
i的左孩子2i, 右孩子2i+1,父结点[i/2]
若元素互换破坏了下一级的堆,则采用相同的方法继续往下调整(小元素不断“下坠”)
(这个比较复杂,附视频:8.4_2_堆排序_哔哩哔哩_bilibili)
void BuildMaxHeap(int len) {for (int i = len / 2;i > 0;i--)//从后往前调整所有非终端结点,即非叶子结点HeadAdjust(i,len);
}//将以k为根的子树调整为大根堆
void HeadAdjust(int k,int len) {A[0] = A[k];//A[0]暂存子树的根节点for (int i = 2*k;i <= len;i*=2) {//从左子树开始,沿key较大的子结点向下筛选if (i < len && A[i] < A[i + 1])//i < len 保证有右兄弟i++;//取key较大的子结点的下标if (A[0] >= A[i]) break;//筛选结束else {A[k] = A[i];//将A[i]调整到双亲结点上k = i;//修改k值,以便继续向下筛选}}A[k] = A[0];//被筛选结点的值放入最终位置
}结论:一个结点,每“下坠”一层,最多只需对比关键字2次
若树高为h,某结点在第i层,则将这个结点向下调整最多只需要”下坠“h-i层,关键字对比次数不超过 2(h-i)
基于大根堆进行排序
//堆排序的完整逻辑
void HeapSort(int len) {BuildMaxHeap(len);//初始建堆for (int i = len;i > 1;i--) {//n-1趟的交换和建堆过程swap(A[i], A[1]);//堆顶元素和堆底元素互换HeadAdjust(1, i - 1);//把剩余的待排序元素整理成堆}
}堆排序:每一趟将堆顶元素加入有序子序列(与待排序序列中的最后一个元素交换)
并将待排序序列中再次调整为大根堆(小元素不断:下坠)
得到“递增序列”
时间复杂度:O(n)+O(nlog2n)=O(nlog2n)
(O(n)建堆,O(nlog2n)排序)
稳定性:不稳定
堆的插入删除
插入:对于小根堆,新元素放到表尾,与父结点对比,若新元素比父结点更小,则将二者互换。新元素就这样一路“上升”,直到无法继续上升为止。
删除:被删除的元素用堆底元素替代,然后让该元素不断“下坠“,直到无法下坠为止
关键字对比次数
每次“上升”调整只需对比关键字1次
每次“下坠”调整可能需要对比关键字2次,也可能只需对比1次
四、基数排序
要求:得到按关键字“递减”的有序序列
基数排序不是基于“比较”的排序算法
第一趟:以“个位”进行“分配”
第一趟“收集”结束:得到按“个位”递减排序的序列




算法思想
将整个关键字拆分为d位(组)
按照各个关键字位权重递增的次序(如:个、十、百),做d趟“分配”和“收集”,若当前处理的关键字位可能取得r个值,则需要建立r个队列
分配:顺序扫描各个元素,根据当前处理的关键字位,将元素插入相应队列。一趟分配耗时O(n)
收集:把各个队列中的结点依次出队并链接。一趟收集耗时O(r)
性能
空间复杂度 O(r)
时间复杂度 O(d(n+r)) (一趟分配O(n),一趟收集O(r))
稳定
擅长处理
1、数据元素的关键字可用方便地拆分为d组,且d较小
2、每组关键字的取值范围不大,即r较小
3、数据元素个数n较大
五、归并排序
归并:把两个或多个已经有序的序列合并成一个
2路合并 k路合并
空间复杂度O(n)
时间复杂度O(nlogn)
稳定
//B是辅助数组
const int SIZE = sizeof(A) / sizeof(A[0]);
int B[SIZE]; void Merge(int A[], int low, int mid, int high) {for (int k = low; k <= high; k++)B[k] = A[k]; int i = low, j = mid + 1, k = i;while (i <= mid && j <= high) {if (B[i] <= B[j])A[k++] = B[i++]; elseA[k++] = B[j++];}while (i <= mid) A[k++] = B[i++];while (j <= high) A[k++] = B[j++];
}void MergeSort(int A[], int low, int high) {if (low < high) {int mid = (low + high) / 2; MergeSort(A, low, mid); MergeSort(A, mid + 1, high); Merge(A, low, mid, high); }
}
相关文章:

数据结构之排序(5)
摘要:本文主要讲各种排序算法,注意它们的时间复杂度 概念 将各元素按关键字递增或递减排序顺序重新排列 评价指标 稳定性: 关键字相同的元素经过排序后相对顺序是否会改变 时间复杂度、空间复杂度 分类 内部排序——数据都在内存中 外部排序——…...

R包的安装、加载以及如何查看帮助文档
0x01 如何安装R包 一、通过R 内置函数安装(常用) 1.安装CRAN的R包 install.packages()是一个用于安装 R 包的重要函数。 语法:install.packages(pkgs, repos getOption("repos"),...) 其中: pkgs:要安…...

【YOLO学习】YOLOv3详解
文章目录 1. 网络结构1.1 结构介绍1.2 改进 2. 训练与测试过程3. 总结 1. 网络结构 1.1 结构介绍 1. 与 YOLOv2 不同的是,YOLOv3 在 Darknet-19 里加入了 ResNet 残差连接,改进之后的模型叫 Darknet-53。在 ImageNet上 实验发现 Darknet-53 相对于 ResN…...

JDK1.0主要特性
JDK 1.0,也被称为Java 1,是Java编程语言的第一个正式版本,由Sun Microsystems公司在1996年发布。JDK 1.0的发布标志着Java作为一种编程语言和平台的正式诞生,它带来了许多创新的概念和特性,对后来的软件开发产生了深远…...
)
CSS基础-盒子模型(三)
9、CSS盒子模型 9.1 CSS常用长度单位 1、px:像素; 2、em:相对元素font-size的倍数; 3、rem:相对根字体的大小,html标签即是根; 4、%:相对于父元素进行计算。 注意:CSS样…...

深度学习中的损失函数详解
深度学习中的损失函数详解 文章目录 深度学习中的损失函数详解损失函数的基础概念常见的损失函数类型及应用场景回归问题的损失函数分类问题的损失函数自定义损失函数 如何选择合适的损失函数?损失函数在深度学习中的应用 在深度学习的世界中,损失函数&a…...

系统架构设计师-下午案例题(2022年下半年)
1.试题-(共25分):阅读以下关于软件架构设计与评估的叙述在答题纸上回答问题1和问题2。 【说明】某电子商务公司拟升级其会员与促销管理系统,向用户提供个性化服务,提高用户的粘性。在项目立项之初,公司领导层一致认为本次升级的主要目标是提…...
高级图片编辑器Photopea
什么是 Photopea ? Photopea 是一款免费的在线工具,用于编辑光栅和矢量图形,支持PSD、AI 和 Sketch文件。 功能上,Photopea 和 老苏之前介绍的 miniPaint 比较像 文章传送门:在线图片编辑器miniPaint 支持的格式 复杂…...

详解zookeeper四字命令
ZooKeeper 的四字命令(Four-Letter Words, 4LW)是一组简单的管理和监控命令,方便运维人员快速获取 ZooKeeper 集群和节点的运行状态。这些命令通常用于健康检查、性能监控、节点配置查看等操作。通过这些命令,可以轻松获取关于 Zo…...

docker 进入容器运行命令
要进入正在运行的Docker容器并在其中执行命令,你可以使用docker exec命令。以下是具体步骤和示例: 1. 查看正在运行的容器 首先,确认你的容器正在运行,可以使用以下命令查看所有运行中的容器: docker ps2. 进入容器…...

一行 Python 代码能实现什么丧心病狂的功能?圣诞树源代码
手头有 109 张头部 CT 的断层扫描图片,我打算用这些图片尝试头部的三维重建。基础工作之一,就是要把这些图片数据读出来,组织成一个三维的数据结构(实际上是四维的,因为每个像素有 RGBA 四个通道)。 这个…...

mit6824-01-MapReduce详解
文章目录 MapReduce简述编程模型执行流程执行流程排序保证Combiner函数Master数据结构 容错性Worker故障Master故障 性能提升定制分区函数局部性执行缓慢的worker(slow workers) 常见问题总结回顾参考链接 MapReduce简述 MapReduce是一个在多台机器上并行计算大规模数据的软件架…...

在Docker中运行微服务注册中心Eureka
1、Docker简介: 作为开发者,经常遇到一个头大的问题:“在我机器上能运行”。而将SpringCloud微服务运行在Docker容器中,避免了因环境差异带来的兼容性问题,能够有效的解决此类问题。 通过Docker,开发者可…...

白话进程>线程>协程
文章目录 概述进程线程协程区别与联系 举个栗子进程例子线程例子协程例子区别与联系的具体体现 代码示例进程例子线程例子协程(Goroutine)例子 概述 进程、线程和协程是计算机科学中的基本概念,它们在操作系统和并发编程中扮演着重要角色。以…...
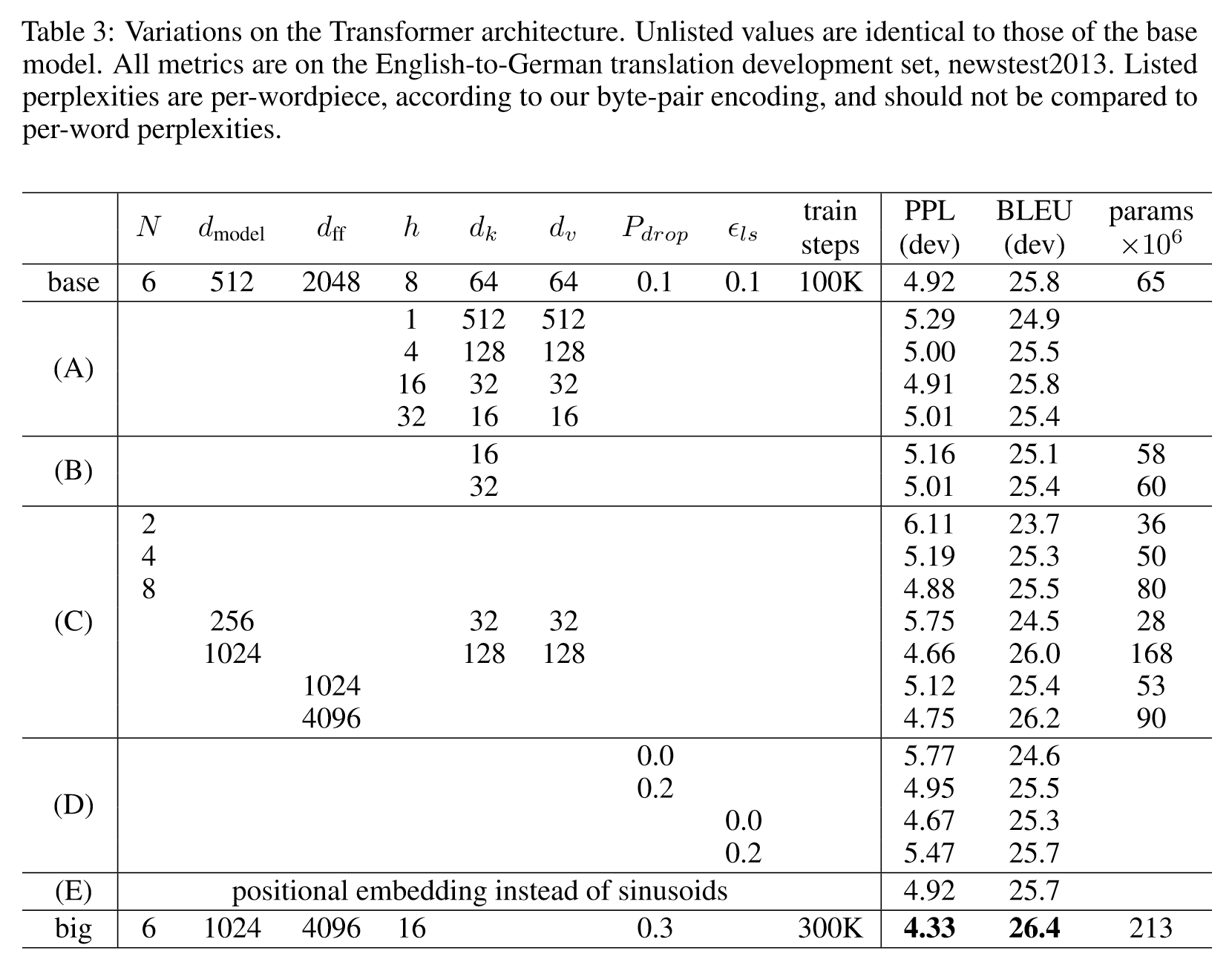
论文阅读:Attention is All you Need
Abstract 贡献: 提出了Transformer,完全基于注意力机制,摒弃了循环和卷积网络。 结果: 本模型在质量上优于现有模型,同时具有更高的并行性,并且显著减少了训练时间。 1. Introduction long short-term …...

【Linux 】文件描述符fd、重定向、缓冲区(超详解)
目录 编辑 系统接口进行文件访问 open 接口介绍 文件描述符fd 重定向 缓冲区 1、缓冲区是什么? 2、为什么要有缓冲区? 3、怎么办? 我们先来复习一下,c语言对文件的操作: C默认会打开三个输入输出流…...

Unity WebGL使用nginx作反向代理处理跨域,一些跨域的错误处理(添加了反向代理的配置依旧不能跨域)
反向代理与跨域描述 什么是跨域? 跨域(Cross-Origin Resource Sharing, CORS)是指在浏览器中,当一个网页的脚本试图从一个域名(协议、域名、端口)请求另一个域名的资源时,浏览器会阻止这种请求…...

视频转文字免费的软件有哪些?6款工具一键把视频转成文字!又快又方便!
视频转文字免费的软件有哪些?在视频制作剪辑过程中,我们经常进行视频语音识别成字幕,帮助我们更好地呈现视频内容的观看和宣传,市场上有许多免费的视频转文字软件,可以快速导入视频,进行视频内音频的文字转…...

解决DHCP服务异常导致设备无法获取IP地址的方法
DHCP在网络环境中会自动为网络中的设备分配IP地址和其他关键网络参数,可以简化网络配置过程。但是,如果DHCP服务出现异常时,设备可能无法正常获取IP地址,会影响到网络通信。 本文讲述一些办法可以有效解决DHCP服务异常导致设备无法…...

Python机器学习模型的部署与维护:版本管理、监控与更新策略
🚀 Python机器学习模型的部署与维护:版本管理、监控与更新策略 目录 💼 模型版本管理 使用DVC进行数据和模型的版本控制,确保可复现性 🔍 监控与评估 部署后的模型性能监控,使用Prometheus和Grafana进行实…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...
