算法-汉诺塔问题(Hanoi tower)
介绍
汉诺塔是源于印度的一个古老传说的小游戏,简单来说就是有三根柱子,开始的时候,第一根柱子上圆盘由大到小,自下往上排列。这个小游戏要实现的目的呢,就是要把第一根柱子上的圆盘移到第三根的柱子上去;条件呢,就是在移动过程当中不能将大的圆盘放在小的圆盘上面,我们可以利用中间第二根柱子作为桥梁来承接我们要移动的圆盘。
而在这个传说当中,一共有64块圆盘,假设我们使用递归的方法,我们也得用18446744073709551615的步数来实现我们的目的,换算成时间呢,我们得花5845.42亿年来实现这个过程。
算法思路
实现这个小游戏的算法思路是什么呢?
我们一定要将最大的那块圆盘放到C柱那里去,那么我们的目的就很明确,我们倒着思考一下,最后那几步的时候,我们是要将上面的n-1块圆盘移动到中间的柱子上,最后再将n-1块圆盘放到C柱上的。

假设我们这里有三块圆盘,我们先将A盘上的两块小圆盘移到B盘上去

再将A柱上最大的圆盘移动到C柱上

再将B柱上的圆盘放回C住上,最后大功告成

那在这一步的前一步呢,那不就是n-2块了吗,对于前面的步骤,都是和最后的类似,那最后一步我们走了几步呢?假设我们有一个表达式能描述移动的步数,那么
为什么会有这个表达式呢,我们先移动了n-1块盘到B柱,再将n-1块盘到C柱,这里我们就可以得到,我们还将最下面的那个盘子放到了C盘这里,所以我们在这里得加一。
最后我们可以得到步数的结果为
其它方法
美国学者曾提出过一种更为简洁的方法:首先把三根柱子按顺序排成品字型,把所有的圆盘按从大到小的顺序放在柱子A上,根据圆盘的数量确定柱子的排放顺序:
- 若n为偶数,按顺时针方向依次摆放 A B C
- 若n为奇数,按顺时针方向依次摆放 A C B
步骤
-
按顺时针方向把圆盘1从现在的柱子移动到下一根柱子,即当n为偶数时,若圆盘1在柱子A,则把它移动到B;若圆盘1在柱子B,则把它移动到C;若圆盘1在柱子C,则把它移动到A。
-
接着,把另外两根柱子上可以移动的圆盘移动到新的柱子上。即把非空柱子上的圆盘移动到空柱子上,当两根柱子都非空时,移动较小的圆盘。这一步没有明确规定移动哪个圆盘,你可能以为会有多种可能性,其实不然,可实施的行动是唯一的。
-
反复进行⑴⑵操作,最后就能按规定完成汉诺塔的移动。
代码实现
python
def f(n):if n==0:return 0else:return 2*f(n-1)+1
x=int(input("请输入片的个数:"))
print("需要移动",f(x),"次")def hanoi(n, a, b, c):if n == 1:print(a, '-->', c)else:hanoi(n - 1, a, c, b)print(a, '-->', c)hanoi(n - 1, b, a, c)
# 调用
hanoi(5, 'A', 'B', 'C')cpp
#include <iostream> using namespace std; void hanoi(int n, char source, char help, char target){static int step = 0; if (n == 1)std::cout << (++step) << ": " << source << "---->" << target << endl; else{// move n-1 disks from source to help hanoi(n-1, source, target, help); std::cout <<(++step) << ": " << source << "---->" << target << endl; hanoi(n-1, help, source, target);}
}
int main(void){hanoi(10, 'a', 'b', 'c');return 0;
}
C
#include <stdio.h>
#include <windows.h>
void Hanoi(int n, char a,char b,char c);
void Move(int n, char a, char b);
int count;
int main()
{int n=8;printf("汉诺塔的层数:\n");scanf(" %d",&n);Hanoi(n, 'A', 'B', 'C');Sleep(20000);return 0;
}
void Hanoi(int n, char a, char b, char c)
{if (n == 1){Move(n, a, c);}else{Hanoi(n - 1, a, c, b);Move(n, a, c);Hanoi(n - 1, b, a, c);}
}
void Move(int n, char a, char b)
{count++;printf("第%d次移动 Move %d: Move from %c to %c !\n",count,n,a,b);
}相关文章:
算法-汉诺塔问题(Hanoi tower)
介绍 汉诺塔是源于印度的一个古老传说的小游戏,简单来说就是有三根柱子,开始的时候,第一根柱子上圆盘由大到小,自下往上排列。这个小游戏要实现的目的呢,就是要把第一根柱子上的圆盘移到第三根的柱子上去;…...
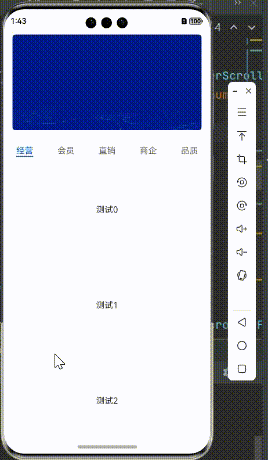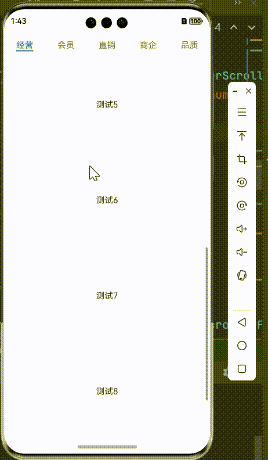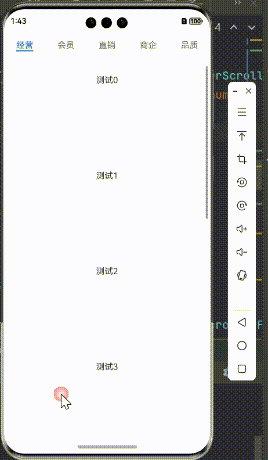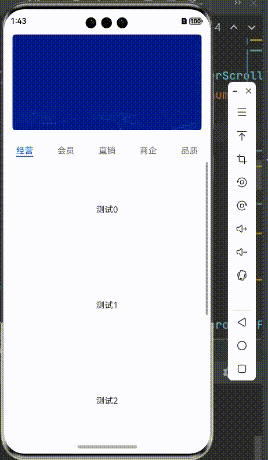
HarmonyOS鸿蒙 Next 实现协调布局效果
HarmonyOS鸿蒙 Next 实现协调布局效果 假期愉快! 最近大A 的涨势实在是红的让人晕头转向,不知道各位收益如何,这会是在路上,还是已经到目的地了? 言归正传,最近有些忙,关于鸿蒙的实践系列有些脱节了,…...

【自然语言处理】(1) --语言转换方法
文章目录 语言转换方法一、统计语言模型1. 词向量转换2. 统计模型问题 二、神经语言模型1. 词向量化2. 维度灾难3. 解决维度灾难4. embedding词嵌入5. Word2Vec技术5.1 连续词袋模型(CBOW)5.2 跳字模型(Skip-gram) 总结 语言转换方…...

叉车防撞系统方案,引领安全作业新时代
在现代工业的舞台上,叉车如同忙碌的“搬运工”,在仓储和制造环境中发挥着不可或缺的作用。然而,随着叉车使用频率的不断攀升,安全事故也如影随形,给企业带来经济损失的同时,更严重威胁着操作人员的生命安全…...

Nginx的核心架构和设计原理
Nginx 是一个免费的、开源的、高性能 Http 服务器和反向代理。Nginx 的架构设计是为了提供高性能、稳定性和可扩展性。 Nginx 的主要架构组件和工作原理: 1、Master 进程:Nginx 的运行始于一个 master 进程,它负责管理所有的工作进程。mast…...

leetcode35--搜索插入位置--二分查找刷题
搜索插入位置 一共会出现下面四种情况: 目标值在数组所有元素之前 目标值等于数组中某一个元素 目标值插入数组中的位置 目标值在数组所有元素之后 首先在二分查找的代码之前处理掉目标值在数组所有元素之前和之后的情况如果目标值在数组中的某个位置,…...

Django对接支付宝沙箱环境(2024年9月新测有效)
1、申请沙箱环境 #需要填一些个人信息 https://opendocs.alipay.com/ 2、使用支付宝登入,并进入控制台,进入开发者工具推荐-->沙箱 3、获取基本信息 主要是APPID,和支付宝网关地址 4、生成应用私钥和应用公钥和支付宝公钥 上面的接口加签方式选择…...

【MySQL】-- 库的操作
文章目录 1. 查看数据库1.1 语法 2. 创建数据库2.1 语法2.2 示例2.2.1 创建一个名为java114的数据库2.2.2 创建数据库java114,如果数据库不存在则创建2.2.3 查看警告信息 3. 字符集编码和校验(排序)规则3.1 查看数据库支持的字符集编码3.2 查…...

linux桌面软件(wps)内嵌到主窗口后的关闭问题
程序测试环境是:slackware系统,属于linux系统,有桌面(Xface Session)。系统镜像是:slackware64-15.0-install-dvd.iso。qt、c代码实现。 问题描述:延续上一篇文章,将wps软件窗口内嵌…...

WindowsTerminal 美化-壁纸随机更换
目录 一. 相关网址二. 壁纸随机更换思路三. 指定 WindowsTermina 壁纸路径四. 编写脚本,随机替换壁纸4.1 powershell脚本4.2 .bat批处理脚本 四. 配置定时任务,添加触发器五. 效果 一. 相关网址 官方下载 Windows Terminal 官方Github微软商店 美化 Oh …...

iOS 多次获取图片主题色不一样
一个需求中,要求获取图片的主题色 代码如下 -(void)kk_getImage:(UIImage *)image fetchthemeColor:(void(^)(UIColor *color))callBack {dispatch_async(dispatch_get_global_queue(DISPATCH_QUEUE_PRIORITY_DEFAULT, 0), ^{// 第一步 先把图片缩小 加快计算速度.…...

UE5 武器IK瞄准系统
创建空项目 创建基础蓝图类My_GameMode,My_HUD,My_PlayChar,My_PlayController 项目设置地图模式 近裁平面 0.1 My_PlayChar蓝图中添加摄像机,角色骨骼网格体,武器骨骼网格体 编辑角色骨骼,预览控制器使用特定动画,动画选择ANM_ark-47-Idle hand_r 添加插槽WeaponMes…...
①EtherCAT转ModbusTCP, EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关
EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关https://item.taobao.com/item.htm?ftt&id822721028899 协议转换通信网关 EtherCAT 转 ModbusTCP GW系列型号 MS-GW15 简介 MS-GW15 是 EtherCAT 和 Modbus TCP 协议转换网关,为用户提供一种 …...

在macOS上进行开发环境配置与应用开发详细的配置指南
在macOS上进行开发环境配置与应用开发,需要遵循一系列步骤来确保你的开发环境既高效又稳定。以下是一个详细的配置指南,涵盖了从安装基本工具到创建应用的整个过程。 1. 安装和更新macOS 首先,确保你的macOS是最新版本。更新系统可以提供更…...

JavaScript 事件处理基础
在网页中添加事件监听器,可以通过JavaScript代码来实现。 要处理用户的交互事件,需要先选择要添加事件监听器的元素,可以使用document.querySelector()或document.getElementById()等方法来获取元素。 然后,使用addEventListene…...

WordPress响应式Git主题响应式CMS主题模板
兼容 IE9、谷歌 Chrome 、火狐 Firefox 等主流浏览器 扁平化的设计加响应式布局,兼容电脑、和各个尺寸手机的完美响应 主题设置面板新增多种AD位,PC端和移动设备各不相同 在主题设置选项中就可以进行基本的SEO设置:首页、分类、文章等页面…...

Solidity 设计模式:实现灵活与可扩展的智能合约架构
Solidity 作为以太坊智能合约的主要编程语言,拥有许多独特的设计模式,这些模式帮助开发者实现更加灵活、可扩展和安全的合约架构。设计模式不仅能够简化开发过程,还能减少常见的编程错误,并提高智能合约的可维护性和可升级性。本文…...

房屋水电费:重新布局,重构JS代码
<!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>房租水电费</title><script type"…...

Jmeter生成JWT token
JWT简介 JWT官网:https://jwt.io/ JSON Web令牌(JWT)是一个开放标准(RFC 7519),它定义了一种紧凑而自包含的方式,用于在各方之间以JSON对象的形式安全地传输信息。此信息可以验证和信任&#x…...

STM32的ADC技术详解
ADC(Analog-to-Digital Converter,模数转换器) 是将连续的模拟信号转换为离散的数字信号的关键组件。在STM32系列微控制器中,ADC广泛应用于传感器数据采集、信号处理和控制系统等领域。本文将详细介绍STM32的ADC技术,包…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
