使用 NVIDIA H100 上的 Azure 机密计算释放隐私保护 AI 的潜力
通过 NVIDIA H100 上的 Azure 机密计算释放隐私保护 AI 的潜力
文章目录
- 前言
- 一、机密计算
- 二、使用 NVIDIA H100 Tensor Core GPU 的 Azure 机密计算
- 1. 安全功能
- 2. 可扩展性和可编程性
- 三、场景
- 1. 模型机密性
- 2. 推理/提示机密性
- 3. 使用私有数据进行微调
- 4. 多方培训
- 结论


前言
这是 AI 技术取得突破的一年。ChatGPT 和 Bing Chat 等大型语言模型 (LLM) 在大量公共数据上进行了训练,展示了从写诗到生成计算机程序的一系列令人印象深刻的技能,尽管它们不是为解决任何特定任务而设计的。
但是,即使一些用户可能已经习惯与聊天机器人分享个人信息(例如他们的社交媒体资料和病史)并寻求推荐,但重要的是要记住,这些 LLMs 仍处于相对早期的开发阶段,通常不推荐使用用于复杂的咨询任务,例如医疗诊断、财务风险评估或业务分析。能够可靠地执行这些任务的模型需要在模型架构(例如,根据图像、音频和视频等多模型数据进行训练的能力)和专业高质量训练数据的来源方式方面进行创新。
可用于训练下一代模型的数据已经存在,但它既是私人的(根据政策或法律),又分散在许多独立实体中:医疗实践和医院、银行和金融服务提供商、物流公司、咨询公司…这些参与者中的少数最大参与者可能有足够的数据来创建自己的模型,但处于 AI 创新前沿的初创公司无法访问这些数据集。
一、机密计算
机密计算是一项基础技术,可以解锁对敏感数据集的访问,同时满足数据提供商和广大公众的隐私和合规性问题。通过机密计算,数据提供商可以授权将其数据集用于特定任务(通过认证验证),例如训练或微调商定的模型,同时保持数据机密。最终用户可以通过检查推理服务不会出于未经授权的目的收集其数据来保护其隐私。模型提供商可以验证为其模型提供服务的推理服务运营商无法提取模型的内部架构和权重。
与使用单个组织的数据训练的相同模型相比,机密计算可以使多个组织将其数据集汇集在一起,以更高的准确性和更低的
相关文章:

使用 NVIDIA H100 上的 Azure 机密计算释放隐私保护 AI 的潜力
通过 NVIDIA H100 上的 Azure 机密计算释放隐私保护 AI 的潜力 文章目录 前言一、机密计算二、使用 NVIDIA H100 Tensor Core GPU 的 Azure 机密计算1. 安全功能2. 可扩展性和可编程性三、场景1. 模型机密性2. 推理/提示机密性3. 使用私有数据进行微调4. 多方培训结论前言 这是…...

目标检测与图像分类:有什么区别?各自的使用场景是什么?
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 《------往期经典推…...

Lua 数据类型
Lua 数据类型 Lua 是一种轻量级的编程语言,因其简单性和灵活性而广受欢迎。在 Lua 中,数据类型是编程的基础,它们决定了变量能够存储哪种类型的数据。Lua 的数据类型可以分为以下几个类别: 1. nil nil 是 Lua 中的一个特殊类型…...

复现文章:R语言复现文章画图
文章目录 介绍数据和代码图1图2图6附图2附图3附图4附图5附图6 介绍 文章提供画图代码和数据,本文记录 数据和代码 数据可从以下链接下载(画图所需要的所有数据): 百度云盘链接: https://pan.baidu.com/s/1peU1f8_TG2kUKXftkpYq…...

东方仙盟——软件终端架构思维———未来之窗行业应用跨平台架构
一、创生.前世今生 在当今的数字化时代,我们的服务覆盖全球,拥有数亿客户。然而,这庞大的用户规模也带来了巨大的挑战。安全问题至关重要,任何一处的漏洞都可能引发严重的数据泄露危机。网络带宽时刻面临考验,稍有不足…...

支持向量机(SVM)基础教程
一、引言 支持向量机(Support Vector Machine,简称SVM)是一种高效的监督学习算法,广泛应用 于分类和回归分析。SVM以其强大的泛化能力、简洁的数学形式和优秀的分类效果而备受机器学 习领域的青睐。 二、SVM基本原理 2.1 最大间…...

Python小示例——质地不均匀的硬币概率统计
在概率论和统计学中,随机事件的行为可以通过大量实验来研究。在日常生活中,我们经常用硬币进行抽样,比如抛硬币来决定某个结果。然而,当我们处理的是“质地不均匀”的硬币时,事情就变得复杂了。质地不均匀的硬币意味着…...

京东web 京东e卡绑定 第二部分分析
声明 本文章中所有内容仅供学习交流使用,不用于其他任何目的,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关! 有相关问题请第一时间头像私信联系我删…...

【数据结构与算法】Greedy Algorithm
1) 贪心例子 称之为贪心算法或贪婪算法,核心思想是 将寻找最优解的问题分为若干个步骤每一步骤都采用贪心原则,选取当前最优解因为没有考虑所有可能,局部最优的堆叠不一定让最终解最优 贪心算法是一种在每一步选择中都采取在当前状态下最好…...

Ubuntu22.04之mpv播放器高频快捷键(二百七十)
简介: CSDN博客专家、《Android系统多媒体进阶实战》一书作者 新书发布:《Android系统多媒体进阶实战》🚀 优质专栏: Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏: 多媒体系统工程师系列【…...

新闻推荐系统:Spring Boot的可扩展性
6系统测试 6.1概念和意义 测试的定义:程序测试是为了发现错误而执行程序的过程。测试(Testing)的任务与目的可以描述为: 目的:发现程序的错误; 任务:通过在计算机上执行程序,暴露程序中潜在的错误。 另一个…...

目录工具类 - C#小函数类推荐
此文记录的是目录工具类。 /***目录工具类Austin Liu 刘恒辉Project Manager and Software DesignerE-Mail: lzhdim163.comBlog: http://lzhdim.cnblogs.comDate: 2024-01-15 15:18:00***/namespace Lzhdim.LPF.Utility {using System.IO;/// <summary>/// The Objec…...

速盾:如何判断高防服务器的防御是否真实?
随着网络攻击日益增多和攻击手段的不断升级,保护网络安全变得越来越重要。高防服务器作为一种提供网络安全保护的解决方案,受到了越来越多的关注。然而,对于用户来说,如何判断高防服务器的防御是否真实,是否能够真正保…...

MySQL连接查询:联合查询
先看我的表结构 emp表 联合查询的关键字(union all, union) 联合查询 基本语法 select 字段列表 表A union all select 字段列表 表B 例子:将薪资低于5000的员工, 和 年龄大于50 岁的员工全部查询出来 第一种 select * fr…...

Gitea 数据迁移
一、从 Windows 迁移 Gitea 1. 备份 Gitea 数据 1.1 备份仓库文件 在 Windows 中,Gitea 仓库文件通常位于 C:\gitea\data\repositories。你可以使用压缩工具将该目录打包: 1.)右键点击 C:\gitea\data\repositories 目录,选择 “…...

MySQL 绪论
数据库相关概念 数据库(DB):存储数据的仓库数据库管理系统(DBMS):操纵和管理数据库的大型软件SQL:操纵关系型数据库的编程语言,定义了一套操作关系型数据库的统一标准主流的关系型数…...

什么是 HTTP Get + Preflight 请求
当在 Chrome 开发者工具的 Network 面板中看到 GET Preflight 的 HTTP 请求方法时,意味着该请求涉及跨域资源共享 (CORS),并且该请求被预检了。理解这种请求的背景,主要在于 CORS 的工作机制和现代浏览器对安全性的管理。 下面是在 Chrome …...

(JAVA)开始熟悉 “二叉树” 的数据结构
1. 二叉树入门 符号表的增删查改操作,随着元素个数N的增多,其耗时也是线性增多的。时间复杂度都是O(n),为了提高运算效率,下面将学习 树 这种数据结构 1.1 树的基本定义 树是我们计算机中非常重要的一种数据结构…...
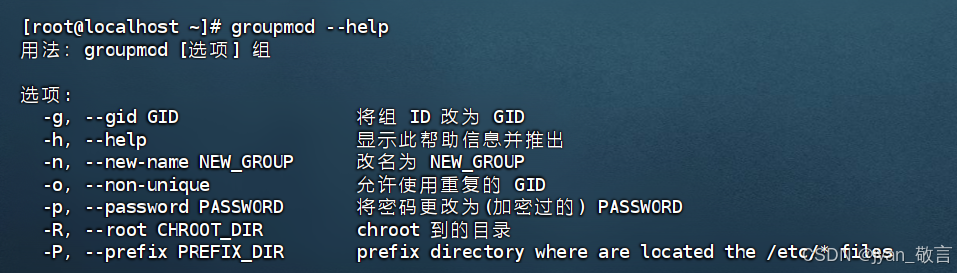
【Linux】Linux命令与操作详解(一)文件管理(文件命令)、用户与用户组管理(创建、删除用户/组)
文章目录 一、前言1.1、Linux的文件结构是一颗从 根目录/ 开始的一个多叉树。1.2、绝对路径与相对路径1.3、命令的本质是可执行文件。1.4、家目录 二、文件管理2.1、文件操作1、pwd2、ls3、cd4、touch5、mkdir6、cp7、rm8、mv9、rmdir 2.2、查看文件1、cat2、more3、less4、hea…...
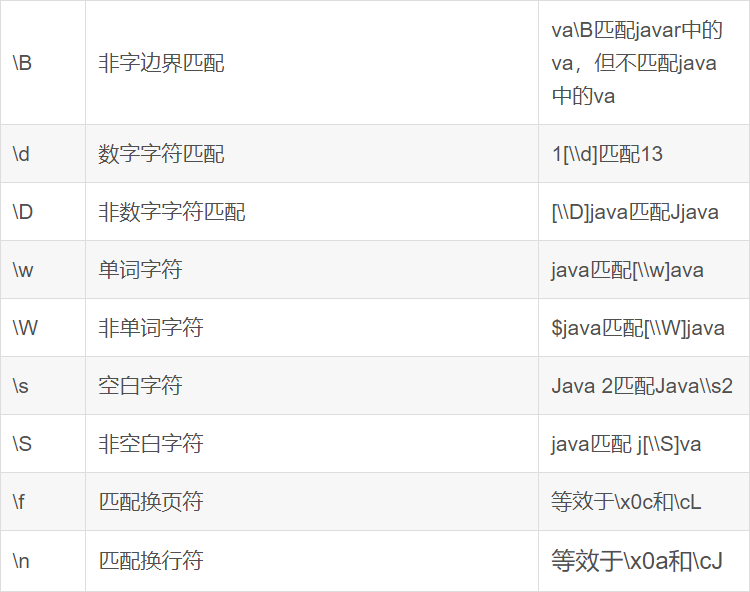
Hadoop大数据入门——Hive-SQL语法大全
Hive SQL 语法大全 基于语法描述说明 CREATE DATABASE [IF NOT EXISTS] db_name [LOCATION] path; SELECT expr, ... FROM tbl ORDER BY col_name [ASC | DESC] (A | B | C)如上语法,在语法描述中出现: [],表示可选,如上[LOCATI…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
