二叉树搜索树 AVL树
文章目录
- 1. 二叉搜索树
- 1.1 二叉搜索树概念
- 1.2 二叉搜索树操作
- 1.3 二叉搜索树的实现
- 1.4 二叉搜索树的应用
- 1.5 二叉搜索树的性能分析
- 2. AVL 树
- 2.1 AVL树的概念
- 2.2 AVL树节点的定义
- 2.3 AVL树的插入
- 2.4 AVL树的旋转
- 2.5 AVL树的验证
- 2.7 AVL树的性能
- 3. 具体代码实现区
- 3.1 二叉搜索树的代码实现
- 3.2 AVL树的具体代码实现
1. 二叉搜索树
1.1 二叉搜索树概念
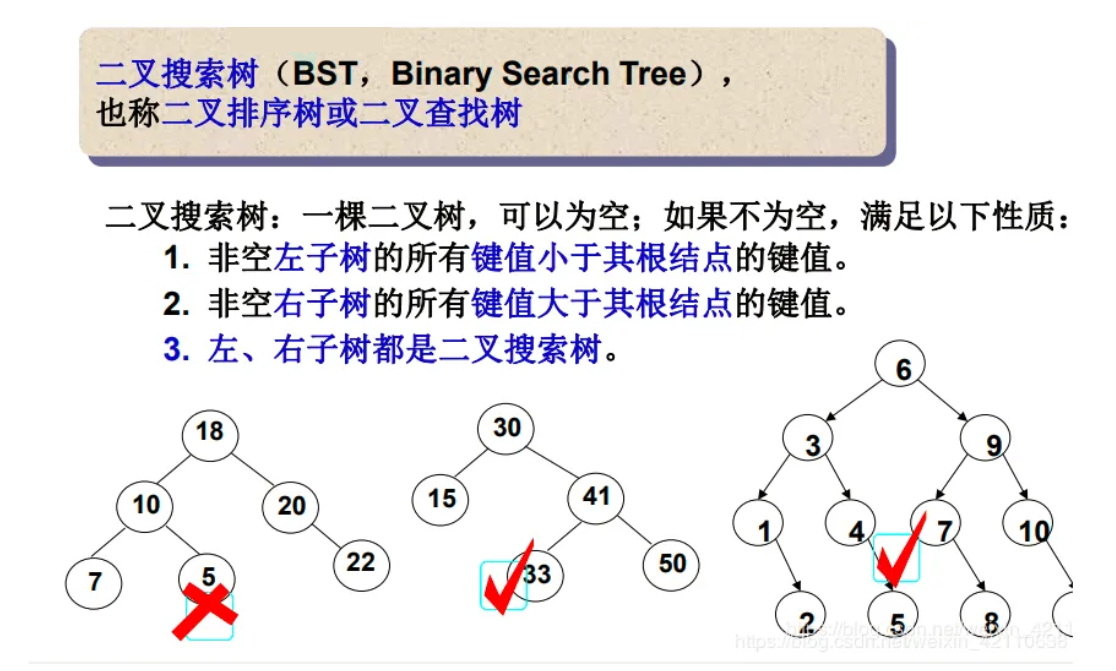
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
1.2 二叉搜索树操作
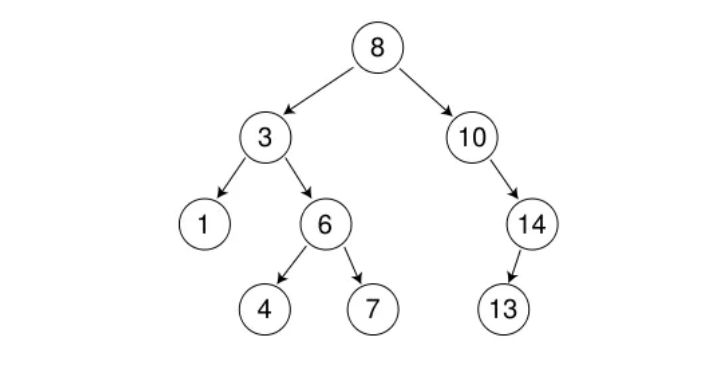
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
-
二叉搜索树的查找
a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
b、最多查找高度次,走到到空,还没找到,这个值不存在。 -
二叉搜索树的插入
插入的具体过程如下:
a. 树为空,则直接新增节点,赋值给root指针
b. 树不空,按二叉搜索树性质查找插入位置,插入新节点
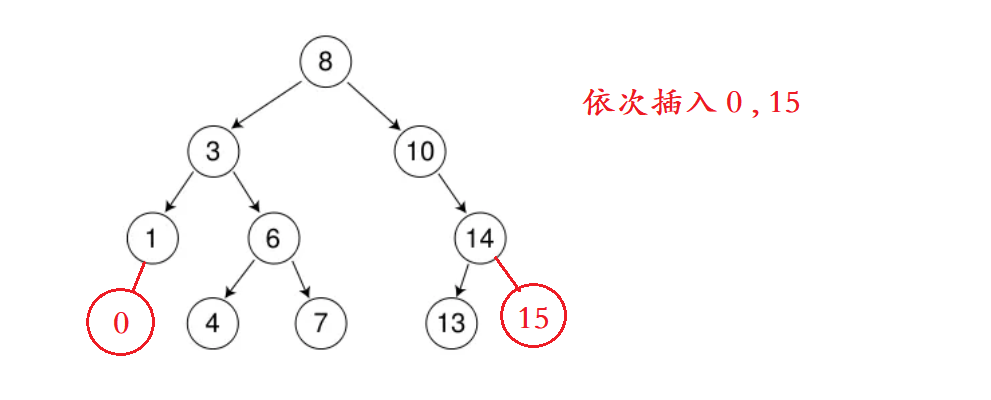
- 二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程
如下:
-
情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除
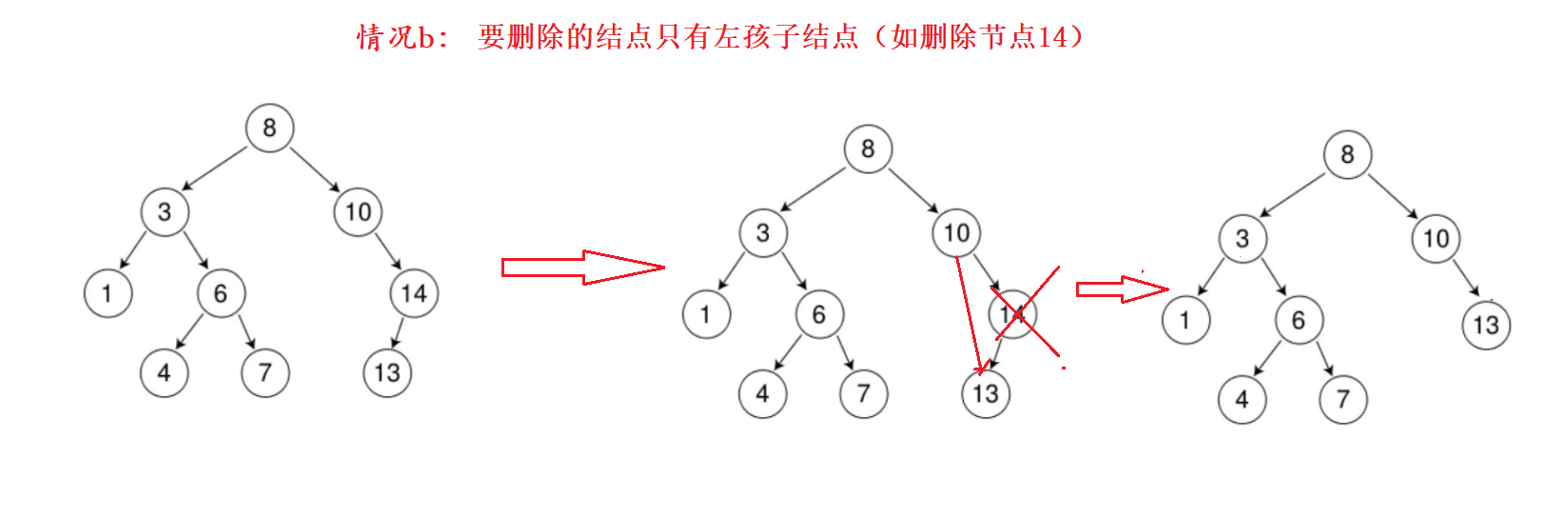
-
情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除
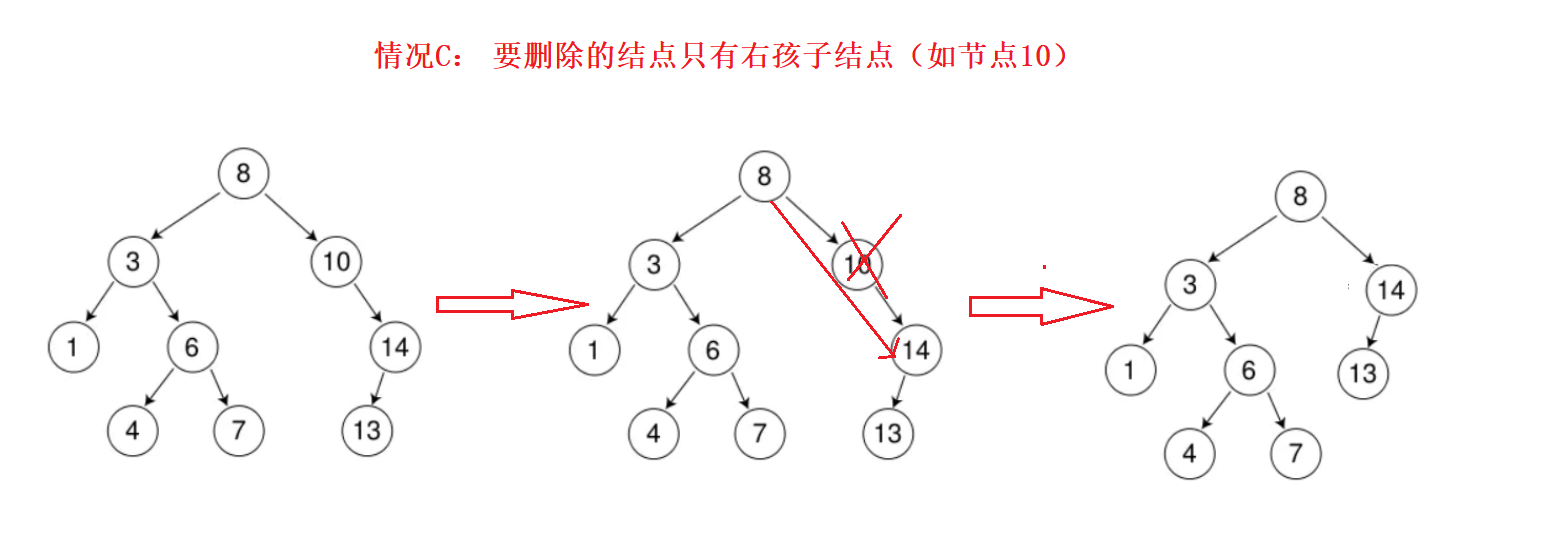
-
情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题–替换法删除
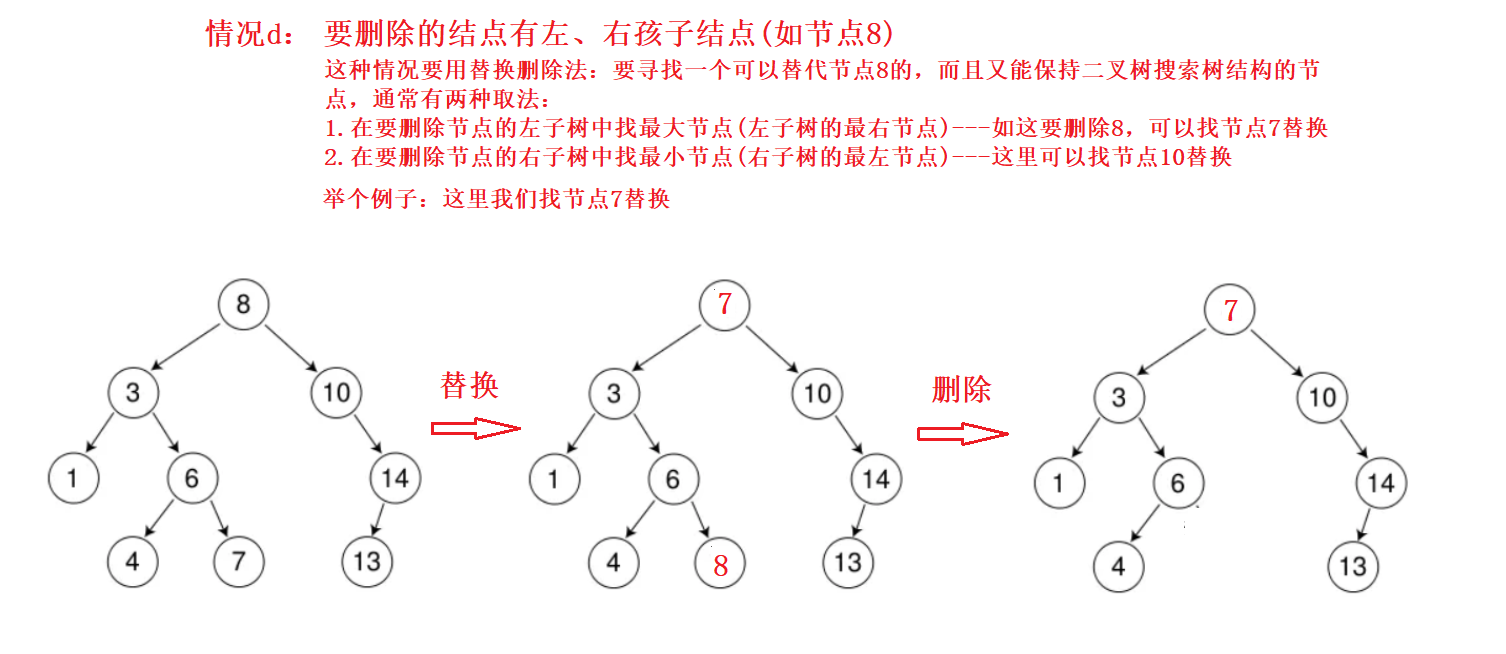
1.3 二叉搜索树的实现
跳转到下面—》代码区
1.4 二叉搜索树的应用
-
K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
-
KV模型:每一个关键码key,都有与之对应的值Value,即<Key, Value>的键值对。该种方式在现实生活中非常常见:(C++库中就有一个pair,就是KV模型,下面将会学习)
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文<word, chinese>就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是<word, count>就构成一种键值对
// 改造二叉搜索树为KV结构
template<class K, class V>
struct BSTNode
{BSTNode(const K& key = K(), const V& value = V()): _pLeft(nullptr), _pRight(nullptr), _key(key), _Value(value){}BSTNode<T>* _pLeft;BSTNode<T>* _pRight;K _key;V _value
};
template<class K, class V>
class BSTree
{typedef BSTNode<K, V> Node;typedef Node* PNode;
public:BSTree() : _pRoot(nullptr){}PNode Find(const K& key);bool Insert(const K& key, const V& value)bool Erase(const K& key)
private:PNode _pRoot;
}
1.5 二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
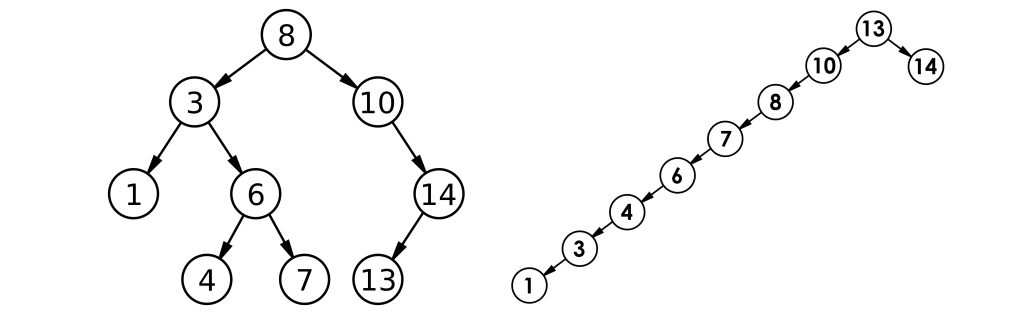
- 最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:log2Nlog_2 Nlog2N
- **最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N2\frac{N}{2}2N **
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?
那么AVL树和红黑树就可以上场了。
2. AVL 树
2.1 AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
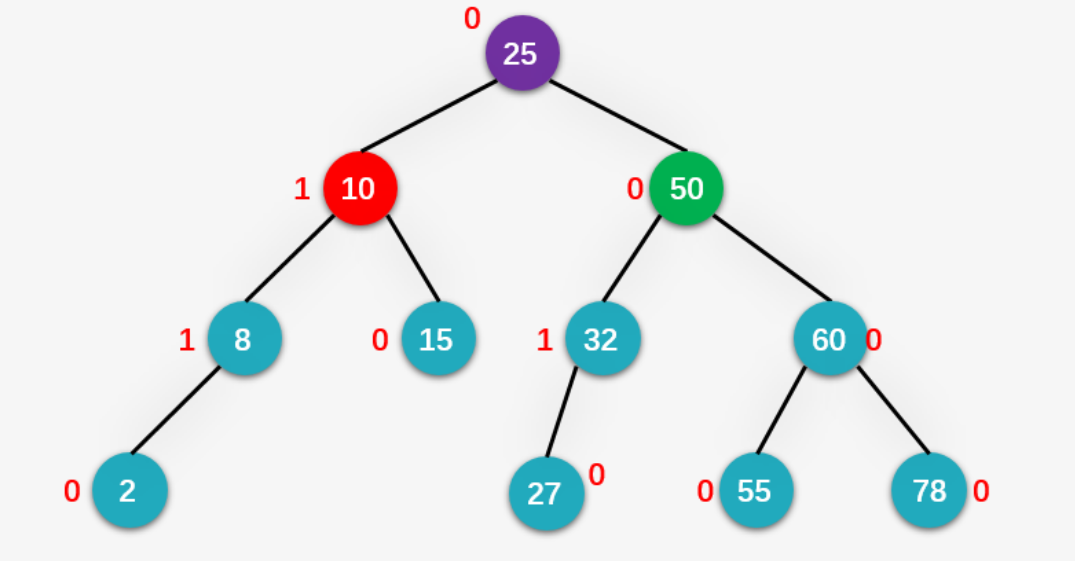
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log2n)O(log_2 n)O(log2n),搜索时间复杂度O(log2nlog_2 nlog2n)。
2.2 AVL树节点的定义
AVL树节点的定义:
采用的是三叉链结构
template<class T>
struct AVLTreeNode
{T data;AVLTreeNode<T>*_left;// 该节点的左孩子AVLTreeNode<T>* _right;// 该节点的右孩子AVLTreeNode<T>* _parent;// 该节点的双亲int _bf;// 该节点的平衡因子----可以用右子树的高度-左子树的高度AVLTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};2.3 AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。
那么AVL树的插入过程可以分为两步:
-
按照二叉搜索树的方式插入新节点
-
调整节点的平衡因子
(具体代码实现在看下面的代码)
跳转到下面–》代码区
2.4 AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
- 新节点插入较高左子树的左侧—左左:右单旋
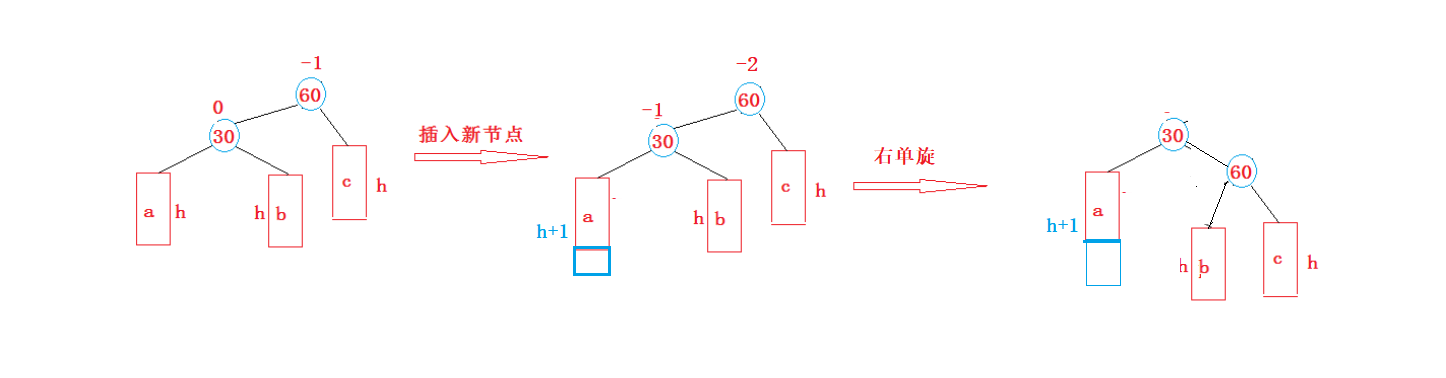
- 新节点插入较高右子树的右侧—右右:左单旋
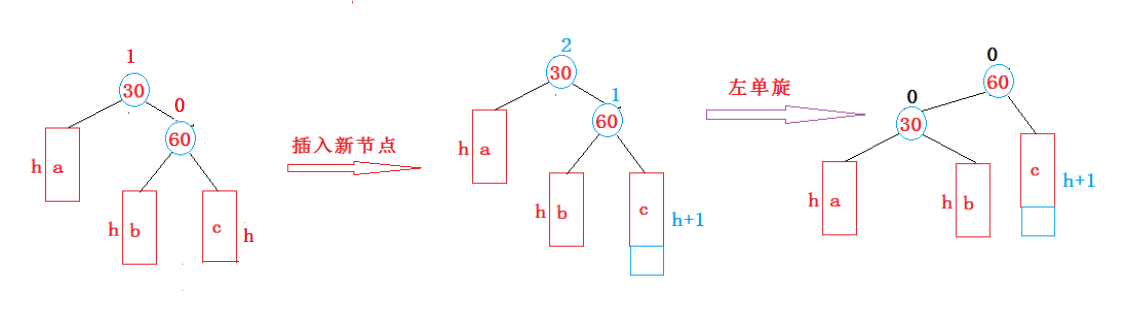
- 新节点插入较高左子树的右侧—左右:先左单旋再右单旋
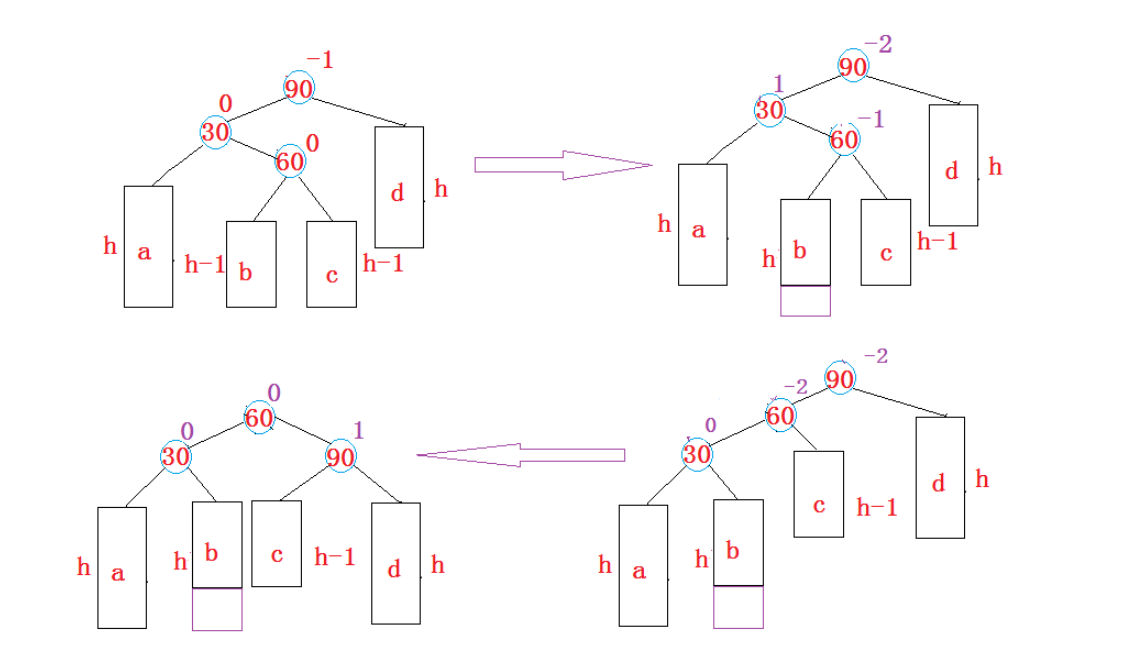
将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再考虑平衡因子的更新。
一个简单的例子
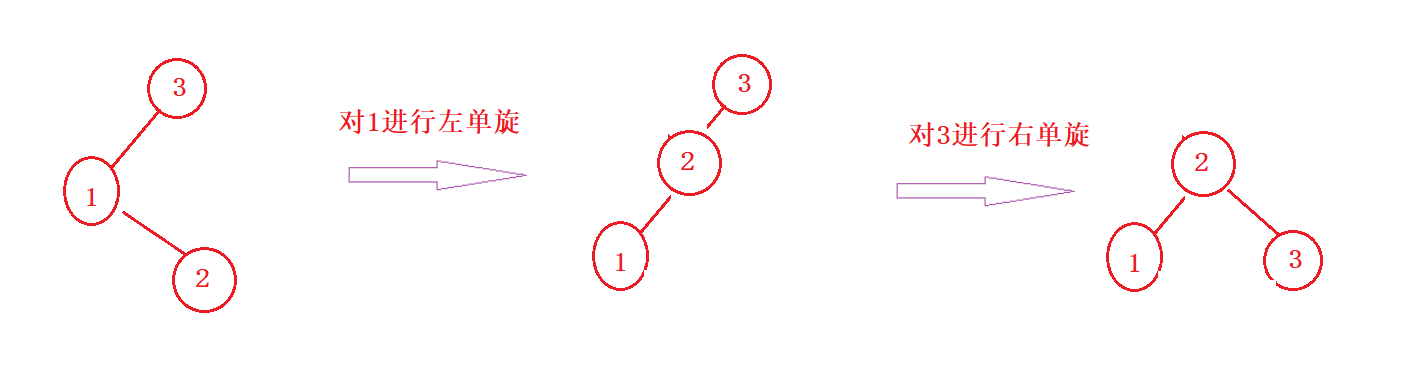
- 新节点插入较高右子树的左侧—右左:先右单旋再左单旋
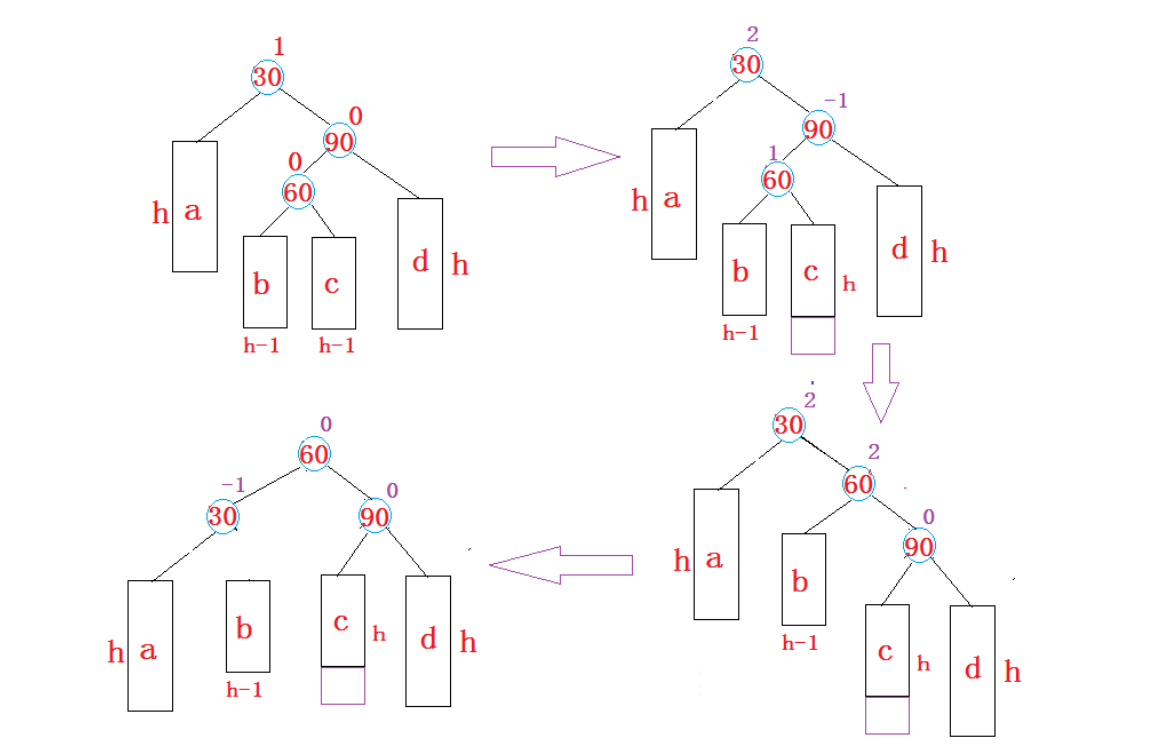
参考右左双旋。
一个简单的例子:
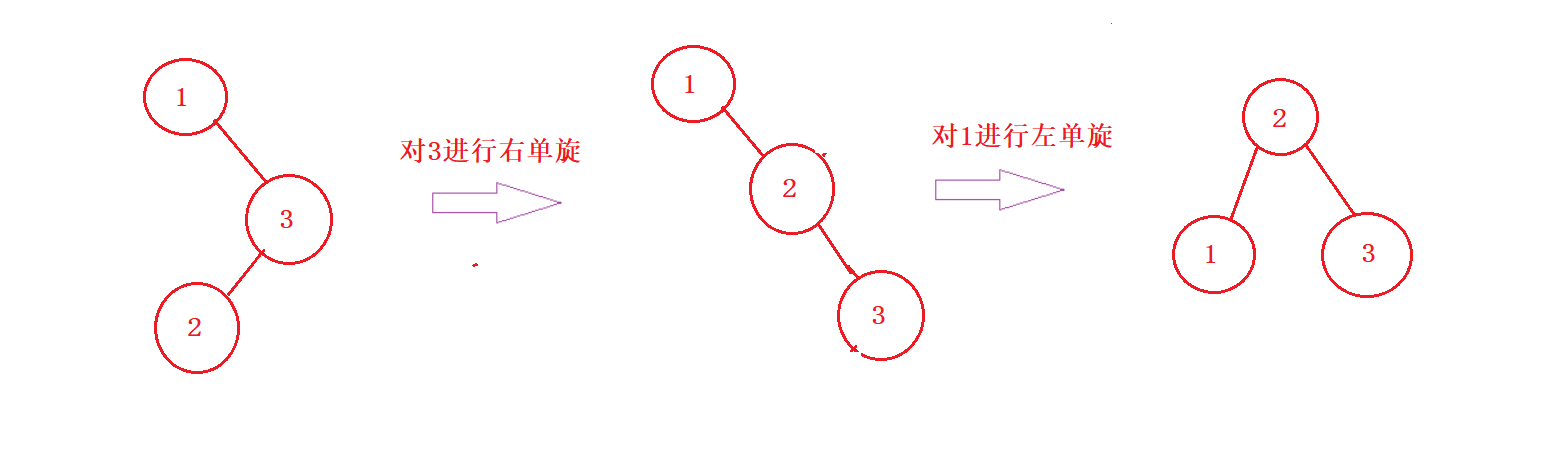
总结:
假如以pParent为根的子树不平衡,即pParent的平衡因子为2或者-2,分以下情况考虑
-
pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR
- 当pSubR的平衡因子为1时,执行左单旋
- 当pSubR的平衡因子为-1时,执行右左双旋
-
pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL
- 当pSubL的平衡因子为-1是,执行右单旋
- 当pSubL的平衡因子为1时,执行左右双旋
旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新。
2.5 AVL树的验证
AVL树的代码这么复杂,那我们该如何确认我们写的代码是否有问题呢?
这时候我们可以写一个程序进行验证!
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
-
验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树 -
验证其为平衡树
每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
节点的平衡因子是否计算正确
bool IsBalanceTree(Node* root)
{if (root == nullptr)//空树叶是AVL树return true;// 计算root节点的平衡因子:即root左右子树的高度差int leftHeight = GetTreeHeight(root->_left);int rightHeight = GetTreeHeight(root->_right);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者// pRoot平衡因子的绝对值超过1,则一定不是AVL树if (diff != root->_bf || diff>1 || diff<-1){std::cout << root->_val << "->该节点平衡因子错误!" << "root->_bf:"<< root->_bf << "实际_bf" << diff << std::endl;return false;}// root的左和右如果都是AVL树,则该树一定是AVL树return IsBalanceTree(root->_left) && IsBalanceTree(root->_right);
}
-
验证用例
可以结合上述代码按照以下的数据次序,自己动手画AVL树的创建过程,验证代码是否有漏洞。
- 常规场景1
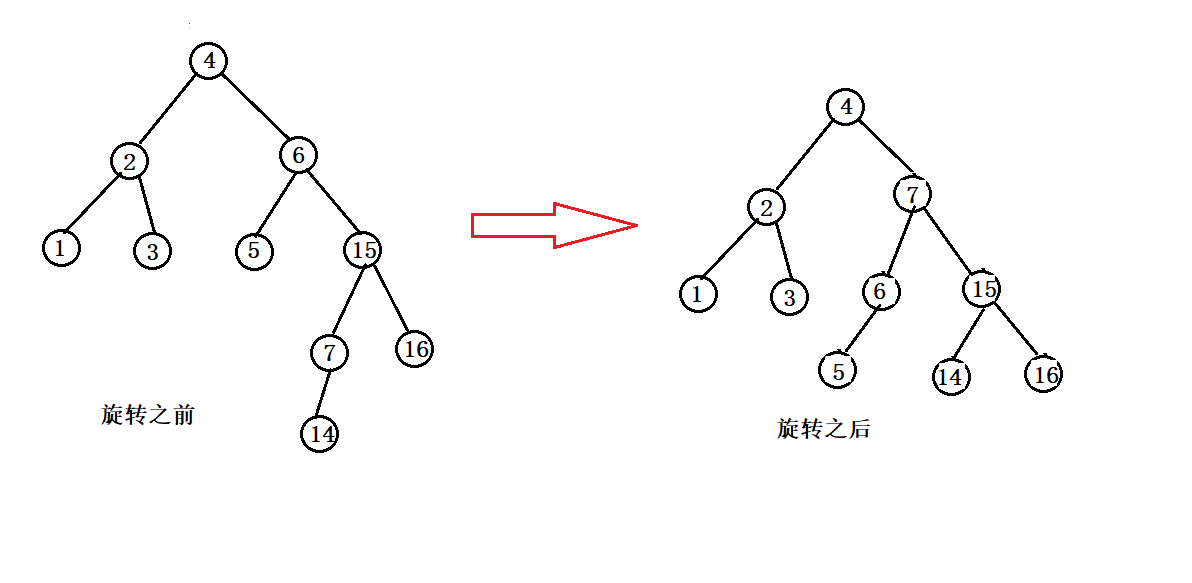
{16, 3, 7, 11, 9, 26, 18, 14, 15} - 特殊场景2
{4, 2, 6, 1, 3, 5, 15, 7, 16, 14}
2.7 AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即log2(N)log_2 (N)log2(N)。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
3. 具体代码实现区
3.1 二叉搜索树的代码实现
#pragma once
#include <iostream>
#include <cassert>
using namespace std;namespace hdm
{/*Binary Search Tree---二叉搜索树或二叉排序树*/template<class T>struct BSTreeNode{T _val;BSTreeNode<T>* _left;//左孩子BSTreeNode<T>* _right;//右孩子BSTreeNode(const T& val = T()):_val(val), _left(nullptr), _right(nullptr){}};template<class T>class BSTree{public:typedef BSTreeNode<T> Node;Node* find(const T& x){Node* cur = _root;while (cur){if (cur->_val > x)//比cur小往左子树找{cur = cur->_left;}else if (cur->_val < x)//比cur大往右子树找{cur = cur->_right;}else//相等即返回{return cur;}}return nullptr;}bool insert(const T& x){if (_root == nullptr)//_root==nullptr说明为空树{_root = new Node(x);return true;}Node* cur = _root;Node* parent = cur;//记录父节点用于连接新节点while (cur){//cur往子树走的同时记录子树的父节点if (cur->_val > x)//比cur小往左子树找{parent = cur;cur = cur->_left;}else if (cur->_val < x)//比cur大往右子树找{parent = cur;cur = cur->_right;}else//进入else说明cur->_val==x,表示已经存在该节点,不需要插入,返回false表示插入失败{return false;}}//程序走到这说明cur=nullptr,最后x就应该要插入在parent的下面,至于是插入左边还是右边//具体看x与parent->_val 之间值的关系if (parent->_val > x)//如果x的值小于parent就往左边插入{parent->_left = new Node(x);}else//如果x的值大于parent就往右边插入{parent->_right = new Node(x);}return true;}bool erase(const T& x){if (!find(x))//如果该树不存在这节点就返回false表示删除失败return false;Node* cur = _root;Node* parent = cur;while (cur){//cur往子树走的同时记录子树的父节点if (cur->_val > x)//比cur小往左子树找{parent = cur;cur = cur->_left;}else if (cur->_val < x)//比cur大往右子树找{parent = cur;cur = cur->_right;}else//已找到--分情况删除{//1.左孩子不存在//2.右孩子不存在//3.左右孩子都存在--替换删if (cur->_left == nullptr)//情况1:左孩子不存在{if (cur == _root)//如果_root刚好是要删除的节点的情况{_root = cur->_right;}//比较parent和cur的值,要分清cur的parent的那一个孩子if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;cur = nullptr;}else if (cur->_right == nullptr)//情况2.右孩子不存在{if (cur == _root)//跟上面一样_root刚好是要删除的节点的情况{_root = cur->_left;}//同样要判断cur是parent的哪一边if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;cur = nullptr;}else if (cur->_left!=nullptr && cur->_right!=nullptr)//情况3.左右孩子都存在--替换删{//这里找的是右子树的最小节点(就是右子树的最左节点)Node* min_right = cur->_right;Node* min_right_parent = cur;//记录右子树最小节点的父节点,用于后续连接while (min_right->_left){min_right_parent = min_right;min_right = min_right->_left;}swap(cur->_val, min_right->_val);//可以交换也可以覆盖原来要删除的节点//cur->_val = min_right->_val;//这个是覆盖//要删除min_right,把它的右孩子要连上if (min_right_parent->_left == min_right){min_right_parent->_left = min_right->_right;}else{min_right_parent->_right = min_right->_right;}delete min_right;min_right = nullptr;break;}else{//如果进入了else,说明都没有出现上面的情况,就是程序哪里写错了,直接断言报错assert(false);}}}return true;}void InorderTree(){_InorderTree(_root);cout << endl;}Node* findNonR(const T& x)//查找的递归版本{return findNonR(_root, x);}bool insertNonR(const T& x)//插入的递归版本{return insertNonR(_root, x);}bool eraseNonR(const T& x)//删除的递归版本{return eraseNonR(_root, x);}private:bool eraseNonR(Node*& root, const T& x){if (root == nullptr)return false;if (root->_val > x){return eraseNonR(root->_left, x);}else if (root->_val < x){return eraseNonR(root->_right, x);}else{//1.左孩子不存在//2.右孩子不存在//3.左右孩子都存在Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else if (root->_left && root->_right){Node* right_min = root->_right;Node* parent_min = root;while (right_min->_left){parent_min = right_min;right_min = right_min->_left;}swap(root->_val, right_min->_val);return eraseNonR(root->_right, x);//然后再让root->_right去递归删除交换后的x}else{//未知错误assert(false);}delete del;del = nullptr;return true;}}bool insertNonR(Node*& root,const T& x)//插入的递归版本{if (root == nullptr){root = new Node(x);return true;}if (root->_val > x){return insertNonR(root->_left, x);}else if (root->_val < x){return insertNonR(root->_right, x);}else{return false;}}Node* findNonR(Node* root,const T& x)//查找的递归版本{if (root == nullptr)return root;if (root->_val > x)return findNonR(root->_left, x);else if (root->_val < x)return findNonR(root->_right, x);elsereturn root;}void _InorderTree(Node* root){if (root == nullptr)return;_InorderTree(root->_left);cout << root->_val << " ";_InorderTree(root->_right);}private:Node* _root = nullptr;};
}
3.2 AVL树的具体代码实现
#pragma once
#include <iostream>
namespace hdm
{template<class T>struct AVLTreeNode{T _val;AVLTreeNode<T>*_left;// 该节点的左孩子AVLTreeNode<T>* _right;// 该节点的右孩子AVLTreeNode<T>* _parent;// 该节点的双亲int _bf;// 该节点的平衡因子AVLTreeNode(const T& data):_val(data), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}};template<class T>class AVLTree{public:typedef AVLTreeNode<T> Node;bool insert(const T& x){if (_root == nullptr){_root = new Node(x);return true;}Node* cur = _root;Node* parent = cur;//记录父节点用于连接新节点while (cur){//cur往子树走的同时记录子树的父节点if (cur->_val > x)//比cur小往左子树找{parent = cur;cur = cur->_left;}else if (cur->_val < x)//比cur大往右子树找{parent = cur;cur = cur->_right;}else//进入else说明cur->_val==x,表示已经存在该节点,不需要插入,返回false表示插入失败{return false;}}//程序走到这说明cur=nullptr,最后x就应该要插入在parent的下面,至于是插入左边还是右边//具体看x与parent->_val 之间值的关系cur = new Node(x);if (parent->_val > x)//如果x的值小于parent就往左边插入{parent->_left = cur;}else//如果x的值大于parent就往右边插入{parent->_right = cur;}//注意这里是三叉链结构,要把父子关系连上cur->_parent = parent;//更新平衡因子while (parent)//parent为空就结束,也就是更新到根的位置就停止{//新增在右,parent->_bf++//新增在左,parent->_bf--if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}/*判断是否更新的依据:子树的高度是否变化1.parent->_bf==0,说明parent->_bf是1或者-1,也就是说明之前是一边高一个边低这次插入填上矮的那边,parent所在子树高度不变,现在插入的节点刚好让它平衡了,就不需要向上更新了2.parent->_bf==1 或 parent->_bf==-1,说明之前parent->_bf=0,插入前是平衡的,插入之后导致一边高一边低,这个时候就要继续向上更新3.parent->_bf==2 或 parent->_bf==-2 ,说明之前parent->_bf==1 或 -1的,现在插入的节点导致严重不平衡,违反了规则,就要进行就地处理--旋转*///旋转://1.让这棵子树左右高度不超过1//2.旋转过程中进行保持它是搜索树//3.更新调整孩子节点的高度平衡因子//3.让这颗子树的高度跟插入前保持一致if (parent->_bf == 0){break;}else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转if (parent->_bf == -2 && cur->_bf == -1){//右单旋RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){//左单旋RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左旋RotateRL(parent);}else{//未知错误(比如程序写错)assert(false);}break;//旋转完了之后要break}else{//未知错误assert(false);}}return true;}Node* find(const T& x){Node* cur = _root;while (cur){if (cur->_val > x)//比cur小往左子树找{cur = cur->_left;}else if (cur->_val < x)//比cur大往右子树找{cur = cur->_right;}else//相等即返回{return cur;}}return nullptr;}void InorderTree(){InorderTree(_root);std::cout << std::endl;}bool IsBalanceTree()//检验平衡二叉树{return IsBalanceTree(_root);}private:bool IsBalanceTree(Node* root){if (root == nullptr)//空树叶是AVL树return true;// 计算root节点的平衡因子:即root左右子树的高度差int leftHeight = GetTreeHeight(root->_left);int rightHeight = GetTreeHeight(root->_right);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者// pRoot平衡因子的绝对值超过1,则一定不是AVL树if (diff != root->_bf || diff>1 || diff<-1){std::cout << root->_val << "->该节点平衡因子错误!" << "root->_bf:" << root->_bf << "实际_bf" << diff << std::endl;return false;}// root的左和右如果都是AVL树,则该树一定是AVL树return IsBalanceTree(root->_left) && IsBalanceTree(root->_right);}int GetTreeHeight(Node* root){if (root == nullptr)return 0;int left = GetTreeHeight(root->_left);int right = GetTreeHeight(root->_right);return left > right ? left + 1 : right + 1;}void InorderTree(Node* root){if (root == nullptr)return;InorderTree(root->_left);std::cout << root->_val << " ";InorderTree(root->_right);}void RotateR(Node* parent)//右单旋{/*最要注意的点就是:这个是三叉链结构,要注意处理parent节点*/Node* subL = parent->_left;Node* subLR = subL->_right;//左子树的右子树Node* pparent = parent->_parent;if (subLR)//subLR 不为空就要修改它的parentsubLR->_parent = parent;parent->_left = subLR;subL->_right = parent;parent->_parent = subL;if (pparent == nullptr)//pparent为空就表示parent为_root,就要修改整棵树的根{_root = subL;_root->_parent = nullptr;}else//不是根节点就要判断是位于pparent的那一边{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}//更新平衡因子subL->_bf = parent->_bf = 0;}void RotateL(Node* parent)//左单旋{Node* subR = parent->_right;Node* subRL = subR->_left;Node* pparent = parent->_parent;if (subRL)//subRL不为空就要连接它的parentsubRL->_parent = parent;parent->_right = subRL;subR->_left = parent;parent->_parent = subR;if (pparent == nullptr)//pparent为空就表示parent为_root,就要修改整棵树的根{_root = subR;_root->_parent = nullptr;}else//不是根节点就要判断是位于pparent的那一边{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}//更新平衡因子subR->_bf = parent->_bf = 0;}void RotateLR(Node* parent)//左右旋{Node* subL = parent->_left;Node* subLR = subL->_right;int oldBf = subLR->_bf;//记录旧的平衡因子,这样才知道是在哪插入的新节点//先左单旋,然后再右单旋RotateL(parent->_left);RotateR(parent);subLR->_bf = 0;if (oldBf == -1)//就是在原节点的左子树插入{parent->_bf = 1;subL->_bf = 0;}else if(oldBf == 1)//右子树新增{subL->_bf = -1;parent->_bf = 0;}else if (oldBf == 0)//自己就是新增的节点{subL->_bf = parent->_bf = 0;}else{//都不是上述情况只能是有些地方写错了assert(false);}}void RotateRL(Node* parent)//右左旋{Node* subR = parent->_right;Node* subRL = subR->_left;int oldBf = subRL->_bf;//记录旧的平衡因子RotateR(parent->_right);RotateL(parent);//更新平衡因子subRL->_bf = 0;if (oldBf == -1){parent->_bf = 0;subR->_bf = 1;}else if (oldBf == 1){parent->_bf = -1;subR->_bf = 0;}else if (oldBf == 0){parent->_bf = subR->_bf = 0;}else{//未知错误assert(false);}}private:Node* _root = nullptr;};void AVLTreeTest1(){int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 ,1,2,4,3,4,4,4,4,4};AVLTree<int> avl;for (auto e: a){avl.insert(e);}avl.InorderTree();cout << avl.IsBalanceTree() << endl;}
}
相关文章:

二叉树搜索树 AVL树
文章目录1. 二叉搜索树1.1 二叉搜索树概念1.2 二叉搜索树操作1.3 二叉搜索树的实现1.4 二叉搜索树的应用1.5 二叉搜索树的性能分析2. AVL 树2.1 AVL树的概念2.2 AVL树节点的定义2.3 AVL树的插入2.4 AVL树的旋转2.5 AVL树的验证2.7 AVL树的性能3. 具体代码实现区3.1 二叉搜索树的…...
nginx配置代理多个前端资源
log: 背景 两套不同的前端使用同一个后端服务,前端使用的Nginx代理的dist包 前端 vueelementui 后端 Pythonflask Nginx代理设置 1.进入Linux机器,whereis nginx 查看Nginx安装位置 2.进到Nginx配置文件下 3.vim nginx.conf 通过多个server管理…...

SuperMap iServer下载安装,启用服务,以及发布服务
supermap 是一套专注于 GIS 产品开发的全过程解决方案,主要包括桌面 GIS 、云 GIS 和 Web SDK,这里主要介绍如何使用它的云服务器 iServer 进行三维地图及数据服务的发布,iServer 里面还可进行负载均衡、集群等高级配置,有兴趣的可…...

vxe-table简单使用 vue vxe-table vue整合vxe-table vue2 vxe-table 简单使用
vxe-table简单使用 vue vxe-table vue整合vxe-table vue2 vxe-table 简单使用安装vxe-table引用使用安装vxe-table vue2稳定版本 vue3稳定版本 npm install xe-utils vxe-tablelegacy安装 vxe-table 依赖的插件 npm i xe-utils引用 我这边是全局引入,可以根据自…...

Vue项目的打包上线步骤
Vue项目的打包上线步骤一、打包之前的路由模式二、性能分析和CDN的应用2.1 性能分析2.2 webpack排除打包2.3 CDN文件配置2.4 注入CDN文件到模板一、打包之前的路由模式 两种路由模式 hash模式 : #后面是路由路径,特点是前端访问,#后面的变化不…...
都2023了,学习自动化测试还有必要么?会不会浪费我时间
最近收到不少小伙伴私信提问,其中问得比较多的就是“学习自动化测试有那么重要吗?”。 我的回答是肯定的——很重要。 相信不少同学都有诸如此类的疑问,例如:“日常工作中好像用不上自动化?”、“手工点点点好像也可…...

银行数字化转型导师坚鹏:如何有效推进银行数字化转型工作
如何有效推进银行数字化转型工作 ——以推动银行数字化转型战略落地为核心,实现知行果合一课程背景: 很多银行都在开展银行数字化转型工作,目前存在以下问题急需解决:不清楚有效推进银行数字化转型的关键性工作?不…...

【MySQL高级篇】第09章_性能分析工具的使用
第09章_性能分析工具的使用 在数据库调优中,我们的目标是 响应时间更快, 吞吐量更大 。利用宏观的监控工具和微观的日志分析可以帮我们快速找到调优的思路和方式。 1. 数据库服务器的优化步骤 当我们遇到数据库调优问题的时候,该如何思考呢࿱…...

关于xhtml和html的区别
HTML是一种基本的WEB网页设计语言,XHTML是一个基于XML的置标语言,看起来与HTML有些相象,只有一些小的但重要的区别。本文简单介绍什么是XHTML,以及与HTML相比XHTML有什么特点。 1、什么是XHTML? HTML是一种基本…...
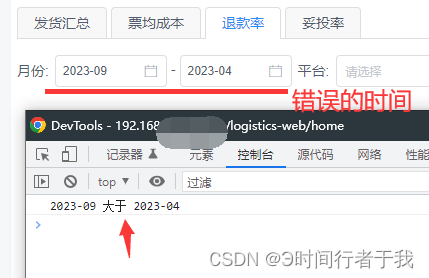
原生JavaScript比较两个日期大小,项目中通用
原生JavaScript比较两个日期大小,项目中通用,具体日期比较大小一、比较两个日期大小(月份)1.开始时间大于结束时间2.开始时间等于结束时间3.开始时间大于结束时间二、比较两个日期大小(日期)代码如下&#…...

【JAVA真的没出路了吗?】
2023年了,转行IT学习Java是不是已经听过看过很多次了。随之而来的类似学Java没出路、Java不行了、对Java感到绝望等等一系列的制造焦虑的话题也在网上层出不穷,席卷了一大片的对行业不了解的吃瓜群众或是正在学习中的人。如果是行外人真的会被这种言论轻…...
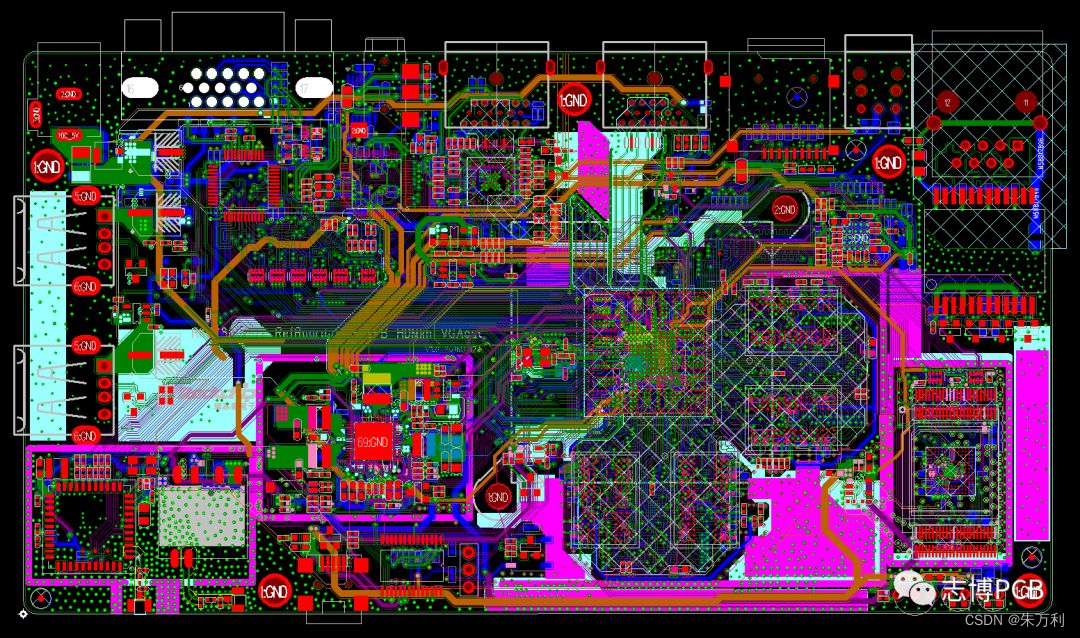
PCB模块化设计11——VGA高速PCB布局布线设计规范
目录PCB模块化设计11——VGA高速PCB布局布线设计规范1、什么是VGA?2、VGA接口管脚定义3、VGA电缆究竟是如何工作的?4、VGA参考设计原理图5、PCB设计指南1、R,G,B LAYOUT注意事项2、HSYNC,VSYNC Layout注意事项3、其他注意事项PCB模块化设计11——VGA高速…...

【Python】【进阶篇】五、Python爬虫的抓取网页
目录五、Python爬虫的抓取网页5.1 导入所需模块5.2 获取目标URL地址5.3 向目标URL发送请求5.4 保存为本地文件5.5 优化程序五、Python爬虫的抓取网页 Python 爬虫应用案例:爬取目标的网页,并将其保存到本地。 对要编写的爬虫程序进行分析,可…...
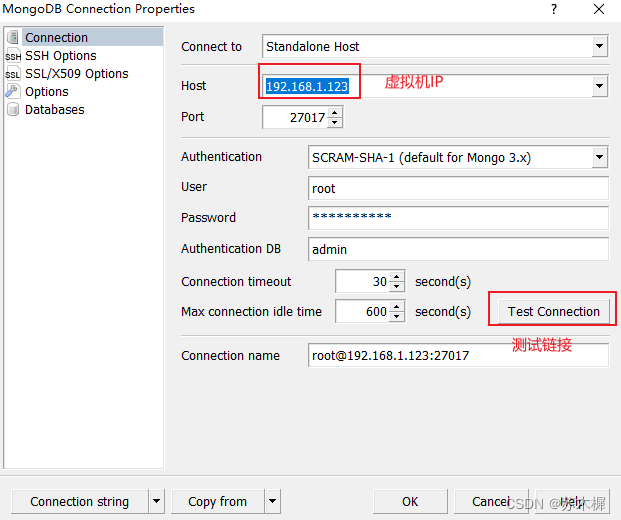
docker安装MongoBD(超详细)
一、安装docker 推荐文章:https://blog.csdn.net/Sumuxi9797926/article/details/127313307?spm1001.2014.3001.5502 二、创建主机挂载配置目录 data目录存放mongodb数据库文件,删除重启容器不会丢失 mkdir -p /docker/mongodb/data && cd …...

6轴陀螺仪姿态解算
之前看过学长姿态解算相关代码,因为要做平衡车的项目,希望陀螺仪处理数据能够达到很好的效果,大概2个星期前,看的学长代码,当时把大部分代码看懂是用来干什么的,但原理还是一窍不通,没办法&…...

提升集群吞吐量与稳定性的秘诀: Dubbo 自适应负载均衡与限流策略实现解析
作者:刘泉禄 整体介绍 本文所说的“柔性服务”主要是指 consumer 端的负载均衡和 provider 端的限流两个功能。在之前的 Dubbo 版本中,负载均衡部分更多的考虑的是公平性原则,即 consumer 端尽可能平等的从 provider 中作出选择,…...

大数据分析工具Power BI(十七):制作过程分析和原因分析图表
制作过程分析和原因分析图表 一、过程分析 过程分析主要分析业务流程中每一步骤的变化情况,用于分析业务流程指标数据变化、拆分业务流程、拆分关键业务指标等等。可以使用漏斗图、瀑布图来展示过程分析数据。 1、漏斗图 漏斗图常用来展示业务过程的线性变化,分析业务流程的转…...

公司“007”式工作的卷王测试员,被辞退了…
上周,公司传出同事小王被开除的消息,震惊了一办公室的人。要知道,小王在办公室素有卷王之称,不仅从没见他6点准点下班过,早上也都第一个到。平时的周报,也都洋洋洒洒的写了5K字之多,他的存在一度…...
)
C++ Primer第五版_第七章习题答案(1~10)
文章目录练习7.1练习7.2练习7.3练习7.4练习7.5练习7.6练习7.7练习7.8练习7.9练习7.10练习7.1 使用2.6.1节定义的Sales_data类为1.6节的交易处理程序编写一个新版本。 #include <iostream> #include <string> using std::cin; using std::cout; using std::endl; us…...

2023年全国最新保安员精选真题及答案42
百分百题库提供保安员考试试题、保安职业资格考试预测题、保安员考试真题、保安职业资格证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 421.根据《保安服务管理条例》规定,取得《保安员证》的身体条件是&#x…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
