算法笔记(十三)——BFS 解决最短路问题
文章目录
- 迷宫中离入口最近的出口
- 最小基因变化
- 单词接龙
- 为高尔夫比赛砍树
BFS 解决最短路问题
BFS(广度优先搜索) 是解决最短路径问题的一种常见算法。在这种情况下,我们通常使用BFS来查找从一个起始点到目标点的最短路径。
迷宫中离入口最近的出口
题目:迷宫中离入口最近的出口

思路
图论中边路权值为1的情况,利用层序遍历来解决是最经典的做法。
从起点开始层序遍历,在遍历的过程中记录当前遍历的层数。
C++代码
class Solution
{int dx[4] = {0, 0, 1, -1};int dy[4] = {-1, 1, 0, 0};public:int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {int m = maze.size(), n = maze[0].size();vector<vector<bool>> visited(m, vector<bool>(n, false));int ret = 0; queue<pair<int, int>> q; q.push({entrance[0], entrance[1]});visited[entrance[0]][entrance[1]] = true;while(q.size()){ret++;int sz = q.size();for(int i = 0; i < sz; i++){auto [a, b] = q.front(); q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k], y = b + dy[k];if(0 <= x && x < m && 0 <= y && y < n && maze[x][y] == '.' && !visited[x][y]){if(x == 0 || x == m - 1 || y == 0 || y == n - 1) return ret;q.push({x, y});visited[x][y] = true;}}}}return -1;}
};
最小基因变化
题目:最小基因变化

思路
转化成边路权值为1的图论问题
-
用
unordered_set<string> hash(bank.begin(), bank.end());来存储基因库,快速判断该基因是否存在于基因库 -
枚举出的每一个位置,我们先判断其是否为
合法基因(如果基因库中有并且该基因没有被访问) -
用一个
unordered_set<string> visited;用于标记是否访问过该基因序列 -
用BFS,尝试每个位置可能变异后得结果,如果变异后的基因是
合法基因,就加入队列中,并标记为已访问
C++代码
class Solution
{
public:int minMutation(string startGene, string endGene, vector<string>& bank) {unordered_set<string> hash(bank.begin(), bank.end()); // 创建一个hash方便判断该基因序列是否合法unordered_set<string> visited; // 用于标记是否访问过该基因序列string change = "ACGT"; // 可能的基因变异字符if(startGene == endGene) return 0; // 起始基因和目标基因相同,不用改变if(!hash.count(endGene)) return -1; // 目标基因不在基因库,返回-1queue<string> q;q.push(startGene); // 起始基因入队visited.insert(startGene); // 标记起始基因被访问int ret = 0;while(!q.empty()){int sz = q.size();ret++;while(sz--){string t = q.front();q.pop();for(int i = 0; i < 8; i++) // 遍历每个位置{string tmp = t;for(int j = 0; j < 4; j++) // 每个位置更改 4 次{tmp[i] = change[j];// 如果基因库中有并且该基因没有被访问,则为合法基因if(hash.count(tmp) && !visited.count(tmp)) {// 合法基因等于目标基因返回结果if(tmp == endGene)return ret;// 合法基因入队并且标记访问过了q.push(tmp);visited.insert(tmp);}}}}}return -1;}
};
单词接龙
题目:单词接龙

思路
和上一题的思路一毛一样,只不过上题每个位置变化只有四种可能,而这题每个位置的变换有二十六种可能性
C++代码
class Solution
{
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {unordered_set<string> visited; // 记录该单词是否访问过了unordered_set<string> hash(wordList.begin(), wordList.end());if (beginWord == endWord) return 1; // 起始单词和目标单词相同,不用改变if (!hash.count(endWord)) return 0; // 目标单词不在wordList,返回 0 queue<string> q;q.push(beginWord); // 起始单词入队visited.insert(beginWord); // 标记起始单词被访问int ret = 1;while(!q.empty()){ret++;int sz = q.size();while(sz--){string t = q.front();q.pop(); for(int i = 0; i < t.size(); i++) // 遍历单词的每个位置{string tmp = t;for(char ch = 'a'; ch <= 'z'; ch++) // 每个位置更改 26 次{tmp[i] = ch;// 判断是否为合法单词if(hash.count(tmp) && !visited.count(tmp)){if (tmp == endWord) return ret;q.push(tmp);visited.insert(tmp);}}}}}return 0;}
};
为高尔夫比赛砍树
题目:为高尔夫比赛砍树

思路
其实本题就是多次的迷宫问题累计求和,不停的变换起始位置
(x, y)以及终止位置(nx, ny)
- 遍历森林,将树木的位置加入
trees数组中 - 树木的高度进行排序
- 用
BFS计算起始位置(x, y)以及终止位置(nx, ny)的距离 - 累加步数,并更新起始位置
(x, y)
C++代码
class Solution
{int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int m, n;bool visited[51][51];int bfs(vector<vector<int>>& forest, int x, int y, int nx, int ny) {if (x == nx && y == ny) return 0; // 如果起始位置和目标位置相同,步数为0queue<pair<int, int>> q;memset(visited, 0, sizeof visited);q.push({x, y});visited[x][y] = true;int ret = 0;while(!q.empty()){ ret++;int sz = q.size();while(sz--){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k], y = b + dy[k];if(0 <= x && x < m && 0 <= y && y < n && forest[x][y] && !visited[x][y]){if (x == nx && y == ny) // 如果到达目标位置,返回步数return ret;q.push({x, y});visited[x][y] = true;}}}}return -1;}public:int cutOffTree(vector<vector<int>>& forest) {m = forest.size(), n = forest[0].size();// 将树的坐标存放起来vector<pair<int, int>> trees;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if (forest[i][j] > 1) trees.push_back({i, j});// 根据树木的高度进行排序sort(trees.begin(), trees.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2) {return forest[p1.first][p1.second] < forest[p2.first][p2.second];});int x = 0, y = 0; // 起始位置(0, 0)int ret = 0;// 从小到大遍历for(auto& [nx, ny] : trees){int step = bfs(forest, x, y, nx, ny);if(step == -1) return -1;ret += step;x = nx, y = ny; // 更新起始位置}return ret;}
};
相关文章:

算法笔记(十三)——BFS 解决最短路问题
文章目录 迷宫中离入口最近的出口最小基因变化单词接龙为高尔夫比赛砍树 BFS 解决最短路问题 BFS(广度优先搜索) 是解决最短路径问题的一种常见算法。在这种情况下,我们通常使用BFS来查找从一个起始点到目标点的最短路径。 迷宫中离入口最近的出口 题目:…...

Android 简单实现联系人列表+字母索引联动效果
效果如上图。 Main Ideas 左右两个列表左列表展示人员数据,含有姓氏首字母的 header item右列表是一个全由姓氏首字母组成的索引列表,点击某个item,展示一个气泡组件(它会自动延时关闭), 左列表滚动并显示与点击的索引列表item …...

自动驾驶-问题笔记-待解决
参考线的平滑方法 参考线平滑算法主要有三种: 离散点平滑;螺旋曲线平滑;多项式平滑; 参考链接:参考线平滑 对于平滑方法,一直不太理解平滑、拟合以及滤波三者的作用与区别; 规划的起点&#x…...

在掌控板中加载人教版信息科技教学指南中的educore库
掌控板中加载educore库 人教信息科技数字资源平台(https://ebook.mypep.cn/free)中的《信息科技教学指南硬件编程代码说明》文件中提到“本程序说明主要供教学参考。需要可编程主控板须支持运行MicroPython 脚本程序。希望有更多的主控板在固件中支持ed…...

关于CSS Grid布局
关于CSS Grid布局 实际效果参考 参考代码 <template><view class"baseInfo"><up-image class"cover" height"160rpx" width"120rpx" :src"bookInfo.cover"><template #error><view style"…...

初始爬虫12(反爬与反反爬)
学到这里,已经可以开始实战项目了,多去爬虫,了解熟悉反爬,然后自己总结出一套方法怎么做。 1.服务器反爬的原因 服务器反爬的原因 总结: 1.爬虫占总PV较高,浪费资源 2.资源被批量抓走,丧失竞争力…...

成像基础 -- 最大对焦清晰的物距计算
最大对焦清晰的物距计算 1. 基本概念 最大对焦清晰的物距通常与景深(Depth of Field, DOF)相关,尤其是无穷远处的物体可以被清晰对焦到的距离,称为超焦距(Hyperfocal Distance)。通过计算超焦距ÿ…...

win10服务器启动且未登录时自动启动程序
场景:公司服务器安装了几个程序,当服务器断电重启之后希望程序能自动打开,而不需要手动登录服务器打开。 因为软件是自己开发的所以安全方面这里没有考虑。 1.打开服务器管理器,点击工具,选择任务计划程序 2.在任务计…...

算法专题四: 前缀和
目录 1. 前缀和2. 二维前缀和3. 寻找数组的中心下标4. 除自身以外数组的乘积5. 和为k的子数组6. 和可被K整除的子数组7. 连续数组8. 矩阵区域和 博客主页:酷酷学!!! 感谢关注~ 1. 前缀和 算法思路: 根据题意, 创建一个前缀和数组, dp[i] dp[i -1] arr[i], 再使用前缀和数组,…...

【Linux】基础IO(文件描述符、缓冲区、重定向)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12625432.html 目录 前言 C文件IO相关操作 系统文件I/O open open函数返回值 文件描述符fd re…...

一篇文章快速学会docker容器技术
目录 一、Docker简介及部署方法 1.1Docker简介 1.1.1什么是docker 1.1.2 docker在企业中的应用场景 1.1.3 docker与虚拟化的对比 1.1.4 docker的优势 二 、部署docker 2.1 容器工作方法 2.2 部署第一个容器 2.2.1 配置软件仓库 2.2.2 安装docker-ce并启动服务 2.2.…...
【MySQL】使用 JDBC 连接数据库
文章目录 前言1. 认识 JDBC1.1 概念1.2 好处 2. 使用 JDBC2.1 安装数据驱动包2.2 把 jar 包导入到项目中2.3 代码编写2.4 测试结果 3. 代码优化4. 源码展示结语 前言 在 MySQL 系列中,我们介绍了很多内容,包括但不限于建库建表,增删查改等等…...

数据结构与算法笔记:概念与leetcode练习题
1、数组Array 时间复杂度 数组访问:O(1) 数组搜索:O(N) 数组插入:O(N) 数组删除:O(N) 特点 适合读,不适合写 数组常用操作 # 1、创建数组 a [] # 2、尾部添加元素 a.append(1) a.append(2) a.append(3) # 3、…...
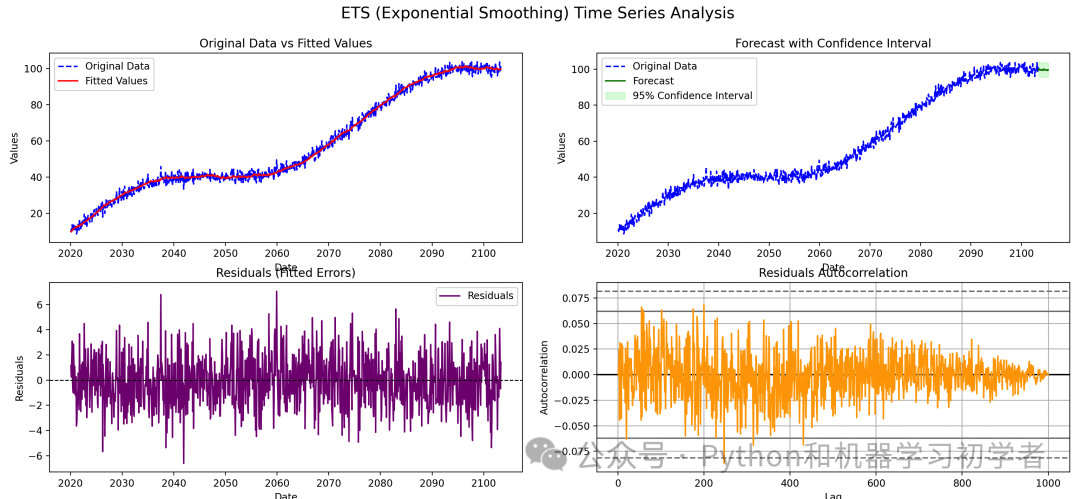
十大时间序列预测模型
目录 1. 自回归模型 原理 核心公式 推导过程: 完整案例 2. 移动平均模型 原理 核心公式 推导过程: 完整案例 3. 自回归移动平均模型 原理 核心公式 推导过程: 完整案例 4. 自回归积分移动平均模型 原理 核心公式 推导过程 完整案例 5. 季节性自回归积分…...

G2O 通过工厂函数类 OptimizationAlgorithmFactory 来生成固定搭配的优化算法
OptimizationAlgorithmFactory 类位于 optimization_algorithm_factory.h //***g2o源码 g2o/g2o/core/optimization_algorithm_factory.h ***// /*** \brief create solvers based on their short name** Factory to allocate solvers based on their short name.* The Factor…...

手机USB连接不显示内部设备,设备管理器显示“MTP”感叹号,解决方案
进入小米驱动下载界面,等小米驱动下载完成后,解压此驱动文件压缩包。 5、小米USB驱动安装方法:右击“计算机”,从弹出的右键菜单中选择“管理”项进入。 6、在打开的“计算机管理”界面中,展开“设备管理器”项&…...

SpringBootWeb快速入门!详解如何创建一个简单的SpringBoot项目?
在现代Web开发中,SpringBoot以其简化的配置和快速的开发效率而受到广大开发者的青睐。本篇文章将带领你从零开始,搭建一个基于SpringBoot的简单Web应用~ 一、前提准备 想要创建一个SpringBoot项目,需要做如下准备: idea集成开发…...

RabbitMQ 入门到精通指南
RabbitMQ 是一种开源消息代理软件,基于 AMQP(高级消息队列协议)构建,用于异步传输数据,帮助我们解耦系统、削峰流量、处理高并发。本指南将详细介绍 RabbitMQ 的架构设计、使用场景、安装步骤以及一些高级应用…...

ARM base instruction -- movz
Move wide with zero moves an optionally-shifted 16-bit immediate value to a register. 用零移动宽值将可选移位的16位即时值移动到寄存器。即把立即数移动寄存器前先把寄存器清零。 32-bit variant MOVZ <Wd>, #<imm>{, LSL #<shift>} 64-bit var…...

安装jdk安装开发环境与maven
1.下载maven 链接: https://pan.baidu.com/s/1gTmIWBFBdIQob0cqGG3E_Q 提取码: 42ck,apache-maven-3.8.4-bin.zip 2.安装java jdk yum install -y java-1.8.0-openjdk-devel 3.在/opt目录下新建目录 mkdir /opt/maven 4.将apache-maven-3.8.4-bin.zip上传到/opt/ma…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...
