Python中的Enum
Python中的Enum
Enum(枚举)在很多应用场景中都会出现,因此绝大部分编程语言都实现了Enum类型,Python也不列外,但列外的是Enum在Python3.4中才被正式支持,我们先来看看Python3中的Enum是怎么使用的。
枚举的创建方式很简单,就像创建一个类一样,只需继承Enum:
>>> from enum import Enum
>>> class Role(Enum):
... admin = 1
... manager = 2
... guest = 3
它的语法和定义class完全是一样的,但它并不是一个真正的class。这里的Role是Enum类型,里面的成员admin,manager都是它的实例对象,它们的类型是Role类型的:
>>> type(Role)
<class 'enum.EnumMeta'>
>>> type(Role.admin)
<enum 'Role'>
>>>
枚举的每一个实例对象都有自己的名字和值:
>>> Role.admin.name
'admin'
>>> Role.admin.value
1
枚举内部更像是一个OrderedDict:
Role.__members__
mappingproxy(OrderedDict([('admin', <Role.admin: 1>), ('manager', <Role.manager: 2>), ('guest', <Role.guest: 3>)]))
>>>
Python2.x:
#!/usr/bin/env python
# -*- coding: utf-8 -*-__author__ = 'liuzhijun'def enum(name, *sequential, **named):values = dict(zip(sequential, range(len(sequential))), **named)values['values'] = values.values()# NOTE: Yes, we *really* want to cast using str() here.# On Python 2 type() requires a byte string (which is str() on Python 2).# On Python 3 it does not matter, so we'll use str(), which acts as# a no-op.# return type(str(name), (), values)import collectionsaa = collections.namedtuple(str(name), values.keys())return aa(**values)JobStatus = enum('JobStatus',QUEUED='queued',FINISHED='finished',FAILED='failed',STARTED='started',DEFERRED='deferred'
)print JobStatus.QUEUED
print JobStatus.FAILED
print JobStatus.STARTED
print JobStatus._fields
print JobStatus.values
相关文章:

Python中的Enum
Python中的Enum Enum(枚举)在很多应用场景中都会出现,因此绝大部分编程语言都实现了Enum类型,Python也不列外,但列外的是Enum在Python3.4中才被正式支持,我们先来看看Python3中的Enum是怎么使用的。 枚举的…...

于BERT的中文问答系统12
主要改进点 日志配置: 确保日志文件按日期和时间生成,便于追踪不同运行的记录。 数据处理: 增加了对数据加载过程中错误的捕获和日志记录,确保程序能够跳过无效数据并继续运行。 模型训练: 增加了重新训练模型的功…...

基于SpringBoot“花开富贵”花园管理系统【附源码】
效果如下: 系统注册页面 系统首页界面 植物信息详细页面 后台登录界面 管理员主界面 植物分类管理界面 植物信息管理界面 园艺记录管理界面 研究背景 随着城市化进程的加快和人们生活质量的提升,越来越多的人开始追求与自然和谐共生的生活方式…...

MySQL连接查询:自连接
先看我的表结构 emp表 自连接也就是把一个表看作是两个作用的表就好,也就是说我把emp看作员工表,也看做领导表 自连接 基本语法 select 字段列表 FROM 表A 别名A JOIN 表A 别名B ON 条件;例子1:查询员工 及其 所属领导的名字 select a.n…...

Prometheus+Grafana备忘
Grafana安装 官网 https://grafana.com/grafana/download 官网提供了几种安装方式,我用最简单的 yum install -y https://dl.grafana.com/enterprise/release/grafana-enterprise-11.2.2-1.x86_64.rpm启动 //如果需要在系统启动时自动启动Grafana,可以…...
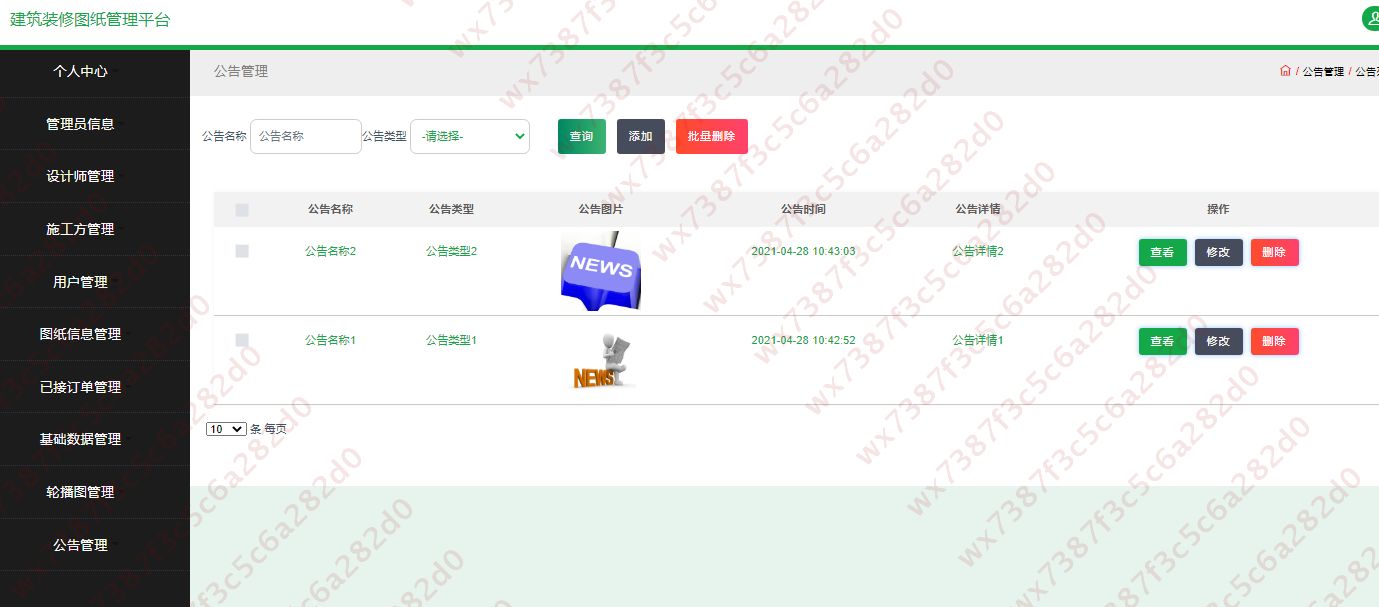
基于ssm实现的建筑装修图纸管理平台(源码+文档)
项目简介 基于ssm实现的建筑装修图纸管理平台,主要功能如下: 技术栈 后端框框:spring/springmvc/mybatis 前端框架:html/JavaScript/Css/vue/elementui 运行环境:JDK1.8/MySQL5.7/idea(可选)…...

计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-07
计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-07 目录 文章目录 计算机前沿技术-人工智能算法-大语言模型-最新研究进展-2024-10-07目录1. Evaluation of Large Language Models for Summarization Tasks in the Medical Domain: A Narrative Review摘要研究…...

Mahalanobis distance 马哈拉诺比斯距离
马哈拉诺比斯距离(Mahalanobis Distance)是一种衡量点与分布之间距离的度量,尤其适用于多维数据。与欧几里得距离不同,马哈拉诺比斯距离考虑了数据的协方差结构,因此在统计分析和异常值检测中非常有用。 定义 给定一…...

R语言绘制直方图
直方图是一种统计图表。它将数据分成若干区间,统计每个区间内数据的数量或频率,用矩形条高度表示。能直观展现数据分布特征,如集中趋势、离散程度等。在数据分析、质量控制、市场调研等领域广泛应用,可帮助人们快速了解数据整体形…...

论文阅读笔记-LogME: Practical Assessment of Pre-trained Models for Transfer Learning
前言 在NLP领域,预训练模型(准确的说应该是预训练语言模型)似乎已经成为各大任务必备的模块了,经常有看到文章称后BERT时代或后XXX时代,分析对比了许多主流模型的优缺点,这些相对而言有些停留在理论层面,可是有时候对于手上正在解决的任务,要用到预训练语言模型时,面…...

求二叉树的带权路径长度
二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和。给定一棵二叉树T,采用二叉链表存储。结点结构为: 其中叶结点的weight域保存该结点的非负权值。设root为指向T的根结点的指针,请设计求T的WPL的算法…...
)
Hive数仓操作(十五)
Hive 开窗函数 Hive窗口函数是一种特殊的函数,允许用户在查询中对一组行进行计算,而不仅仅是单独的行。窗口函数可以在 SQL 查询中进行聚合、排名、累积计算等。这使得窗口函数在数据分析和报告生成中非常有用。 窗口函数的基本组成部分 函数类型&…...

No.12 笔记 | 网络基础:ARP DNS TCP/IP与OSI模型
一、计算机网络:安全的基石 1. 网络的本质:数字世界的神经系统 定义:计算机的互联互通,实现资源共享和信息交换组成要素:发送者、接收者、介质、数据、协议(五大要素) 2. 网络架构࿱…...

OpenHarmony(鸿蒙南向开发)——轻量系统STM32F407芯片移植案例
往期知识点记录: 鸿蒙(HarmonyOS)应用层开发(北向)知识点汇总 鸿蒙(OpenHarmony)南向开发保姆级知识点汇总~ 持续更新中…… 介绍基于STM32F407IGT6芯片在拓维信息 Niobe407 开发板上移植OpenH…...

简单易懂的springboot整合Camunda 7工作流入门教程
简单易懂的Spring Boot整合Camunda7入门教程 因为关于Spring Boot结合Camunda7的教程在网上比较少,而且很多都写得有点乱,很多概念写得太散乱,讲解不清晰,导致看不懂,本人通过研究学习之后就写出了这篇教学文档。 介…...
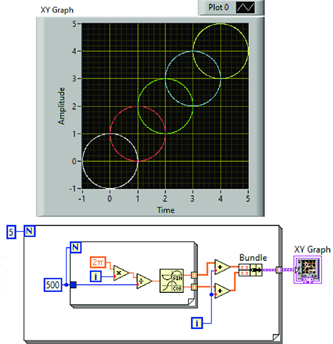
LabVIEW提高开发效率技巧----点阵图(XY Graph)
在LabVIEW开发中,点阵图(XY Graph) 是一种强大的工具,尤其适用于需要实时展示大量数据的场景。通过使用点阵图,开发人员能够将实时数据可视化,帮助用户更直观地分析数据变化。 1. 点阵图的优势 点阵图&…...

C++-匿名空间
匿名命名空间(anonymous namespace)是 C 中的一种特性,用于将符号(如变量、函数或类)限制在定义它们的源文件的作用域内。这意味着在该源文件外部,这些符号不可见,从而避免了命名冲突。 1. 定义…...

jdk的安装和环境变量配置
1.将从官网下载好的jdk放在自己想要放的位置,这里的位置是:E:\develop 2.新建一个文件夹用来放安装的jdk,将jdk安装的此目录,这里的位置是:E:\develop\jdk17 3.jdk安装好之后,点击jdk17目录,点…...

继承、Lambda、Objective-C和Swift
继承 东风系列导弹是镇国神器。东风41不是突然就造出来的,之前有很多种东风xx导弹,每种导弹都有自己的独特之处,相同之处都具备导弹基本特点。很多工厂有量产磨具的生产线,盖房子就图纸,建筑设计建设都有参考ÿ…...

设置服务器走本地代理
勾选: 然后: git clone https://github.com/rofl0r/proxychains-ng.git./configure --prefix/home/wangguisen/usr --sysconfdir/home/wangguisen/etcmakemake install# 在最后配置成本地代理地址 vim /home/wangguisen/etc/proxychains.confsocks4 17…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
