2022CCPC绵阳站VP题解报告(CGHMAE六题)
文章目录
- 2022CCPC绵阳站VP题解报告
- 前言
- [Problem - C ](https://codeforces.com/gym/104065/problem/C) (签到思维)
- [H (codeforces.com)](https://codeforces.com/gym/104065/problem/H) (签到构造)
- [Problem - G ](https://codeforces.com/gym/104065/problem/G) (签到思维)
- [Problem - M](https://codeforces.com/gym/104065/problem/M) (栈)
- [Problem - A ](https://codeforces.com/gym/104065/problem/A)(记忆化搜索)
- [Problem - E ](https://codeforces.com/gym/104065/problem/E) (图论上的DP,根号分治优化)
2022CCPC绵阳站VP题解报告
前言
- 队伍VP赛时 CGHME 五题,赛后A题。
- 赛时个人出了CHE,赛后补3题GMA。
- 题解按赛场过题人数排序。
Problem - C (签到思维)
注意到每次每个点的蝴蝶所在点的深度都会减少1,所以只需要在 1 号节点的所有孩子节点操作即可,答案就是1号节点的所有孩子的高度之和。
ac代码参考:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 5, M = 2e5 + 5;int n, tot;
int head[N], ver[M], nxt[M], dep[N];inline void add(int x, int y){ver[++tot] = y; nxt[tot] = head[x]; head[x] = tot;
}void dfs(int x, int fa = 0){dep[x] = 1;for(int i = head[x]; i; i = nxt[i]){int y = ver[i];if(y == fa) continue;dfs(y, x);dep[x] = max(dep[x], dep[y] + 1);}
}void solve(){tot = 1;cin >> n;for(int i = 1; i < n; i++){int x, y;cin >> x >> y;add(x, y);add(y, x);}dfs(1);int ans = 0;for(int i = head[1]; i; i = nxt[i]){ans += dep[ver[i]];}cout << ans << '\n';
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);solve();return 0;
}
H (codeforces.com) (签到构造)
注意到 k ≤ 100 k \le 100 k≤100,所以我们完全可以铺开来,只考虑单元每轮死亡到少个不必考虑复活的事,所以延对角线输出 2 k 2k 2k 个点即可。
ac代码参考:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;void solve(){int k; cin >> k;cout << k * 2 << '\n';for(int i = 1; i <= 2 * k; i++){cout << i << ' ' << i << '\n';}
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);solve();return 0;
}
Problem - G (签到思维)
考虑相邻的两个数,其中较小的数一定无法存活至下一轮。因此每 一轮至少有一半(向下取整)的数字被删除,暴力模拟即可。
ac代码参考:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;void solve(){int n,x;cin>>n;vector<int> a;for(int i=1;i<=n;i++) cin>>x,a.push_back(x);vector<int> b;int ans=0;while(a.size()!=1){b.clear();for(int i=0;i<a.size();i++){if(i==0){if(a[i]>a[i+1]) b.push_back(a[i]);}else if(i==a.size()-1){if(a[i]>a[i-1]) b.push_back(a[i]);}else{if(a[i]>a[i+1]&&a[i]>a[i-1]) b.push_back(a[i]);}}a=b;ans++;}cout<<ans<<'\n';
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);solve();return 0;
}
Problem - M (栈)
注意到如果一段相同的字符 X X X 的左右两端点相邻 Y Y Y, 且 Y Y Y 能赢 X X X,则将这一段 X X X 全部换成 Y Y Y 不会影响答案。同理,如果 X X X 块位于序列的一端,且另一边与 Y Y Y 相邻。则也可以将这一段 X X X 全部换成 Y Y Y 不会影响答案。那么,我们就可以用一个栈来不断维护并更新 R P S RPS RPS 序列,时间复杂度 O ( ∣ s ∣ ) O(|s|) O(∣s∣)。
ac代码参考:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;void solve(){string s;cin >> s;stack<char> st;st.push(s[0]);for(int i = 1; i < s.length(); i++){while(!st.empty()){char pre = st.top();if(s[i] == 'R')if(pre == 'P') break;else if(s[i] == 'P')if(pre == 'S') break;else if(s[i] == 'S')if(pre == 'R') break;st.pop();}st.push(s[i]);}while(st.size() > 1) st.pop();cout<< st.top() <<'\n';
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int T;cin >> T;while(T--) solve();return 0;
}
Problem - A (记忆化搜索)
注意到选取或禁用英雄时,一定会选择己方和对方剩余英雄中价值最大的。当某方选到 k k k 个英雄后,它不会再做“选取英雄”操作,而是 尽可能地去做“禁用英雄”操作。所以双方轮流操作时能到达的”状态数”只有 O ( n k 2 ) O(nk^2 ) O(nk2)个。
我们用 d p ( x , i , j ) dp(x, i, j) dp(x,i,j) 表示当前双方总共操作 x x x 轮,分别已经选取了 i , j i, j i,j 个英雄时的答案。然后记忆化搜索即可。
ac代码参考:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 2e5 + 5;int n, m, a[N], b[N], f[N][11][11];
bool vis[N][11][11];int dfs (int x, int ca, int cb) {if (x >= 2 * n) return 0;if (vis[x][ca][cb]) return f[x][ca][cb];vis[x][ca][cb] = true;int aa = x / 2 - cb + ca + 1, bb = (x + 1) / 2 - ca + cb + 1, &t = f[x][ca][cb];t = dfs (x + 1, ca, cb); //不选if (x % 2 == 0) { //Aif (aa <= n && ca < m) t = max (t, dfs (x + 1, ca + 1, cb) + a[aa]);} else { //Bif (bb <= n && cb < m) t = min (t, dfs (x + 1, ca, cb + 1) - b[bb]);}return t;
}void solve(){cin >> n >> m;for (int i = 1; i <= n; i++) cin >> a[i];for (int i = 1; i <= n; i++) cin >> b[i];sort (a + 1, a + n + 1, greater<int>());sort (b + 1, b + n + 1, greater<int>());cout << dfs (0, 0, 0) << '\n';
}int main () {ios::sync_with_stdio(false);cin.tie(nullptr); cout.tie(nullptr);solve();
}
Problem - E (图论上的DP,根号分治优化)
对于这个问题,其实我们不必管 a i a_i ai,我们只要求出点权为 1 1 1 转移的最小代价最后乘以权值即可,这么转换后我们不难想到一个暴力的 D P DP DP 做法,令 f ( i , j ) f(i,j) f(i,j) 表示第 j j j 号点,在第 i i i 天后的所有操作中所需的最小代价。那么转移就明显了,第 i i i 天需要转移 b i b_i bi,那么 f ( i , b i ) = min ( b i , y ) ∈ e d g e { w ( b i , y ) + f ( i + 1 , y ) } f(i,b_i) = \min_{(b_i,y)\in edge}\{w(b_i,y) + f(i + 1, y)\} f(i,bi)=min(bi,y)∈edge{w(bi,y)+f(i+1,y)} 其中 w ( x , y ) w(x,y) w(x,y) 为边权。
但是,像上述 D P DP DP 解法,时间和空间上都会超出限制,我们考虑怎么优化。由于每一天我们只会更新某一个 j j j 的值,所以我们可以直接省略 f f f 的第一维。此外,状态的转移是图的邻域问题,我们可以考虑一个常用的套路:根号分治。我们选取一个阈值 B B B,对所有的点按度数的大小分为两类:
- 对于度数小于 B B B 的点 j j j,我们只需要枚举来更新 f ( j ) f(j) f(j) 的的值。
- 对于度数大于 B B B 的点 j j j,我们考虑维护一个 m u l t i s e t multiset multiset,对所有连向 j j j 的边 ( x , j ) (x,j) (x,j),将 f ( x ) + w ( x , j ) f(x) + w(x,j) f(x)+w(x,j) 放入集合。每次我们只需要从集合中取出最小值更新 f ( j ) f(j) f(j),再枚举所有连接的度数大于 B B B 的点,更新多重集即可。
对于度数小于 B B B 的点,我们转移的复杂度是 O ( B ) O(B) O(B) 的,对于度数大于 B B B 的点最多有 2 m B \frac{2m}{B} B2m 个,每次转移的复杂度是 O ( m B log n ) O(\frac{m}{B}\log{n}) O(Bmlogn) 的。当 B = 2 m log n B = \sqrt{2m\log n} B=2mlogn 时,总的复杂度为 O ( q m log n ) O(q\sqrt{m\log n}) O(qmlogn)。
ac代码参考:
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 5, M = 2e5 + 5;
const int mod = 998244353;int n, m, q, tot, tb;
ll a[N], b[N], f[N], deg[N], edge[M], eb[M];
int head[N], ver[M], nxt[M];
int hb[N], vb[M], nb[M];
multiset<ll> se[N];inline void add(int x, int y, ll z){ver[++tot] = y; edge[tot] = z;nxt[tot] = head[x]; head[x] = tot;
}
inline void addb(int x, int y, ll z){vb[++tb] = y; eb[tb] = z;nb[tb] = hb[x]; hb[x] = tb;
}void solve(){tot = tb = 1;cin >> n >> m >> q;int SQ = sqrt(2ll * m * log2(n));for(int i = 1; i <= n; i ++) cin >> a[i];for(int i = 1; i <= m; i++){int x, y, z;cin >> x >> y >> z;add(x, y, z); add(y, x, z);deg[x] ++; deg[y] ++;}for(int x = 1; x <= n; x++) if(deg[x] > SQ)for(int i = head[x]; i; i = nxt[i]){int y = ver[i], z = edge[i];se[x].insert(z + f[y]);if(deg[y] > SQ) addb(y, x, z);}for(int i = 1; i <= q; i ++) cin >> b[i];for(int j = q; j; j--){int x = b[j];if(deg[x] <= SQ){ll cost = 1e18;for(int i = head[x]; i; i = nxt[i])cost = min(cost, edge[i] + f[ver[i]]);for(int i = head[x]; i; i = nxt[i]){int y = ver[i], z = edge[i];if(deg[ver[i]] > SQ){se[y].erase(se[y].find(z + f[x]));se[y].insert(cost + z);}}f[x] = cost;}else {for(int i = hb[x]; i; i = nb[i])se[vb[i]].erase(se[vb[i]].find(f[x] + eb[i]));f[x] = *se[x].begin();for(int i = hb[x]; i; i = nb[i])se[vb[i]].insert(f[x] + eb[i]);}}ll ans = 0;for(int i = 1; i <= n; i++){ans = (ans + f[i] * a[i]) % mod;}cout << ans << '\n';
}int main()
{ios::sync_with_stdio(false);cin.tie(nullptr); cout.tie(nullptr);solve();return 0;
}
相关文章:
)
2022CCPC绵阳站VP题解报告(CGHMAE六题)
文章目录 2022CCPC绵阳站VP题解报告前言[Problem - C ](https://codeforces.com/gym/104065/problem/C) (签到思维)[H (codeforces.com)](https://codeforces.com/gym/104065/problem/H) (签到构造)[Problem - G ](https://codefo…...

代码随想录day23:贪心part1
455. 分发饼干 class Solution {public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int res 0;int index s.length - 1;for(int i g.length - 1; i > 0; i--){if(index > 0 && s[index] > g[i]){res;index--;}}return r…...

通过网页设置参数,submit还是json
在通过网页设置参数并发送到服务器时,选择使用submit(通常是通过HTML表单的提交)还是直接发送JSON数据(通常是通过AJAX请求,如使用fetch API)取决于几个因素,包括你的服务器端如何处理这些请求、…...

C语言 | Leetcode C语言题解之第463题岛屿的周长
题目: 题解: const int dx[4] {0, 1, 0, -1}; const int dy[4] {1, 0, -1, 0};int dfs(int x, int y, int** grid, int n, int m) {if (x < 0 || x > n || y < 0 || y > m || grid[x][y] 0) {return 1;}if (grid[x][y] 2) {return 0;}g…...

逼近理论及应用精解【12】
文章目录 卷积卷积层与滤波层定义数学原理与公式定理架构例子例题 卷积层和滤波层概念的详细解释卷积层滤波层 滤波层和卷积层在卷积神经网络(CNN)中区别滤波层卷积层总结卷积层的数学原理滤波层的数学原理 参考文献 卷积 卷积层与滤波层 定义 卷积层…...

LIN总线学习大全(基于CANoe和CAPL)
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...
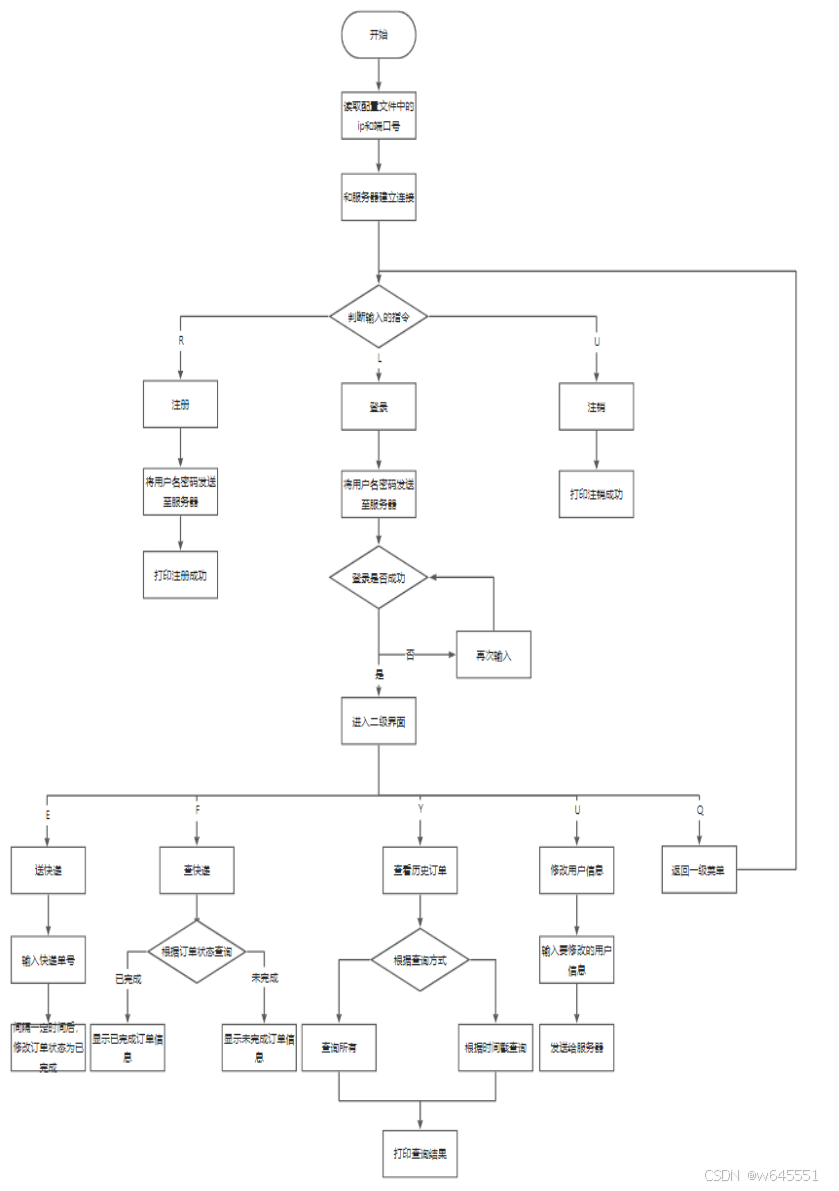
国庆作业
day1 1.开发环境 Linux系统GCCFDBmakefilesqlite3 2.功能描述 项目功能: 服务器:处理客户端的请求,并将数据存入数据库中,客户端请求的数据从数据库进行获取,服务器转发给客户端。 用户客户端:实现账号的注册、登…...
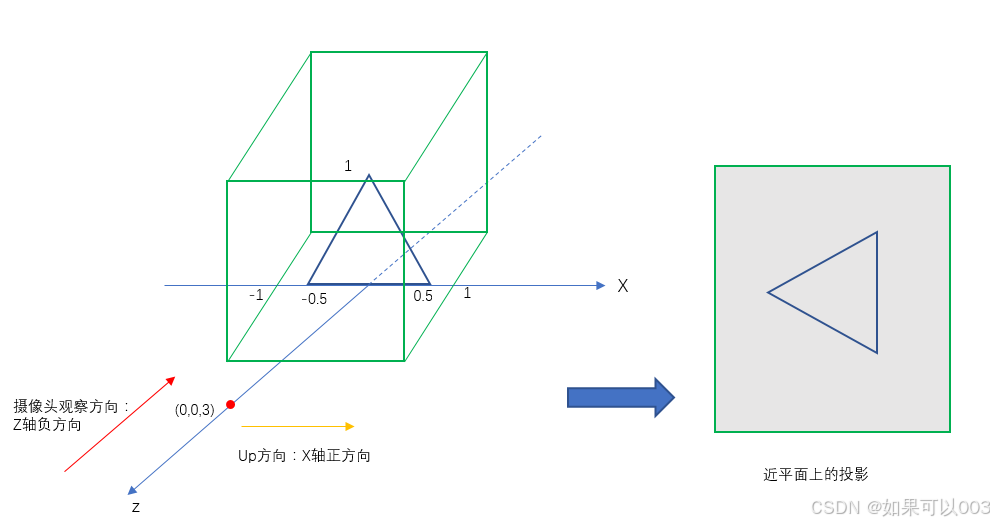
Android OpenGLES2.0开发(四):矩阵变换和相机投影
事物的本质是事物本身所固有的、深藏于现象背后并决定或支配现象的方面。 还记得我们上一篇绘制的三角形吗,我们确实能够顺利用OpenGL ES绘制出图形了,这是一个好的开始,但这还远远不够。我们定义的坐标是正三角形,但是绘制出…...
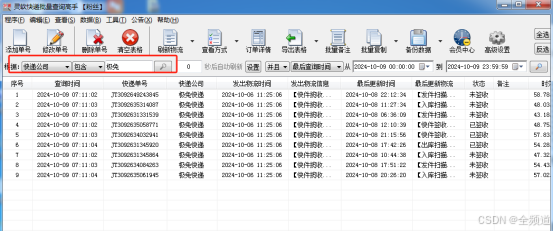
快递查询软件:实现单号识别与批量物流查询的高效工具
随着网络购物的普及,快递物流行业迎来了前所未有的发展机遇,同时也面临着巨大的挑战。跟踪物流信息成为一个难题,因此,快递查询软件的核心功能之一便是单号识别。传统的快递单号输入方式繁琐且易出错在此背景下,快递查…...
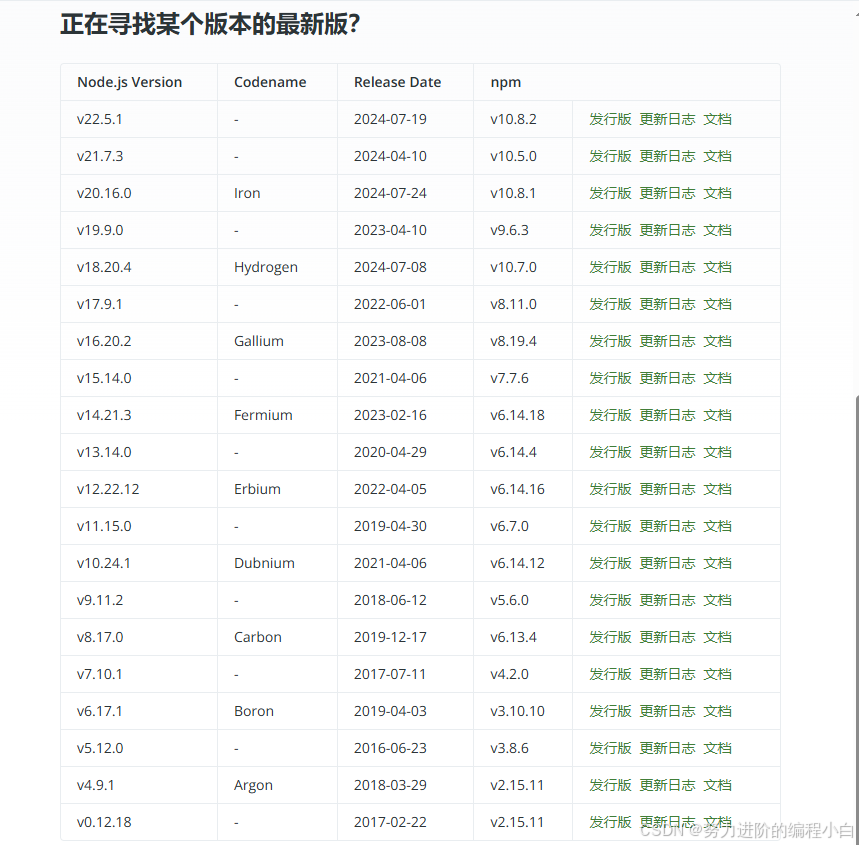
nodejs与npm版本对应表
Node.js — Node.js 版本 (nodejs.org)...

Spring Boot 项目中如何使用异步任务
前置知识: 同步任务: 同步任务是在单线程中按顺序执行,每次只有一个任务在执行,不会引发线程安全和数据一致性等并发问题 同步任务需要等待任务执行完成后才能执行下一个任务,无法同时处理多个任务,响应慢…...

Scrum实战中遇到的问题与解决方法
在当今快速变化的技术环境中,IT企业面临着持续的市场压力和竞争,传统的瀑布式开发模式已经难以满足现代企业的需要。瀑布模型过于僵化,缺乏灵活性,导致项目经常延期,成本增加,最终可能无法达到预期效果。为…...
全面介绍 Windows 录屏工具:开启录制新篇章
高质量的录屏工具是我们录屏的得力助手。但是日常因为侧重点的不同,比如有的喜欢录制游戏画面、有的需要录制教学视频、演示操作也需要录屏工具。这次我们就来探讨一下windows录屏工具有哪些吧。 1.福晰录屏大师 链接:www.foxitsoftware.cn/REC/ 从这…...

Maven 和 NetBeans:集成与使用
Maven 和 NetBeans:集成与使用 Maven 和 NetBeans 是两款强大的工具,常用于Java开发。Maven是一个项目管理工具,它能够帮助管理项目的构建、报告和文档。NetBeans是一个集成开发环境(IDE),它为Java开发提供了丰富的功能和友好的用户界面。将Maven集成到NetBeans中,可以…...

【系统架构设计师】目录提纲
一、绪论(TODO) 二、计算机与网络基础知识(TODO) 三、信息系统基础知识(TODO) 四、系统开发基础知识(TODO) 五、软件架构设计(TODO) 六、UML建模与架构文…...

【微服务】—SpringBoot入门
⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记仓库👉https://github.com/A-BigTree/tree-learning-notes 个人主页👉https://www.abigtree.top ⭐⭐⭐⭐⭐⭐ 文章目录 1 SpringBoot快速入门1.1 SpringBoot简介1.1.1 简介1.1.2…...

Linux: debug: perf: report: --sort
文章目录 简介实例简介 接上回:https://mzhan017.blog.csdn.net/article/details/142689870。 这里介绍perf的这个参数,还是非常的有用,尤其是分析对整个系统做perf record的数据,而不是单个进程做perf record。-s, --sort= : Sort histogram entries by given key(s) - …...

like 模糊查询的底层算法
like 模糊查询的底层算法 全文搜索算法、模糊查询、n-gram分隔算法功能介绍 百度搜索,文心一言给出的结果: SQL模糊查询底层通常使用全文搜索算法,如LIKE操作符和全文索引通常使用的n-gram分割算法。 n-gram是一种将文本分割成固定大小的词…...
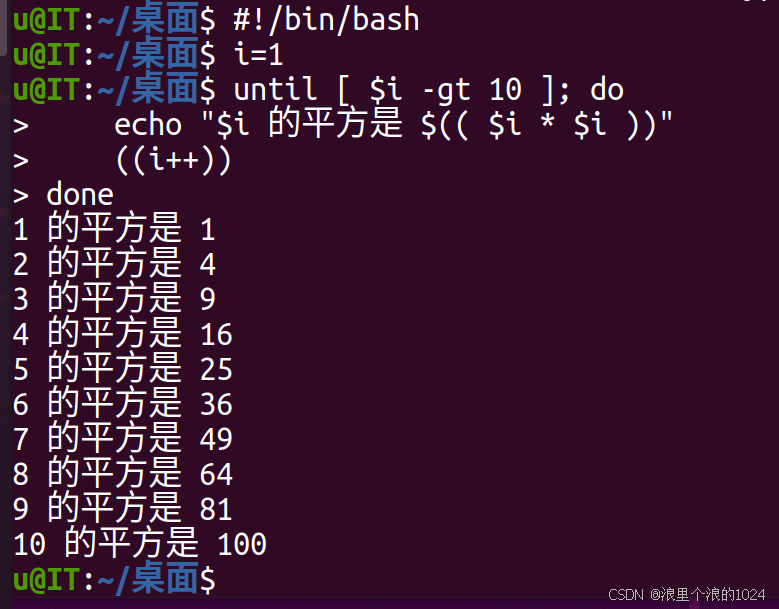
【Linux实践】实验九:Shell流程控制语句
文章目录 实验九:Shell流程控制语句实验目的:实验内容:操作步骤:1. 复制*.c文件并排序2. 计算1-10的平方 实验九:Shell流程控制语句 实验目的: 掌握条件判断语句,如if语句、case语句。掌握循环…...
YOLOv8实战TT100K中国交通标志检测【数据集+YOLOv8模型+源码+PyQt5界面】
YOLOv8实战TT100k交通标志识别 文章目录 研究背景资源获取1.前言1.1 YOLO 系列:中国交通标志检测领域的璀璨明星1.2 Transformer与注意力机制:为中国交通标志检测注入新活力1.3 中国交通标志检测技术:迎接挑战,砥砺前行1.4 YOLOv8…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...
