ML 系列：【13 】— Logistic 回归（第 2 部分）

一、说明

​
在这篇文章中，我们将深入研究 squashing 方法，这是有符号距离方法（第 12节）的一种很有前途的替代方案。squashing 方法通过提供增强的对异常值的弹性来解决有符号距离方法的缺点，从而提高 Logistic 回归模型的整体性能和准确性。

在整个讨论中，我们将对 shushing 方法进行概述，详细介绍其基本原理并说明其相对于有符号距离方法的优势。通过了解这种替代方法的复杂性，我们的目标是为从业者提供一个有价值的工具，以有效处理异常值并增强 Logistic 回归模型的稳健性。

二、挤压方法

这种方法不是使用简单的有符号距离，而是如果提到的距离很小，我们就按原样使用它，如果有符号距离是一个很大的数字，我们就减少该值。所以，我们需要一个函数，当输入值较小时线性增加，当输入值较大时，它减少输出值，这个函数将输入从负无穷大映射到 0 到 1 之间的无穷大，对于这种行为，它被称为“挤压”。其中一个函数是 sigmoid 函数。Sigmoid 是一个实数、有界且可微分的函数，可以针对所有实数值进行定义，并且具有正导数。从图形上看，此函数类似于英语中的字母“S”和希腊语中的 sigma “Ϭ”，在某些来源中，它也称为 sigma 函数。sigmoid 函数也称为 logistic 函数，该函数是这样的，如果 x 的值趋向于正无穷大，则预测值或 y 是接近 1 的数字，如果趋向于负无穷大，则预测值或 y 是接近零的数字。可以是 sigmoid 函数显示在表达式 1 中。

sigmoid 函数的表达式 1：

图 1 显示了 sigmoid 函数

​

图 1 显示了 sigmoid 函数。
在这个函数中，如果输入数字为零，则输出数字为 0.5，可以假设如果输出大于 0.5，则结果为 1 类 （y_i = +1），如果小于 0.5，则将其归类为负类 （y_i = -1）。

我们在上一节（第 12 天）之前想要最大化的优化问题：

应该更改此表达式，以便我们通过 sigmoid 函数 “Ϭ” 传递有符号区间值，并显示使用 sigmoid 函数的 Logistic 回归算法：

Logistic 回归的目标是最大化上述表达式。

三、Logistic 回归中的损失函数

双类分类中使用的函数之一是 “Binary Cross Entropy” 函数。此函数将每个预测概率与相应类或标签的实际输出（可以是 0 或 1）进行比较，然后计算一个分数，该分数根据与预期值的距离对概率进行惩罚。这意味着它与每个类的 label 值的接近或距离。

下面的方程式以分段函数的形式显示了此函数：

此外，上述函数也可以使用以下公式编写，如下面的等式所示：

“二进制交叉熵”函数的方程如下：

在上面的等式中，p_i 指的是算法的概率输出值，我们通常用 y-hat 表示，但在这个例子中，需要强调的是，这个值是带有 p_i 的概率输出，它是从第一个字母“Probability”派生出来的，y_i也指每个类的标签或实际输出，当该值等于数字 1 （y_i = 1） 时，只有执行第一个短语，第二个短语变为零，同样，当此值等于零 （y_i = 0） 时，仅执行第二个短语，第一个短语的值变为零，n 引用数据数。从上面的语句中可以看出，算法的输出值是通过对数函数传递的，因此，它在某些来源中也被称为 “Log Loss”。

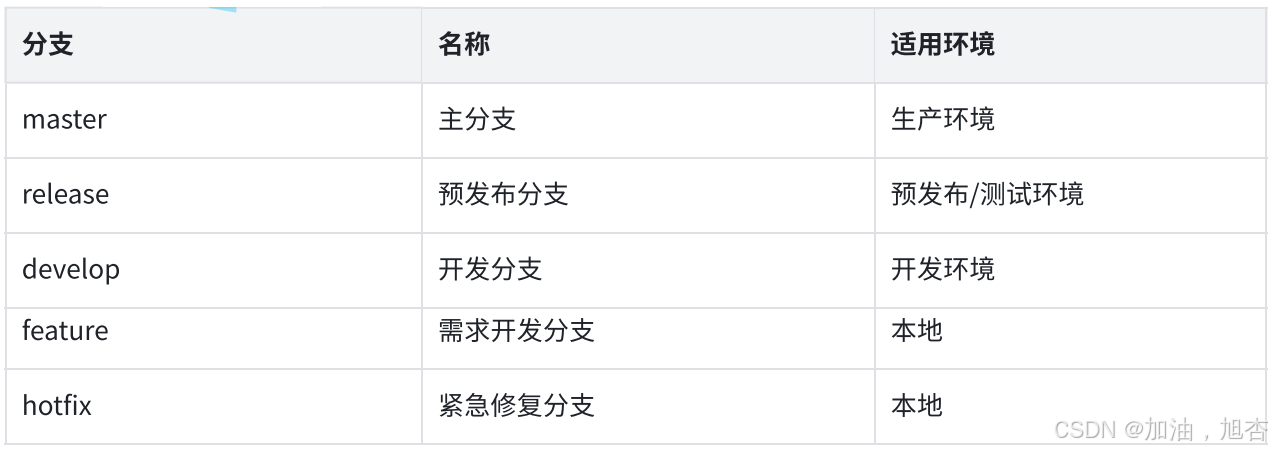
我们用表 1 中的一个例子来展示这个函数的性能。

​

表 1.如何计算 “Binary Cross Entropy” 损失函数的示例

在第一个数据 （x_1） 中，实际输出值或标签为 1，算法的预测值为 0.95 且接近 1，此数据的误差值为 0.022。现在，如果我们关注第二行，这个数据的实际输出值是 1，但是预测值是 0.6，不出所料，这个数据的生产误差比第一行高，因为算法的发生率较小，或者换句话说，它与第一行相比有一个远的鼻子， 同样，如果我们看属于零类的第三和第四个数据，第三个数据的误差值低于第四个数据的误差，因为 0.15 的预测比第四个数据中预测的数字 0.55 更接近零类。

注意：让我们看看为什么我们应该在损失函数中使用负对数函数 （-log （p_i）），原因是算法产生的可能输出 （p_i） 介于 0 和 1 之间，并且我们知道 0 和 1 之间的数字的对数是负数， 因此，使用负系数 1 来避免产生负误差。

图 4 显示了从 0 到 5 的输入的对数函数的输出。

​

图 4.区间 0 到 5 的对数函数

四、后记

我分两部分解释了逻辑回归的理论，在下一部分机器学习系列： 逻辑回归（第 3 部分 — 实施）中，我想深入研究使用 Python 代码进行逻辑回归的简单实现。