动态规划总结
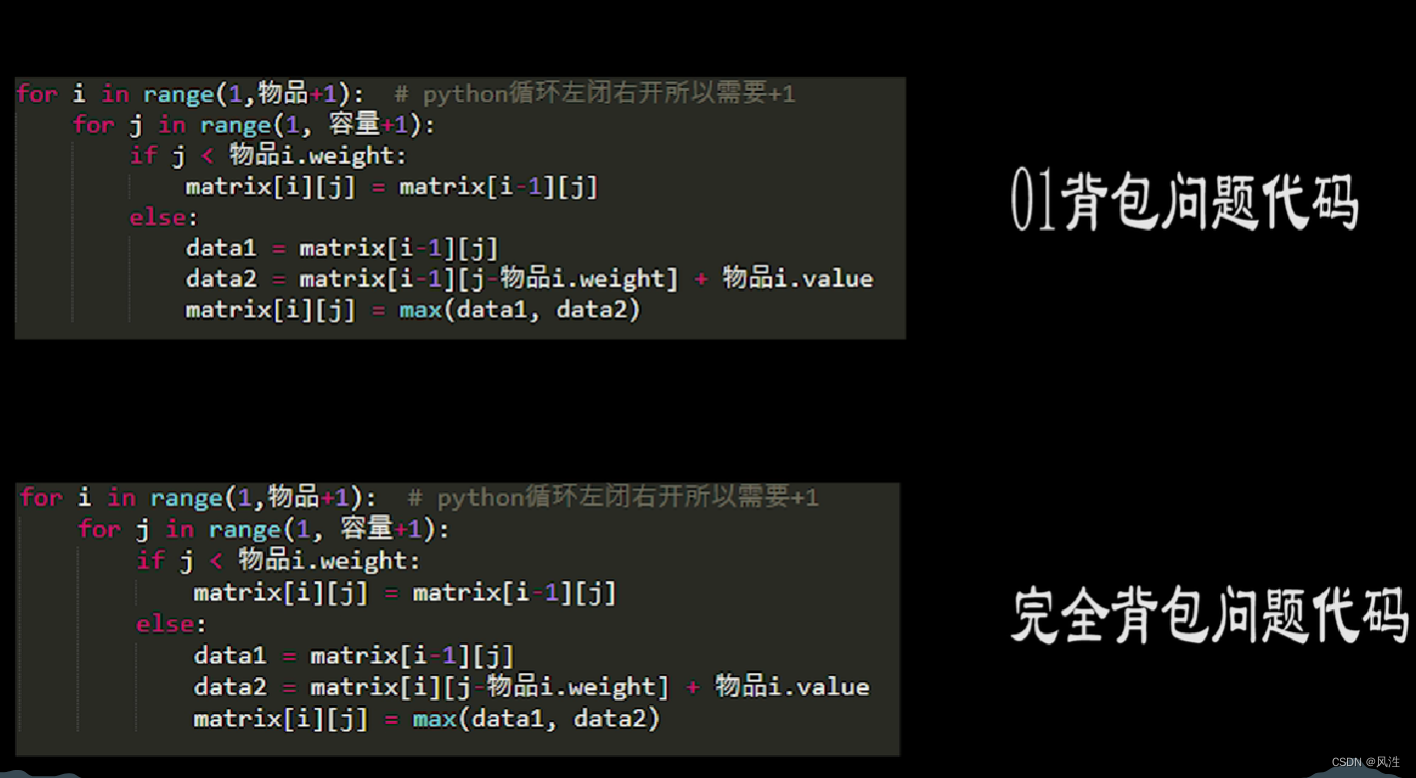
1,01背包dp(每件物品最多选一次):
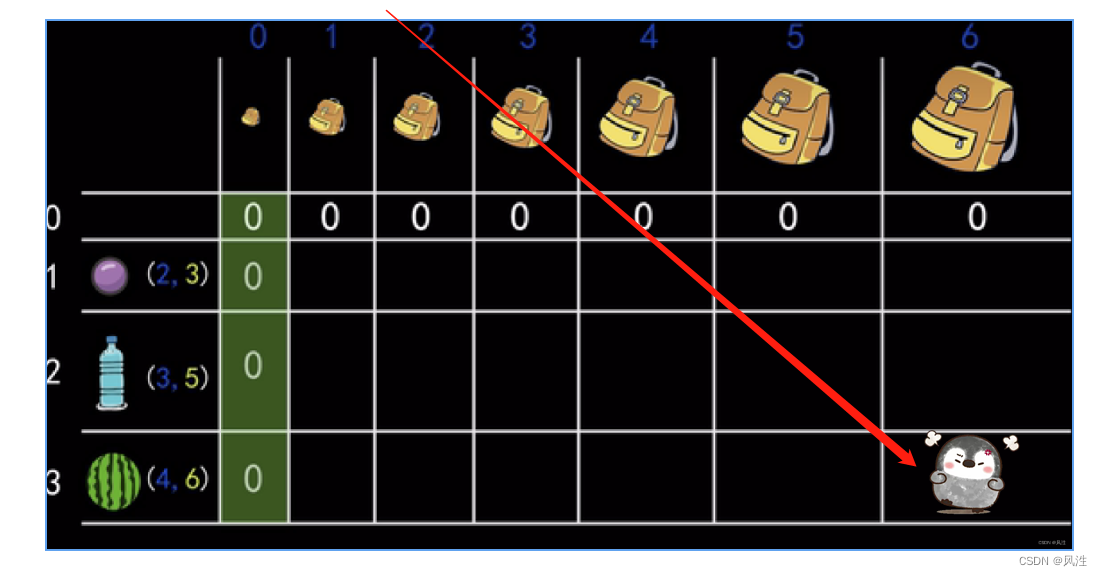
因为背包为0 的时候,什么都装不了,所以为零 ,就是他们的最优解。
最后一个单元格为最后的答案。
01背包模板
public class Knapsack {public static int knapsack(int[] weights, int[] values, int capacity) {int n = weights.length;int[][] dp = new int[n + 1][capacity + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= capacity; j++) {if (weights[i - 1] > j) {dp[i][j] = dp[i - 1][j];} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1]);}}}return dp[n][capacity];}public static void main(String[] args) {int[] weights = {10, 20, 30};int[] values = {60, 100, 120};int capacity = 50;System.out.println("The maximum value that can be put in a knapsack of capacity " + capacity + " is: " + knapsack(weights, values, capacity));}
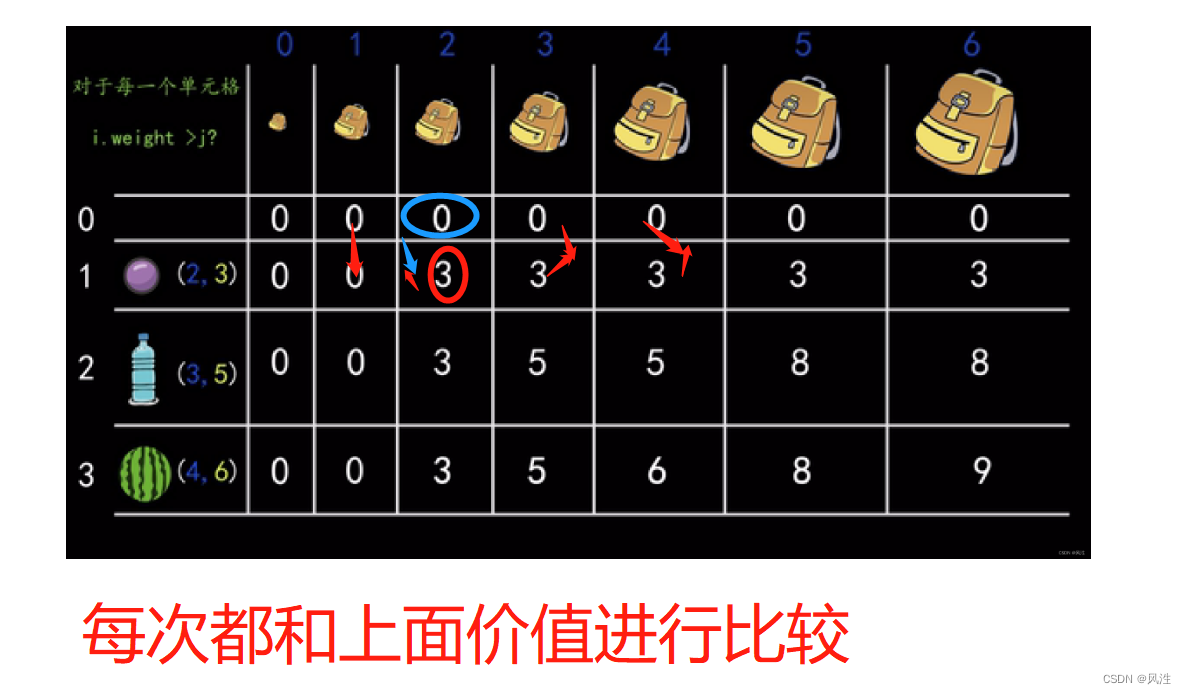
}当j比现在取的物品重量小的时候:
继承上一个的值:——>dp[i][j] = dp[i - 1][j](上一个物品价值);
当j>=w[i]:有两种情况,一种是拿,一种是不拿:
核心: dp[i][j] = Math.max(dp[i - 1][j](不拿), dp[i - 1][j - weights[i - 1]] + values[i - 1](拿));
难点: 这里表示,如果容量为3 ,之前存放的一直是重量2 的价值 , 那么遇到一个重量为3 的价值更高的, 那么我们肯定选择更高的 那么要就要更新重量为2 的价值为重量3的价值 ,dp[i - 1][j - weights[i - 1]] + values[i - 1](价值);
在以上代码中,我们定义了一个函数 knapsack 接受三个参数:weights表示物品的重量数组,values表示物品的价值数组,capacity表示背包的容量。我们首先初始化一个大小为(n+1)x(capacity+1)的二维数组dp。其中,dp[i][j]表示前i个物品放入容量为j的背包中所能获得的最大价值。
然后,我们使用两个嵌套的for循环来计算每个dp[i][j]的值。对于dp[i][j],如果第i个物品的重量weights[i-1]大于当前背包容量j,则表示第i个物品无法放入背包中,只能继承上一个状态dp[i-1][j]的价值。否则,我们需要比较将第i个物品放入背包时所得到的价值与不放入背包时所得到的价值哪一个更大,并更新dp[i][j]为较大者。
最后,我们返回dp[n][capacity],即为前n个物品放入容量为capacity的背包中所能获得的最大价值。在主函数中,我们提供了一个测试样例来验证代码的正确性。
以下是Java语言实现的01背包问题的模板代码,包含详细的注释解释每一步的实现过程:```java
public class Knapsack {/*** 01背包问题* @param weight 物品重量数组* @param value 物品价值数组* @param capacity 背包容量* @return 最大价值*/public int knapsack(int[] weight, int[] value, int capacity) {int n = weight.length; // 物品数量// 创建一个二维数组用于存储状态转移表int[][] dp = new int[n + 1][capacity + 1];// 初始化状态转移表,当物品数量 i=0 或者背包容量 j=0 时,最大价值为0for (int i = 0; i <= n; i++) {for (int j = 0; j <= capacity; j++) {dp[i][j] = 0;}}// 动态规划填充状态转移表for (int i = 1; i <= n; i++) { // 遍历所有物品for (int j = capacity; j >= weight[i - 1]; j--) { // 遍历所有容量(倒序遍历)if (j >= weight[i - 1]) { // 当前物品可以放入背包中时,取最大价值dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);} else { // 当前物品无法放入背包中,则最优解仍然是之前的状态dp[i][j] = dp[i - 1][j];}}}return dp[n][capacity]; // 返回前n个物品能够装入容量为capacity的背包中所获得的最大价值}public static void main(String[] args) {Knapsack knapsack = new Knapsack();int[] weight = {2, 3, 4, 5}; // 物品重量数组int[] value = {3, 4, 5, 6}; // 物品价值数组int capacity = 8; // 背包容量int max_value = knapsack.knapsack(weight, value, capacity); // 最大价值System.out.println("最大价值:" + max_value);}
}希望以上代码和注释能够帮助您更好地理解01背包问题的求解过程。
以下是Java的01背包问题状态压缩代码模板:
public int knapsack(int[] weight, int[] value, int capacity) {int n = weight.length;int[] dp = new int[capacity + 1];for (int i = 0; i < n; i++) {for (int j = capacity; j >= weight[i]; j--) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}return dp[capacity];
}逆向的
与二维数组不同,状态压缩采用了一维数组 `dp` 来存储状态,其中 `dp[j]` 表示当容量为j时所能获得的最大价值。在循环方面,我们采用了正序循环的方式,保证每次计算 `dp[j]` 时,子问题中的状态都已经被更新过。
例题1:
问题描述
给定N种砝码(每种个数不限)和一个整数M,求至少需要几个砝码才可以称出刚好M克。(n<=100,m<=1000)
[输入格式]:n,m,n个整数Wi表示砝码的质量。
[输出格式]:最少需要的砝码数或impossible表示无法满足。
样例输入
5 33
12 21 3 4 6
样例输出
2
样例说明
即12+21两个砝码可以称得33
package 算法提高;import java.util.Arrays;
import java.util.Scanner;public class 砝码称重 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);//输入几种砝码int n = scanner.nextInt();//输入目标值int m = scanner.nextInt();//定义dp数组int INF = 0x7f7f7f7f;int[] dp = new int[m + 1];//初始化dp dp[i]表示重量为i时最少需要的砝码数Arrays.fill(dp, INF);dp[0]=0;//注意 0位置的是0 不要瞎弄//每个砝码的重量int[] w = new int[n];for (int i = 0; i < n; i++) {w[i] = scanner.nextInt();}for (int i = 0; i < n; i++) {for (int j = w[i]; j <= m; j++) {if (dp[j - w[i]] != INF) {dp[j] = Math.min(dp[j], dp[j - w[i]] + 1);}}}if (dp[m] == INF) {System.out.println("impossible");} else {System.out.println(dp[m]);}scanner.close();}}
问题描述:
本题的目标是求出给定N种砝码中最少需要使用多少个才能称出整数M克,其中每种砝码数量不限。
具体解决方法为使用动态规划算法,构建dp数组并通过遍历尝试各种方式计算M克质量,最后输出最少需要的砝码数或者impossible。
例题2 : Acwing 01背包
package Acwing;import java.util.Scanner;public class 零1背包 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt(), w = sc.nextInt();int a[] = new int[n + 1];int b[] = new int[n + 1];for (int i = 1; i <= n; i++) {a[i] = sc.nextInt();b[i] = sc.nextInt();}int dp[][] = new int[n + 1][w + 1];for (int i = 1; i <= n; i++) {for (int j = 0; j <=w; j++) {if (j < a[i]) {dp[i][j] = dp[i - 1][j];}elsedp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - a[i]] + b[i]);}}System.out.println(dp[n][w]);}}
2,多重背包dp(每件物品选区次数有限):
public class MultipleKnapsack {public static void main(String[] args) {int[] w = {2, 3, 4}; // 物品的体积int[] v = {1, 3, 5}; // 物品的价值int[] c = {2, 3, 1}; // 物品的数量int n = w.length; // 物品的个数int W = 7; // 背包的容量int[][] dp = new int[n + 1][W + 1]; // dp数组for (int i = 1; i <= n; i++) { // 外层循环枚举每个物品for (int j = 0; j <= W; j++) { // 内层循环枚举背包容量for (int k = 0; k <= c[i - 1] && k * w[i - 1] <= j; k++) { // 最内层循环枚举物品数量并计算状态转移方程dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - k * w[i - 1]] + k * v[i - 1]);}}}System.out.println("在背包容量为" + W + "的情况下,能够获取到的最大价值为:" + dp[n][W]);}
}
说明:
w数组表示物品的体积。
v数组表示物品的价值。
c数组表示物品的数量。
n表示物品的个数。
W表示背包的容量。
dp数组表示动态规划状态,其中dp[i][j]表示前i个物品放入容量为j的背包中能够获得的最大价值。
外层循环枚举每个物品,内层循环枚举容量,最内层循环枚举物品数量,并计算状态转移方程。
3,完全背包dp(每件物品可以选无限次):
public class CompleteKnapsack {public static void main(String[] args) {int[] w = {2, 3, 4}; // 物品的体积int[] v = {1, 3, 5}; // 物品的价值int n = w.length; // 物品的个数int W = 7; // 背包的容量int[][] dp = new int[n + 1][W + 1]; // dp数组for (int i = 1; i <= n; i++) { // 外层循环枚举每个物品for (int j = w[i - 1]; j <= W; j++) { // 内层循环枚举背包容量,并计算状态转移方程dp[i][j] = Math.max(dp[i][j], dp[i][j - w[i - 1]] + v[i - 1]);}}System.out.println("在背包容量为" + W + "的情况下,能够获取到的最大价值为:" + dp[n][W]);}
}
说明:
w数组表示物品的体积。
v数组表示物品的价值。
n表示物品的个数。
W表示背包的容量。
dp数组表示动态规划状态,其中dp[i][j]表示前i个物品放入容量为j的背包中能够获得的最大价值。
外层循环枚举每个物品,内层循环枚举容量,并计算状态转移方程。由于是完全背包,所以第i个物品可以选无限次,因此状态转移方程为dp[i][j] = Math.max(dp[i][j], dp[i][j - w[i - 1]] + v[i - 1])。
下面是用Java语言写的完全背包问题的状态压缩模板:
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);// 物品数量int n = sc.nextInt();// 背包容量int m = sc.nextInt();// 物品体积和价值数组int[] v = new int[n + 1];int[] w = new int[n + 1];for (int i = 1; i <= n; i++) {v[i] = sc.nextInt();w[i] = sc.nextInt();}// dp数组,其中第i行表示前i个物品在不超过j的背包容量时可以获得的最大价值// 因为是状态压缩,所以一维数组即可代表dp数组int[] dp = new int[m + 1];// 状态转移方程:dp[j]表示不超过背包容量j时可以获得的最大价值for (int i = 1; i <= n; i++) {for (int j = v[i]; j <= m; j++) {dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);}}System.out.println(dp[m]);}
}```
这个模板中使用了一个一维数组来存储状态。对于每个物品,我们遍历了从它自己到背包容量m之间的每个可能体积,计算出加入这个物品时可以得到的最大价值。
在这个模板中,我们并没有记录每个状态下选择了哪些物品,只记录了不同体积下可以得到的最大价值。如果需要知道具体选择了哪些物品来得到这个最大价值,可以进一步修改代码。
4,序列dp
1,LCS代码模板:
public class LCS {public static int lcs(String str1, String str2) {int m = str1.length();int n = str2.length();int[][] dp = new int[m + 1][n + 1];for (int i = 0; i <= m; i++) {for (int j = 0; j <= n; j++) {if (i == 0 || j == 0) {dp[i][j] = 0;} else if (str1.charAt(i - 1) == str2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[m][n];}public static void main(String[] args) {String str1 = "AGGTAB";String str2 = "GXTXAYB";System.out.println("Length of LCS is: " + lcs(str1, str2));}
}这里使用的是动态规划算法来求解LCS问题。在以上代码中,lcs函数接受两个字符串作为参数并返回它们的最长公共子序列的长度。我们首先初始化一个二维数组 dp,其中第一行和第一列都置为零。然后我们通过比较字符串中字符是否相等,来填充剩余部分的dp数组。
最后,我们返回 dp[m][n],其中 m 和 n 分别是两个字符串的长度。在主函数中,我们提供了两个字符串来测试我们的代码
2,LIS(最长上升子序列)问题的代码模板:
public class LIS {public static int lis(int[] nums) {int n = nums.length;int[] dp = new int[n];Arrays.fill(dp, 1);for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}}int maxLen = 0;for (int len : dp) {maxLen = Math.max(maxLen, len);}return maxLen;}public static void main(String[] args) {int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};System.out.println("The length of the longest increasing subsequence is: " + lis(nums));}
}
在以上代码中,我们定义了一个函数 lis 接受一个整数数组作为参数,并返回该数组的最长上升子序列的长度。我们首先初始化一个大小为n的数组dp,其中dp[i]表示以数字nums[i]结尾的最长上升子序列长度。
然后,我们使用两个嵌套for循环来计算每个dp[i]的值。对于dp[i],我们比较它与前面各个数nums[j]是否存在递增关系,如果存在,则更新dp[i]=dp[j]+1。
最后,我们遍历所有dp[i]并返回其中的最大值,即为最长上升子序列的长度。在主函数中,我们提供了一个整数数组来测试我们的代码。
5,计数dp
以下是Java计数dp的模板:
public class CountingDP {public static void main(String[] args) {int n = 10; // 数字范围为1到nint target = 30; // 目标数字int[] nums = {2, 3, 5}; // 可选择的数字数组int[] dp = new int[target + 1]; // dp数组dp[0] = 1;for (int i = 0; i < nums.length; i++) { // 外层循环枚举可选择的数字for (int j = nums[i]; j <= target; j++) { // 内层循环枚举目标数字,并计算状态转移方程dp[j] += dp[j - nums[i]];}}System.out.println("在" + n + "以内,由" + Arrays.toString(nums) + "组成的和为" + target + "的序列个数为:" + dp[target]);}
}
说明:
n表示数字范围为1到n。
target表示目标数字。
nums表示可选择的数字数组。
dp数组表示动态规划状态,其中dp[i]表示由给定的可选数字组成和为i的序列个数。
外层循环枚举可选择的数字,内层循环枚举目标数字,并计算状态转移方程。由于可以重复使用数字,因此状态转移方程为dp[j] += dp[j - nums[i]]。最终dp[target]即为由给定的可选数字组成和为目标数字的序列个数。
6,状态压缩dp
状态压缩dp是一种优化dp的算法,它主要是通过压缩状态来减小动态规划的状态空间,从而降低时间复杂度。Java中实现状态压缩dp也很简单,下面是一份模板代码:
// 状态压缩dp模板
public static int stateCompressDP(int[][] cost) {int n = cost.length;int m = 1 << n; // 状态数int[] dp = new int[m];Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0;for (int s = 0; s < m; s++) {for (int i = 0; i < n; i++) {if ((s & (1 << i)) == 0) { // 当前状态未访问过i节点for (int j = 0; j < n; j++) {if ((s & (1 << j)) != 0) { // 当前状态已经被访问过j节点dp[s | (1 << i)] = Math.min(dp[s | (1 << i)], dp[s] + cost[j][i]);}}}}}return dp[m - 1];
}
这份代码主要是求解一个图中所有节点之间的最短距离,其中cost[i][j]表示第i个节点到第j个节点的距离。在代码中,我们先计算出状态总数m(即2^n),然后用一个一维数组dp来存储状态对应的最短距离。在状态转移时,我们遍历所有节点,如果当前状态未访问过i节点,且已经访问过j节点,则更新dp数组。
注意,在Java中我们可以使用位运算符来实现状态压缩dp的计算。例如,“(s & (1 << i))”表示将数字s的第i位取出来进行运算。此外,我们还需要预先给dp数组赋值一个最大值(例如Integer.MAX_VALUE),以便在初始化时区分已经计算完成的结果与未计算完成的结果。
希望这份代码能够帮助到你!
7,数位dp
Java数位dp模板是一种用于解决数位相关问题的算法模板,通常用于计算一个数的各个数位上数字之和、寻找一个区间内满足某些条件的数的个数等问题。
以下是Java数位dp模板的代码:
public static int dfs(int pos, int sum, int limit) {if (pos == -1) return sum; // 边界条件if (!limit && dp[pos][sum] != -1) return dp[pos][sum]; // 记忆化搜索int maxDigit = limit ? digits[pos] : 9; // 限制最大值int res = 0;for (int i = 0; i <= maxDigit; i++) {res += dfs(pos - 1, sum + i, limit && i == maxDigit);}if (!limit) dp[pos][sum] = res; // 记录状态,避免重复计算return res;
}
其中,pos表示当前处理的数位,sum表示当前已经累加的数字和,limit表示是否达到了最大值。接下来对每一行具体进行解释。
首先判断是否到达了边界条件 pos == -1 ,如果到达则返回累加后的结果。
其次判断是否需要进行记忆化搜索。当 limit 为 false 并且 dp[pos][sum] 不等于 -1,则说明已经计算过该状态,并将其保存在 DP 数组中。如果存在该状态,则直接返回该状态对应的值。
然后,我们需要计算当前位置可以取到的最大数字。当 limit 为 true 时,我们只能取到该位置上的数字。当 limit 为 false 时,我们可以取到0~9之间的所有数字。
接下来使用for循环枚举下一位可以取到的所有数字,并进行递归调用。这里需要注意一下 limit && i == maxDigit 这个条件,它表示如果当前位置取到的数字等于上限,那么下一位只能取更小的数字。
最后,如果 limit 为 false,则我们将计算结果 res 保存在 DP 数组中,避免重复计算。而如果 limit 为 true,则不需要记录结果,因为每次都需要重新计算。
总而言之,Java数位dp模板是一个常用的处理数位相关问题的算法模板。它可以避免递归层数过多、数据规模太大而导致的爆栈或超时等问题。
8,区间dp
for (int len = 2; len <= n; len++) { // 枚举区间长度for (int i = 1; i + len - 1 <= n; i++) { // 枚举左端点int j = i + len - 1; // 计算右端点for (int k = i; k < j; k++) { // 枚举分割点dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k+1][j] + calc(i, j)); // 转移方程}}
}
其中,n表示序列的长度,i和j表示当前枚举的区间起始点和终止点,k表示当前枚举的分割点。接下来对每一行具体进行解释。
首先枚举区间长度 len ,从2开始到n为止。这里需要注意,当 len=1 时,该子问题已经被计算过了,直接跳过即可。
然后枚举左端点 i ,注意循环终止条件应为 (i + len - 1) <= n ,以保证子问题不越界。
接下来计算右端点 j ,直接令 j = i + len - 1 即可。
接着枚举分割点 k ,注意循环终止条件应为 k < j ,以保证分割点在区间内部。
然后根据题目要求构造转移方程,通常形如:dp[i][j] = Math.max(dp[i][j], dp[i][k] + dp[k+1][j] + calc(i, j)) 。这里需要注意一下计算的顺序,首先需要计算出子区间的DP值,然后再结合当前分割点计算出整个区间的DP值。
最后得到的是区间 [1,n] 的最优解,也可以根据题目需求更改其它左右端点的结果。
总而言之,Java区间dp模板是一个常用的解决区间问题的算法模板。除了以上代码框架外,每道具体题目还需要针对其特殊性质作相应修改。
相关文章:

动态规划总结
1,01背包dp(每件物品最多选一次): 因为背包为0 的时候,什么都装不了,所以为零 ,就是他们的最优解。 最后一个单元格为最后的答案。 01背包模板 public class Knapsack {public static int kn…...
分享:数据库存储与索引技术(一)存储模型与索引结构演变
欢迎访问 OceanBase 官网获取更多信息:https://www.oceanbase.com/ 本文来自OceanBase社区分享,仅限交流探讨。原作者马伟,长期从事互联网广告检索系统的研发,对数据库,编译器等领域也有浓厚兴趣。 文章目录综述传统单…...

ZeusAutoCode代码生成工具(开源)
ZeusAutoCode代码生成工具 一、简介 Zeus代码生成器是一款自动代码生成工具,旨在快速生成基础的CRUD代码,在此基础上也提供了一些高级功能,做到灵活配置,生成可扩展性强的代码。 后端是基于springboot、freemarker、mybatisplu…...
算法题记录
力扣的算法题:1154 给你一个字符串 date ,按 YYYY-MM-DD 格式表示一个 现行公元纪年法 日期。返回该日期是当年的第几天。 示例 1: 输入:date “2019-01-09” 输出:9 解释:给定日期是2019年的第九天。 示例…...

章节2 行走数据江湖,只需一行代码
目录6. 函数填充,计算列6.1 excel操作6.2 pandas操作16.3 pandas操作28. 数据筛选、过滤,[绘图前的必备功课]8.1 excel操作8.2 Python操作http://sa.mentorx.net 蔓藤教育6. 函数填充,计算列 书的编号、书的名字、标价、折扣、最终价钱 最终…...
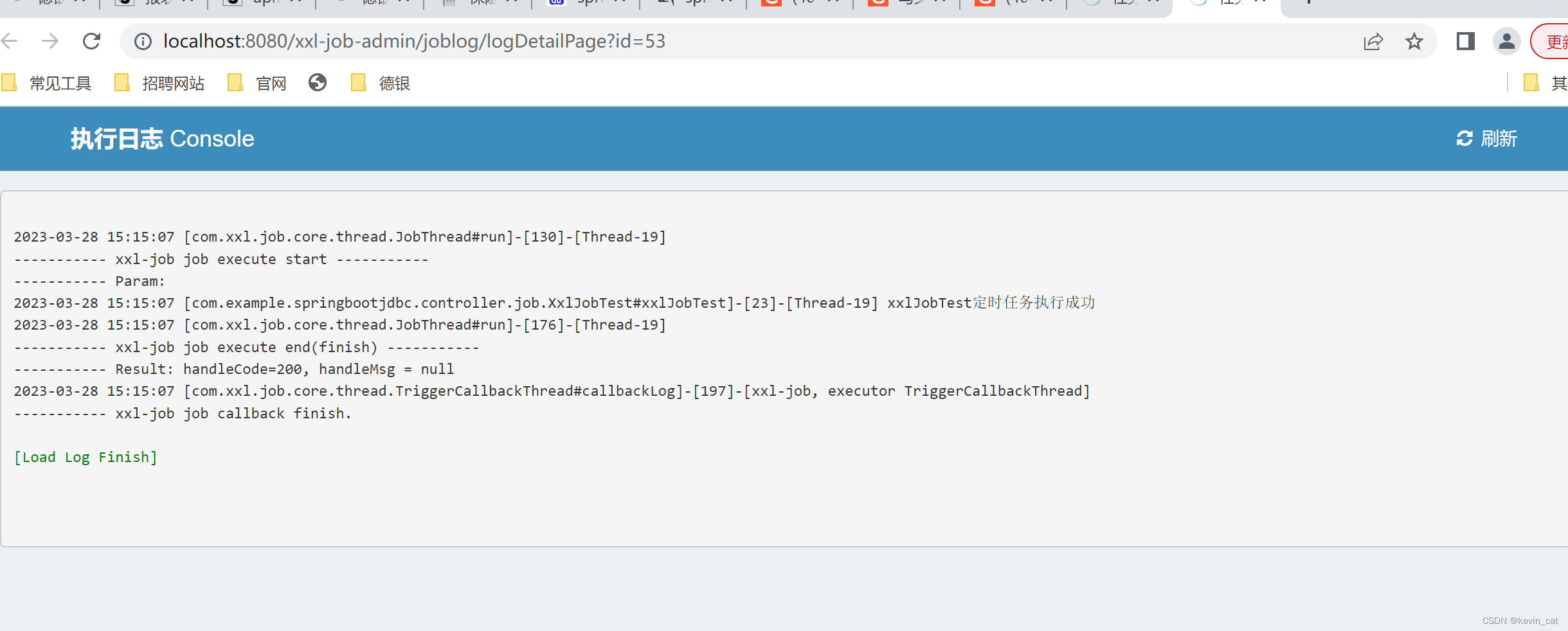
springboot集成xx-job;
概念理解: xx-job是一个分布式任务调度平台。比如你有AB两个项目。 AB的定时任务就要在xx-job上个注册。同时AB要配置对应的依赖。 所以集成xx-job要分2步骤:第一步:先搭建xx-job服务 第二步,在A项目中导包并引用。 第一步&am…...

35岁,失业6个月终于接到降薪offer:有面就面,薪酬不限,随机应变说瞎话,对奇葩面试官保持礼貌克制,为拿offer什么都能忍...
被裁后为了生存,人需要做出什么改变?一位35岁网友在失业6个月后终于拿到offer,虽然降薪到四年前的水平,但能继续养家糊口,楼主已经很满意了,并分享了自己的个人经验:1.挖掘历史项目经验…...

如何有效管理项目进度 都有哪些解决方法
项目进度管理是确保项目按时完成的关键因素之一。如果一个项目不能按时完成,那么它可能会导致成本超支、客户不满意和失去信誉等问题。因此,有效的项目进度管理至关重要。在本文中,我们将探讨如何有效管理项目进度以及可以采取哪些解决方法。…...
 光纤与电路交换)
互联网随想(三) 光纤与电路交换
光纤的 “纤”,读 xian(先),第一声,而不是 qian(千)。 光纤之于通信,就像半导体之于计算机。光纤突破了通信的电子瓶颈,就像半导体集成电路突破了计算机的电子管瓶颈一样。 但本文不是赞美光纤的,本文为反…...
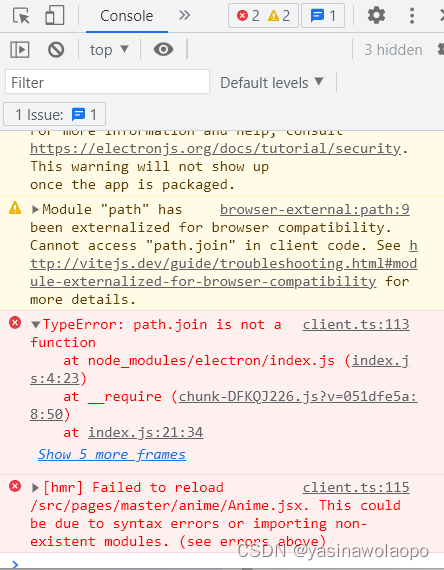
electron之旅(二)react使用
首先使用react模板 我们这里使用的是vite和yarn yarn create vite #创建vite的react-js模板初始化依赖 yarn添加依赖 state(状态管理) yarn add redux react-reduxroutes(react路由) yarn add react-router-domelectron依赖 yarn add electron vite-plugin-electron cross-env…...

ChatGPT基础知识系列之Prompt
ChatGPT基础知识系列之Prompt 在 ChatGPT 中,用户可以输入任何问题或者话题,如天气、体育、新闻等等。系统将这个输入作为一个“提示”(prompt)输入到 GPT 模型中进行处理。GPT 模型会基于其学习到的语言规律和上下文知识,生成一个自然语言回答,并返回给用户。 例如,当…...

SpringBoot3 - Spring Security 6.0 Migration
Spring Security 6.0 Migration https://docs.spring.io/spring-security/reference/5.8/migration/servlet/config.html 最近在做SpringBoot2.x到3.0的升级。其中最主要的一部分是javax -> jakartapackageName的变更,另外一部分是对一些废弃/删除的类进行替换。…...

【新2023Q2模拟题JAVA】华为OD机试 - 最少停车数
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:最少停车数 题目 特定大小的…...

《代码实例前端Vue》Security查询用户列表,用户新增
login.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>系统登录-超市订单管理系统</title><link rel"stylesheet" href"../css/style.css"><script type&qu…...
--- README翻译)
CANopenNode学习笔记(一)--- README翻译
CANopenNode学习笔记 文章目录CANopenNode学习笔记特性CANopen其他CANopenNode 流程图文件结构对象字典编辑器CANopenNode 是免费开源的CANopen协议栈。 CANopen是建立在CAN基础上的用于嵌入式控制系统的国际标准化(EN 50325-4) (CiA301)高层协议。有关CANopen的更多信息&#…...

关于Android 11、12和13服务保活问题
物联网环境,为了解决不同厂商、不同设备、不同网络情况下使用顺畅,同时也考虑到节约成本,缩小应用体积的好处,我们需要一个服务应用一直存在系统中,保活它以提供服务给其他客户端调用。 开机自启动,通过广播…...
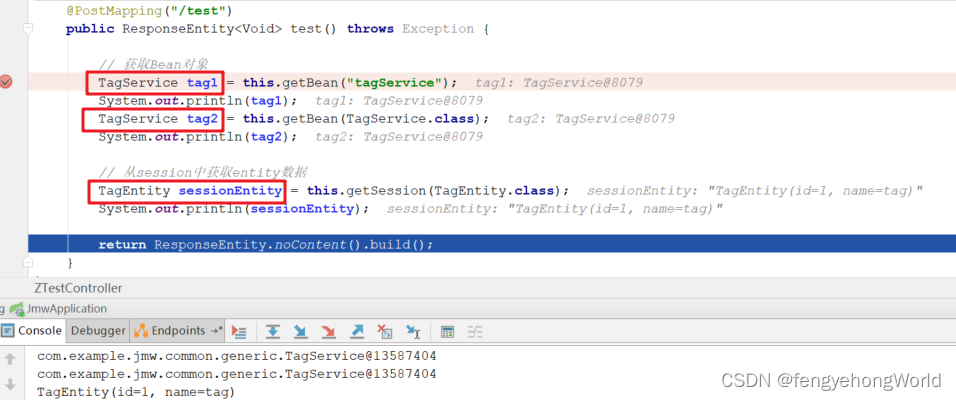
Java 泛型 使用案例
参考资料 Java 基础 - 泛型机制详解路人甲-Java泛型专题 目录一. 通用Mapper1.1 实体类1.2 Mapper基类1.3 自定义接口1.4 抽象基类Service1.5 调用二. session和bean的获取一. 通用Mapper 1.1 实体类 ⏹ Accessors(chain true): 允许链式调用 import lombok.Data; import …...

进程与线程
文章目录什么是线程线程与进程的关系线程与进程的区别什么是线程 上一篇文章中我们介绍了什么进程,我们把进程比作一个工厂,那么线程就是工厂中的流水线。引入进程的目的就是为了实现多个任务并发执行,但是如果频繁的创建销毁进程࿰…...

骑友,怎么挑选适合自己的赛事
骑友,怎么挑选适合自己的赛事一、从场地、路况、天气,各个方面了解赛事的要求。二、看完赛事,要知道自己适合参加什么样的比赛。三、通过比赛成绩,对比自己的实力。四、综合考虑自己的经济能力,根据自己的经济能力选择…...

【Java 数据结构与算法】-遍历Map和Set的方式
作者:学Java的冬瓜 博客主页:☀冬瓜的主页🌙 专栏:【Java 数据结构与算法】 文章目录一、遍历Map法一 先获取Map集合的全部key的set集合,遍历map的key的Set集合法二 把map的key和value打包成Set的key后的这个Set集合法…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
