[笔记] 仿射变换性质的代数证明
Title: [笔记] 仿射变换性质的代数证明
文章目录
- I. 仿射变换的代数表示
- II. 仿射变换的性质
- III. 同素性的代数证明
- 1. 点变换为点
- 2. 直线变换为直线
- IV. 结合性的代数证明
- 1. 直线上一点映射为直线上一点
- 2. 直线外一点映射为直线外一点
- V. 保持单比的代数证明
- VI. 平行性的代数证明
- 参考文献
I. 仿射变换的代数表示
平面上点 P ( x , y ) P(x,y) P(x,y) 经过仿射变换 T T T 变为点 P ′ ( x ′ , y ′ ) P'(x', y') P′(x′,y′), 则两点坐标 ( x , y ) (x,y ) (x,y) 和 ( x ′ , y ′ ) (x', y') (x′,y′) 之间的关系即为仿射变换的代数表示. 需注意仿射坐标系不一定是直角坐标系.
平面上的仿射变换在仿射坐标系下的代数表示为
{ x ′ = a 11 x + a 12 y + a 13 y ′ = a 21 x + a 22 y + a 23 (I-1) \left\{ \begin{aligned} x' = a_{11} x + a_{12} y + a_{13}\\ y' = a_{21} x + a_{22} y + a_{23} \end{aligned} \right. \tag{I-1} {x′=a11x+a12y+a13y′=a21x+a22y+a23(I-1)
其中
Δ = ∣ a 11 a 12 a 21 a 22 ∣ ≠ 0 (I-2) \Delta = \left|\begin{matrix}a_{11} &a_{12} \\ a_{21} & a_{22}\end{matrix}\right| \neq 0 \tag{I-2} Δ= a11a21a12a22 =0(I-2)
也就是仿射变换是可逆变换, 其逆变换可以写成
{ x = a 11 ′ x ′ + a 12 ′ y ′ + a 13 ′ y = a 21 ′ x ′ + a 22 ′ y ′ + a 23 ′ (I-3) \left\{ \begin{aligned} x = a'_{11} x' + a'_{12} y' + a'_{13}\\ y = a'_{21} x' + a'_{22} y' + a'_{23} \end{aligned} \right. \tag{I-3} {x=a11′x′+a12′y′+a13′y=a21′x′+a22′y′+a23′(I-3)
其中
Δ ′ = ∣ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ∣ ≠ 0 (I-4) \Delta' = \left|\begin{matrix}a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{matrix}\right| \neq 0 \tag{I-4} Δ′= a11′a21′a12′a22′ =0(I-4)
可知
[ a 11 a 12 a 21 a 22 ] [ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] = [ 1 0 0 1 ] (I-5) \begin{bmatrix}a_{11} &a_{12} \\ a_{21} & a_{22}\end{bmatrix} \begin{bmatrix}a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{bmatrix} = \begin{bmatrix}1 &0 \\ 0 & 1 \end{bmatrix} \tag{I-5} [a11a21a12a22][a11′a21′a12′a22′]=[1001](I-5)
及
[ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] [ a 11 a 12 a 21 a 22 ] = [ 1 0 0 1 ] (I-6) \begin{bmatrix}a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{bmatrix} \begin{bmatrix}a_{11} &a_{12} \\ a_{21} & a_{22}\end{bmatrix} = \begin{bmatrix}1 &0 \\ 0 & 1 \end{bmatrix} \tag{I-6} [a11′a21′a12′a22′][a11a21a12a22]=[1001](I-6)
II. 仿射变换的性质
- 保持同素性 (点变换为点, 直线变换为直线)
- 保持结合性 (点和直线的结合关系)
- 保持共线三点的单比不变
- 保持直线的平行性
III. 同素性的代数证明
1. 点变换为点
定义式 (I-1) 即是证明.
2. 直线变换为直线
假设有一直线方程为
a x + b y + c = 0 (III-2-1) ax + by + c =0 \tag{III-2-1} ax+by+c=0(III-2-1)
其中 a 2 + b 2 ≠ 0 a^2 + b^2 \neq 0 a2+b2=0.
在仿射变换下有式 (I-3), 代入式 (III-2-1) 得到
a ( a 11 ′ x ′ + a 12 ′ y ′ + a 13 ′ ) + b ( a 21 ′ x ′ + a 22 ′ y ′ + a 23 ′ ) + c = 0 ⇒ ( a a 11 ′ + b a 21 ′ ) x ′ + ( a a 12 ′ + b a 22 ′ ) y ′ + ( a a 13 ′ + b a 23 ′ + c ) = 0 (III-2-2) \begin{aligned} a(a'_{11} x' + a'_{12} y' + a'_{13}) + b(a'_{21} x' + a'_{22} y' + a'_{23}) + c =0\\ \Rightarrow \quad (a a'_{11}+ b a'_{21}) x' + (aa'_{12} + b a'_{22}) y' +(a a'_{13} + b a'_{23} +c) = 0 \end{aligned} \tag{III-2-2} a(a11′x′+a12′y′+a13′)+b(a21′x′+a22′y′+a23′)+c=0⇒(aa11′+ba21′)x′+(aa12′+ba22′)y′+(aa13′+ba23′+c)=0(III-2-2)
另外, 由仿射变换的可逆性质式 (I-3) 可知
∣ a 11 ′ a 21 ′ a 12 ′ a 22 ′ ∣ ≠ 0 (III-2-3) \left|\begin{matrix} a'_{11} &a'_{21} \\ a'_{12} &a'_{22} \end{matrix} \right| \neq 0 \tag{III-2-3} a11′a12′a21′a22′ =0(III-2-3)
则使得下式
[ a a 11 ′ + b a 21 ′ a a 12 ′ + b a 22 ′ ] = [ a 11 ′ a 21 ′ a 12 ′ a 22 ′ ] [ a b ] = [ 0 0 ] (III-2-4) \begin{bmatrix}a a'_{11}+ b a'_{21} \\ aa'_{12} + b a'_{22} \end{bmatrix}=\begin{bmatrix} a'_{11} &a'_{21} \\ a'_{12} &a'_{22} \end{bmatrix} \begin{bmatrix}a\\b \end{bmatrix} = \begin{bmatrix}0\\0 \end{bmatrix} \tag{III-2-4} [aa11′+ba21′aa12′+ba22′]=[a11′a12′a21′a22′][ab]=[00](III-2-4)
成立的解仅为 ( a , b ) = ( 0 , 0 ) (a, b) = (0, 0) (a,b)=(0,0), 但与条件矛盾. 故 ( a a 11 ′ + b a 21 ′ ) (a a'_{11}+ b a'_{21}) (aa11′+ba21′) 与 ( a a 12 ′ + b a 22 ′ ) (aa'_{12} + b a'_{22}) (aa12′+ba22′) 不能同时为零.
即式 (III-2-2) 中变量 x ′ x' x′ 和 y ′ y' y′ 前的系数满足
( a a 11 ′ + b a 21 ′ ) 2 + ( a a 12 ′ + b a 22 ′ ) 2 ≠ 0 (III-2-5) (a a'_{11}+ b a'_{21})^2 + (aa'_{12} + b a'_{22})^2 \neq 0 \tag{III-2-5} (aa11′+ba21′)2+(aa12′+ba22′)2=0(III-2-5)
即式 (III-2-2) 必然为直线方程. 所以直线方程经过仿射变换后仍然为直线方程, 直线经过仿射变换后仍为直线.
IV. 结合性的代数证明
1. 直线上一点映射为直线上一点
已知一点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 在直线 a x + b y + c = 0 ax+by+c =0 ax+by+c=0 上 ⟺ \Longleftrightarrow ⟺ 满足 a x 1 + b y 1 + c = 0 ax_1 +by_1 +c =0 ax1+by1+c=0.
下面证明仿射变换后的新点在仿射变换后的新直线上.
点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 经过仿射变换后得到新点 ( x 1 ′ , y 1 ′ ) (x'_1, y'_1) (x1′,y1′)
{ x 1 ′ = a 11 x 1 + a 12 y 1 + a 13 y 1 ′ = a 21 x 1 + a 22 y 1 + a 23 (IV-1-1) \left\{ \begin{aligned} x'_1 = a_{11} x_1 + a_{12} y_1 + a_{13}\\ y'_1 = a_{21} x_1 + a_{22} y_1 + a_{23} \end{aligned} \right. \tag{IV-1-1} {x1′=a11x1+a12y1+a13y1′=a21x1+a22y1+a23(IV-1-1)
由同素性式 (III-2-2), 直线 a x + b y + c = 0 ax+by+c =0 ax+by+c=0 经过仿射变换后得到新的直线方程
( a a 11 ′ + b a 21 ′ ) x ′ + ( a a 12 ′ + b a 22 ′ ) y ′ + ( a a 13 ′ + b a 23 ′ + c ) = 0 (IV-1-2) (a a'_{11}+ b a'_{21}) x' + (aa'_{12} + b a'_{22}) y' +(a a'_{13} + b a'_{23} +c) = 0 \tag{IV-1-2} (aa11′+ba21′)x′+(aa12′+ba22′)y′+(aa13′+ba23′+c)=0(IV-1-2)
将仿射变换后的新点坐标式 (IV-1-1) 代入上式的左侧得到
LHS = ( a a 11 ′ + b a 21 ′ ) ( a 11 x 1 + a 12 y 1 + a 13 ) ‾ + ( a a 12 ′ + b a 22 ′ ) ( a 21 x 1 + a 22 y 1 + a 23 ) ‾ + ( a a 13 ′ + b a 23 ′ + c ) = ( a a 11 ′ + b a 21 ′ ) a 11 x 1 + ( a a 12 ′ + b a 22 ′ ) a 21 x 1 + ( a a 11 ′ + b a 21 ′ ) a 12 y 1 + ( a a 12 ′ + b a 22 ′ ) a 22 y 1 + ( a a 11 ′ + b a 21 ′ ) a 13 + ( a a 12 ′ + b a 22 ′ ) a 23 + ( a a 13 ′ + b a 23 ′ + c ) = ( a a 11 ′ a 11 + a a 12 ′ a 21 + b a 21 ′ a 11 + b a 22 ′ a 21 ) x 1 + ( a a 11 ′ a 12 + a a 12 ′ a 22 + b a 21 ′ a 12 + b a 22 ′ a 22 ) y 1 + ( a a 11 ′ a 13 + a a 12 ′ a 23 + a a 13 ′ + b a 21 ′ a 13 + b a 22 ′ a 23 + b a 23 ′ ) + c = [ a b ] [ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] [ a 11 a 21 ] x 1 + [ a b ] [ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] [ a 12 a 22 ] y 1 + [ a b ] { [ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] [ a 13 a 23 ] + [ a 13 ′ a 23 ′ ] } + c (IV-1-3) \begin{aligned} \text{LHS}\ =\ &(a a'_{11}+ b a'_{21})\underline{(a_{11} x_1 + a_{12} y_1 + a_{13})} + (aa'_{12} + b a'_{22}) \underline{(a_{21} x_1 + a_{22} y_1 + a_{23})} + (a a'_{13} + b a'_{23} +c)\\ =\ & (a a'_{11}+ b a'_{21})a_{11} x_1 + (aa'_{12} + b a'_{22}) a_{21} x_1 \\ {+} & (a a'_{11}+ b a'_{21}) a_{12} y_1 +(aa'_{12} + b a'_{22}) a_{22} y_1 \\ {+}& (a a'_{11}+ b a'_{21}) a_{13} + (aa'_{12} + b a'_{22}) a_{23} + (a a'_{13} + b a'_{23} +c)\\ =\ & (a a'_{11}a_{11}+ aa'_{12} a_{21} + b a'_{21}a_{11} + b a'_{22} a_{21}) x_1 \\ {+}& (a a'_{11}a_{12}+ a a'_{12} a_{22} + b a'_{21} a_{12} + b a'_{22} a_{22}) y_1\\ {+}& (a a'_{11} a_{13}+ aa'_{12} a_{23} + a a'_{13} + b a'_{21} a_{13} + b a'_{22} a_{23} + b a'_{23}) \\ +& c\\ =\ & \begin{bmatrix} a &b\end{bmatrix} \begin{bmatrix} a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{bmatrix} \begin{bmatrix} a_{11} \\ a_{21}\end{bmatrix} x_1 \\ {+}& \begin{bmatrix} a &b\end{bmatrix} \begin{bmatrix} a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{bmatrix} \begin{bmatrix} a_{12} \\ a_{22}\end{bmatrix} y_1 \\ {+}& \begin{bmatrix} a &b\end{bmatrix} \left\{\begin{bmatrix} a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{bmatrix} \begin{bmatrix} a_{13} \\ a_{23}\end{bmatrix}+ \begin{bmatrix} a'_{13} \\ a'_{23}\end{bmatrix}\right\} \\ {+}& c \end{aligned} \tag{IV-1-3} LHS = = ++= +++= +++(aa11′+ba21′)(a11x1+a12y1+a13)+(aa12′+ba22′)(a21x1+a22y1+a23)+(aa13′+ba23′+c)(aa11′+ba21′)a11x1+(aa12′+ba22′)a21x1(aa11′+ba21′)a12y1+(aa12′+ba22′)a22y1(aa11′+ba21′)a13+(aa12′+ba22′)a23+(aa13′+ba23′+c)(aa11′a11+aa12′a21+ba21′a11+ba22′a21)x1(aa11′a12+aa12′a22+ba21′a12+ba22′a22)y1(aa11′a13+aa12′a23+aa13′+ba21′a13+ba22′a23+ba23′)c[ab][a11′a21′a12′a22′][a11a21]x1[ab][a11′a21′a12′a22′][a12a22]y1[ab]{[a11′a21′a12′a22′][a13a23]+[a13′a23′]}c(IV-1-3)
由式 (I-6) 可知
[ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] [ a 11 a 21 ] = [ 1 0 ] (IV-1-4) \begin{bmatrix}a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{bmatrix} \begin{bmatrix}a_{11} \\ a_{21} \end{bmatrix} = \begin{bmatrix}1 \\ 0 \end{bmatrix} \tag{IV-1-4} [a11′a21′a12′a22′][a11a21]=[10](IV-1-4)
和
[ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] [ a 12 a 22 ] = [ 0 1 ] (IV-1-5) \begin{bmatrix}a'_{11} &a'_{12} \\ a'_{21} & a'_{22}\end{bmatrix} \begin{bmatrix}a_{12} \\ a_{22}\end{bmatrix} = \begin{bmatrix}0 \\ 1 \end{bmatrix} \tag{IV-1-5} [a11′a21′a12′a22′][a12a22]=[01](IV-1-5)
由仿射变换式 (I-1) 可知原点 ( 0 , 0 ) (0,0) (0,0) 的像为 ( a 13 , a 23 ) (a_{13}, a_{23}) (a13,a23), 即
{ x o ′ = a 11 0 + a 12 0 + a 13 = a 13 y o ′ = a 21 0 + a 22 0 + a 23 = a 23 (IV-1-6) \left\{ \begin{aligned} x'_{o} = a_{11} 0 + a_{12} 0 + a_{13} = a_{13}\\ y'_{o} = a_{21} 0 + a_{22} 0 + a_{23} = a_{23} \end{aligned} \right. \tag{IV-1-6} {xo′=a110+a120+a13=a13yo′=a210+a220+a23=a23(IV-1-6)
相反地, 原点的像 ( a 13 , a 23 ) (a_{13}, a_{23}) (a13,a23) 经过仿射变换逆映射式 (I-3) 后回到原点, 即
{ 0 = a 11 ′ a 13 + a 12 ′ a 23 + a 13 ′ 0 = a 21 ′ a 13 + a 22 ′ a 23 + a 23 ′ (IV-1-7) \left\{ \begin{aligned} 0 = a'_{11} a_{13} + a'_{12} a_{23} + a'_{13}\\ 0 = a'_{21} a_{13} + a'_{22} a_{23} + a'_{23} \end{aligned} \right. \tag{IV-1-7} {0=a11′a13+a12′a23+a13′0=a21′a13+a22′a23+a23′(IV-1-7)
上式写成矩阵形式为
[ a 11 ′ a 12 ′ a 21 ′ a 22 ′ ] [ a 13 a 23 ] + [ a 13 ′ a 23 ′ ] = [ 0 0 ] (IV-1-8) \begin{bmatrix}a'_{11} & a'_{12}\\a'_{21} &a'_{22} \end{bmatrix} \begin{bmatrix}a_{13} \\ a_{23} \end{bmatrix} + \begin{bmatrix}a'_{13} \\ a'_{23} \end{bmatrix} = \begin{bmatrix}0 \\0 \end{bmatrix} \tag{IV-1-8} [a11′a21′a12′a22′][a13a23]+[a13′a23′]=[00](IV-1-8)
将式 (IV-1-4)、(IV-1-5)、(IV-1-8) 代入式 (IV-1-3), 即仿射变换后的新点坐标式 (IV-1-1) 左侧为
LHS = [ a b ] [ 1 0 ] x 1 + [ a b ] [ 0 1 ] y 1 + [ a b ] [ 0 0 ] + c = a x 1 + b y 1 + c = 0 (IV-1-9) \begin{aligned} \text{LHS}\ =\ & \begin{bmatrix} a &b\end{bmatrix} \begin{bmatrix} 1 \\ 0\end{bmatrix} x_1 {+} \begin{bmatrix} a &b\end{bmatrix} \begin{bmatrix} 0 \\ 1\end{bmatrix} y_1 {+} \begin{bmatrix} a &b\end{bmatrix} \begin{bmatrix} 0 \\ 0\end{bmatrix} {+} c\\ =\ & a x_1 {+} b y_1 {+} c\\ = \ &0 \end{aligned} \tag{IV-1-9} LHS = = = [ab][10]x1+[ab][01]y1+[ab][00]+cax1+by1+c0(IV-1-9)
也就是说, 点 ( x 1 , y 1 ) (x_1, y_1) (x1,y1) 经过仿射变换后得到的新点 ( x 1 ′ , y 1 ′ ) (x'_1, y'_1) (x1′,y1′) 满足直线 a x + b y + c = 0 ax+by+c =0 ax+by+c=0 进过仿射变换后得到的新直线方程式 (IV-1-2).
即直线上一点经过仿射变换后仍然在经过仿射变换后的直线上.
2. 直线外一点映射为直线外一点
如果存在仿射变换 φ \varphi φ 可以将直线 l l l 外一点 P P P 映射为直线 l ′ l' l′ 上一点 P ′ P' P′, 即
φ : l ↦ l ′ φ : P ↦ P ′ P ∉ l , P ′ ∈ l ′ (IV-2-1) \varphi:l \mapsto l'\\ \varphi:P \mapsto P' \\ P \notin l, P' \in l'\tag{IV-2-1} φ:l↦l′φ:P↦P′P∈/l,P′∈l′(IV-2-1)
因为仿射变换的逆变换仍然是仿射变换, 即 φ − 1 \varphi^{-1} φ−1 仍然是仿射变换.
由已证明的 “直线上一点映射为直线上一点”, 可知经过逆仿射变换 φ − 1 \varphi^{-1} φ−1, 直线 l ′ l' l′ 上点 P ′ P' P′ 映射为直线 l l l 上点 P P P.
即已知像点 P ′ P' P′ 在直线 l ′ l' l′ 上时, 原像点 P P P 必在直线 l l l 上.
假设矛盾, 证毕.
V. 保持单比的代数证明
共线三点 P ( x , y ) P(x,y) P(x,y)、 P 1 ( x 1 , y 1 ) P_1(x_1, y_1) P1(x1,y1)、 P 2 ( x 2 , y 2 ) P_2(x_2, y_2) P2(x2,y2) 的单比为
( P 1 P 2 P ) = x − x 1 x − x 2 = y − y 1 y − y 2 = k (V-1) (P_1 P_2 P) = \frac{x-x_1}{x - x_2}=\frac{y-y_1}{y-y_2}=k \tag{V-1} (P1P2P)=x−x2x−x1=y−y2y−y1=k(V-1)
即
x − x 1 = k ( x − x 2 ) y − y 1 = k ( y − y 2 ) (V-2) {x-x_1}= k(x - x_2)\\ {y-y_1}= k(y-y_2) \tag{V-2} x−x1=k(x−x2)y−y1=k(y−y2)(V-2)
经过仿射变换后得到 P ′ ( x ′ , y ′ ) P'(x',y') P′(x′,y′)、 P 1 ′ ( x 1 ′ , y 1 ′ ) P'_1(x'_1, y'_1) P1′(x1′,y1′)、 P 2 ′ ( x 2 ′ , y 2 ′ ) P'_2(x'_2, y'_2) P2′(x2′,y2′). 由仿射变换的结合性可知, P ′ P' P′、 P 1 ′ P'_1 P1′、 P 2 ′ P'_2 P2′ 三点仍然共线. 共线三点可计算单比
( P 1 ′ P 2 ′ P ′ ) = x ′ − x 1 ′ x ′ − x 2 ′ = y ′ − y 1 ′ y ′ − y 2 ′ = k ′ (V-3) (P'_1 P'_2 P') = \frac{x'-x'_1}{x' - x'_2}=\frac{y'-y'_1}{y'-y'_2}=k' \tag{V-3} (P1′P2′P′)=x′−x2′x′−x1′=y′−y2′y′−y1′=k′(V-3)
由仿射变换式 (I-1) 并结合式 (V-2), 可知
k ′ = x ′ − x 1 ′ x ′ − x 2 ′ = a 11 x + a 12 y + a 13 − ( a 11 x 1 + a 12 y 1 + a 13 ) a 11 x + a 12 y + a 13 − ( a 11 x 2 + a 12 y 2 + a 13 ) = a 11 ( x − x 1 ) + a 12 ( y − y 1 ) a 11 ( x − x 2 ) + a 12 ( y − y 2 ) = k a 11 ( x − x 2 ) + k a 12 ( y − y 2 ) a 11 ( x − x 2 ) + a 12 ( y − y 2 ) = k (V-4) \begin{aligned} k' &= \frac{x'-x'_1}{x' - x'_2} \\ &= \frac{a_{11} x + a_{12} y + a_{13} - (a_{11} x_1 + a_{12} y_1 + a_{13})}{a_{11} x + a_{12} y + a_{13} - (a_{11} x_2 + a_{12} y_2 + a_{13})}\\ &= \frac{a_{11} (x-x_1) + a_{12} (y-y_1)}{a_{11} (x-x_2) + a_{12} (y-y_2)}\\ &= \frac{k a_{11} (x-x_2) + k a_{12} (y-y_2)}{a_{11} (x-x_2) + a_{12} (y-y_2)}\\ &= k \end{aligned}\tag{V-4} k′=x′−x2′x′−x1′=a11x+a12y+a13−(a11x2+a12y2+a13)a11x+a12y+a13−(a11x1+a12y1+a13)=a11(x−x2)+a12(y−y2)a11(x−x1)+a12(y−y1)=a11(x−x2)+a12(y−y2)ka11(x−x2)+ka12(y−y2)=k(V-4)
即单比保持不变.
VI. 平行性的代数证明
已知两条直线 l 1 l_1 l1 和 l 2 l_2 l2 平行, 则该两条直线的方程可写为
{ l 1 : a x + b y + c 1 = 0 l 2 : a x + b y + c 2 = 0 (VI-1) \left\{ \begin{aligned} l_1: ax+by+c_1=0\\ l_2: ax+by+c_2=0 \end{aligned} \right. \tag{VI-1} {l1:ax+by+c1=0l2:ax+by+c2=0(VI-1)
其中 c 1 ≠ c 2 c_1 \neq c_2 c1=c2. (注意仿射坐标系不一定为直角坐标系)
由同素性证明中式 (III-1-2) , 直线 l 1 l_1 l1 和 l 2 l_2 l2 经过仿射变换的方程式分别为
l 1 ′ : ( a a 11 ′ + b a 21 ′ ) x ′ + ( a a 12 ′ + b a 22 ′ ) y ′ + ( a a 13 ′ + b a 23 ′ + c 1 ) = 0 l 2 ′ : ( a a 11 ′ + b a 21 ′ ) x ′ + ( a a 12 ′ + b a 22 ′ ) y ′ + ( a a 13 ′ + b a 23 ′ + c 2 ) = 0 l'_1: (a a'_{11}+ b a'_{21}) x' + (aa'_{12} + b a'_{22}) y' +(a a'_{13} + b a'_{23} +c_1) = 0\\ l'_2: (a a'_{11}+ b a'_{21}) x' + (aa'_{12} + b a'_{22}) y' +(a a'_{13} + b a'_{23} +c_2) = 0 l1′:(aa11′+ba21′)x′+(aa12′+ba22′)y′+(aa13′+ba23′+c1)=0l2′:(aa11′+ba21′)x′+(aa12′+ba22′)y′+(aa13′+ba23′+c2)=0
其中 a a 13 ′ + b a 23 ′ + c 1 ≠ a a 13 ′ + b a 23 ′ + c 2 a a'_{13} + b a'_{23} +c_1 \neq a a'_{13} + b a'_{23} +c_2 aa13′+ba23′+c1=aa13′+ba23′+c2, 而两者的方向数相同.
可知经过仿射变换后 l 1 ′ l'_1 l1′ 和 l 2 ′ l'_2 l2′ 仍然平行.
参考文献
[1] 梅向明, 刘增贤, 王汇淳, 王智秋, 高等几何(第四版), 高等教育出版社, 2020
版权声明:本文为博主原创文章,遵循 CC 4.0 BY 版权协议,转载请附上原文出处链接和本声明。
本文链接:https://blog.csdn.net/woyaomaishu2/article/details/142771571
本文作者:wzf@robotics_notes
相关文章:

[笔记] 仿射变换性质的代数证明
Title: [笔记] 仿射变换性质的代数证明 文章目录 I. 仿射变换的代数表示II. 仿射变换的性质III. 同素性的代数证明1. 点变换为点2. 直线变换为直线 IV. 结合性的代数证明1. 直线上一点映射为直线上一点2. 直线外一点映射为直线外一点 V. 保持单比的代数证明VI. 平行性的代数证明…...

遥感影像-语义分割数据集:sar水体数据集详细介绍及训练样本处理流程
原始数据集详情 简介:该数据集由WHU-OPT-SAR数据集整理而来,覆盖面积51448.56公里,分辨率为5米。据我们所知,WHU-OPT-SAR是第一个也是最大的土地利用分类数据集,它融合了高分辨率光学和SAR图像,并进行了充…...

极狐GitLab 发布安全补丁版本 17.4.1、17.3.4、17.2.8
GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 学习极狐GitLab 的相关资料: 极狐GitLab 官网极狐…...

汽车管理系统中使用函数
目录 setupUisetEnabledcurrentText()setTextsetFocus()query.exec(...)addWidgetconnect setupUi setupUi() 是 ui 对象的一个成员函数,它的作用是根据 .ui 文件中的设计,将设计好的组件(如按钮、文本框、布局等)添加到当前的窗…...

大数据分析入门概述
大数据分析入门概述 本文旨在为有意向学习数据分析、数据开发等大数据方向的初学者提供一个学习指南,当然如果你希望通过视频课程的方式快速入门,B站UP主戴戴戴师兄的课程质量很高,并且适合初学者快速入门。本文的目的旨在为想要了解大数据但…...
提示工程、微调和 RAG
自众多大型语言模型(LLM)和高级对话模型发布以来,人们已经运用了各种技术来从这些 AI 系统中提取所需的输出。其中一些方法会改变模型的行为来更好地贴近我们的期望,而另一些方法则侧重于增强我们查询 LLM 的方式,以提…...

自动化测试中如何高效进行元素定位!
前言 在自动化测试中,元素定位是一项非常重要的工作。良好的元素定位可以帮助测试人员处理大量的测试用例,加快测试进度,降低工作负担。但是在实际的测试工作中,我们常常遇到各种各样的定位问题,比如元素定位失败、元…...

UE5数字人制作平台使用及3D模型生成
第10章 数字人制作平台使用及3D模型生成 在数字娱乐、虚拟现实(VR)、增强现实(AR)等领域,高质量的3D模型是数字内容创作的核心。本章将引导你了解如何使用UE5(Unreal Engine 5)虚幻引擎这一强大…...

Linux进程被占用如何杀死进程
文章目录 前言一、根据名称进行查找程序所占用的端口号二、杀死进程总结 前言 由于Linux中,校园网登录的时候容易出现端口被占用,如何快速查找程序所占用的端口号。 提示:以下是本篇文章正文内容,下面案例可供参考 一、根据名称…...

详解Xilinx JESD204B PHY层端口信号含义及动态切换线速率(JESD204B五)
点击进入高速收发器系列文章导航界面 Xilinx官方提供了两个用于开发JESD204B的IP,其中一个完成PHY层设计,另一个完成传输层的逻辑,两个IP必须一起使用才能正常工作。 7系列FPGA只能使用最多12通道的JESD204B协议,线速率为1.0至12.…...

Java面试——场景题
1.如何分批处理数据? 1.使用LIMIT和OFFSET子句: 这是最常用的分批查询方法。例如,你可以使用以下SQL语句来分批查询数据: SELECT * FROM your_table LIMIT 1000 OFFSET 0; 分批查询到的数据在后端进行处理,达到分批…...

xss-labs靶场第一关测试报告
目录 一、测试环境 1、系统环境 2、使用工具/软件 二、测试目的 三、操作过程 1、注入点寻找 2、使用hackbar进行payload测试 3、绕过结果 四、源代码分析 五、结论 一、测试环境 1、系统环境 渗透机:本机(127.0.0.1) 靶 机:本机(127.0.0.…...
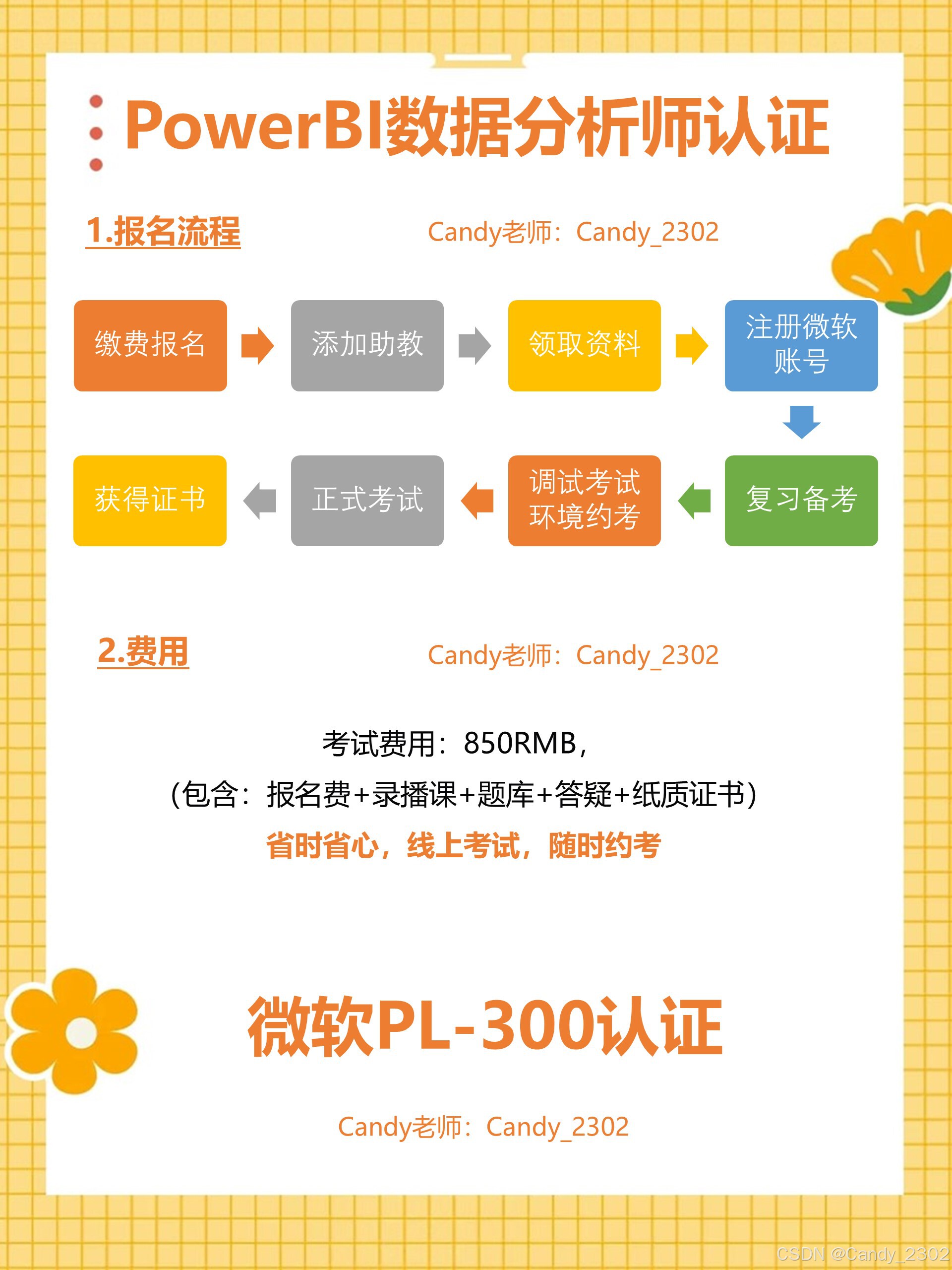
微软PowerBI认证!数据分析师入门级证书备考攻略来啦
#微软PowerBI认证!数据分析师入门级证书! 😃Power BI是一种强大的数据可视化和分析工具,学习Power BI,能提高数据的分析能力,将数据转化为有意义的见解,并支持数据驱动的决策制定。 ㅤ ✨微软P…...

上海AI Lab视频生成大模型书生.筑梦环境搭建推理测试
引子 最近视频生成大模型层出不穷,上海AI Lab推出新一代视频生成大模型 “书生・筑梦 2.0”(Vchitect 2.0)。根据官方介绍,书生・筑梦 2.0 是集文生视频、图生视频、插帧超分、训练系统一体化的视频生成大模型。OK,那就让我们开始吧。 一、模…...

3D看车如何实现?有哪些功能特点和优势?
3D看车是一种创新的汽车展示方式,它利用三维建模和虚拟现实技术,将汽车以更真实、更立体的形式呈现在消费者面前。 一、3D看车的实现方式 1、三维建模: 通过三维建模技术,按照1:1的比例还原汽车外观,包括车身线条、细…...

Pytorch中不会自动传播梯度的操作有哪些?
在 PyTorch 中,某些生成张量的操作本身不会创建与计算图相关联的梯度信息。这些操作通常用于初始化张量,并且默认情况下不需要进行梯度计算。以下是一些常见的不会自动传播梯度的张量生成操作: 数值初始化操作: torch.linspace():…...

【设计模式】软件设计原则——开闭原则里氏替换单一职责
开闭原则内容引出 开闭原则 定义:一个软件实体,类,函数,模块;对扩展开放,对修改关闭。用抽象构建框架,用实现扩展细节。可以提高软件的可复用性和可维护性。 开发新功能时,尽量不修…...
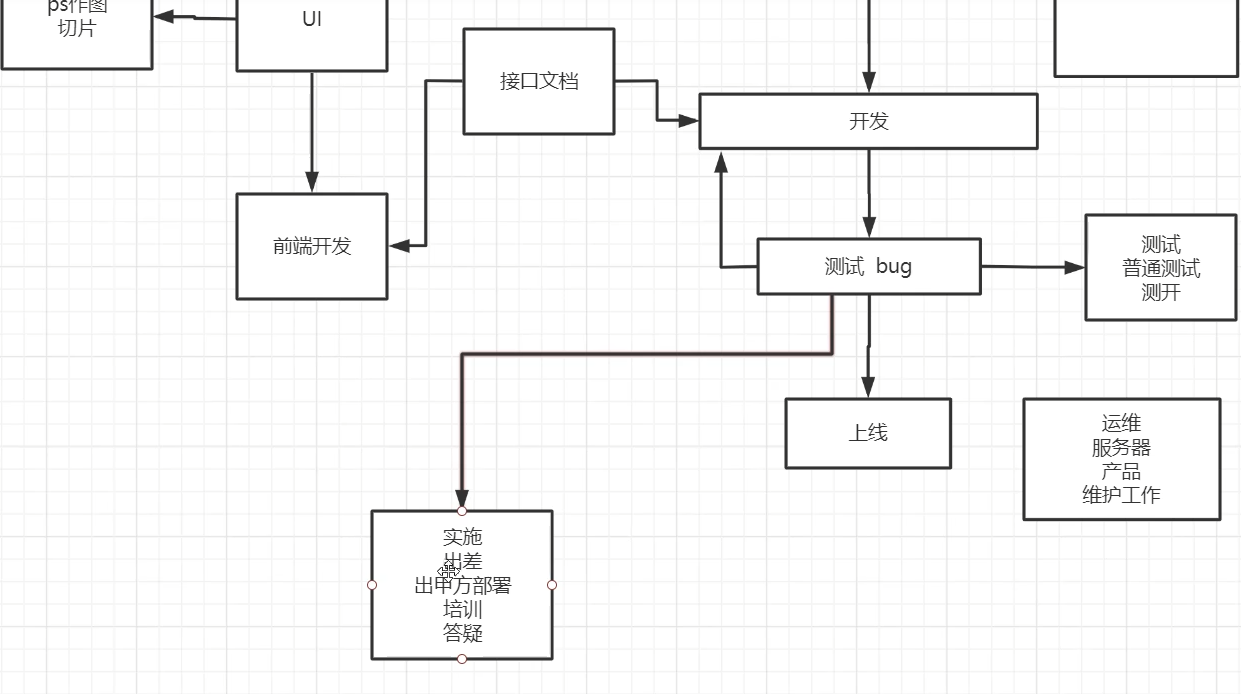
项目完整开发的流程
流程 1.设计产品 2.写需求文档 2.1需求分析,后端设计数据库,建表,客户沟通,说完签字,留证据,防止后面扯皮,和防止后续变需求重新写业务 3.画原型图,也就是草图,初始的…...

性能测试学习6:jmeter安装与基本配置/元件/线程组介绍
一.JDK安装 官网:https://www.oracle.com/ 二.Jmeter安装 官网:http://jmeter.apache.org/download_jmeter.cgi 下载zip包,zip后缀那个才是Windows系统的jmeter 三.Jmeter工作目录介绍 四.Jmeter功能 1)修改默认配置-汉化 2&am…...

大数据ETL数据提取转换和加载处理
什么是 ETL? 提取转换加载(英语:Extract, transform, load,简称ETL),用来描述将资料从来源端经过抽取、转置、加载至目的端的过程。ETL一词较常用在数据仓库,但其对象并不限于数据仓库。 ETL&…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

Win系统权限提升篇UAC绕过DLL劫持未引号路径可控服务全检项目
应用场景: 1、常规某个机器被钓鱼后门攻击后,我们需要做更高权限操作或权限维持等。 2、内网域中某个机器被钓鱼后门攻击后,我们需要对后续内网域做安全测试。 #Win10&11-BypassUAC自动提权-MSF&UACME 为了远程执行目标的exe或者b…...

Netty自定义协议解析
目录 自定义协议设计 实现消息解码器 实现消息编码器 自定义消息对象 配置ChannelPipeline Netty提供了强大的编解码器抽象基类,这些基类能够帮助开发者快速实现自定义协议的解析。 自定义协议设计 在实现自定义协议解析之前,需要明确协议的具体格式。例如,一个简单的…...

__VUE_PROD_HYDRATION_MISMATCH_DETAILS__ is not explicitly defined.
这个警告表明您在使用Vue的esm-bundler构建版本时,未明确定义编译时特性标志。以下是详细解释和解决方案: 问题原因: 该标志是Vue 3.4引入的编译时特性标志,用于控制生产环境下SSR水合不匹配错误的详细报告1使用esm-bundler…...
