【python机器学习】线性回归 拟合 欠拟合与过拟合 以及波士顿房价预估案例
文章目录
- 线性回归之波士顿房价预测案例 欠拟合与过拟合
- 线性回归API 介绍:
- 波士顿房价预测
- 数据属性:
- 机器学习代码实现
- 拟合 过拟合 欠拟合 模拟 及处理方法(正则化处理)
- 导包
- 定义函数表示欠拟合
- 定义函数表示拟合
- 定义函数表示过拟合
- 正则化处理过拟合
- L1正则化
- L2正则化
线性回归之波士顿房价预测案例 欠拟合与过拟合
线性回归API 介绍:

波士顿房价预测
数据属性:

机器学习代码实现
1.导入库
from sklearn.preprocessing import StandardScaler # 特征处理
from sklearn.model_selection import train_test_split # 数据集划分
from sklearn.linear_model import LinearRegression # 正规方程的回归模型
from sklearn.linear_model import SGDRegressor # 梯度下降的回归模型
from sklearn.metrics import mean_squared_error # 均方误差评估
# from sklearn.datasets import load_boston # 数据
注意在新版本sklearn中上述读取数据方式失效通过下面方法读取数据
import pandas as pd
import numpy as npdata_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
2.模型代码实现
# 正规方程法
def demo01():# 数据集划分x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2)# 特征工程 特征预处理transfer = StandardScaler() # 创建标准化对象# 标准化 训练集 测试集x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 模型训练estimator = LinearRegression() # 线性回归模型对象estimator.fit(x_train, y_train)# 模型预测y_predict = estimator.predict(x_test)# 和测试集的标签进行比较# 1.均方误差print("均方误差的误差为:", mean_squared_error(y_test, y_predict))# 2.平均绝对误差print("平均绝对误差的误差为:", mean_absolute_error(y_test, y_predict))# 3.均方根误差print("均方根误差的误差为:", root_mean_squared_error(y_test, y_predict))# 梯度下降法
def demo02():# 数据集划分x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.2)# 特征工程 特征预处理transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.transform(x_test)# 模型训练estimator = SGDRegressor(max_iter=1000, learning_rate='constant',eta0=0.001) # 获取梯度下降模型对象 max_iter 最大次数 eta0 学习率 ,learning_rate='constant' 设置学习率为常数estimator.fit(x_train, y_train)# 模型预测y_predict = estimator.predict(x_test)# 模型评估# 1.均方误差print("均方误差的误差为:", mean_squared_error(y_test, y_predict))# 2.平均绝对误差print("平均绝对误差的误差为:", mean_absolute_error(y_test, y_predict))# 3.均方根误差print("均方根误差的误差为:", root_mean_squared_error(y_test, y_predict))
运行结果 上为标准函数 下为梯度下降

拟合 过拟合 欠拟合 模拟 及处理方法(正则化处理)

导包
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error # 计算均方误差
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge, Lasso
定义函数表示欠拟合
欠拟合出现的原因:学习到数据的特征过少
解决方法: 【从数据、模型、算法的角度去想解决方案】
添加其他特征
有时出现欠拟合是因为特征项不够导致的,可以添加其他特征项来解决
“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段
添加多项式特征项
模型过于简单时的常用套路,例如将线性模型通过添加二次项或三次项使模型泛化能力更强
def demo01():# 准备数据# 准备噪声np.random.seed(21)# x 表示特征x = np.random.uniform(-3, 3, size=100)# y 表示目标值 线性关系 y = 0.5x^2 +x + 2 + 正态分布 + 噪声y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)# 模型训练# 创建线性回归方程对象estimator = LinearRegression()# 训练estimator.fit(x.reshape(-1, 1), y)# 根据模型预测y_predict = estimator.predict(x.reshape(-1, 1))# 模型评估print('均方误差', mean_squared_error(y, y_predict))# 这里看到均方误差正常 但是实际上欠拟合 画图plt.scatter(x, y) # x,y散点图plt.plot(x, y_predict, color='red') # 拟合回归线 即预测值plt.show()

根据数据可视化结果发现 均方误差正常,但是可视化结果表示模型欠拟合,用一次方程拟合二次
需要提升模型维度,增加特征值
定义函数表示拟合
在demo01 的基础上 对x 增加维度 即 拼接x和x^2 使得拟合回归线为2次方程
def demo02():# 准备数据# 准备噪声np.random.seed(21)# x 表示特征x = np.random.uniform(-3, 3, size=100)# y 表示目标值 线性关系 y = 0.5x^2 +x + 2 + 正态分布 + 噪声y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)x_reshape = x.reshape(-1, 1)x2 = np.hstack([x_reshape, x_reshape ** 2]) # 拼接x和x的平方 增加模型维度# 模型训练# 创建线性回归方程对象estimator = LinearRegression()# 训练estimator.fit(x2, y)# 根据模型预测y_predict = estimator.predict(x2)# 模型评估print('均方误差', mean_squared_error(y, y_predict))# 这里看到均方误差正常 但是实际上欠拟合 画图plt.scatter(x, y) # x,y散点图plt.plot(x, y_predict, color='red') # 拟合回归线 即预测值plt.show()
数据可视化结果虽然拟合曲线出来了,但是因为没有对散点排序,导致绘制时没有按顺序连接

def demo02():# 准备数据# 准备噪声np.random.seed(21)# x 表示特征x = np.random.uniform(-3, 3, size=100)# y 表示目标值 线性关系 y = 0.5x^2 +x + 2 + 正态分布 + 噪声y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)x_reshape = x.reshape(-1, 1)x2 = np.hstack([x_reshape, x_reshape ** 2]) # 拼接x和x的平方 增加模型维度# 模型训练# 创建线性回归方程对象estimator = LinearRegression()# 训练estimator.fit(x2, y)# 根据模型预测y_predict = estimator.predict(x2)# 模型评估print('均方误差', mean_squared_error(y, y_predict))# 这里看到均方误差正常 但是实际上欠拟合 画图plt.scatter(x, y) # x,y散点图plt.plot(np.sort(x), y_predict[np.argsort(x)], color='red') # 拟合回归线 即预测值plt.show()
排序后正确的拟合线

定义函数表示过拟合
过拟合出现的原因:
- 原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法:
- 重新清洗数据
- 对于过多异常点数据、数据不纯的地方再处理
- 增大数据的训练量
- 对原来的数据训练的太过了,增加数据量的情况下,会缓解
正则化
- 对原来的数据训练的太过了,增加数据量的情况下,会缓解
- 解决模型过拟合的方法,在机器学习、深度学习中大量使用
减少特征维度,防止维灾难 - 由于特征多,样本数量少,导致学习不充分,泛化能力差。
在demo02 函数上继续增加维度 会导致模型会兼顾每个测试点,导致过拟合
def demo03():# 准备数据# 准备噪声np.random.seed(21)# x 表示特征x = np.random.uniform(-3, 3, size=100)# y 表示目标值 线性关系 y = 0.5x^2 +x + 2 + 正态分布 + 噪声y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)x_reshape = x.reshape(-1, 1)x2 = np.hstack([x_reshape, x_reshape ** 2, x_reshape ** 3, x_reshape ** 4, x_reshape ** 5, x_reshape ** 6, x_reshape ** 7,x_reshape ** 8, x_reshape ** 9, x_reshape ** 10, x_reshape ** 11, x_reshape ** 12, x_reshape ** 13,x_reshape ** 14, x_reshape ** 15, x_reshape ** 16, x_reshape ** 17, x_reshape ** 18,x_reshape ** 19]) # 拼接x和x的平方 增加模型维度# 模型训练# 创建线性回归方程对象estimator = LinearRegression()# 训练estimator.fit(x2, y)# 根据模型预测y_predict = estimator.predict(x2)# 模型评估print('均方误差', mean_squared_error(y, y_predict))# 这里看到均方误差正常 但是实际上欠拟合 画图plt.scatter(x, y) # x,y散点图plt.plot(np.sort(x), y_predict[np.argsort(x)], color='red') # 拟合回归线 即预测值plt.show()
过拟合展示

正则化处理过拟合

L1正则化

在demo03基础上 将线性回归模型对象改为l1正则化线性回归模型对象
def demo04():np.random.seed(21)# x 表示特征x = np.random.uniform(-3, 3, size=100)# y 表示目标值 线性关系 y = 2x + 3 + 噪声y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)# 模型训练# 创建 线性回归 L1 正则化 模型对象estimator = Lasso(alpha=0.1) # alpha 正则化参数 值越大 正则化程度越大# 对数据集做处理# print("处理前:", x)X = x.reshape(-1, 1)# print("处理后:", X)# 拼接 x 和 x 的平方X2 = np.hstack([X, X ** 2, X ** 3, X ** 4, X ** 5, X ** 6, X ** 7, X ** 8, X ** 9, X ** 10, X ** 11, X ** 12, X ** 13, X ** 14,X ** 15, X ** 16, X ** 17, X ** 18, X ** 19, X ** 20])# print("处理后:", X2)# 训练estimator.fit(X2, y)# 预测y_predict = estimator.predict(X2)print("预测值:", y_predict)# 模型评估print('均方误差', mean_squared_error(y, y_predict))# 数据可视化 绘制图像print(np.sort(x))print(np.argsort(x))plt.scatter(x, y) # 基于原始的x,y 绘制散点图plt.plot(np.sort(x), y_predict[np.argsort(x)], color='red') # 原始的x , y 预测值 绘制折线图(拟合回归线)plt.show()
l1正则化过后的曲线

L1正则化通过改变权重,并将特殊点的权重完全改为0来避免过拟合问题
L2正则化

将模型改为L2正则化线性回归模型
def demo05():# 准备数据# 准备噪声np.random.seed(21)# x 表示特征x = np.random.uniform(-3, 3, size=100)# y 表示目标值 线性关系 y = 2x + 3 + 噪声y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)# 模型训练# 创建 线性回归 L2 正则化 模型对象estimator = Ridge(alpha=0.1) # alpha 正则化参数 值越大 正则化程度越大# 对数据集做处理# print("处理前:", x)X = x.reshape(-1, 1)# print("处理后:", X)# 拼接 x 和 x 的平方X2 = np.hstack([X, X ** 2, X ** 3, X ** 4, X ** 5, X ** 6, X ** 7, X ** 8, X ** 9, X ** 10, X ** 11, X ** 12, X ** 13, X ** 14,X ** 15, X ** 16, X ** 17, X ** 18, X ** 19, X ** 20])# print("处理后:", X2)# 训练estimator.fit(X2, y)# 预测y_predict = estimator.predict(X2)print("预测值:", y_predict)# 模型评估print('均方误差', mean_squared_error(y, y_predict))# 数据可视化 绘制图像print(np.sort(x))print(np.argsort(x))plt.scatter(x, y) # 基于原始的x,y 绘制散点图plt.plot(np.sort(x), y_predict[np.argsort(x)], color='red') # 原始的x , y 预测值 绘制折线图(拟合回归线)plt.show()


相关文章:

【python机器学习】线性回归 拟合 欠拟合与过拟合 以及波士顿房价预估案例
文章目录 线性回归之波士顿房价预测案例 欠拟合与过拟合线性回归API 介绍:波士顿房价预测数据属性:机器学习代码实现 拟合 过拟合 欠拟合 模拟 及处理方法(正则化处理)导包定义函数表示欠拟合定义函数表示拟合定义函数表示过拟合 正则化处理过拟合L1正则化L2正则化 线性回归之波…...

IT招聘乱象的全面分析
近年来,IT行业的招聘要求似乎越来越苛刻,甚至有些不切实际。许多企业在招聘时,不仅要求前端工程师具备UI设计能力,还希望后端工程师精通K8S服务器运维,更有甚至希望研发经理掌握所有前后端框架和最新开发技术。这种招聘…...

一入递归深似海,算法之美无止境
最近在刷leetcode hot100,在写二叉树中最大路径和的时候,看到了一个佬对递归的理解,深受启发,感觉自己对于递归的题又行了!!! 这里给大家分享一下(建立大家先去尝试一下这道题再来看 124. 二叉树中的最大路径和 二叉树中的 路径 被定义为一条节点序列,序列中每…...

进程的状态的理解(概念+Linux)
文章目录 进程的状态并行和并发物理和逻辑 时间片进程具有独立性等待的本质运行阻塞标记挂起等待 Linux下的进程状态(一)运行状态(R - running)(二)睡眠状态(S - sleeping)ÿ…...

Apache Linkis + OceanBase:如何提升数据分析效率
计算中间件 Apache Linkis 构建了一个计算中间件层,以实现上层应用程序和底层数据引擎之间的连接、治理和编排。目前,已经支持通过数据源的功能,实现用户通过Linkis 对接并使用 OceanBase数据库。 本文详细阐述了在 Apache Linkis v1.3.2中&a…...
Day01-postgresql数据库基础入门培训
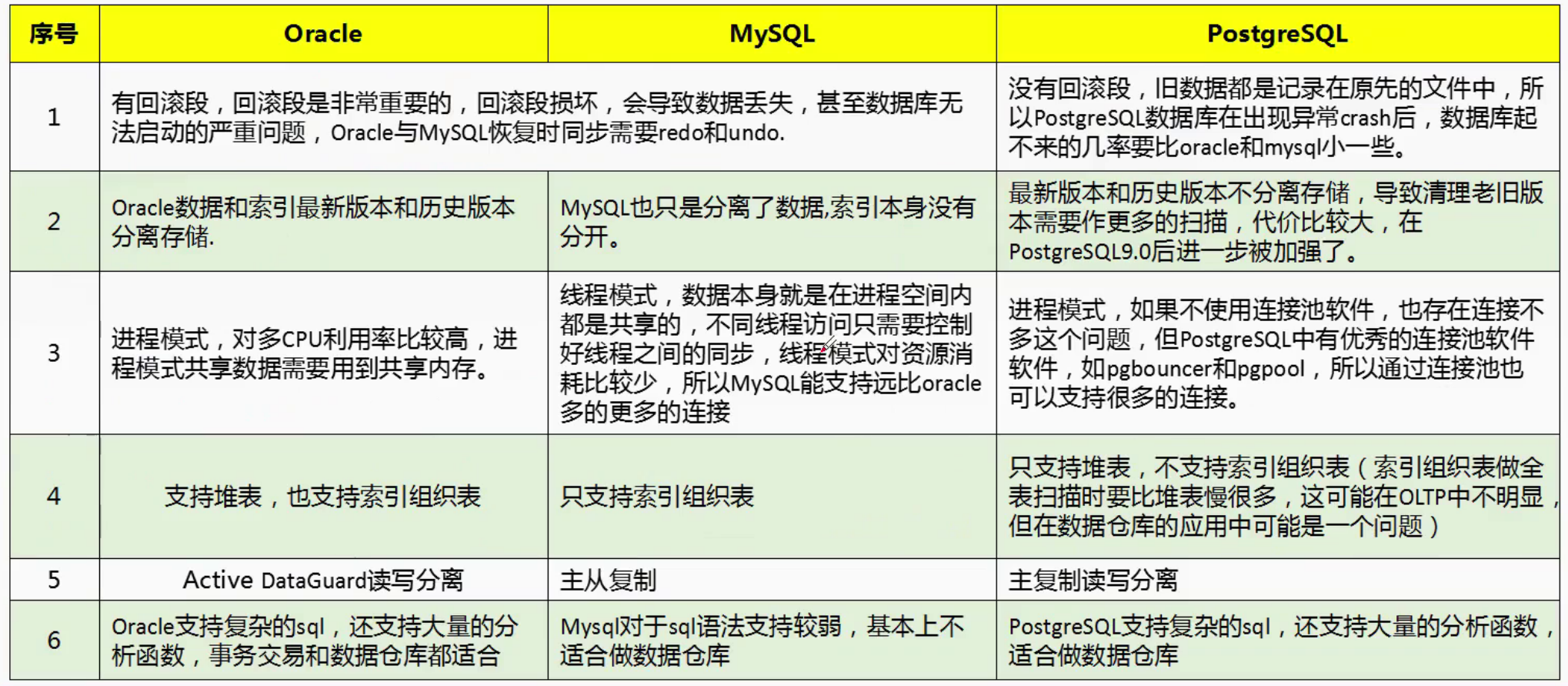
Day01-postgresql数据库基础入门培训 1、PostgresQL数据库简介2、PostgreSQL行业生态应用3、PostgreSQL版本发展与特性4、PostgreSQL体系结构介绍5、PostgreSQL与MySQL的区别6、PostgreSQL与Oracle、MySQL的对比 1、PostgresQL数据库简介 PostgreSQL【简称:PG】是加…...

打卡第四天 P1081 [NOIP2012 提高组] 开车旅行
今天是我打卡第四天,做个省选/NOI−题吧(#^.^#) 原题链接:[NOIP2012 提高组] 开车旅行 - 洛谷 题目描述 输入格式 输出格式 输入输出样例 输入 #1 4 2 3 1 4 3 4 1 3 2 3 3 3 4 3 输出 #1 1 1 1 2 0 0 0 0 0 输入 #2 10 4 5 6 1 …...

Jenkins Pipline流水线
提到 CI 工具,首先想到的就是“CI 界”的大佬--]enkjns,虽然在云原生爆发的年代,蹦出来了很多云原生的 CI 工具,但是都不足以撼动 Jenkins 的地位。在企业中对于持续集成、持续部署的需求非常多,并且也会经常有-些比较复杂的需求,此时新生的 CI 工具不足以支撑这些很…...

鸿蒙harmonyos next flutter混合开发之开发FFI plugin
创建FFI plugin summation,默认创建的FFI plugin是求两个数的和 flutter create --templateplugin_ffi summation --platformsandroid,ios,ohos 创建my_application flutter create --org com.example my_application 在my_application项目中文件pubspec.yaml引…...

oracle数据库安装和配置
Oracle数据库安装 一、安装前的准备 系统要求: 硬件:内存至少1GB(推荐2GB以上),硬盘至少10GB的可用空间,CPU至少2核心。 操作系统:支持Oracle版本的Windows(如Windows 10或更高版本…...

猫玖破密啦
题目: 终究还是猫哥:3d5a3a0cfff7fb2e29194c0b7a89f284ff19a8 玖离:收到消息Oh,what_is_the_flag 玖离:7468655f666c61675f69735f666c13556d2cf2faec1e2d0f330b7dcceea1c62cb2 终究还是猫哥:收到消息************************************ 已…...

SpringBoot框架:服装生产管理的现代化工具
摘 要 本协力服装厂服装生产管理系统设计目标是实现协力服装厂服装生产的信息化管理,提高管理效率,使得协力服装厂服装生产管理作规范化、科学化、高效化。 本文重点阐述了协力服装厂服装生产管理系统的开发过程,以实际运用为开发背景&#…...

Android Preference的使用以及解析
简单使用 values.arrays.xml <?xml version"1.0" encoding"utf-8"?> <resources><string-array name"list_entries"><item>Option 1</item><item>Option 2</item><item>Option 3</item&…...

HCIP——GRE和MGRE
目录 VPN GRE GRE环境的搭建 GRE的报文结构 GRE封装和解封装报文的过程 GRE配置编辑 R1 R2 GRE实验编辑 MGRE 原理 MGRE的配置 R1 R2 R3 R4 查看映射表 抓包 MGRE环境下的RIP网络 综合练习编辑 VPN 说到GRE,我们先来说个大…...

微信小程序——音乐播放器
一、界面设计 播放页面: 显示当前播放歌曲的封面图片、歌曲名称、歌手名称。有播放 / 暂停按钮、上一首、下一首按钮。进度条显示播放进度,可以拖动进度条调整播放位置。音量调节滑块。 歌曲列表页面: 展示歌曲列表,包括歌曲名称、…...

OceanBase 4.x 部署实践:如何从单机扩展至分布式部署
OceanBase 4.x 版本支持2种部署模式:单机部署与分布式部署,同时支持从单机平滑扩展至分布式架构。这样,可以有效解决小型业务向大型业务转型时面临的扩展难题,降低了机器资源的成本。 以下将详述如何通过命令行,实现集…...

大数据新视界 --大数据大厂之TeZ 大数据计算框架实战:高效处理大规模数据
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...
)
docker详解介绍+基础操作 (三)
1.docker 存储引擎 Overlay: 一种Union FS文件系统,Linux 内核3.18后支持 Overlay2:Overlay的升级版,docker的默认存储引擎,需要磁盘分区支持d-type功能,因此需要系统磁盘的额外支持。 关于 d-type 传送…...

【大语言模型-论文精读】谷歌-BERT:用于语言理解的预训练深度双向Transformers
【大语言模型-论文精读】谷歌-BERT:用于语言理解的预训练深度双向Transformers 目录 文章目录 【大语言模型-论文精读】谷歌-BERT:用于语言理解的预训练深度双向Transformers目录0. 引言1. 简介2 相关工作2.1 基于特征的无监督方法2.2 无监督微调方法2.3…...

【Java】集合中单列集合详解(一):Collection与List
目录 引言 一、Collection接口 1.1 主要方法 1.1.1 添加元素 1.1.2 删除元素 1.1.3 清空元素 1.1.4 判断元素是否存在 1.1.5 判断是否为空 1.1.6 求取元素个数 1.2 遍历方法 1.2.1 迭代器遍历 1.2.2 增强for遍历 1.2.3 Lambda表达式遍历 1.2.4 应用场景 二、…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
