【C++第十七章】二叉搜索树

【C++第十七章】二叉搜索树

二叉搜索树的介绍🧐

  二叉搜索树又称二叉排序树，它可能是空树，也可能是具有以下性质的二叉树：

1. 若它的左子树不为空，则左子树上的所有节点的值小于根节点的值
2. 若它的右子树不为空，则右子树上的所有节点的值大于根节点的值
3. 它的左右子树也分别为二叉搜索树

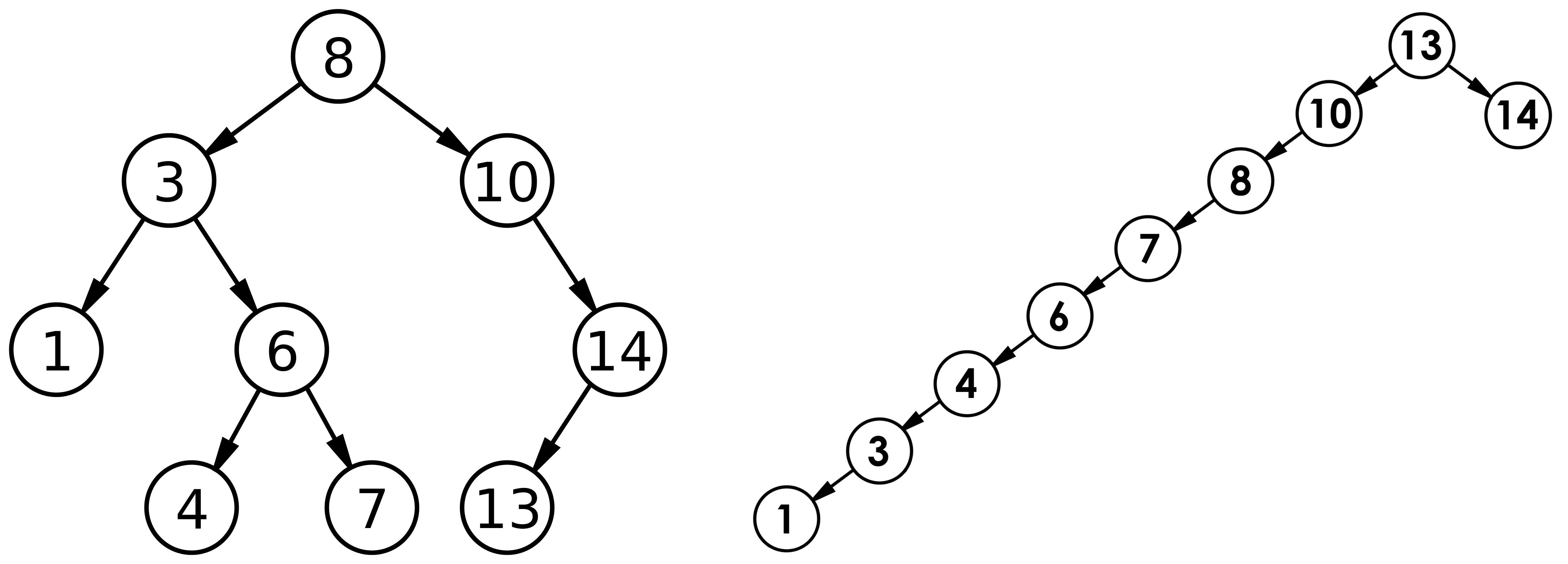
  如我们将如下数组放入二叉搜索树中，会得到这样的结构，可以发现，它的中序是有序排列的。

int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};

二叉搜索树的查找🧐

  从根开始比较查找，比根大就往右走，比根小就往左走，最多走树的高度次，如果走到空了还没找到，就是不存在。

参考代码：

bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;
}

二叉搜索树的插入🧐

  当树为空时，直接增加新的节点，赋值给root指针，如果不为空，则按性质插入，小于根在左，大于根在右。

参考代码

bool Insert(const K& key)
{if (_root == nullptr) //第一次插入{_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}//链接cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else if (parent->_key > key){parent->_left = cur;}return true;
}

二叉搜索树的删除🧐

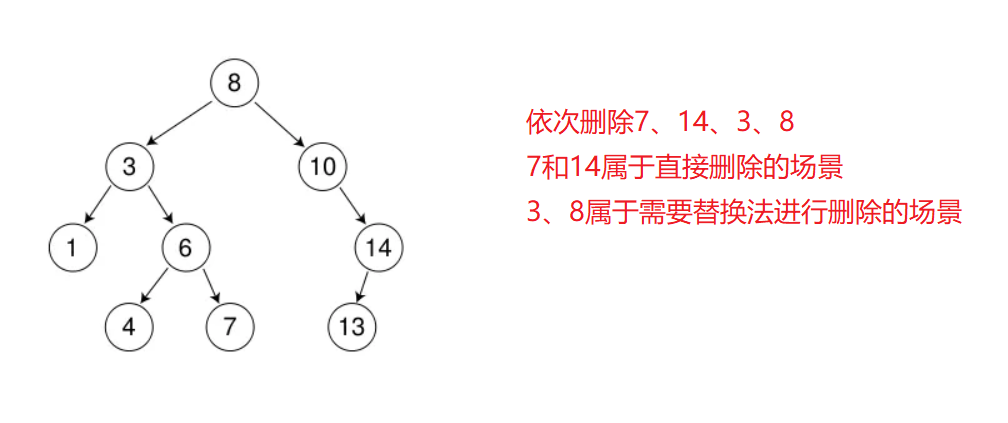
  首先查找元素是否存在，不存在就直接返回，存在则要分四种情况分析：

1. 要删除的节点没有孩子节点
2. 要删除的节点只有左孩子节点
3. 要删除的节点只有右孩子节点
4. 要删除的节点有左右孩子节点

  而第一种情况可以和第二种和第三种合并起来，所以真正情况有三种：

1. 删除该节点且使被删除的节点的双亲节点指向被删除节点的左孩子节点——直接删除
2. 删除该节点且使被删除的节点的双亲节点指向被删除节点的右孩子节点——直接删除
3. 在它的右子树中寻找中序下的第一个节点(最小值)，用它的值填补到被删除节点中(交换)，再处理该节点的删除——替换法删除

参考代码

bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else //找到了，可以开始删除了{if (cur->_left == nullptr) //左为空{if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr) //右为空{if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else //左右都不为空{//右树的最小结点(最左结点)Node* subLeft = cur->_right;Node* parent = cur; //parent直接等于cur，防止删除根时parent为空导致交换出错while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key); //找到了就交换if (subLeft == parent->_left) //看节点在左边还是右边{parent->_left = subLeft->_right;}else{parent->_right = subLeft->_right;}}return true;}}return false;
}

全部代码🧐

namespace key
{template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree() = default; //c++11强制生成默认构造bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else //默认情况下，不允许给重复值{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else //找到了，可以开始删除了{if (cur->_left == nullptr) //左为空{if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr) //右为空{if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else //左右都不为空{//右树的最小结点(最左结点)Node* subLeft = cur->_right;Node* parent = cur; //parent直接等于cur，防止删除根时parent为空导致交换出错while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left){parent->_left = subLeft->_right;}else{parent->_right = subLeft->_right;}}return true;}}return false;}~BSTree(){cout << "~destory" << endl;Destory(_root);}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* NewRoot = new Node(root->_key);NewRoot->_left = Copy(root->_left);NewRoot->_right = Copy(root->_right);return NewRoot;}void Destory(Node*& root){if (root == nullptr)return;Destory(root->_left);Destory(root->_right);delete root;root = nullptr;}Node* _root = nullptr;};
}

二叉搜索树的应用——K模型、KV模型🧐

  K模型：K模型即只有Key作为关键码，结构中只需要存储Key即可。比如给一个名字判断他在不在名单中。在上面介绍的二叉搜索树就是K模型。

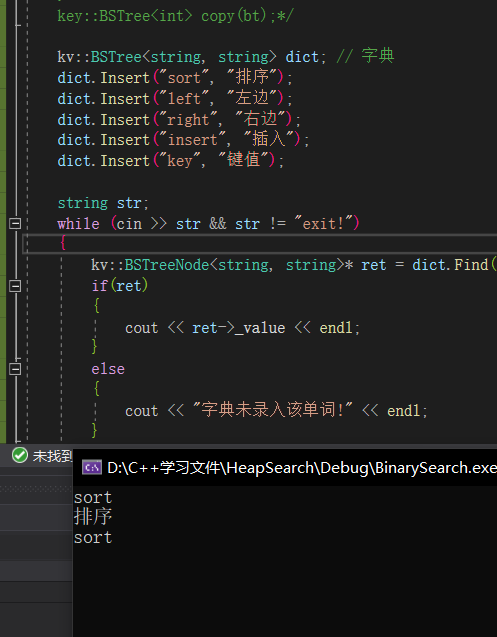
  KV模型：让每一个Key都有一个对应的Value，即**<Key,Value>**的键值对。比如词典的中英对应，输入英文可以直接查找到对应的中文意思，再比如统计次数，可以快速找到一个单词出现的次数。

  KV模型只需要在K模型上进行修改即可。

namespace kv
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:BSTree() = default; //c++11强制生成默认构造bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key,value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else //默认情况下，不允许给重复值{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else //找到了，可以开始删除了{if (cur->_left == nullptr) //左为空{if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr) //右为空{if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else //左右都不为空{//右树的最小结点(最左结点)Node* subLeft = cur->_right;Node* parent = cur; //parent直接等于cur，防止删除根时parent为空导致交换出错while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left){parent->_left = subLeft->_right;}else{parent->_right = subLeft->_right;}}return true;}}return false;}private:void Destory(Node*& root){if (root == nullptr)return;Destory(root->_left);Destory(root->_right);delete root;root = nullptr;}Node* _root = nullptr;};
}

二叉搜索树的性能分析🧐

  二叉搜索树插入与删除都需要先进行查找，最优情况下，二叉搜索树为完全二叉树，时间复杂度为O(logN)。最坏情况下，二叉搜索树为单支树，时间复杂度为O(N)。当为单支树时，二叉搜索树的性能优势就没有了，所以我们后续会学习AVL树和红黑树，对二叉搜索树进行优化。

结尾👍

  以上便是二叉搜索树的全部内容，如果有疑问或者建议都可以私信笔者交流，大家互相学习，互相进步！🌹