LeetCode326_326. 3 的幂
LeetCode326_326. 3 的幂
一、描述
给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 3 的幂次方需满足:存在整数 x 使得 n == 3的x次方
示例 1:
输入:n = 27
输出:true
示例 2:
输入:n = 0
输出:false
示例 3:
输入:n = 9
输出:true
示例 4:
输入:n = 45
输出:false
提示:
-的2的31次方 <= n <= 2的31次方 - 1
二、题解
方法一:试除法
//试除法//AC Your runtime beats 64.91 % of java submissions.//21038 / 21038 test cases passed Status: Accepted Runtime: 70 ms//其实就是判读一个数可不可以有 n个3 相乘得到 和263题思路很像public boolean isPowerOfThree(int n) {boolean res = false;if (n <= 0) {return false;} else {while (n % 3 == 0)n /= 3;if (n == 1) {res = true;}}return res;}
LeetCode 242. 有效的字母异位词
LeetCode 257. 二叉树的所有路径
LeetCode 258. 各位相加
LeetCode 263. 丑数
LeetCode 268. 丢失的数字
LeetCode 283. 移动零
LeetCode 287. 寻找重复数
LeetCode 290. 单词规律
LeetCode 292. Nim 游戏
LeetCode 303. 区域和检索 - 数组不可变
LeetCode 326. 3 的幂
LeetCode 342. 4的幂
声明:
题目版权为原作者所有。文章中代码及相关语句为自己根据相应理解编写,文章中出现的相关图片为自己实践中的截图和相关技术对应的图片,若有相关异议,请联系删除。感谢。转载请注明出处,感谢。
By luoyepiaoxue2014
B站: https://space.bilibili.com/1523287361 点击打开链接
微博: http://weibo.com/luoyepiaoxue2014 点击打开链接
相关文章:

LeetCode326_326. 3 的幂
LeetCode326_326. 3 的幂 一、描述 给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。 整数 n 是 3 的幂次方需满足:存在整数 x 使得 n 3的x次方 示例 1: 输…...
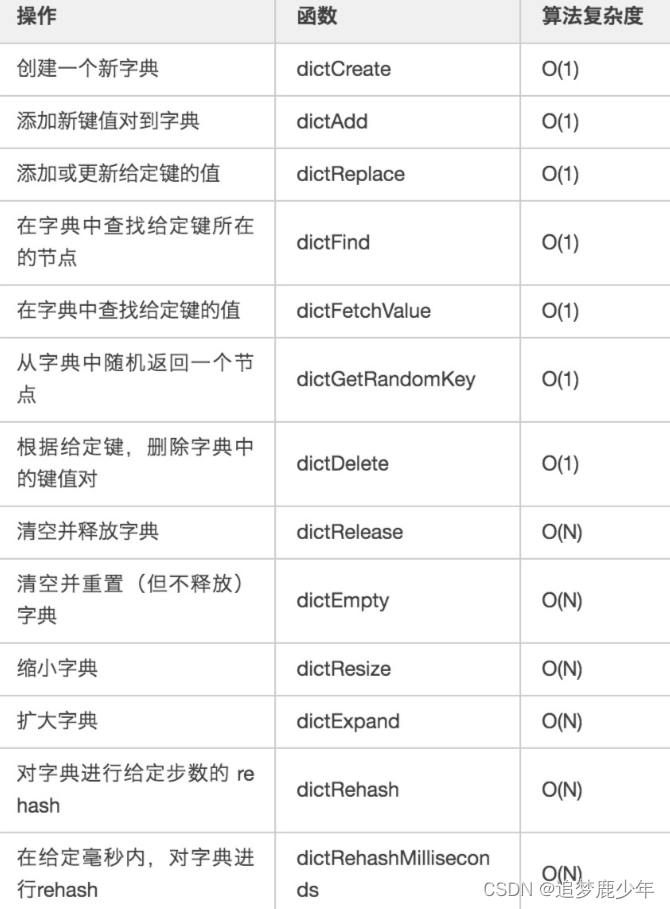
Redis第九讲 Redis之Hash数据结构Dict字典哈希算法与hash存储过程
Redis dict使用的哈希算法 前面提到,一个kv键值对,添加到哈希表时,需要用一个映射函数将key散列到一个具体的数组下标。 Redis 目前使用两种不同的哈希算法: MurmurHash2 是种32 bit 算法:这种算法的分布率和速度都非常好;Murmur哈希算法最大的特点是碰撞率低,计算速度…...
2个月月活突破1亿,增速碾压抖音,出道即封神的ChatGPT,现在怎么样了?ChatGPT它会干掉测试?
从互联网的普及到智能手机,都让广袤的世界触手而及,如今身在浪潮中的我们,已深知其力。 前阵子爆火的ChatGPT,不少人保持观望态度。现如今,国内关于ChatGPT的各大社群讨论,似乎沉寂了不少,现在…...

Linux常用文件目录操作指令
linux 文件目录操作指令pwd 指令ls 指令cd 指令mkdir 指令rmdir 指令touch 指令cp 指令rm 指令mv 指令cat 指令more 指令less 指令> 和 >> 指令echo 指令head 指令tail 指令ln 指令history 指令pwd 指令 基本语法 pwd (显示当前工作目录的绝对路径) ls 指令 基本语法…...
阿哈罗诺夫——玻姆效应(AB效应)
规范变换 规范场是与物理规律的定域规范变换不变性相联系的物质场纵场的旋度为零,横场的散度为零 由于 因此 为了消除此影响,我们需要对标势场做规范 库伦规范(Coulomb gauge):使麦克斯韦方程组自然满足静电场的条件 洛伦兹规范 (Lorentz gauge&#x…...

sed使用
概述 Linux sed 命令是利用脚本来处理文本文件。sed 可依照脚本的指令来处理、编辑文本文件。Sed 主要用来自动编辑一个或多个文件、简化对文件的反复操作、编写转换程序等。 语法 sed [-hnV][-e<script>][-f<script文件>][文本文件]注意:-e是可以省…...

redhat9忘记root密码操作(普通用户也适用)
目录 一.编辑启动条目 二、按enter键 三、重新挂载/sysroot,并且修改/sysroot的权限为rw 四、将根目录修改到/sysroot 五、修改密码 5.1修改root密码 5.2 修改普通用户的密码 六、创建文件 七、退出 八、测试 一.编辑启动条目 进入以下页面的时候࿰…...

Android 五种启动模式小结
ActivityRecord、TaskRecord、ActivityStack区别 ActivityRecord对应着一个Activity实例,保存了Activity所有相关信息 TaskRecord指的是一个任务栈,里面包含多个ActivityRecord ActivityStack用于管理TaskRecord 五种启动模式 Standard模式 默认的启…...

算法竞赛ICPC、CCPC、NIO、蓝桥杯、天梯赛
算法竞赛前言一、为什么学习算法竞赛二、学习算法的阶段三、算法竞赛具体学习内容1、基础数据结构1.1、链表1.1.1、动态链表1.1.2、静态链表1.1.3、STL list1.2、队列1.2.1、STL queue1.2.2、手写循环队列1.2.3、双端队列和单调队列1.2.4、优先队列1.3、栈1.3.1、STL stack1.3.…...

图像分割技术及经典实例分割网络Mask R-CNN(含基于Keras Python源码定义)
图像分割技术及经典实例分割网络Mask R-CNN(含Python源码定义) 文章目录图像分割技术及经典实例分割网络Mask R-CNN(含Python源码定义)1. 图像分割技术概述2. FCN与语义分割2.1 FCN简介2.2 反卷积2.2 FCN与语义分割的关系3. Mask …...
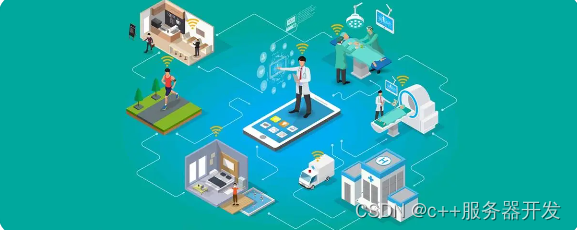
元宇宙和医疗保健
让我们明确定义医疗保健领域的元宇宙 元宇宙这个概念已经有几十年的存在历史了,尽管当Facebook改名为Meta时,这个话题才成了头版头条。现在卫生部门的领导们也开始关注这个话题。 数字卫生领域对元宇宙的定义是如今的医疗科技主要是由医疗软件解决方案…...

iOS_从相机或相册里扫描二维码或条形码
文章目录1. 从相机里扫描1.1 申请相机权限1.2 创建Scanner1.3 开始扫描1.4 处理扫描结果2. 从相册里扫描2.1 获取相册权限2.2 打开相册2.3 获得选择结果2.4 解析相片中的二维码或条形码1. 从相机里扫描 1.1 申请相机权限 导入: import AVFoundation在项目的 Info.…...
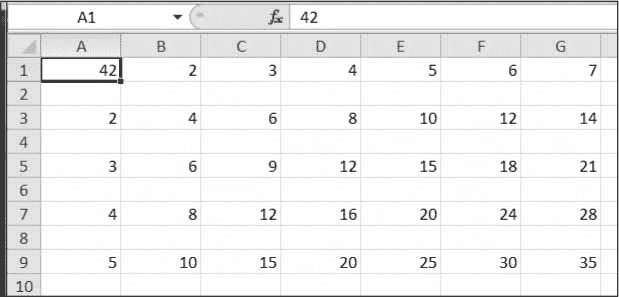
Python 自动化指南(繁琐工作自动化)第二版:十六、使用 CSV 文件和 JSON 数据
原文:https://automatetheboringstuff.com/2e/chapter16/ 在第 15 章,你学习了如何从 PDF 和 Word 文档中提取文本。这些文件是二进制格式的,需要特殊的 Python 模块来访问它们的数据。另一方面,CSV 和 JSON 文件只是纯文本文件。…...
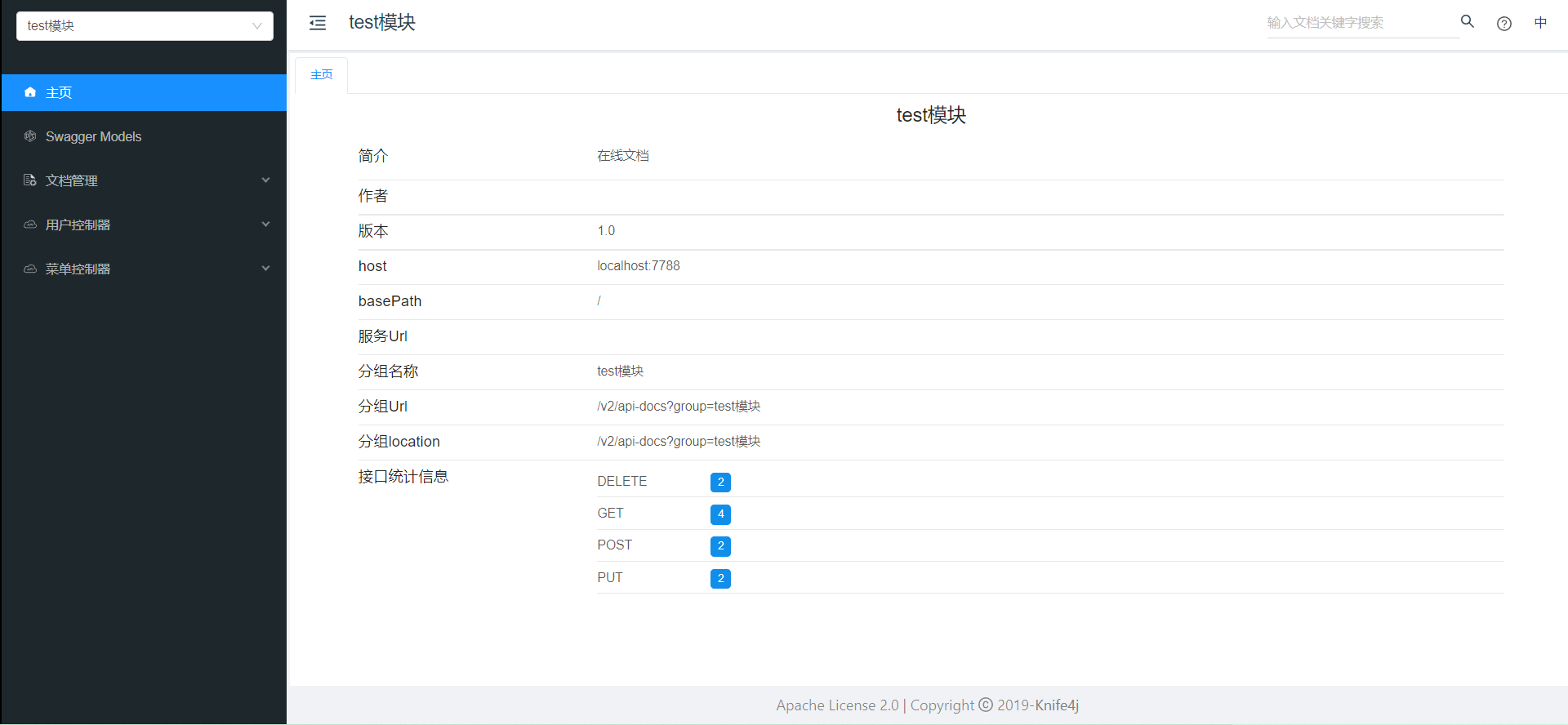
knife4j接口文档
knife4j是为Java MVC框架集成Swagger生成Api文档的增强解决方案,前身是swagger-bootstrap-ui,取名knife4j是希望它能像一把匕首一样小巧,轻量,并且功能强悍!其底层是对Springfox的封装,使用方式也和Springfox一致,只是对接口文档UI进行了优化。 核心功能…...
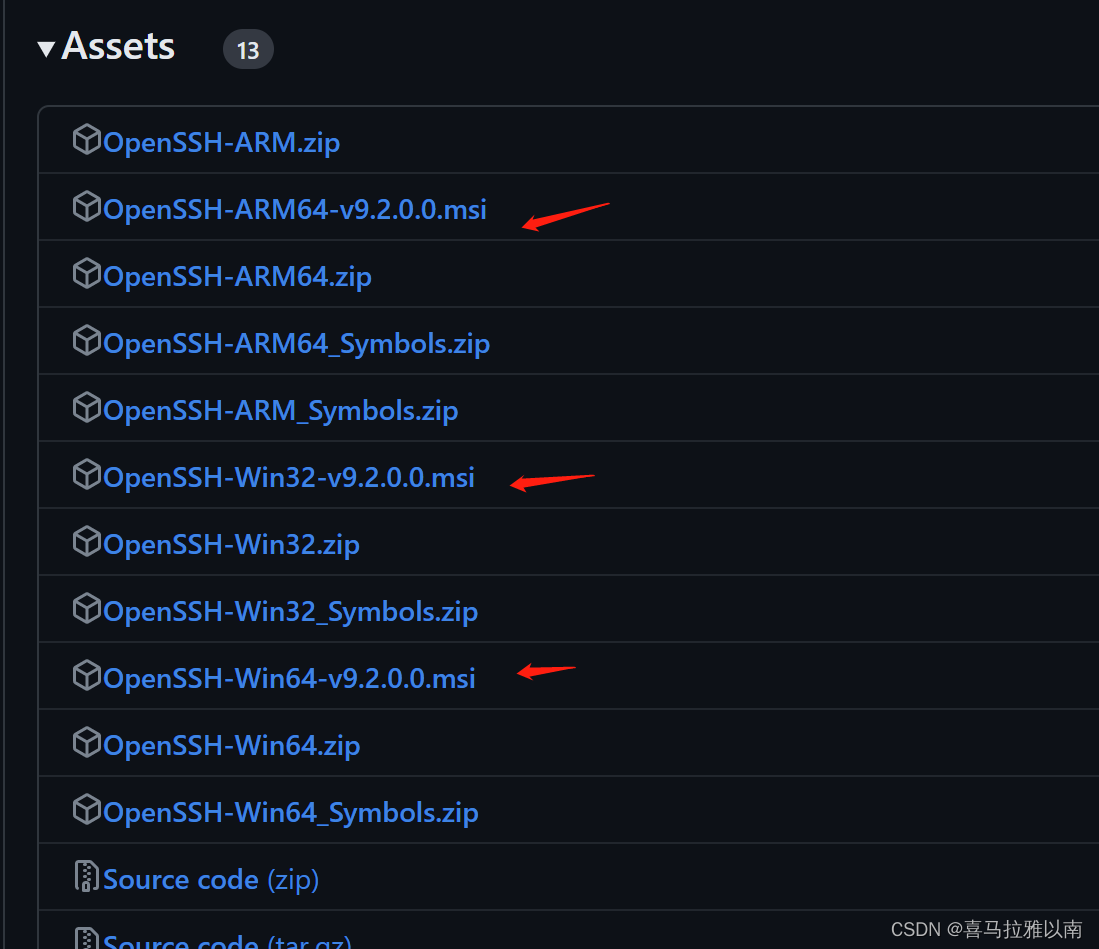
Windows机器安装SSH搭建,自己搞个局域网机房玩一玩
Windows机器安装SSH搭建为啥要装SSH安装OpenSSH使用 Windows 设置来安装 OpenSSHps脚本在线安装ps脚本离线安装其他二进制安装包安装为啥要装SSH 家里有多台Win机器,一台主机两个笔记本,本着不浪费的原则,打算把它们在平时的工作学习中利用起…...
二叉树的前序遍历(力扣144)
目录 题目描述: 解法一:递归法 解法二:迭代法 解法三:Morris 遍历 二叉树的前序遍历 题目描述: 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root […...
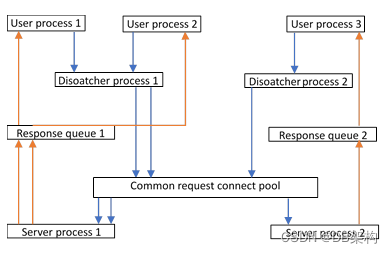
【数据库管理】①实例与数据库
1.Oracle RDBMS 架构图 2. Oracle 体系结构 由此区分database和instance的区别 No.1.oracle serverdatabase instance2.databasedata file、control file、redo log file3.instancean instance accesses a database4.oracle memorySGA PGA(oracle的内存结构)5.instanceSGA …...
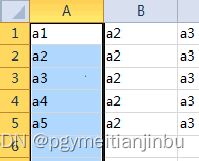
vba:单元格的选择,查找,合并,批注,SpecialCells,图形插入
一: 活动单元格:activecell,工作表中活动单元格只有一个 Sub activecells() a activecell.Address 取得活动单元格地址 Cells(2, 3).Activate 激活指定单元格 End Sub selection光标所选区域 Sub 光标所选区域() Selection 1 End Sub Sub …...
【内网安全】横向移动域控提权NetLogonADCSPACKDC永恒之蓝
文章目录章节点横向移动-系统漏洞-CVE-2017-0146(永恒之蓝)影响版本插件检测-横向移动CS联动MSF-检测&利用横向移动-域控提权-CVE-2014-6324横向移动-域控提权-CVE-2020-1472影响版本横向移动-域控提权-CVE-2021-42287前提条件影响版本python版本EXP利用过程C#版本EXP利用过…...
将本地项目上传到远程仓库的步骤
文章目录将本地项目上传到远程仓库的步骤1.进入想上传的项目文件夹2.初始化本地仓库3.添加该项目下的所有文件4.将文件添加到本地仓库中5.添加远程仓库6.将文件更新到远程仓库上7.将本地文件推送回到指定的远程仓库中将本地项目上传到远程仓库的步骤 1.进入想上传的项目文件夹…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
