《程序员面试金典(第6版)》面试题 08.09. 括号(回溯算法,特殊的排列问题,C++)
题目描述
括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。
说明:解集不能包含重复的子集。
例如,给出 n = 3,生成结果为:
["((()))","(()())","(())()","()(())","()()()"
]
解题思路与代码
这道题抽象总结出来,就只有两条规则,分别是:
- 左括号的数量不能多于n
- 右括号的数量不能多于左括号
方法一 : 回溯法
这道题我看了一下,比较适合用回溯法去解决。
-
我们需要一个辅助函数backtracking,它一共需要设置这么几个参数,分别是左括号的数量left,右括号的时候,right,n的大小n,存储结果集的向量result,一个string用来放括号字符str,共5个参数。
-
写一道回溯算法的题的时候,一般是先去想,这算法该如何返回。那么当str的长度等于2倍的n时,就该返回了,把str存入result后返回
-
之后我们就要去做判断了。这道题和一般的回溯算法不一样,我们这里不需要去使用for循环,直接进行条件判断就好了
-
如果左括号的数量小于n,我们就往str中加上一个左括号,然后进行回溯,回溯结束后,不要忘记删除加入str的括号。
-
如果右括号的数量小于左括号的数量,我们就往str中加入一个右括号,然后进行回溯,回溯结束后,别忘记加入str中的括号
整个回溯的逻辑就是这样,下面请看具体代码:
class Solution {
public:// 左括号的数量不能大于 n 。// 右括号的数量不能大于当前已经添加的左括号的数量。vector<string> generateParenthesis(int n) {vector<string> result;string str;backtracking(0,0,str,result,n);return result;}void backtracking(int left,int right,string& str,vector<string>& result,int n){if(str.size() == 2*n){result.push_back(str);return ;}if(left < n){str += "(";backtracking(left+1,right,str,result,n);str.pop_back();}if(left > right ){ str += ")";backtracking(left,right+1,str,result,n);str.pop_back();}}
};
复杂度分析
时间复杂度:
在这个问题中,我们需要生成所有可能的合法括号组合。对于每个位置,我们可以选择添加左括号或右括号(当然要满足条件)。因此,在最坏的情况下,时间复杂度可以看作是 O(2^(2n)/√n)。这个估计来自于卡特兰数(Catalan number),它是解决这类问题(括号生成)的通常方法。对于 n 对括号,卡特兰数 C(n) = (1/(n+1))(2n)!/((n!)(n+1)!))。卡特兰数增长的速度相当于 O(4^n/(n*√n))。
空间复杂度:
空间复杂度主要取决于两个方面:递归深度和结果列表。递归深度最多为 2n,因为每个递归调用都会消耗 O(1) 的栈空间,所以递归调用栈的空间复杂度为 O(2n)。结果列表中包含 C(n) 个元素,每个元素是一个长度为 2n 的字符串。因此,结果列表的空间复杂度为 O(C(n) * 2n) = O(4^n/√n * 2n)。
总结
这道题可以归类为回溯算法可以解决一类问题中的排列问题。但这和普通的排列问题还不一样,这是一种特殊的排列问题。因为左括号的数量要始终要大于右括号,有了限制条件后,就和一般的排列问题不一样了。
还是很有意思的,这一道题。这道题用回溯算法已经算是最优解了
这道题的解决方案与卡特兰数相关,它的时间复杂度和空间复杂度都与卡特兰数有关。
在这种情况下,尝试寻找一种更好的方法并不容易。因为我们需要生成所有可能的合法括号组合,所以无论如何,我们都需要遍历这个解空间。回溯算法在这里表现得非常好,因为它能够在满足约束条件的情况下生成所有可能的解。而且,它在遍历解空间时非常高效,因为它可以在不满足条件的情况下立即剪枝。
当然,这并不意味着没有其他方法可以解决这个问题。例如,你可以尝试动态规划,但这种方法的实现会更加复杂,而且在这种情况下它的性能可能不如回溯算法。所以,对于这道题,回溯方法已经是很好的解决方案了。
相关文章:

《程序员面试金典(第6版)》面试题 08.09. 括号(回溯算法,特殊的排列问题,C++)
题目描述 括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。 说明:解集不能包含重复的子集。 例如,给出 n 3,生成结果为: ["((()))","(()())…...
大厂面试篇--2023软件测试八股文最全文档,有它直接大杀四方
前言 已经到了金三银四的黄金招聘季节了,还在准备面试跳槽涨薪的小伙伴们可以看看本篇文章哟,这里呢笔者就不多说废话了直接上干货!答案已整理好,文末拿去即可!非常好用! 一、字节跳动测试面经篇 1、在搜…...

LeetCode326_326. 3 的幂
LeetCode326_326. 3 的幂 一、描述 给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。 整数 n 是 3 的幂次方需满足:存在整数 x 使得 n 3的x次方 示例 1: 输…...
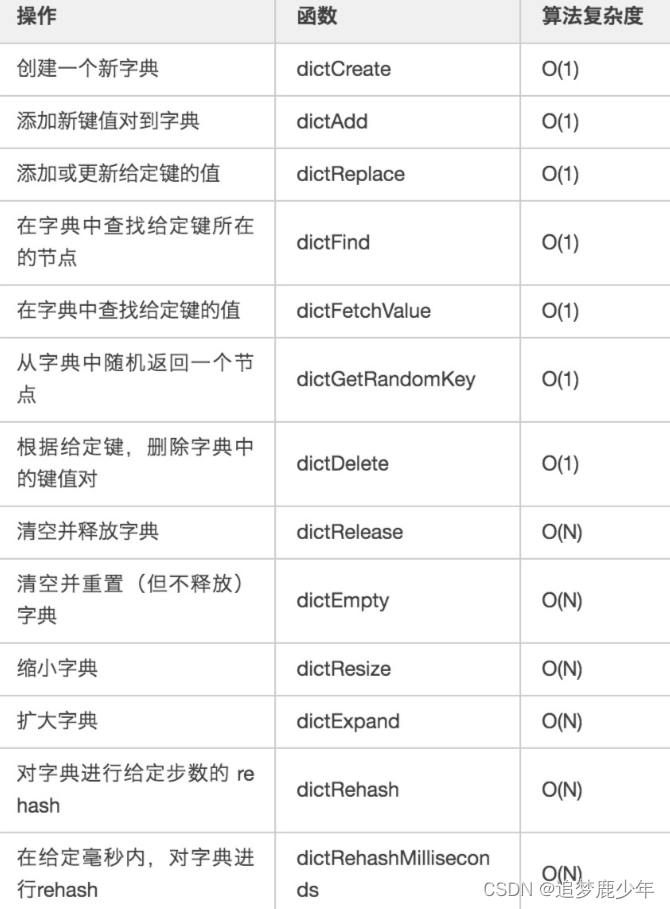
Redis第九讲 Redis之Hash数据结构Dict字典哈希算法与hash存储过程
Redis dict使用的哈希算法 前面提到,一个kv键值对,添加到哈希表时,需要用一个映射函数将key散列到一个具体的数组下标。 Redis 目前使用两种不同的哈希算法: MurmurHash2 是种32 bit 算法:这种算法的分布率和速度都非常好;Murmur哈希算法最大的特点是碰撞率低,计算速度…...
2个月月活突破1亿,增速碾压抖音,出道即封神的ChatGPT,现在怎么样了?ChatGPT它会干掉测试?
从互联网的普及到智能手机,都让广袤的世界触手而及,如今身在浪潮中的我们,已深知其力。 前阵子爆火的ChatGPT,不少人保持观望态度。现如今,国内关于ChatGPT的各大社群讨论,似乎沉寂了不少,现在…...

Linux常用文件目录操作指令
linux 文件目录操作指令pwd 指令ls 指令cd 指令mkdir 指令rmdir 指令touch 指令cp 指令rm 指令mv 指令cat 指令more 指令less 指令> 和 >> 指令echo 指令head 指令tail 指令ln 指令history 指令pwd 指令 基本语法 pwd (显示当前工作目录的绝对路径) ls 指令 基本语法…...
阿哈罗诺夫——玻姆效应(AB效应)
规范变换 规范场是与物理规律的定域规范变换不变性相联系的物质场纵场的旋度为零,横场的散度为零 由于 因此 为了消除此影响,我们需要对标势场做规范 库伦规范(Coulomb gauge):使麦克斯韦方程组自然满足静电场的条件 洛伦兹规范 (Lorentz gauge&#x…...

sed使用
概述 Linux sed 命令是利用脚本来处理文本文件。sed 可依照脚本的指令来处理、编辑文本文件。Sed 主要用来自动编辑一个或多个文件、简化对文件的反复操作、编写转换程序等。 语法 sed [-hnV][-e<script>][-f<script文件>][文本文件]注意:-e是可以省…...

redhat9忘记root密码操作(普通用户也适用)
目录 一.编辑启动条目 二、按enter键 三、重新挂载/sysroot,并且修改/sysroot的权限为rw 四、将根目录修改到/sysroot 五、修改密码 5.1修改root密码 5.2 修改普通用户的密码 六、创建文件 七、退出 八、测试 一.编辑启动条目 进入以下页面的时候࿰…...

Android 五种启动模式小结
ActivityRecord、TaskRecord、ActivityStack区别 ActivityRecord对应着一个Activity实例,保存了Activity所有相关信息 TaskRecord指的是一个任务栈,里面包含多个ActivityRecord ActivityStack用于管理TaskRecord 五种启动模式 Standard模式 默认的启…...

算法竞赛ICPC、CCPC、NIO、蓝桥杯、天梯赛
算法竞赛前言一、为什么学习算法竞赛二、学习算法的阶段三、算法竞赛具体学习内容1、基础数据结构1.1、链表1.1.1、动态链表1.1.2、静态链表1.1.3、STL list1.2、队列1.2.1、STL queue1.2.2、手写循环队列1.2.3、双端队列和单调队列1.2.4、优先队列1.3、栈1.3.1、STL stack1.3.…...

图像分割技术及经典实例分割网络Mask R-CNN(含基于Keras Python源码定义)
图像分割技术及经典实例分割网络Mask R-CNN(含Python源码定义) 文章目录图像分割技术及经典实例分割网络Mask R-CNN(含Python源码定义)1. 图像分割技术概述2. FCN与语义分割2.1 FCN简介2.2 反卷积2.2 FCN与语义分割的关系3. Mask …...
元宇宙和医疗保健
让我们明确定义医疗保健领域的元宇宙 元宇宙这个概念已经有几十年的存在历史了,尽管当Facebook改名为Meta时,这个话题才成了头版头条。现在卫生部门的领导们也开始关注这个话题。 数字卫生领域对元宇宙的定义是如今的医疗科技主要是由医疗软件解决方案…...

iOS_从相机或相册里扫描二维码或条形码
文章目录1. 从相机里扫描1.1 申请相机权限1.2 创建Scanner1.3 开始扫描1.4 处理扫描结果2. 从相册里扫描2.1 获取相册权限2.2 打开相册2.3 获得选择结果2.4 解析相片中的二维码或条形码1. 从相机里扫描 1.1 申请相机权限 导入: import AVFoundation在项目的 Info.…...
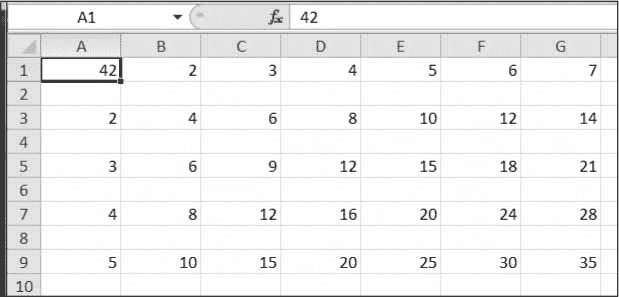
Python 自动化指南(繁琐工作自动化)第二版:十六、使用 CSV 文件和 JSON 数据
原文:https://automatetheboringstuff.com/2e/chapter16/ 在第 15 章,你学习了如何从 PDF 和 Word 文档中提取文本。这些文件是二进制格式的,需要特殊的 Python 模块来访问它们的数据。另一方面,CSV 和 JSON 文件只是纯文本文件。…...
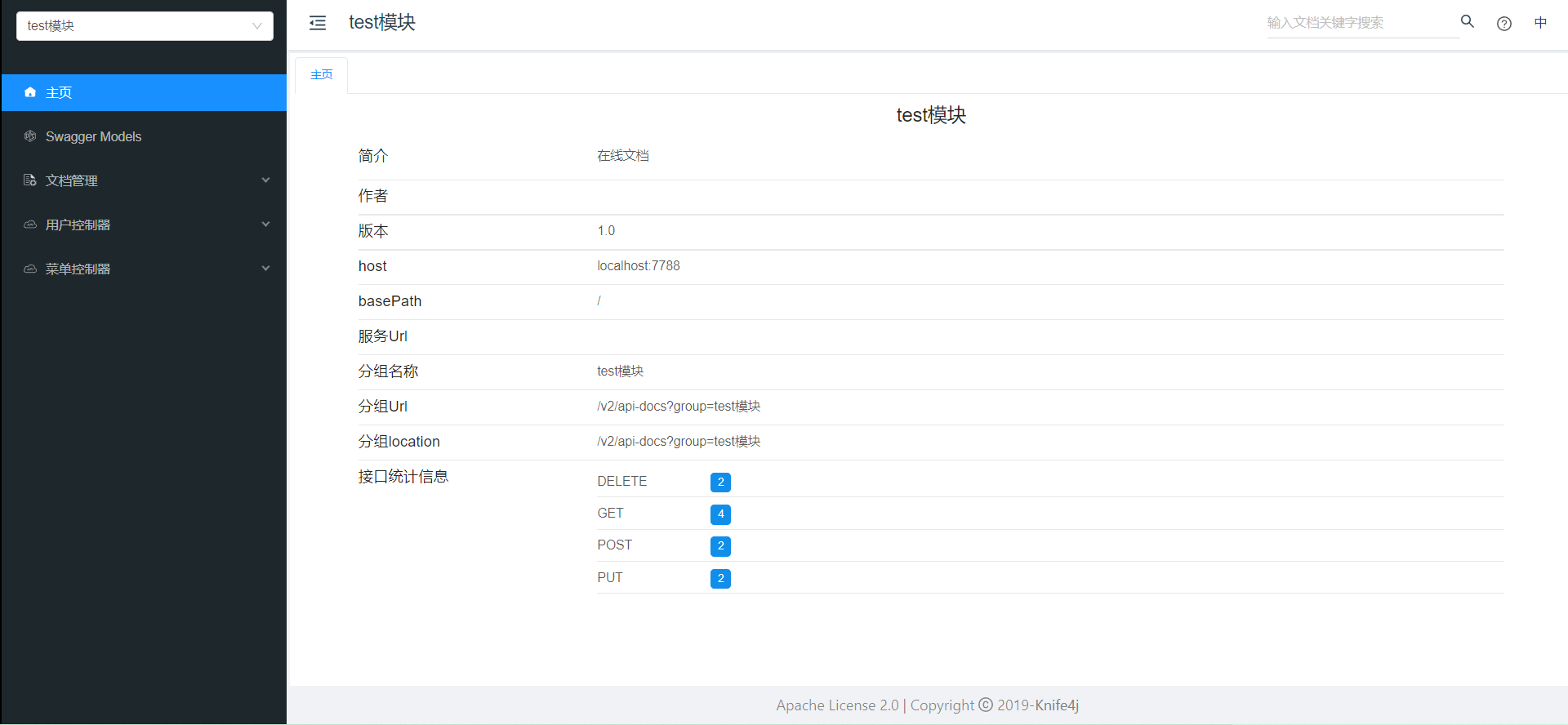
knife4j接口文档
knife4j是为Java MVC框架集成Swagger生成Api文档的增强解决方案,前身是swagger-bootstrap-ui,取名knife4j是希望它能像一把匕首一样小巧,轻量,并且功能强悍!其底层是对Springfox的封装,使用方式也和Springfox一致,只是对接口文档UI进行了优化。 核心功能…...
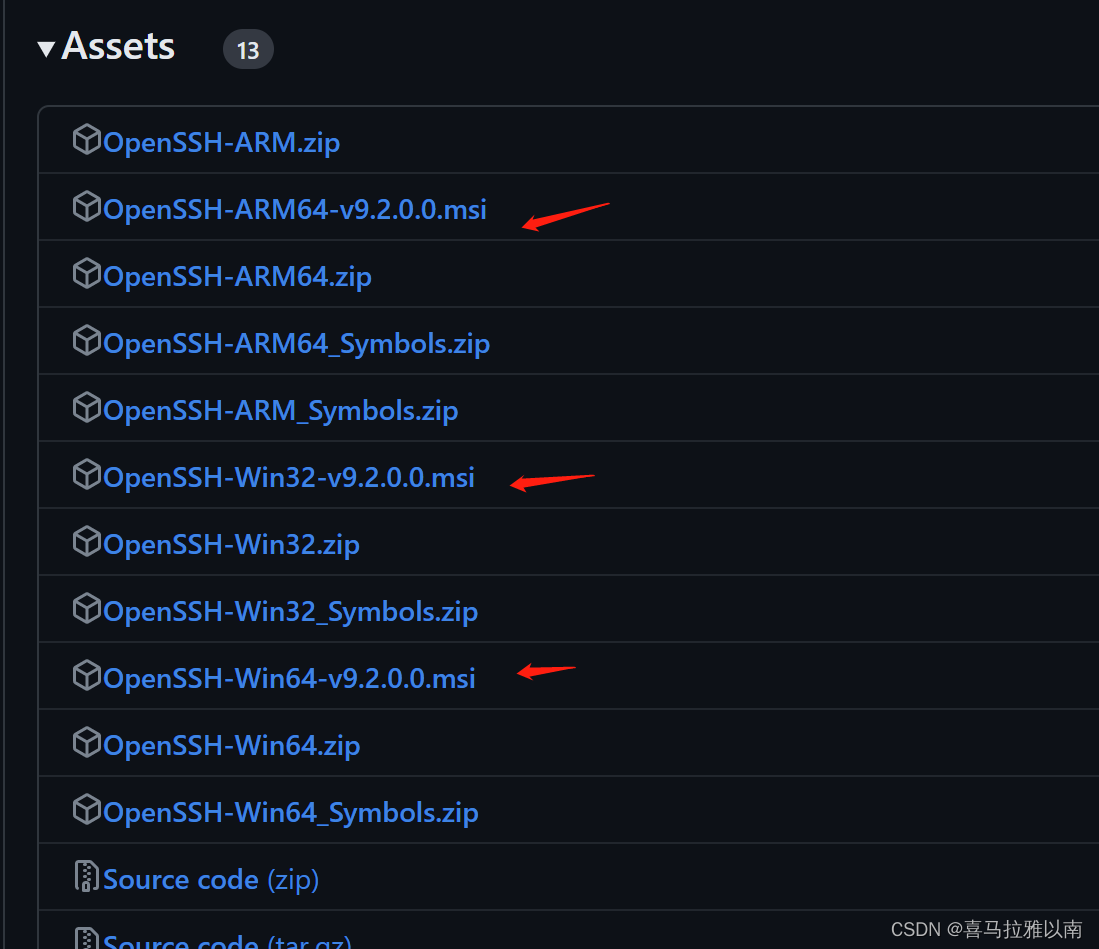
Windows机器安装SSH搭建,自己搞个局域网机房玩一玩
Windows机器安装SSH搭建为啥要装SSH安装OpenSSH使用 Windows 设置来安装 OpenSSHps脚本在线安装ps脚本离线安装其他二进制安装包安装为啥要装SSH 家里有多台Win机器,一台主机两个笔记本,本着不浪费的原则,打算把它们在平时的工作学习中利用起…...
二叉树的前序遍历(力扣144)
目录 题目描述: 解法一:递归法 解法二:迭代法 解法三:Morris 遍历 二叉树的前序遍历 题目描述: 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root […...
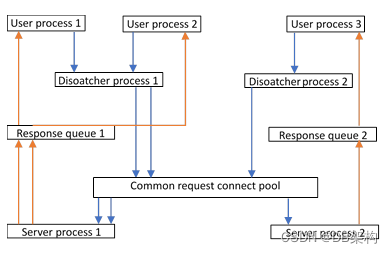
【数据库管理】①实例与数据库
1.Oracle RDBMS 架构图 2. Oracle 体系结构 由此区分database和instance的区别 No.1.oracle serverdatabase instance2.databasedata file、control file、redo log file3.instancean instance accesses a database4.oracle memorySGA PGA(oracle的内存结构)5.instanceSGA …...
vba:单元格的选择,查找,合并,批注,SpecialCells,图形插入
一: 活动单元格:activecell,工作表中活动单元格只有一个 Sub activecells() a activecell.Address 取得活动单元格地址 Cells(2, 3).Activate 激活指定单元格 End Sub selection光标所选区域 Sub 光标所选区域() Selection 1 End Sub Sub …...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
