数据结构之二叉搜索树(key模型与key_value模型)
二叉搜索树(key模型与key_value模型)
- 1. ⼆叉搜索树的概念
- 2. ⼆叉搜索树的性能分析
- 3. ⼆叉搜索树的插⼊
- 4. ⼆叉搜索树的查找
- 5. ⼆叉搜索树的删除
- 6. ⼆叉搜索树的实现代码
- 7. ⼆叉搜索树key和key/value使⽤场景
- 7.1 key搜索场景:
- 7.2 key/value搜索场景:
- 7.3 key/value⼆叉搜索树代码实现
- 8、运用于实际的key_value
今天我来介绍的是二叉搜索树,这一块我希望大家如果有不会的地方下来好好理解,这一节课与下一节的set/map关联挺大的。
1. ⼆叉搜索树的概念
⼆叉搜索树⼜称⼆叉排序树,它或者是⼀棵空树,或者是具有以下性质的⼆叉树:
–• 若它的左⼦树不为空,则左⼦树上所有结点的值都⼩于等于根结点的值
–• 若它的右⼦树不为空,则右⼦树上所有结点的值都⼤于等于根结点的值
–• 它的左右⼦树也分别为⼆叉搜索树
–• ⼆叉搜索树中可以⽀持插⼊相等的值,也可以不⽀持插⼊相等的值,具体看使⽤场景定义,后续我们学习map/set/multimap/multiset系列容器底层就是⼆叉搜索树,其中map/set不⽀持插⼊相等值,multimap/multiset⽀持插⼊相等值.(multimap/multiset)这一块我们下一节介绍,今天我主要介绍的是不允许冗余的情况

2. ⼆叉搜索树的性能分析
最优情况下,⼆叉搜索树为完全⼆叉树(或者接近完全⼆叉树),其⾼度为: O(log2 N)
最差情况下,⼆叉搜索树退化为单⽀树(或者类似单⽀),其⾼度为: O( N/2)
所以综合⽽⾔⼆叉搜索树增删查改时间复杂度为: O(N)
那么这样的效率显然是⽆法满⾜我们需求的,我们后续课程需要继续讲解⼆叉搜索树的变形,平衡⼆叉搜索树AVL树和红⿊树,才能适⽤于我们在内存中存储和搜索数据。
另外需要说明的是,⼆分查找也可以实现 O(logN) 级别的查找效率,但是⼆分查找有两⼤缺陷:
- 需要存储在⽀持下标随机访问的结构中,并且有序。
- 插⼊和删除数据效率很低,因为存储在下标随机访问的结构中,插⼊和删除数据⼀般需要挪动数据。
这⾥也就体现出了平衡⼆叉搜索树的价值。

3. ⼆叉搜索树的插⼊
以上的基本知识我们学习完后就来看一下二叉树的插入。
1、树为空,我们直接将第一个插入的节点作为根节点即可。
2、数不为空,按⼆叉搜索树性质,插⼊值⽐当前结点⼤往右⾛,插⼊值⽐当前结点⼩往左⾛,找到空位置,插⼊新结点。
3. 如果⽀持插⼊相等的值,插⼊值跟当前结点相等的值可以往右⾛,也可以往左⾛,找到空位置,插⼊新结点。(要注意的是要保持逻辑⼀致性,插⼊相等的值不要⼀会往右⾛,⼀会往左⾛)(这里我建议向左走,后序我们会学习平衡的概念,这棵树失衡的情况下,右节点会跑到左边)
这里我们可以按照之前学习二叉树时,二叉树的构建一样采用递归来插入,但这里有个简单的方式那就是循环,我们直接比较当前节点的值与插入的值的大小,如果小于就走左,大于就走右,等于直接就返回false(这里我只写不允许冗余,大家下来可以考虑有冗余的情况),如果当前节点走到空了,那这个位置就是我们需要插入的位置。
节点类:
template<class k>//k就是我们的key
struct BSTNode
{k _key;BSTNode<k>* _left;BSTNode<k>* _right;BSTNode(const k& x) :_key(x), _left(nullptr), _right(nullptr) {}//构造
};
//节点
插入部分:
bool insert(const k& x)
{if (_root == nullptr){_root = new Node(x);}//根节点为空Node* parent = nullptr;Node* cur = _root;while (cur){if (x < cur->_key){parent = cur;cur = cur->_left;}else if (x > cur->_key){parent = cur;cur = cur->_right;}elsereturn false;}//找到该插入的位置,为curcur = new Node(x);//找到以后还需要判断它插入在父节点哪一边if (x < parent->_key){parent->_left = cur;}else{parent->_right = cur;}return 0;
}
这里是需要引入cur(当前节点)的parent(父亲指针)的,因为我们要插入节点,需要将插入的节点与整棵树链接。
这一块写完不好测试对吧,因为调试窗口只能看到节点插入与否,那我们写一个中序遍历,首先搜索二叉树永远是一个左小于根,根小于右的结构,中序遍历一定是一个递增的数列,这一块要是不知道的建议去其他地方找视频看,文字不好演示,这里就不做演示了。
void _inorder(const Node* root)
{if (root == nullptr)return;_inorder(root->_left);cout << root->_key << ' ';_inorder(root->_right);}
这就是中序的代码,但是我们可以看到,要调用这个函数必须要传一个节点指针,二叉树的私有成员就是我们的_root指针,我们能在外部访问我们的根再传入吗?
为了不破坏类的封装,这里有两种方式解决:
1、getroot函数,提供访问根节点的指针。
2、再写一个共有的调用_inorder的函数,类外部不能访问,类内部是可以访问的。
void inorder()
{_inorder(_root);cout << endl;
}
这样就搞定了。
那现在我们来测试一下:

这里的key模型担任的工作是不是可以有去重加排序啊。
4. ⼆叉搜索树的查找
- 从根开始⽐较,查找x,x⽐根的值⼤则往右边⾛查找,x⽐根值⼩则往左边⾛查找。
- 最多查找⾼度次,⾛到到空,还没找到,这个值不存在。
- 如果不⽀持插⼊相等的值,找到x即可返回
- 如果⽀持插⼊相等的值,意味着有多个x存在,⼀般要求查找中序的第⼀个x。如下图,查找3,要找到1的右孩⼦的那个3返回

写完插入写查找是不是就太简单了啊
Node* find(const k& x)
{Node* cur = _root;while (cur){if (x < cur->_key)cur = cur->_left;else if (x > cur->_key)cur = cur->_right;elsereturn cur;}return nullptr;
}
这里我们就不需要parent了,因为我们只是查找当前节点在不在,跟父节点没有半毛钱关系对吧。
5. ⼆叉搜索树的删除
⾸先查找元素是否在⼆叉搜索树中,如果不存在,则返回false。
如果查找元素存在则分以下四种情况分别处理:(假设要删除的结点为N)
- 要删除结点N左右孩⼦均为空
- 要删除的结点N左孩⼦位空,右孩⼦结点不为空
- 要删除的结点N右孩⼦位空,左孩⼦结点不为空
- 要删除的结点N左右孩⼦结点均不为空
对应以上四种情况的解决⽅案:
5. 把N结点的⽗亲对应孩⼦指针指向空,直接删除N结点(情况1可以当成2或者3处理,效果是⼀样的)
6. 把N结点的⽗亲对应孩⼦指针指向N的右孩⼦,直接删除N结点
7. 把N结点的⽗亲对应孩⼦指针指向N的左孩⼦,直接删除N结点
8. ⽆法直接删除N结点,因为N的两个孩⼦⽆处安放,只能⽤替换法删除。找N左⼦树的值最⼤结点R(最右结点)或者N右⼦树的值最⼩结点R(最左结点)替代N,因为这两个结点中任意⼀个,放到N的位置,都满⾜⼆叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换,转⽽变成删除R结点,R结点符合情况2或情况3,可以直接删除。

这是第一种与第二种情况。
第三种情况较为复杂一点:

bool erase(const k& x)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (x < cur->_key){parent = cur;cur = cur->_left;}else if (x > cur->_key){parent = cur;cur = cur->_right;}else//找到当前位置{if (cur->_left == nullptr)//左为空{if (_root == cur)//特殊情况,当cur为空,且左为空,就将根移动{_root = cur->_right;}else{if (cur == parent->_left)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr)//右为空{if (_root == cur)//同上{_root = cur->_left;}else{if (cur == parent->_left)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else//双边节点{Node* replaceparent = cur;Node* replace = cur->_right;while (replace->_left){replaceparent = replace;replace = replace->_left;}cur->_key = replace->_key;//replace的左边一定没有节点了if (replace == replaceparent->_left)replaceparent->_left = replace;elsereplaceparent->_right = replace;delete replace;}return true;}}return false;
}
6. ⼆叉搜索树的实现代码
#include<iostream>
using namespace std;namespace key
{template<class k>struct BSTNode{k _key;BSTNode<k>* _left;BSTNode<k>* _right;BSTNode(const k& x) :_key(x), _left(nullptr), _right(nullptr) {}};//节点template<class k>class BSTree{typedef BSTNode<k> Node;public:BSTree() = default;//强制生成构造BSTree(const BSTree& t){_root = copy(t._root);}//拷贝构造,这块比较简单,如果实在不懂的话私聊我BSTree& operator=(BSTree t){swap(_root, t._root);return *this;}//赋值构造~BSTree(){destroy(_root);_root = nullptr;}//析构采用一个后序遍历即可bool insert(const k& x){if (_root == nullptr){_root = new Node(x);}//根节点为空Node* parent = nullptr;Node* cur = _root;while (cur){if (x < cur->_key){parent = cur;cur = cur->_left;}else if (x > cur->_key){parent = cur;cur = cur->_right;}elsereturn false;}//找到该插入的位置,为curcur = new Node(x);if (x < parent->_key){parent->_left = cur;}else{parent->_right = cur;}return 0;}void inorder(){_inorder(_root);cout << endl;}bool erase(const k& x){Node* parent = nullptr;Node* cur = _root;while (cur){if (x < cur->_key){parent = cur;cur = cur->_left;}else if (x > cur->_key){parent = cur;cur = cur->_right;}else//找到当前位置{if (cur->_left == nullptr){if (_root == cur){_root = cur->_right;}else{if (cur == parent->_left)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr){if (_root == cur){_root = cur->_left;}else{if (cur == parent->_left)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else//双边节点{Node* replaceparent = cur;Node* replace = cur->_right;while (replace->_left){replaceparent = replace;replace = replace->_left;}cur->_key = replace->_key;//replace的左边一定没有节点了if (replace == replaceparent->_left)replaceparent->_left = replace;elsereplaceparent->_right = replace;delete replace;}return true;}}return false;}Node* find(const k& x){Node* cur = _root;while (cur){if (x < cur->_key)cur = cur->_left;else if (x > cur->_key)cur = cur->_right;elsereturn cur;}return nullptr;}private:void _inorder(const Node* root){if (root == nullptr)return;_inorder(root->_left);cout << root->_key << ' ';_inorder(root->_right);}void destroy(Node* root){if (root == nullptr)return;destroy(root->_left);destroy(root->_right);delete root;}Node* copy(Node* root){if (root == nullptr)return nullptr;Node* r = new Node(root->_key);r->_left = copy(root->_left);r->_right = copy(root->_right);return r;}Node* _root = nullptr;};
}
这份代码是key的模型,什么是key_value呢?就是每个节点存储两个值,key跟上面写的一样作为插入删除等等的基准,value想存啥就存啥。
7. ⼆叉搜索树key和key/value使⽤场景
7.1 key搜索场景:
只有key作为关键码,结构中只需要存储key即可,关键码即为需要搜索到的值,搜索场景只需要判断key在不在。key的搜索场景实现的⼆叉树搜索树⽀持增删查,但是不⽀持修改,修改key破坏搜索树结构了。
场景1:⼩区⽆⼈值守⻋库,⼩区⻋库买了⻋位的业主⻋才能进⼩区,那么物业会把买了⻋位的业主的⻋牌号录⼊后台系统,⻋辆进⼊时扫描⻋牌在不在系统中,在则抬杆,不在则提⽰⾮本⼩区⻋辆,⽆法进⼊。
场景2:检查⼀篇英⽂⽂章单词拼写是否正确,将词库中所有单词放⼊⼆叉搜索树,读取⽂章中的单词,查找是否在⼆叉搜索树中,不在则波浪线标红提⽰。
7.2 key/value搜索场景:
每⼀个关键码key,都有与之对应的值value,value可以任意类型对象。树的结构中(结点)除了需要存储key还要存储对应的value,增/删/查还是以key为关键字⾛⼆叉搜索树的规则进⾏⽐较,可以快速查找到key对应的value。key/value的搜索场景实现的⼆叉树搜索树⽀持修改,但是不⽀持修改key,修改key破坏搜索树结构了,可以修改value。
场景1:简单中英互译字典,树的结构中(结点)存储key(英⽂)和vlaue(中⽂),搜索时输⼊英⽂,则同时查找到了英⽂对应的中⽂。
场景2:商场⽆⼈值守⻋库,⼊⼝进场时扫描⻋牌,记录⻋牌和⼊场时间,出⼝离场时,扫描⻋牌,查找⼊场时间,⽤当前时间-⼊场时间计算出停⻋时⻓,计算出停⻋费⽤,缴费后抬杆,⻋辆离场。
场景3:统计⼀篇⽂章中单词出现的次数,读取⼀个单词,查找单词是否存在,不存在这个说明第⼀次出现,(单词,1),单词存在,则++单词对应的次数。
7.3 key/value⼆叉搜索树代码实现
这里只需要增加一个模版参数即可
namespace key_value
{template<class k,class v>struct BSTNode{k _key;v _value;BSTNode<k,v>* _left;BSTNode<k,v>* _right;BSTNode(const k& x,const v& y) :_key(x), _value(y), _left(nullptr), _right(nullptr) {}};//节点template<class k,class v>class BSTree{typedef BSTNode<k,v> Node;public:BSTree() = default;//强制生成构造BSTree(const BSTree& t){_root = copy(t._root);}BSTree& operator=(BSTree t){swap(_root, t._root);return *this;}~BSTree(){destroy(_root);_root = nullptr;}bool insert(const k& x,const v& y){if (_root == nullptr){_root = new Node(x, y);}//根节点为空Node* parent = nullptr;Node* cur = _root;while (cur){if (x < cur->_key){parent = cur;cur = cur->_left;}else if (x > cur->_key){parent = cur;cur = cur->_right;}elsereturn false;}//找到该插入的位置,为curcur = new Node(x,y);if (x < parent->_key){parent->_left = cur;}else{parent->_right = cur;}return 0;}void inorder(){_inorder(_root);cout << endl;}bool erase(const k& x){Node* parent = nullptr;Node* cur = _root;while (cur){if (x < cur->_key){parent = cur;cur = cur->_left;}else if (x > cur->_key){parent = cur;cur = cur->_right;}else//找到当前位置{if (cur->_left == nullptr){if (_root == cur){_root = cur->_right;}else{if (cur == parent->_left)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}else if (cur->_right == nullptr){if (_root == cur){_root = cur->_left;}else{if (cur == parent->_left)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else//双边节点{Node* replaceparent = cur;Node* replace = cur->_right;while (replace->_left){replaceparent = replace;replace = replace->_left;}cur->_key = replace->_key;//replace的左边一定没有节点了if (replace == replaceparent->_left)replaceparent->_left = replace;elsereplaceparent->_right = replace;delete replace;}return true;}}return false;}Node* find(const k& x){Node* cur = _root;while (cur){if (x < cur->_key)cur = cur->_left;else if (x > cur->_key)cur = cur->_right;elsereturn cur;}return nullptr;}private:void _inorder(const Node* root){if (root == nullptr)return;_inorder(root->_left);cout << root->_key << "->" << root->_value << endl;_inorder(root->_right);}void destroy(Node* root){if (root == nullptr)return;destroy(root->_left);destroy(root->_right);delete root;}Node* copy(Node* root){if (root == nullptr)return nullptr;Node* r = new Node(root->_key,root->_value);r->_left = copy(root->_left);r->_right = copy(root->_right);return r;}Node* _root = nullptr;};
}
8、运用于实际的key_value
void test4()
{string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };key_value::BSTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在,说明水果第一次出现,则插入<水果, 1>// 2、在,则查找到的结点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.find(str);if (ret == nullptr){countTree.insert(str, 1);}else{// 修改valueret->_value++;}}countTree.inorder();key_value::BSTree<string, int> copy = countTree;copy.inorder();}

相关文章:

数据结构之二叉搜索树(key模型与key_value模型)
二叉搜索树(key模型与key_value模型) 1. ⼆叉搜索树的概念2. ⼆叉搜索树的性能分析3. ⼆叉搜索树的插⼊4. ⼆叉搜索树的查找5. ⼆叉搜索树的删除6. ⼆叉搜索树的实现代码7. ⼆叉搜索树key和key/value使⽤场景7.1 key搜索场景:7.2 key/value搜…...

图说几何学2300年重大错误:附着在直线z上的直线段必是z的一部分
黄小宁 用泡沫塑料和油漆制成的铅球与真正的铅球,两者有不同的内部形状。同样,数学有长度相同但内部形状不同的伪≌直线段。 几何学有史2300年来一直认定附着在直线z上的直线段一定是z的一部分。其实这是2300年肉眼直观错觉——百年病态集论的症结。 …...
技术分析)
汽车网关(GW)技术分析
一、引言 在现代汽车电子系统中,汽车网关(Gateway,简称 GW)扮演着至关重要的角色。随着汽车电子技术的不断发展,汽车内部的电子控制单元(Electronic Control Unit,简称 ECU)数量不断…...

Telnet命令详解:安装、用法及应用场景解析
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storm…...
)
C++之LIST模拟实现(代码纯享版)
目录 文章目录 前言 一、代码 总结 前言 本文主要展示了模拟List的代码实现 一、代码 #pragma once #include<iostream> #include<assert.h> using namespace std; namespace zlh {template<class T>struct list_node{T _data;list_node<T>* _next;l…...

华为OD机试 - 括号匹配 - 栈(Python/JS/C/C++ 2024 E卷 100分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试真题(Python/JS/C/C)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,…...

打破欧美10年芯片垄断,杨振宁教授关门弟子,仅用三年创造奇迹
有这么一位超级厉害的中国人,硬是把欧美那边垄断了十年的芯片技术给“撬”开了!说起来,这才是我们该追的真正明星啊!那么,这位大神到底是谁?又是怎么让欧美芯片圈儿里的人听到她的名字就心里发怵的呢&#…...
视频写入类VideoWriter之用于将图像帧写入视频文件函数write()的使用)
OpenCV视频I/O(20)视频写入类VideoWriter之用于将图像帧写入视频文件函数write()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 cv::VideoWriter::write() 函数用于将图像帧写入视频文件。 该函数/方法将指定的图像写入视频文件。图像的大小必须与打开视频编写器时指定的大…...
——FFmpeg源码中,解码Script Tag的实现)
音视频入门基础:FLV专题(14)——FFmpeg源码中,解码Script Tag的实现
一、引言 在《音视频入门基础:FLV专题(9)——Script Tag简介》中对Script Tag进行了简介,本文讲述FFmpeg源码中是怎样解码FLV文件的Script Tag,拿到里面的信息。 二、flv_read_packet函数 从《音视频入门基础&#x…...

小猿口算APP脚本(协议版)
小猿口算是一款专注于数学学习的教育应用,主要面向小学阶段的学生。它提供多种数学练习和测试,包括口算、速算、应用题等。通过智能化的题目生成和实时批改功能,帮助学生提高数学计算能力。此外,它还提供详细的学习报告和分析,帮助家长和教师了解学生的学习进度和薄弱环节…...

【长文梳理webserver核心】核心类篇
前言 有三个核心组件支撑一个reactor实现 [持续] 的 [监听] 一组fd,并根据每个fd上发生的事件 [调用] 相应的处理函数。这三个组件就是 EventLoop 、Channel 以及 Poller 三个类,其中 EventLoop 可以看作是对业务线程的封装,而 Channel 可以看…...

[实用工具]Docker安装nextcloud实现私有云服务和onlyoffice
Nextcloud是一款开源的云存储和协作平台,允许用户在自己的服务器上存储和访问文件,同时提供强大的协作工具。它可以替代商业云存储服务,让用户拥有完全控制和自主管理自己的数据。 Nextcloud支持文件上传和下载,可以通过Web界面、…...
(240))
基于STM32设计的生猪健康检测管理系统(NBIOT+OneNet)(240)
文章目录 一、前言1.1 项目介绍【1】项目开发背景【2】设计实现的功能【3】项目硬件模块组成1.2 设计思路1.3 项目开发背景【1】选题的意义【2】可行性分析【3】参考文献【4】项目背景【5】摘要1.4 开发工具的选择【1】设备端开发【2】上位机开发1.5 系统功能总结1.6 系统框架图…...

springboot kafka多数据源,通过配置动态加载发送者和消费者
前言 最近做项目,需要支持kafka多数据源,实际上我们也可以通过代码固定写死多套kafka集群逻辑,但是如果需要不修改代码扩展呢,因为kafka本身不处理额外逻辑,只是起到削峰,和数据的传递,那么就需…...

【华为】基于华为交换机的VLAN配置与不同VLAN间通信实现
划分VLAN(虚拟局域网)主要作用: 一、提高网络安全性 广播域隔离访问控制增强 二、优化网络性能 减少网络拥塞提高网络可管理性 sysytem-view #进入系统视图配置参数 vlan batch 10 20 #批量创建vlan LSW3: int g0/0/1 port…...

力扣题11~20
题11(中等): 思路: 这种题目第一眼就是双循环,但是肯定不行滴,o(n^2)这种肯定超时,很难接受。 所以要另辟蹊径,我们先用俩指针(标志位)在最左端和最右端&am…...
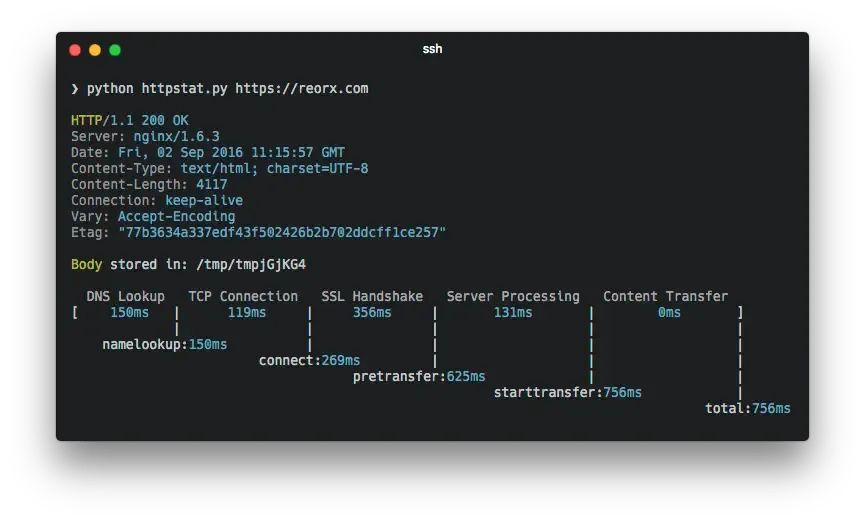
更美观的HTTP性能监测工具:httpstat
reorx/httpstat是一个旨在提供更美观和详细HTTP请求统计信息的cURL命令行工具,它能够帮助开发者和运维人员深入理解HTTP请求的性能和状态。 1. 基本概述 项目地址:https://github.com/reorx/httpstat语言:该工具主要是以Python编写ÿ…...

在2024 VDC,听一曲“蓝心智能”的江河协奏
作为科技从业者,我们每年参加的终端产品发布会和开发者大会,少则几十场。说每一场都别有新意,那自然是不可能的,但每次去vivo的活动现场,总能给我耳目一新的感觉。 雨果说过,音乐可以表达难以用语言描述&am…...
算法来优化掩模设计)
Python编写的数字光刻仿真程序,使用了Hopkins光刻模型和粒子群优化(PSO)算法来优化掩模设计
Python编写的数字光刻仿真程序,使用了Hopkins光刻模型和粒子群优化(PSO)算法来优化掩模设计,以减少光刻过程中的图形偏差。 4. 定义了几个函数来模拟光波通过光刻系统的变化: - `transfer_function`:计算光波的相位变化。 - `light_source_function`:描述光源在各…...
)
【AD那些事 11】绘制PCB板时“隔离” 的那些事(笔记摘抄)
在设计新板子时发现需要考虑隔离!!!!!!!!!!!于是我在网上找了很多资料,摘抄了一些,整理了一下,作为笔记&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
