JAVA-数据结构-排序
1.直接插入排序
1.原理:和玩扑克牌一样,从左边第二个牌开始,选中这个,和前面的所有牌比较,插在合适的位置

public static void insertsort(int[] arr){//直接插入排序for (int i = 1; i < arr.length; i++) {//此循环用来从1开始确定牌的位置int j = i-1;//得到j前面一个元素int tmp = arr[i];//将i处元素取出来,用来作比较for (; j >=0 ; j--) {//此循环用来和i前面的比较,将i放在正确的位置if(arr[j] > tmp){arr[j+1] = arr[j];//若i前面的比i大则将前面的值赋值给后面}else{
// arr[j+1] = tmp;break;//比前面都要大,没有比较的必要}}arr[j+1] = tmp;//j走完上面循环为-1,上面走完一次循环j=0时为空,}}直接插入排序特点
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
2.希尔排序
希尔排序是直接插入排序的Promax版本,将直接插入排序分为n份,比较完n份,排序即成功
思想:先选定一个整数,把待排序文件中所有记录分成多个组,
所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达
=1时,所有记录在统一组内排好序。
public static void shellSort(int[] array){//希尔排序是直接插入排序的优化int gap = array.length;while(gap > 0){//将每组距离最终干为1,即可成功gap /= 2;//得到每组的距离shell(array,gap);}}public static void shell(int[] array,int gap){for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j--) {if(array[j] > tmp){array[j+gap] = array[j];}else{array[j+gap] = tmp;break;}}array[j+gap] = tmp;}}3.选择排序
基本思想:一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元
素排完 。
public static void selsctSort1(int[] array){//选择排序基础版for (int i = 0; i < array.length; i++) {int minIndex = i;//每循环一次确定一个从左往右的最小值int j = i+1;for (; j <array.length; j++) {if(array[minIndex] > array[j]){minIndex = j;//将minTndex和j的下标先进行交换,找到最小的和其交换}//从一次次循环中得出在[i,length)的最小值}swap(array,minIndex,i);}}public static void selsctSort(int[] array){//选择排序promax版int left = 0;int right = array.length-1;while (left < right){int minIndex = left;int maxIndex = left;//统一从没排序的起点开始for (int i = left+1; i < array.length; i++) {if(array[maxIndex] < array[i]){maxIndex = i;}if(array[minIndex] > array[i]){minIndex = i;}}swap(array,left,minIndex);swap(array,right,maxIndex);left++;right--;}}public static void swap(int[]array ,int minIndex,int j){int tmp = array[j];array[j] = array[minIndex];array[minIndex] = tmp;}
}总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
4. 堆排序
降序建大堆,升序建小堆
详情思路请看之前写的堆部分
https://mp.csdn.net/mp_blog/creation/editor/139502440
/*** 堆排序* 时间复杂度:O(n*logN)* 空间复杂度:O(1)* 稳定性:不稳定* @param array*/public static void heapSort(int[] array) {createHeap(array);int end = array.length-1;while (end > 0) {swap(array,0,end);siftDown(array,0,end);end--;}}private static void createHeap(int[] array) {for (int parent = (array.length-1-1)/2; parent >= 0; parent--) {siftDown(array,parent,array.length);}}/**** @param array* @param parent 每棵子树调整的根节点* @param length 每棵子树调整的结束节点*/private static void siftDown(int[] array, int parent, int length) {int child = 2 * parent + 1;while (child < length) {if(child + 1 < length && array[child] < array[child+1]) {child++;}if(array[child] > array[parent]) {swap(array, parent, child);parent = child;child = 2*parent+1;}else {break;}}}6.快速排序
思想:任取待排序元素序列中的某元
素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有
元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
翻译过来实现过程就是取第一个数,分别在头和尾定义一个指针 ,头指针找比第一个数大的(需求就是把小的放在左边所以需要找大的和右边大的交换),尾指针找比第一个小的,两个都找到后,进行交换,确保左边的都是小于或等于第一个数的,右边都是大于或等于第一个数的,直到两个指针位置相等,然后再交换第一个与它们的位置,通过递归将它们分为一个个更小的然后即可完成
快速排序Hoare法实现过程
问题:为什么先从后面开始
如果先从前面开始则会造成最后汇合点大于key.
递归法
通过left和right的不断变化,直到left与right相遇为止,当不断分为很多的left和right后,
public class Sort {public static void swap(int[]array ,int minIndex,int j){int tmp = array[j];array[j] = array[minIndex];array[minIndex] = tmp;}public static void qsort(int[] array){int left = 0,right = array.length-1;parttrtions(array,left,right);}private static void parttrtions(int[]array,int left,int right){if(left>=right){return;}int start = parttrtion(array,left,right);parttrtions(array,left,start-1);parttrtions(array,start+1,right);}private static int parttrtion(int[] array,int left,int right){//Hoare版int privt = array[left];int end = right,start = left;while(start<end){while(start<end&& array[end] >= privt) {//从右往左直到找到比array[start](privt)小的放在end--;}while(start<end&&array[start] <= privt){//跳出小循环说明找到了比privt大的数start++;}swap(array,left,start);}return start;}private static int parttrtion1(int[] array,int left,int right){//挖坑法int privt = array[left];int end = right,start = left;while(start<end){while(start<end&& array[end] >= privt) {//从右往左直到找到比array[start](privt)小的放在end--;}array[start] = array[end];//将end下标的值来补充start的空缺while(start<end&&array[start] <= privt){//跳出小循环说明找到了比privt大的数start++;}array[end] = privt;//将start下标的值来补充end的空缺}return start;}
}
快排的优化:
1.三数取中法:如果是单一的数则可能造成,单支树的产生,最高造成N(O*2),所以可以提前将中间的值给到start,这样能极大减少计算量
private static int getMiddleNum(int[] array,int left,int right) {int mid = (left+right)/2;if(array[left] < array[right]) {if(array[mid] < array[left]) {return left;}else if(array[mid] > array[right]) {return right;}else {return mid;}}else {if(array[mid] > array[left]) {return left;}else if(array[mid] < array[right]) {return right;}else {return mid;}}}非递归法
利用栈后进先出不断变化left和right的值
public static void qsort1(int[] array){int left = 0,right = array.length-1;int par = parttrtion(array,left,right);Stack<Integer> stack = new Stack<>();if(par>left+1){stack.push(left);stack.push(par-1);}if(par < right-1){stack.push(par+1);stack.push(right);}while(!stack.empty()){right = stack.pop();left = stack.pop();par = parttrtion(array,left,right);if(par>left+1){stack.push(left);stack.push(par-1);}if(par < right-1){stack.push(par+1);stack.push(right);}}}
总结:
1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(logN)
4. 稳定性:不稳定
7.归并排序
思想:先将数组分成很多小份,然后再进行排序,然后把排序完的数组重新整和,最终得到一个有序数组。
递归法
1.首先将大数组分为小数组,把大问题拆分为小问题,1.找到最底层的两个数组,2.排序
public void mergeSortTmp(int[]a,int left,int right){//将数组先分开再合并if(left>=right){return;}int mid = (left+right)/2;mergeSortTmp(a,left,mid);//分成很多份,找到最左边mergeSortTmp(a,mid+1,right);//上层递归完成,找到对应要排序的另一个数组merge(a,mid,left,right);//两个都找到后,进行排序操作}2.然后利用两个数组组合排序的方法,定义两个指针,取到小的添加到新的数组
private void merge(int[]a,int mid,int left,int right){int [] array = new int[right-left+1];int set = 0;int s1 = left;int e1 = mid;int s2 = mid+1;int e2 = right;while(s1<e1&&s2<e2){if(a[s1] < a[s2]){array[set++] = a[s1++];}else {array[set++] = a[s2++];}}while (s1 <= mid) {array[set++] = array[s1++];}while (s2 <= right) {array[set++] = array[s2++];}for (int i = 0; i < array.length; i++) {a[i+left] = array[i];//分组后每一小组的下标并不是零}}非递归法
思路:我们这个排序的核心就是1.一步步得到最小数组 2.一步步将两个小数组合并起来直到得到 大数组
所以可以在循环里嵌套循环,外面决定数组长度,里面循环将小数组排序合并,外循环设置每个小数组的相隔距离
public void mergrSort1(int[] array){int left = 0,right = array.length-1;int gap = 1;//gap负责将数组分为array.length/2while(gap<array.length){for (int i = 0; i < array.length; i+=2*gap) {//得到小一号的数组并且进行排序合并,里面for循环是为了得到最多组数组left = i;int mid = left+gap-1;right = mid+gap;if(mid >= array.length) mid=array.length-1;if(right>=array.length) right = array.length-1;merge(array,mid,left,right);}gap *= 2;//世界线收束,每次小数组排序好后,再将更大数组排序}}}总结:1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
8.计数排序
思路:将原数组遍历一遍,得到原数组的最大值和最小值,将最大值和最小值相减,得到它们的取值范围,创建一个新数组,然后将对应的值给到,和其相对相等的下标,(比如数组的值为1给到开辟数组的1下标,)然后遍历新数组,赋值给原数组
/*** 计数排序:* 时间复杂度:O(范围 + n )* 范围越大 越慢* 空间复杂度:O(范围)* 稳定性:* @param array*/public static void countSort(int[] array) {//1. 找最大值 和 最小值 来确定 计数数组的大小int maxVal = array[0];int minVal = array[0];for (int i = 1; i < array.length; i++) {if(array[i] < minVal) {minVal = array[i];}if(array[i] > maxVal) {maxVal = array[i];}}int len = maxVal - minVal + 1;int[] count = new int[len];//2. 遍历原来的数组array把 每个元素 放到对应的计数数组当中 进行计数for (int i = 0; i < array.length; i++) {int index = array[i];count[index-minVal]++;}//3.依次 遍历计数数组 O(范围)int index = 0;for (int i = 0; i < count.length; i++) {while (count[i] != 0) {array[index] = i+minVal;index++;count[i]--;}}}
总结
1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
2. 时间复杂度:O(MAX(N,范围))
3. 空间复杂度:O(范围)
4. 稳定性:稳定
相关文章:

JAVA-数据结构-排序
1.直接插入排序 1.原理:和玩扑克牌一样,从左边第二个牌开始,选中这个,和前面的所有牌比较,插在合适的位置 public static void insertsort(int[] arr){//直接插入排序for (int i 1; i < arr.length; i) {//此循环…...

初识数据结构--时间复杂度 和 空间复杂度
数据结构前言 数据结构 数据结构是计算机存储、组织数据的方式(指不仅能存储数据,还能够管理数据-->增删改)。指相互之间存在一种或多种特定关系的数据元素的集合。没有单一的数据结构对所有用途都有用,所以我们要学习各种的数据结构,比…...

Ubuntu QT 交叉编译环境搭建
文章目录 下载安装qtCreatornot a valid identifier 的错误 安装g下载并安装交叉编译器下载交叉编译器安装交叉编译器 下载编译 ARM 的Qt平台源码配置arm的QT平台 下载安装qtCreator 去QT下载官网下载对应需要的QT软件。 这里下载5.12.96版本的 改变安装包权限,…...

C语言中缓冲区底层实现以及数据输入的处理
C语言中缓冲区底层实现以及数据输入的处理 一、缓冲区的概念 在C语言的标准输入输出操作中,缓冲区(Buffer) 扮演着至关重要的角色。在计算机系统中,缓冲区是一块用于暂存数据的内存区域。在输入输出(I/O)…...

RocketMQ事务消息原理
一、RocketMQ事务消息原理: RocketMQ 在 4.3 版本之后实现了完整的事务消息,基于MQ的分布式事务方案,本质上是对本地消息表的一个封装,整体流程与本地消息表一致,唯一不同的就是将本地消息表存在了MQ内部&…...

【Java】IntelliJ IDEA开发环境安装
一、下载 官方地址:https://www.jetbrains.com/idea/ 点击Download直接下载 二、安装 双击安装包,点击Next 选择安装路径,点击Next 勾选安装内容 安装完成。 三、创建项目 打开IDEA,填写项目名称,选择项目安装路径…...
 实践:Goroutine之间的通信)
Go语言中的通道 (Channel) 实践:Goroutine之间的通信
1. 引言 在Go语言中,并发编程是其核心优势之一。与其他编程语言不同,Go语言推荐使用通道 (Channel) 来进行多线程或并发任务的协调与通信,而非使用锁机制。本文将介绍如何通过通道在多个goroutine之间进行通信,避免竞争条件和复杂…...
常用类(二)--String类的简单总结
文章目录 1.基本介绍1.1创建对象1.2找到对应下标的字符1.3找到对应字符的下标1.4指定位置开始遍历1.5反向进行遍历1.6大小写之间的转换1.7字符串转换为数组1.8元素的替换1.9字符串的分割1.10字符串的截取 2.StringBuilder和StringBuffer2.1 StringBuilder的引入2.2面试题目 1.基…...

Spring Boot开发:从入门到精通
Spring Boot开发:从入门到精通 当你在开发一个新的Java应用时,是否曾经感到苦恼于繁琐的配置和重复的代码?Spring Boot就像一位友好的助手,向你伸出援手,让开发变得轻松愉快。从这一单一框架中,你可以快速…...

《数据结构》--队列【各种实现,算法推荐】
一、认识队列 队列是一种常见的数据结构,按照先进先出(FIFO,First In First Out)的原则排列数据。也就是说,最早进入队列的元素最先被移除。队列主要支持两种基本操作: 入队(enqueue࿰…...

面试八股文对校招的用处有多大?--GDB篇
前言 1.本系列面试八股文的题目及答案均来自于网络平台的内容整理,对其进行了归类整理,在格式和内容上或许会存在一定错误,大家自行理解。内容涵盖部分若有侵权部分,请后台联系,及时删除。 2.本系列发布内容分为12篇…...

Unity用VS打开FGUI脚本变成杂项怎么处理?
在Unity中使用Visual Studio(VS)打开FGUI脚本时,如果脚本显示为杂项文件,这通常意味着VS没有正确识别或关联这些脚本文件。以下是一些解决此问题的步骤: 对惹,这里有一个游戏开发交流小组,大家…...
解释说明)
交叉熵损失函数(Cross-Entropy Loss Function)解释说明
公式 8-11 的内容如下: L ( y , a ) − [ y log a ( 1 − y ) log ( 1 − a ) ] L(y, a) -[y \log a (1 - y) \log (1 - a)] L(y,a)−[yloga(1−y)log(1−a)] 这个公式表示的是交叉熵损失函数(Cross-Entropy Loss Function)&#…...

和外部机构API交互如何防止外部机构服务不可用拖垮调用服务
引言 在现代的分布式系统和微服务架构中,服务之间的通信往往通过API进行,尤其是在与外部机构或第三方服务进行交互时,更需要通过API实现功能的集成。然而,由于外部服务的可控性较差,其服务的不可用性(如响…...

自动猫砂盆真的有必要吗?买自动猫砂盆不看这四点小心害死猫。
现在越来越多铲屎官选择购买自动猫砂盆来代替自己给猫咪铲屎,可是自动猫砂盆真的有必要吗?要知道,在现在忙碌的生活中,有很多人因为工作上的忙碌而不小心忽视了猫咪,猫咪的猫砂盆堆满粪便,要知道猫砂盆一天…...

国外解压视频素材哪里找?五个海外解压视频素材网站推荐
国外解压视频素材哪里找?五个海外解压视频素材网站推荐 如果你正在寻找国外的解压视频素材,那么今天这篇文章一定能帮助你。无论是修牛蹄、洗地毯,还是切肥皂、玩解压游戏等,下面分享的几个网站都是你找到高质量海外解压视频素材…...
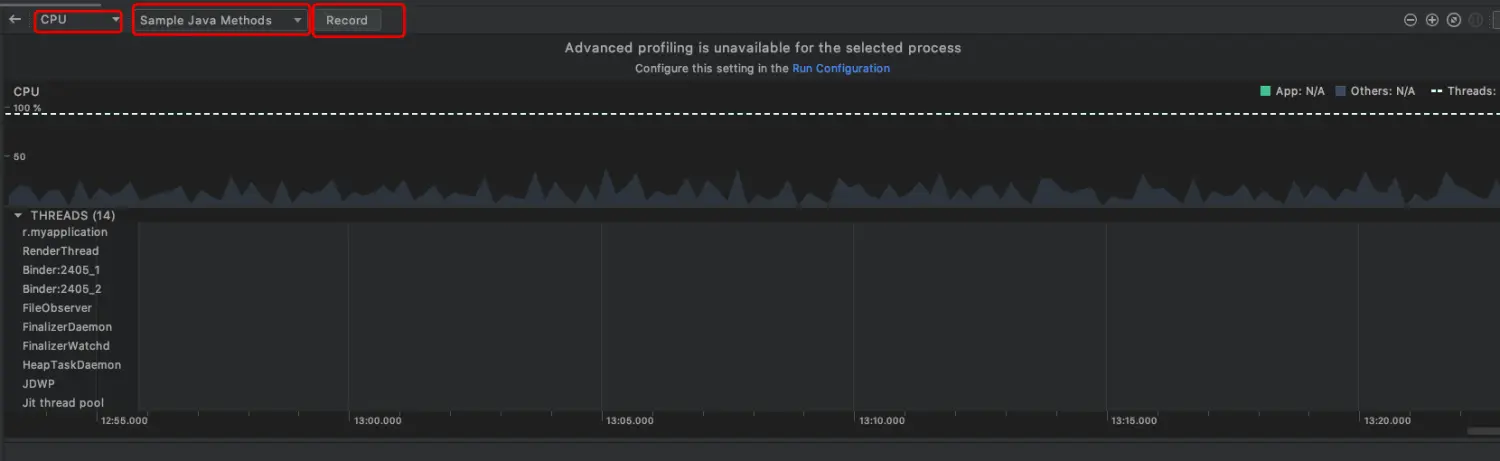
Android一个APP里面最少有几个线程
Android一个APP里面最少有几个线程 参考 https://www.jianshu.com/p/92bff8d6282f https://www.jianshu.com/p/8a820d93c6aa 线程查看 Android一个进程里面最少包含5个线程,分别为: main线程(主线程)FinalizerDaemon线程 终结者守护线程…...

位操作解决数组的花样遍历
文章目录 题目 一、思路: 二、代码 总结 题目 leetcodeT289 https://leetcode.cn/problems/game-of-life/description/ 一、思路: 这题思路很简单,对每个位置按照题目所给规则进行遍历,判断周围网格的活细胞数即可。但是题目要求…...

【面试宝典】深入Python高级:直戳痛点的题目演示(下)
目录 🍔 Python下多线程的限制以及多进程中传递参数的⽅式 🍔 Python是如何进⾏内存管理的? 🍔 Python⾥⾯如何拷⻉⼀个对象? 🍔 Python⾥⾯search()和match()的区别? 🍔 lambd…...

Hive数仓操作(十七)
一、Hive的存储 一、Hive 四种存储格式 在 Hive 中,支持四种主要的数据存储格式,每种格式有其特点和适用场景,不过一般只会使用Text 和 ORC : 1. Text 说明:Hive 的默认存储格式。存储方式:行存储。优点…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
