C#_带参数的委托进入队列执行
我们经常会遇到一些函数多个地方调用,但是只能单独执行的就需要把它放到队列中执行。
1.创建对应该方法的委托(传参和回参类型需要一致)。
//委托:
public delegate void CameraTaskDelegate(byte cs, ref byte[] buffer);//对应函数:
public void CameraSettingRead(byte cs, ref byte[] resultbuf)
{ //...
}
2.创建队列
// 定义一个队列来存储待执行的动作static Queue<Tuple<CameraTaskDelegate, byte, byte[]>> actionQueue = new Queue<Tuple<CameraTaskDelegate, byte, byte[]>>();
3.加入队列的方法
//加入队列的函数
static void EnqueueAction(Queue<Tuple<CameraTaskDelegate, byte, byte[]>> queue, CameraTaskD相关文章:

C#_带参数的委托进入队列执行
我们经常会遇到一些函数多个地方调用,但是只能单独执行的就需要把它放到队列中执行。 1.创建对应该方法的委托(传参和回参类型需要一致)。 //委托: public delegate void CameraTaskDelegate(byte cs, ref byte[] buffer);//对应函数: public void CameraSettingRead(by…...

【OpenCV】(二)—— 图片读取展示和保存
上一小节中我们成功安装了opencv,我们这次学习使用opencv最基础的功能,读取和展示图片,首先准备一张用于实验的样例图片【cat.jpg】如下: 然后就是创建一个python项目并导入相关依赖 import cv2读取图片 读取图片使用imread方法…...
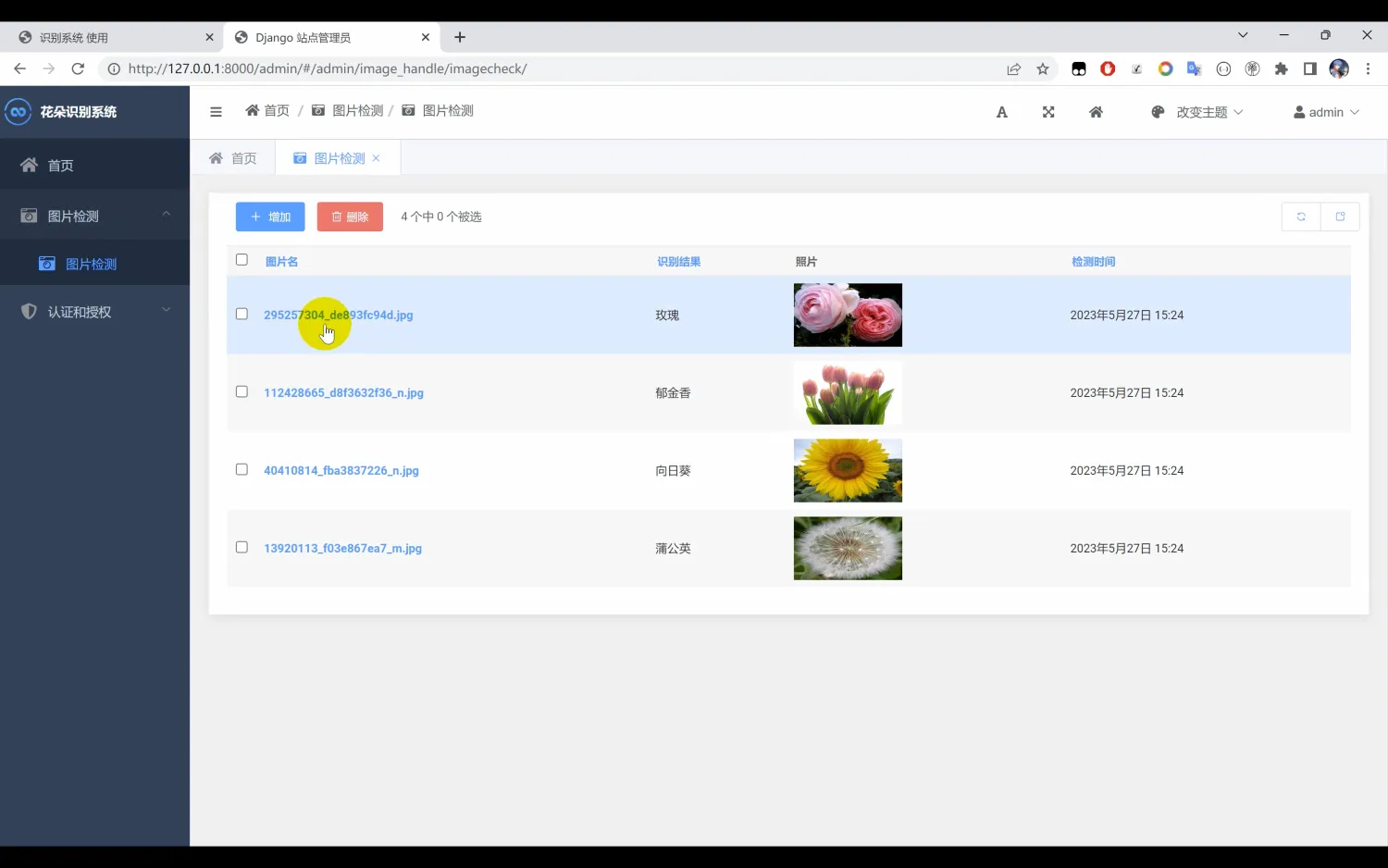
【花卉识别系统】Python+卷积神经网络算法+人工智能+深度学习+图像识别+算法模型
一、介绍 花朵识别系统。本系统采用Python作为主要编程语言,基于TensorFlow搭建ResNet50卷积神经网络算法模型,并基于前期收集到的5种常见的花朵数据集(向日葵、玫瑰、蒲公英、郁金香、菊花)进行处理后进行模型训练,最…...
k8s、prometheus、grafana数据采集和展示的链路流程
k8s集群中,容器级别的数据采集是由cAdvisor程序实现 cAdvisor # Container Advisor 容器顾问 cAdvisor程序是kubelet组件的一部分。 每个节点,包括master节点,都有一个kubelet系统服务, kukelet负责管理pod和容…...
-分布式fetcher和metrics存储/搜索)
sentinel dashboard改造落地设计实现解释(一)-分布式fetcher和metrics存储/搜索
背景 微服务是目前java主流架构,微服务架构技术栈有,服务注册中心,网关,熔断限流,服务同学,配置中心等组件,其中,熔断限流主要3个功能特性,限流,熔断,快速失败。Sentinel是阿里开源的熔断限流组件,sentinel dashboard是演示级别,表现在metrics采集是单机版,metri…...
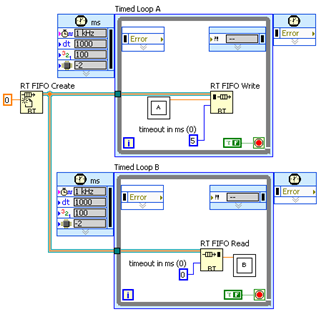
LabVIEW提高开发效率技巧----时序分析
一、什么是时序分析? 时序分析是优化LabVIEW程序性能的重要步骤。它通过分析程序各个部分的执行时间,帮助开发者找到程序运行中的瓶颈,并进行有针对性的优化。在LabVIEW中,Profile Performance and Memory工具是进行时序分析的关…...

python不用ide也能进行调试
import pdb pdb.set_trace()import pdb 和 pdb.set_trace() 是 Python 中用于调试代码的工具。以下是它们的具体含义和用法: import pdb pdb 是 Python 的内置调试器模块,允许开发者在运行时进行代码调试。 通过 import pdb 语句,你可以引入…...

Django学习笔记之Django基础学习
Django笔记 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 例如:第一章 Python 机器学习入门之pandas的使用 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录…...

smartctl 设置硬盘的 write-caching
sg3 一、sg3查看缓存状态 您可以使用sg_modes命令来查看SAS盘和SATA盘的缓存状态。例如,要查看/dev/sdb设备的缓存状态,您可以执行以下命令: sg_modes -p 8,0 /dev/sdb 二、sg3关闭机械盘写缓存状态(仅适用于SAS盘)…...

【Spring AI】Java实现类似langchain的向量数据库RAG_原理与具体实践
介绍一下RAG: 检索增强生成(RAG)是一种技术,它结合了检索模型和生成模型来提高文本生成的质量。通过从企业私有或专有的数据源中检索相关信息,并将这些信息与大型语言模型相结合,RAG能够显著减少模型产生幻…...

linux下使用systemctl设置开机自动运行程序
本文介绍在Linux下,使用systemctl设置开机自动运行程序,实现创建一个systemd服务单元文件,并启用该服务的方法。 1、创建.service文件 在/etc/systemd/system/目录下创建一个以.service结尾的文件,例如myapp.service:…...

复位电路的亚稳态
复位导致亚稳态的概念: 同步电路中,输入数据需要与时钟满足setup time和hold time才能进行数据的正常传输(数据在这个时间段内必须保持不变:1不能变为0,0也不能变为1),防止亚稳态; …...

针对考研的C语言学习(循环队列-链表版本以及2019循环队列大题)
题目 【注】此版本严格按照数字版循环队列的写法,rear所代表的永远是空数据 图解 1.初始化部分和插入部分 2出队 3.分部代码解析 初始化 void init_cir_link_que(CirLinkQue& q) {q.rear q.front (LinkList)malloc(sizeof(LNode));q.front->next NULL…...

系统架构设计师教程 第12章 12.4 信息系统架构案例分析 笔记
12.4 信息系统架构案例分析 ★★★★☆ 12.4.1 价值驱动的体系结构——连接产品策略与体系结构 1.价值模型概述 价值模型核心的特征可以简化为三种基本形式。 (1)价值期望值:表示对某一特定功能的需求,包括功能、质量和不同 级别质量的实用性。 (2)…...

web1.0,web2.0,web3.0 有什么区别 详解
Web 的发展经历了多个阶段,每个阶段都有其独特的特点和技术进步。下面是 Web 1.0、Web 2.0 和 Web 3.0 之间的主要区别和详细解释: Web 1.0 时间范围:大约在 1991 年至 1995 年。 Web 1.0 是互联网的最初形态,也被称为静态 Web…...
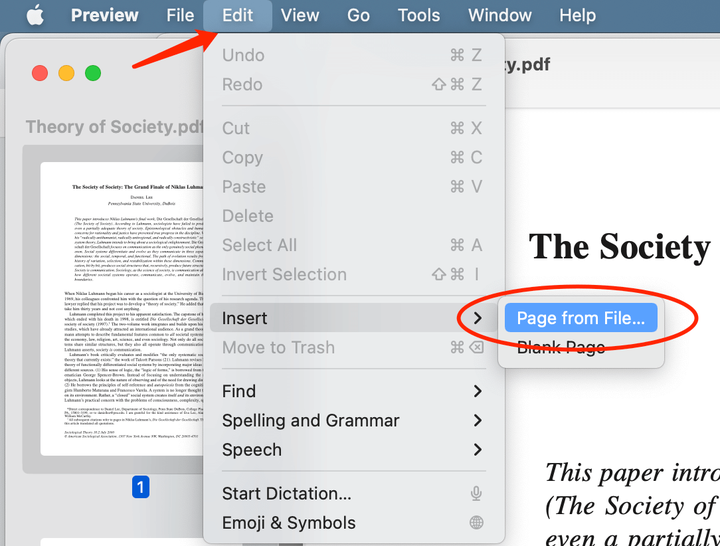
将图片添加到 PDF 的 5 种方法
需要一种称为 PDF 编辑器的特定工具才能将图片添加到 PDF。尽管大多数浏览器在查看和注释 PDF 文件方面都非常出色,但如果您使用图像到 PDF 技术,则只能将照片放入 PDF 中。无需修改即可将 PDF 文件恢复为原始格式的能力是使用此类软件程序甚至在线服务的…...

TiDB 优化器丨执行计划和 SQL 算子解读最佳实践
导读 在数据库系统中,查询优化器是数据库管理系统的核心组成部分,负责将用户的 SQL 查询转化为高效的执行计划,因而会直接影响用户体感的性能与稳定性。优化器的设计与实现过程充满挑战,有人比喻称这是数据库技术要持续攀登的珠穆…...

初学51单片机之I2C总线与E2PROM以及UART简单实例应用
这是I2C的系列的第三篇,这篇主要是写一个简单的程序来实践一下相关的内容。前面博主写过一个电子密码锁的程序初学51单片机之简易电子密码锁及PWM应用扩展_51单片机设计电子密码锁-CSDN博客 本篇主要是在此基础上修改下程序,让密码存储在E2PROM中&#…...

软考高级软件架构师论文——论Web系统的测试技术及其应用
【摘要】 本人于2023年8月参与了某地级市的市级机关电子政务信息系统的建设工作,该项目是该市机关的电子政务网建设计划的一部分,笔者在该项目中担任项目经理和系统分析师一职,主要负责项目的日常全面管理和质量保证与质量控制工作。该项目是基于WEB系统的,由于WEB系统具有…...

快速总结AFPN
AFPN: Asymptotic Feature Pyramid Network for Object Detection 解决的问题 特征金字塔架构的提出是为了解决尺度变化的问题,图像中物体真正有用的特征在顶部最高层需要通过多个中间尺度传播,并与这些尺度的特征交互,才能与底部的低层特征…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
