2024 第一次周赛
A:
题目大意
骑士每连续 i 天每天会得到 i 个金币,(i = 1, 2, 3 , …),那么展开看每一天可以得到的金币数:1 2 2 3 3 3 4 4 4 5 5 5 5 5 …
可以发现就是1个1 ,2个2, 3个3…,那么我们相同的一段分开来看,他们的加和正好就是这段里面相同数字的平方,而每一段里的数字个数就等于这段里的相同数字,那么我们想知道到第k 个数完整加了多少段就可以从1 开始遍历,如果 k = 7 ,那么前面加了完整的三段分别是1, 2 2 , 3 3 3,看成个数就是1 , 2 , 3,那么我们就能想到用数列加和公式 n * ( n + 1) / 2 算出来他的个数,那么剩下的不够下一段的个数直接乘下一段应为的数就好了,比如这个例子就是 7 - 3 * (3 + 1)/ 2 = 1;这个应该是一个 4 ,最后答案就是完整的段 加上剩余的段 = 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 1 * 4 = 18。
下面展示一些 `详细代码`。
#include<stdio.h>
int main()
{int k ;// 有k天scanf("%d",&k);//输入kint res = 0;//用来记录加到第 i 段时 总个数 >= kfor(int i =1;i <= 200;i ++){if(i*(i + 1) / 2 >= k){res = i;//记录break;//已经找到跳出循环}}int m = res - 1;//m 表示第k天之前加了多少个完整的段(就是相邻赐予金币数相同的一段天数)int cnt = k - m *(m + 1)/ 2;//记录完整的m段之后剩余的天数,最多满足完整的下一段int ans = 0;//记录总金币for(int i = 1;i <= m;i ++)//m段逐个加起来{ans = ans + (i * i);}ans += (m + 1) * cnt;//把剩余的加起来,因为前面已经加了m个完整的段,那么剩余的每一天得到的金币都是m + 1,并且剩余的天数即cnt不可能大于m + 1.printf("%d" , ans);//输出答案return 0;
}
B:
//题解:暴力,从1~n挨个搜索,对每次搜索到的数进行while循环以查找x出现的次数,多说无益直接看代码。
#include<stdio.h>
int main() {int n, x;scanf("%d%d", &n, &x);int count = 0;for (int i = 1; i <= n; i++)//从1~n挨个搜索{int j = i;while (j != 0){if (j % 10 == x) {//判断其最后一位是否为xcount++;}j /= 10;//去掉最后一位,继续向下查找}}printf("%d", count);return 0;
}
C:
特判:由题意得:n个位置,k个人,同时n≥k≥0;因此,k可以为n,也可以为0。考虑这两种情况。在k=n||k=0,这两种情况下,牛牛无法坐上过山车,因此最少位置和最多位置均为0;
正常情况:
最多:k<n,进行模拟,当k=1,010,最多有两个位置,k=2,010010,最多有四个位置,以此类推,k==t,最多有2t个位置。此时让我们想结果成立的条件,n≥t*3;但是如果条件不成立呢?最多已经是2t了,所以此时最多便是除去这k个人之外的所有位置,即n-t。
最少:除去特判的0,最少情况就只有1111__或者__1111的情况了,此时最少为1。
#include <bits/stdc++.h>
using namespace std;int main() {long long n, k;cin >> n >> k;if (k == n || k == 0)cout << "0 0" << '\n';else if (n >= k * 3)cout << "1 " << 2 * k << '\n';elsecout << "1 " << n - k << '\n';return 0;
}
D:


E:
这道题是一个图论的最短路径问题,节点1是中心节点,与其相连的边权为A,其他边权为B。题目要求找到从节点1出发,收集所有7个节点的宝石的最短时间。#include <stdio.h>int main() {int a, b; scanf("%d %d", &a, &b); // 输入A和B // 通过分析图的结构,最短路径可以直接计算如下:// 1. 对于节点1,与节点2, 3, 4, 5, 6, 7之间的距离分别为A。// 2. 两个相邻的非中心节点之间的路径为B。// 如果A的值大于等于B,则最短时间应该从节点1到达某个外围节点,然后沿着外围环路收集其他宝石。// 即最短时间为 a+ 5 * b // 如果A的值小于B,选出这两种情况的最小值,即min(a + 5 *b, 11* a); if (a + 5 * b > 11 * a){ printf("%d", 11 * a); return 0; } else { printf("%d", a + 5 * b );return 0; }}
F:
思路:看到题目最终让输出一个数首先要想能不能用二分来做,二分要首先确定边界,并且判断有无单调性,该题就能用二分来做, 二分枚举mex的值判断是否符合条件,二分判断之后最终将确定下来mex,不懂二分的可以看看这篇博客:https://blog.csdn.net/2301_80882026/article/details/135197055?ops_request_misc=%257B%2522request%255Fid%2522%253A%25225665E938-4BE3-45AB-B426-0C876A134A13%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fblog.%2522%257D&request_id=5665E938-4BE3-45AB-B426-0C876A134A13&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2blogfirst_rank_ecpm_v1~rank_v31_ecpm-1-135197055-null-null.nonecase&utm_term=%E4%BA%8C%E5%88%86&spm=1018.2226.3001.4450
#include<bits/stdc++.h>using namespace std;typedef long long ll;
typedef pair<int, int>PII;
const int N=1e6+10;
const int MOD = 1e9 + 7;
const int INF=0X3F3F3F3F;
const int dx[]={-1,1,0,0,-1,-1,+1,+1};
const int dy[]={0,0,-1,1,-1,+1,-1,+1};
const int M = 1e6 + 10;int t;
int n;
int a[N];
bool st[N];
bool check(int x)
{memset(st ,0, sizeof st);//初始化for(int i = 1; i <= n; i ++){int o = a[i];while(o && (o >= x || st[o])) o /= 2;st[o] = true;//能够到达的数}for(int i = 0; i < x; i ++) //注意mex的定义,要判断x符不符合只需要判断小于x的所有数是否均能到达{if(st[i] == 0) return false;//说明到达不了x}return true;
}
int main()
{cin >> t;while(t --){cin >> n;int res = 0;for(int i = 1; i <= n; i ++)cin >> a[i], res = max(res, a[i]);int l = 0, r = res + 1;while(l < r)//二分mex{int mid = (l + r + 1) >> 1;if(check(mid)) l = mid;else r = mid - 1;}cout << l << '\n';}return 0;
}
G:
//解析:
//如果n为偶数,那两两交换即可完成 即n/2;
//若n为奇数,则要多交换一次,即多出的那个数与谁交换都可以,为(n+1)/2次。
#include<stdio.h>
signed main()
{int n, m;scanf("%d", &n);for (int i = 1; i <= n; i++)scanf("%d", &m);if (n == 1) printf("-1");//只有n==1时不行else printf("%d", (n + 1) / 2);//可简称写为(n+1)/2;return 0;
}
H:
#include<stdio.h>
const int N=1e5+10;
bool st[N];
int main()
{int n;scanf("%d",&n);int cnt=0;for(int i=0;i<=9;i++)//先判断从1-10的好数,这要在之后的好数判定中有基础if(i%2==0) st[i]=true;for(int i=1;i<=n;i++)//暴力枚举从1到n的数{int x=i,sum=0;while(x)//求x的位数之和{int c=x%10;sum+=c;x/=10;}//位数之和是偶数,不大于它本身,是个好数if(sum<=i&&st[sum]&&sum%2==0){cnt++;st[i]=true;}}printf("%d\n",cnt);
}
相关文章:

2024 第一次周赛
A: 题目大意 骑士每连续 i 天每天会得到 i 个金币,(i 1, 2, 3 , …),那么展开看每一天可以得到的金币数:1 2 2 3 3 3 4 4 4 5 5 5 5 5 … 可以发现就是1个1 ,2个2, 3个3…,那么我…...

【数据脱敏方案】不使用 AOP + 注解,使用 SpringBoot+YAML 实现
文章目录 引入认识 YAML 格式规范定义脱敏规则格式脱敏逻辑实现读取 YAML 配置文件获取脱敏规则通过键路径获取对应字段规则原始优化后 对数据进行脱敏处理递归生成字段对应的键路径脱敏测试 完整工具类 引入 在项目中遇到一个需求,需要对交易接口返回结果中的指定…...

dbt doc 生成文档命令示例应用
DBT提供了强大的命令行工具,它使数据分析师和工程师能够更有效地转换仓库中的数据。dbt的一个关键特性是能够为数据模型生成文档,这就是dbt docs命令发挥作用的地方。本教程将指导您完成使用dbt生成和提供项目文档的过程。 dbt doc 命令 dbt docs命令有…...

【Windows】【DevOps】Windows Server 2022 安装ansible,基于powershell实现远程自动化运维部署 入门到放弃!
目标服务器安装openssh server参考 【Windows】【DevOps】Windows Server 2022 在线/离线 安装openssh实现ssh远程登陆powershell、scp文件拷贝-CSDN博客 注意:Ansible不支持Windows操作系统部署 根据官方说明: Windows Frequently Asked Questions —…...

深入理解 Parquet 文件格式
深入理解 Parquet 文件格式 深入理解 Parquet 文件格式一、引言二、为什么采用 Parquet 格式1. 行式存储的局限性2. 列式存储的优势 三、Parquet 的工作原理1. 文件结构2. 列块和页面3. 编码和压缩 四、具体数据实例1. 数据示例2. 行式存储 vs 列式存储3. 查询性能对比4. 压缩效…...

计算机挑战赛3
老式的计算机只能按照固定次序进行运算,华安大学就有这样一台老式计算机,计算模式为AB#C,和#为输入的运算符(可能是、-或*,运算符优先级与C一致),现给出A,B,C的数值以及和#对应的运算符…...

深度学习:循环神经网络—RNN的原理
传统神经网络存在的问题? 无法训练出具有顺序的数据。模型搭建时没有考虑数据上下之间的关系。 RNN神经网络 RNN(Recurrent Neural Network,循环神经网络)是一种专门用于处理序列数据的神经网络。在处理序列输入时具有记忆性…...

蓝桥杯刷题--幸运数字
幸运数字 题目: 解析: 我们由题目可以知道,某个进制的哈沙德数就是该数和各个位的和取整为0.然后一个幸运数字就是满足所有进制的哈沙德数之和.然后具体就是分为以下几个步骤 1. 我们先写一个方法,里面主要是用来判断,这个数在该进制下是否是哈沙德数 2. 我们在main方法里面调用…...

Node.js入门——fs、path模块、URL端口号、模块化导入导出、包、npm软件包管理器
Node.js入门 1.介绍 定义:跨平台的JS运行环境,使开发者可以搭建服务器端的JS应用程序作用:使用Node.Js编写服务器端代码Node.js是基于Chrome V8引擎进行封装,Node中没有BOM和DOM 2.fs模块-读写文件 定义:封装了与…...

多元线性回归:机器学习中的经典模型探讨
引言 多元线性回归是统计学和机器学习中广泛应用的一种回归分析方法。它通过分析多个自变量与因变量之间的关系,帮助我们理解和预测数据的行为。本文将深入探讨多元线性回归的理论背景、数学原理、模型构建、技术细节及其实际应用。 一、多元线性回归的背景与发展…...

域1:安全与风险管理 第1章实现安全治理的原则和策略
---包括OSG 1、2、3、4 章--- 第1章、实现安全治理的原则和策略 1、由保密性、完整性和可用性组成的 CIA 三元组。 保密性原则是指客体不会被泄露给 未经授权的主体。完整性原则是指客体保持真实性且只被经过授权的主体进行有目的的修改。 可用性原则指被授权的主体能实时和…...

【大数据】学习大数据开发应该从哪些技术栈开始学习?
学习大数据开发可以从以下几个技术栈和阶段入手。以下内容按学习顺序和重要性列出,帮助你逐步掌握大数据开发的核心技能: 1. 编程基础 Java:Hadoop 和许多大数据工具(如 Spark、Flink)的核心代码都是用 Java 编写的&…...

CentOS快速配置网络Docker快速部署
CentOS快速配置网络&&Docker快速部署 CentOS裸机Docker部署1.联通外网2.配置CentOS镜像源3.安装Docker4.启动Docker5.CentOS7安装DockerCompose Bug合集ERROR [internal] load metadata for docker.io/library/java:8-alpineError: Could not find or load main class …...

Grounded-SAM Demo部署搭建
目录 1 环境部署 2 Grounded-SAM Demo安装 3 运行Demo 3.1 运行Gradio APP 3.2 Gradio APP操作 1 环境部署 由于SAM建议使用CUDA 11.3及以上版本,这里使用CUDA 11.4版本。 另外,由于整个SAM使用的是Pytorch开发,因此需要Python环境&…...
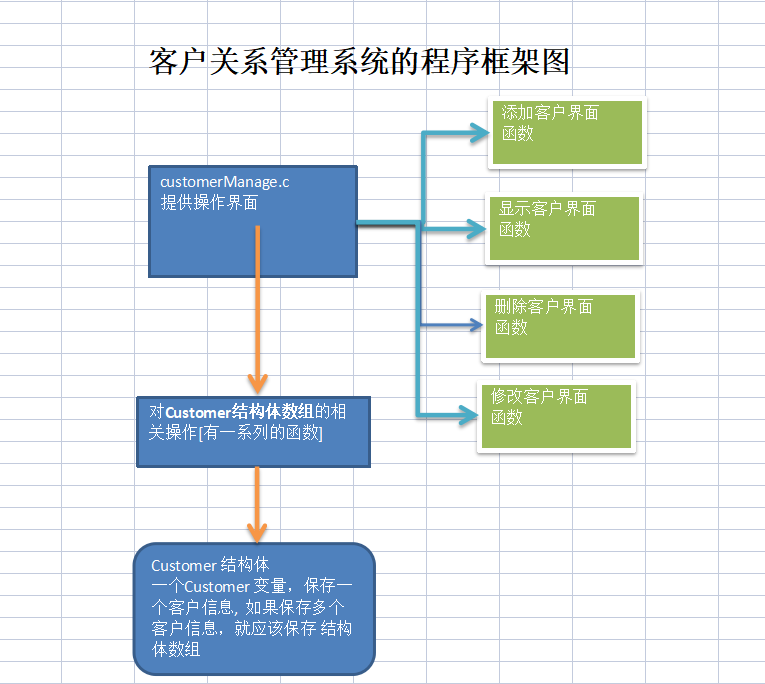
C语言 | 第十六章 | 共用体 家庭收支软件-1
P 151 结构体定义三种形式 2023/3/15 一、创建结构体和结构体变量 方式1-先定义结构体,然后再创建结构体变量。 struct Stu{ char *name; //姓名 int num; //学号 int age; //年龄 char group; //所在学习小组 float score; //成绩 }; struct Stu stu1, stu2; //…...

【论文阅读】Learning a Few-shot Embedding Model with Contrastive Learning
使用对比学习来学习小样本嵌入模型 引用:Liu, Chen, et al. “Learning a few-shot embedding model with contrastive learning.” Proceedings of the AAAI conference on artificial intelligence. Vol. 35. No. 10. 2021. 论文地址:下载地址 论文代码…...

OKHTTP 如何处理请求超时和重连机制
😄作者简介: 小曾同学.com,一个致力于测试开发的博主⛽️,主要职责:测试开发、CI/CD 如果文章知识点有错误的地方,还请大家指正,让我们一起学习,一起进步。 😊 座右铭:不…...

基于Springboot vue的流浪狗领养管理系统设计与实现
博主介绍:专注于Java(springboot ssm 等开发框架) vue .net php python(flask Django) 小程序 等诸多技术领域和毕业项目实战、企业信息化系统建设,从业十五余年开发设计教学工作☆☆☆ 精彩专栏推荐订阅☆☆☆☆☆不然下次找…...

爬虫案例——网易新闻数据的爬取
案例需求: 1.爬取该新闻网站——(网易新闻)的数据,包括标题和链接 2.爬取所有数据(翻页参数) 3.利用jsonpath解析数据 分析: 该网站属于异步加载网站——直接网页中拿不到,需要…...

SpringCloud 2023 Gateway的Filter配置介绍、类型、内置过滤器、自定义全局和单一内置过滤器
目录 1. Filter介绍2. Filter类型3. 内置过滤器3.1 请求头(RequestHeader)相关GatewayFilter Factory3.2 请求参数(RequestParameter)相关GatewayFilter Factory3.3 回应头(ResponseHeader)相关GatewayFilter Factory3.4 前缀和路径相关GatewayFilter Factory3.5 Default Filte…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
