数据结构——遍历二叉树
目录
什么是遍历二叉树
根据遍历序列确定二叉树
例题(根据先序中序以及后序中序求二叉树)
遍历的算法实现
先序遍历
中序遍历
后序遍历
遍历算法的分析
二叉树的层次遍历
二叉树遍历算法的应用
二叉树的建立
复制二叉树
计算二叉树深度
计算二叉树结点总数
什么是遍历二叉树
遍历定义-- 顺着某一条搜索路径巡访二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次(又称周游)。
- “访问”的含义很广,可以是对结点作各种处理,如:输出结点的信息、修改结点的数据值等,但要求这种访问不破坏原来的数据结构。
遍历目的-- 得到树中所有结点的一个线性排列。
遍历用途--它是树结构插入、删除、修改、查找和排序运算的前提,是二又树一切运算的基础和核心。
遍历方法

依次遍历二叉树的三个组成部分,便是遍历了整个二叉树。
若规定先左后右,则只有三种情况:


由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样“递归”进行。
先序(DLR)遍历二叉树的操作定义:
(1)访问根结点;
(2)先序遍历左子树;
(3)先序遍历右子树。
注:根的左子树遍历完(左子树的左子树、左子树的右子树...)才轮到根的右子树进行遍历。
示例如下:

中序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则
(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历右子树。
示例:

后序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则
(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根结点。
示例:
例题:

解析
先序: 先根结点A,再遍历根A的左子树,左子树遍历完,才轮到遍历右子树,左子树的根B,再根B的左子树,以D为根,再根D的左子树,没有就根D的右子树G,根G的左子树和右子树都没有,根D的树遍历完,再根B的右子树,没有,就可以遍历根A的右子树了,根C的左子树先遍历,以根E的树,根E的左子树没有,遍历根E的右子树,以H为根的左子树和右子树都没有,遍历根C的右子树,以F为根的左右子树都没有,先序遍历结束。
中序:先以A为根的左子树,再B为根的左子树,再以D为根的左子树,没有就输出根D,再根D的右子树G输出,以B为根的左子树结束就输出根B,再遍历B的右子树,没有就输出根A,再遍历根A的右子树,以C为根的左子树,再以E为根的左子树,没有就输出根E,根E的右子树H,根H的左子树没有,输出根H,根H的右子树没有,根C的左子树遍历完毕,输出根C,再遍历根C的右子树,以F为根的左子树没有,输出根F,根F的右子树没有。
后序:以A为根的左子树先遍历,以B为根的左子树先遍历,以D为根的左子树先遍历,没有就遍历根D的右子树,根G的左子树不存在,右子树也不存在,后序输出根结点G,根D的左右子树都遍历完了,输出根结点D,B的左子树遍历完,遍历其右子树,右子树不存在,输出根结点B,根A的左子树遍历完,遍历其右子树,根C的左子树先遍历,根E的左子树先遍历,不存在,遍历根E的右子树,根H的左右子树都不存在,输出根结点H,E的左右子树都遍历完,输出根结点E,C的左子树遍历完,遍历其右子树,根F的左右子树都不存在,输出根结点F,根C的左右结点都遍历完,输出根结点C,根A的左右子树都遍历完,输出根结点A。
请写出下图所示二叉树的先序、中序和后序遍历顺序。

根据遍历序列确定二叉树
- 若二叉树中各结点的值均不相同,则二叉树结点的先序序列、中序序列和后序序列都是唯一的。
- 由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一一棵二叉树
例题(根据先序中序以及后序中序求二叉树)
已知先序和中序序列求二叉树
例:已知二叉树的先序和中序序列,构造出相应的二叉树
先序:A B C D E F G H I J
中序:C D B F E A I H G J



首先从先序中可以知道这棵大树的根为A,已知根A后,从中序序列中可以得知C D B F E是这棵大树的左子树,I H G J是这棵大树的右子树;再从先序序列中B C D E F得知B是左子树的根,G H I J是右子树的根,再从中序序列中可以知道C D是根为B的树的左子树,F E是右子树,以此类推,可以构造相对应的二叉树。
已知后序和中序序列求二叉树
例:已知一棵二叉树的
中序序列:B D C E A F H G
后序序列:D E C B H G F A,请画出这棵二叉树。

类似的,我们可以先从后序序列中知道这棵大树的根结点为A,再从中序序列中得知B D C E是以A为根结点的左子树,F H G是其右子树,再从后序序列D E C B中知道B是左子树的根结点,F是左子树H G F的根结点,再从中序序列可以得出以B为根结点的树没有左子树,其右子树为D C E,以F为根结点的左子树不存在,其右子树为H G,以此类推可以画出完整的二叉树。
遍历的算法实现
先序遍历

步骤:

先序的遍历序列为ABCD
算法实现
Status PreOrderTraverse(BiTree T)
{if (T == NULL)return OK;//空二叉树else{visit(T);//访问根结点PreOrderTraverse(T->lchild);//递归遍历左子树PreOrderTraverse(T->rchild);//递归遍历右子树}
}

过程:指针T指向我们的二叉树的根结点,把根结点的指针T传递给前序遍历,判断T是否为空,此时不为空,输出A结点的数据域上的值,然后对左子树进行先序遍历,将当前结点的左孩子的地址传递给它自身,调用自身函数后,输出当前指针的数据域的值,也就是B结点的值,接下来访问B结点的左子树,为空返回,然后再访问B的右子树,此时T指向D结点,不为空输出其值,D结点的左右子树都为空,返回,依次返回到以A结点的树,其左子树遍历完毕,继续遍历其右子树。

中序遍历

步骤:

中序遍历序列:BDAC
算法实现
Status InOrderTraverse(BiTree T)
{if (T == NULL)return OK;else{InOrderTraverse(T->lchild);//递归遍历左子树visit(T);//访问根结点InOrderTraverse(T->rchild);//递归遍历右子树}
}后序遍历

步骤:

后序遍历序列:DBCA
算法实现
Status PostOrderTraverse(BiTree T)
{if (T == NULL)return OK;else{PostOrderTraverse(T->lchild);//递归遍历左子树PostOrderTraverse(T->rchild);//递归遍历右子树visit(T);//访问根结点}
}遍历算法的分析



如果去掉输出语句,从递归的角度看,三种算法是完全相同的,或说这三种算法的访问路径是相同的,只是访问结点的时机不同。

从虚线的出发点到终点的路径上,每个结点经过3次。
第1次经过时访问=先序遍历
第2次经过时访问=中序遍历
第3次经过时访问=后序遍历

二叉树的层次遍历

第一个访问根结点a,然后从左到右访问第二层,a的孩子b和f,再访问孩子的孩子。
对于一棵二叉树,从根结点开始,按从上到下、从左到右的顺序访问每一个结点。
每一个结点仅仅访问一次。
算法设计思路:使用一个队列
1、将根结点进队;
2、队不空时循环:从队列中出列一个结点*p,访问它;
- 若它有左孩子结点,将左孩子结点进队;
- 若它有右孩子结点,将右孩子结点进队。

遍历描述:首先,根结点a入队, 队列开始出队,第一个结点是
a,a出队,然后把a的左右孩子b、f入队,再从队列中拿出最前一个结点b出队,把它的左右孩子c、d入队,再拿出f出队,把它的左孩子g入队,现在队列中还有cdg,把c出队,它的左右孩子入队,没有就拿下一个结点出队,以此类推。
代码实现:
使用队列类型定义如下
typedef struct
{BTNode data[MaxSize];//存放队中元素int front, rear;//队头和队尾指针
}SqQueue; //顺序循环队列类型二叉树层次遍历算法:
void LevelOrder(BTNode* b)
{BTNode* p;SqQueue* qu;InitQueue(qu);//初始化队列enQueue(qu,b);//根结点指针进入队列while (!QueueEmpty(qu)){deQueue(qu,p);//出队结点printf("%c",p->data);//访问结点pif (p->lchild != NULL)enQueue(qu,p->lchild);//有左孩子时将其出队if (p->rchild != NULL)enQueue(qu, p->rchild);//有右孩子时将其出队}
}二叉树遍历算法的应用
二叉树的建立
- 按先序遍历序列建立二叉树的二叉链表
例:已知先序序列为:ABCDEGF
(1)从键盘输入二叉树的结点信息,建立二叉树的存储结构;
(2)在建立二叉树的过程中按照二叉树先序方式建立;

用#表示空字符
代码实现
Status CreateBiTree(BiTree& T)//链式存储
{scanf(&ch);//cin>>ch;if (ch == "#")T = NULL;else{if (!(T=(BiTNode*)malloc(sizeof(BiTree))))//从内存当中分配一个结点空间exit(OVERFLOW);//T=new NiTNode;T->data = ch;CreateBiTree(T->lchild);//构造左孩子CreateBiTree(T->rchild);//构造右孩子}return OK;
}//CreateBiTree复制二叉树
如果是空树,递归结束;
否则,申请新结点空间,复制根结点
- 递归复制左子树
- 递归复制右子树
代码实现
int Copy(BiTree T, BiTree& NewT)
{if (T == NULL){NewT = NULL;return 0;//如果是空树,返回0}else{NewT = new BiTNode; NewT->data = T->data;//复制结点数据Copy(T->lchild, NewT->lchild);//递归复制左子树Copy(T->rchild, NewT->rchild);//递归复制右子树}
}计算二叉树深度
- 如果是空树,则深度为0;
- 否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。
代码实现
int Depth(BiTree T) {if (T == NULL)return 0;else {m = Depth(T->lchild);//求左子树的深度n = Depth(T->rchild);//求右子树的深度if (m > n)return (m + 1);else return (n + 1);}
}计算二叉树结点总数
- 如果是空树,则结点个数为0;
- 否则,结点个数为左子树的结点个数+右子树的结点个数再+1。
代码实现
int NodeCount(BiTree T) {if (T == NULL)return 0;else return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}计算二叉树叶子结点数
- 如果是空树,则叶子结点个数为0;
- 否则,为左子树的叶子结点个数+右子树的叶子结点个数。
代码实现
int LeadCount(BiTree T) {if (T == NULL) return 0;if (T->lchild == NULL && T->rchild == NULL)return 1;//如果是叶子结点返回1elsereturn LeafCount(T->lchild) +LeafCount(T->rchild);
}相关文章:

数据结构——遍历二叉树
目录 什么是遍历二叉树 根据遍历序列确定二叉树 例题(根据先序中序以及后序中序求二叉树) 遍历的算法实现 先序遍历 中序遍历 后序遍历 遍历算法的分析 二叉树的层次遍历 二叉树遍历算法的应用 二叉树的建立 复制二叉树 计算二叉树深度 计算二…...

【Ubuntu】在Ubuntu上安装IDEA
【Ubuntu】在Ubuntu上安装IDEA 零、前言 最近换了Ubuntu系统,但是还得是要写代码,这样就不可避免地用到IDEA,接下来介绍一下如何在Ubuntu上安装IDEA。 壹、下载 这一步应该很容易的,直接打开IDEA的下载页面,点击下…...

解决:gpg: 从公钥服务器接收失败:服务器故障
当你添加密钥时报错,可以按照下面的步骤,依次输入。 # 停止 Network Manager 服务 sudo service network-manager stop# 删除 Network Manager 的状态文件 sudo rm /var/lib/NetworkManager/NetworkManager.state# 重新启动 Network Manager 服务 sudo …...

支持向量机SVM
目录 1 SVM直觉理解2. 软硬间隔3. 升维转换及核技巧入门 参考资料 1 SVM直觉理解 通过一条直线将两类数据分开,并且当有新的数据加入时,通过该条直线就能判别其属于哪一类 为了区分两类数据,N为数据的样本数,M为维度数…...

斯坦福UE4 C++课学习补充25:AI感知组件
文章目录 一、引入感知组件并绑定委托二、优化角色旋转 一、引入感知组件并绑定委托 PawnSensingComponent是UE中用于感知其他 Pawn(或 Actor)存在的一个组件,常用于 AI 角色的视觉、听觉等感知功能。它为 AI 提供了基础的感知能力ÿ…...

大模型 memory 记忆 缓存的应用
在探讨大模型的“memory”(记忆)功能时,我们通常会涉及缓存、存储以及如何有效管理和利用这些记忆来增强模型的性能。以下是对大模型memory记忆、缓存及相关概念的详细分析: 一、大模型的记忆功能 大模型,特别是大型…...

perl 给特定文件加上特定内容
perl 给特定文件加上特定内容 给所有的输入文件,加上特定的内容 本例中,给所有的输入文件内加入## Copyright xxx 如果检测到已经有## Copyright字样的行,那么不添加,具体代码如下。 可以使用该脚本,给所有的verilog文…...

全面解析网络性能监控系统与网络故障排除技巧,助力IT运维高效管理
目录 一、什么是网络性能监控系统? 1.1 网络性能监控系统的定义与作用 二、网络性能监控的关键指标 三、网络故障排除的重要性 3.1 为什么网络故障排除至关重要? 3.2 网络故障的常见类型 四、如何高效进行网络故障排除? 4.1 系统化的…...

Centos7 搭建单机elasticsearch
以下是在 CentOS 7 上安装 Elasticsearch 7.17.7 的完整步骤:(数据默认保存在/var/lib/elasticsearch下,自行更改) 一、装 Java 环境 Elasticsearch 是用 Java 编写的,所以需要先安装 Java 运行环境。 检查系统中是…...

【前端】Bootstrap:JavaScript 组件与插件
Bootstrap 不仅提供了强大的 CSS 工具和组件,还内置了丰富的 JavaScript 组件和插件。这些 JavaScript 组件能够增强网页的交互性,让开发者在不编写大量 JavaScript 代码的情况下快速实现各种动态效果。Bootstrap 的 JavaScript 组件基于 jQuery…...

部署 Open WebUI
1. 安装docker 2.启动Hyper-v 3.下载 安装 WSL wsl --update wsl --install 4. 打开 DeskDocker 5. 打开 运行 ollama 参考 Windows 部署 ollama-CSDN博客 6. 部署 运行 open webui docker docker run -d -p 3000:8080 --add-hosthost.docker.internal:host-gateway -v o…...

HUAWEI_HCIA_实验指南_Lib2.1_交换机基础配置
1、原理概述 交换机之间通过以太网电接口对接时需要协商一些接口参数,比如速率、双工模式等。交换机的全双工是指交换机在发送数据的同时也能够接收数据,两者同时进行。就如平时打电话一样,说话的同时也能够听到对方的声音。而半双工指在同一…...

第4天:用户界面和布局补充材料——`activity_login.xml`解读
下面是对“第4天:用户界面和布局补充材料”该文学习的更深层次的补充材料,对 activity_login.xml 文件的理解。 下面对activity_login.xml’ 文件中每一行进行详细解释: <?xml version"1.0" encoding"utf-8"?>声…...

《深入浅出LLM基础篇》(五):Propmt工程优化
🎉AI学习星球推荐: GoAI的学习社区 知识星球是一个致力于提供《机器学习 | 深度学习 | CV | NLP | 大模型 | 多模态 | AIGC 》各个最新AI方向综述、论文等成体系的学习资料,配有全面而有深度的专栏内容,包括不限于 前沿论文解读、…...

基于WebSocket实现简易即时通讯功能
代码实现 pom.xml <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId> </dependency> <dependency><groupId>org.springframework.boot</groupId><artifa…...

2012年国赛高教杯数学建模D题机器人避障问题解题全过程文档及程序
2012年国赛高教杯数学建模 D题 机器人避障问题 图1是一个800800的平面场景图,在原点O(0, 0)点处有一个机器人,它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物,障碍物的数学描述如下表:…...

Linux驱动开发——设备树
文章目录 1 什么是设备树?2 DTS、DTB和DTC3 DTS语法3.1 dtsi头文件3.2 设备节点3.3 标准属性3.4 根节点compatible属性3.5 向节点追加或修改内容 4 创建小型模板设备树5 设备树在系统中的体现6 绑定信息文档7 设备树常用OF操作函数7.1 查找节点的OF函数7.2 查找父/子…...

spring boot 2.7整合Elasticsearch Java client + ingest attachment实现文档解析
一、软件环境 软件版本号备注Spring boot2.7.23.x版本建议使用ElasticSearch8.xElasticSearch7.17.4ElasticSearch 7.x 可使用JDK 8 ElasticSearch 8.x 要求使用JDK 11 二、安装ElasticSearch 下载地址:https://artifacts.elastic.co/downloads/elasticsearch/el…...

一、PyCharm 基本快捷键总结
PyCharm 快捷键 前言一、编辑(Editing)二、查找/替换(Replace)三、运行(Running)四、重构(Refactoring)五、基本(General) 前言 下面我们将学习一些 Pycharm 中的快捷键来帮我们更好的使用工具。 一、编辑(Editing) 快捷键快捷键…...
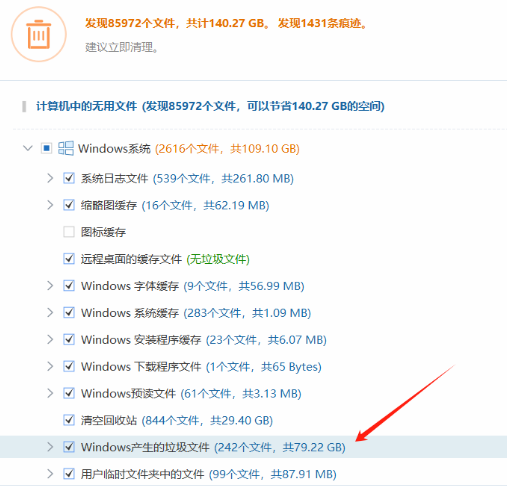
Windows系统C盘爆满了,如何清理?
Windows系统C盘爆满了,如何清理? 大家好,我是秋意零。 相信使用过Windows系统的朋友,都见过C盘那道靓丽的 “红色风景线” ! 我自己的Win10系统,已经使用了4-5年时间了。最近频频出现"红色风景线&q…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...
