小红的行列式构造
链接:登录—专业IT笔试面试备考平台_牛客网
来源:牛客网
题目描述
小红希望你构造一个3阶行列式,满足每个元素的绝对值不小于1,且行列式的值等于xxx。你能帮帮她吗?
输入描述:
一个整数xxx −100≤x≤100
输出描述:
输出三行,每行三个整数aij,用于表示构造的行列式。 请保证−109≤aij≤109
示例1
输入
复制0
0
输出
复制1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
思路:
[a b c]
[d e f]
[g h i]
行列值为a*(e*i-f*h)-b*(d*i-f*g)+c*(d*h-e*g)
设a==b==c,都为1
得e*i-f*h-d*i+f*g+d*h-e*g=d(h-i)+f*(g-h)+e*(i-g)
设d==f+e,d=2,f=e=1
得h-i,让h-i=x
设i=任意数,即h=x+i;
#include<bits/stdc++.h>
using namespace std;
int x;
int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>x;if(x==0){cout<<"1 1 1\n1 1 1\n1 1 1";}else cout<<"1 1 1\n2 1 1\n1 "<<x+x<<" "<<x;//i可以为任意数
}
相关文章:

小红的行列式构造
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 小红希望你构造一个3阶行列式,满足每个元素的绝对值不小于1,且行列式的值等于xxx。你能帮帮她吗? 输入描述: 一个整数xxx −100≤x≤100 输出描…...

pyflink过滤kafka数据
from pyflink.table import (TableEnvironment, EnvironmentSettings)# 输入、输出、过滤条件 columns_in [ ... ]columns_out [ ... ] filter_condition "name 蒋介石 and sex 男"# 创建执行环境t_env TableEnvironment.create(EnvironmentSettings.in_stream…...

Webpack 完整指南
🌈个人主页:前端青山 🔥系列专栏:Webpack篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来webpack篇专栏内容:webpack介绍 目录 介绍 一、webpack 1.1、webpack是什么 1.2 webpack五个核心配置 1.…...

如何在 Ubuntu20.04 安装FTP Server vsftpd
1.安装: sudo apt-get install vsftpd 2.启动 sudo service vsftpd start //启动 sudo service vsftpd stop //停止 sudo service vsftpd restart //重新启动 3.打开配置文件 sudo nano /etc/vsftpd.conf 4.配置:限制在指定目录&…...

基于FPGA的DDS信号发生器(图文并茂+深度原理解析)
篇幅有限,本文详细源文件已打包 至个人主页资源,需要自取...... 前言 DDS(直接数字合成)技术是先进的频率合成手段,在数字信号处理与硬件实现领域作用关键。它因低成本、低功耗、高分辨率以及快速转换时间等优点备受认可。 本文着重探究基于 FPGA 的简易 DDS 信号发生器设…...

QT:绘制事件和定时器
1.绘制时针 xx.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTimer> #include<QPainter> #include <QTime>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpubl…...

【算法——递归回溯】
这个东西还是很重要的,直接决定了你的动态规划章节的学习深度 78. 子集 方法1: vector<vector<int>>V; void dfs(vector<int> v,vector<int> nums,int index) {if(indexnums.size()) V.push_back(v);else{v.push_back(nums[i…...

手机在网状态接口的使用和注意事项
手机在网状态接口是用于查询手机号码在运营商数据库中的实时状态的工具,这种接口在互联网金融、贷款、租赁、保险等相关行业中尤为重要,因为它可以帮助这些行业进行更有效的风控审核。以下是对手机在网状态接口的详细介绍: 一、手机在网状态…...

WebGl 使用uniform变量动态修改点的颜色
在WebGL中,uniform变量用于在顶点着色器和片元着色器之间传递全局状态信息,这些信息在渲染过程中不会随着顶点的变化而变化。uniform变量可以用来设置变换矩阵、光照参数、材料属性等。由于它们在整个渲染过程中共享,因此可以被所有使用该着色…...

Leetcode 划分字母区间
题目要求: 将字符串 s 划分成尽量多的片段,保证每个片段中出现的字母不会出现在其他片段中。 具体解释如下: 尽量多的片段:题目要求的是在划分过程中,我们要尽量让划分的片段数量最大化,而不是最少化。每…...

可编辑div遇到的那些事
在日常开发中有时可能会遇到input 或 textarea 不能满足的开发场景,比如多行输入的情况下,textarea 的右下角icon 无法去除, 所以此时可以使用div 设置可编辑状态,完成功能开发,在开发的过程中仍会遇到一下问题。 1,如…...

什麼是高速HTTP代理?
高速HTTP代理是一種用於加速和優化互聯網連接的技術。它通過在用戶和目標網站之間充當仲介伺服器,幫助用戶快速訪問網路資源。HTTP代理不僅可以提高訪問速度,還能提供一定程度的隱私保護和安全性。 高速HTTP代理的工作原理 HTTP代理伺服器位於用戶設備…...

三子棋(C 语言)
目录 一、游戏设计的整体思路二、各个步骤的代码实现1. 菜单及循环选择的实现2. 棋盘的初始化和显示3. 轮流下棋及结果判断实现4. 结果判断实现 三、所有代码四、总结 一、游戏设计的整体思路 (1)提供一个菜单让玩家选择人机对战、玩家对战或者退出游戏…...
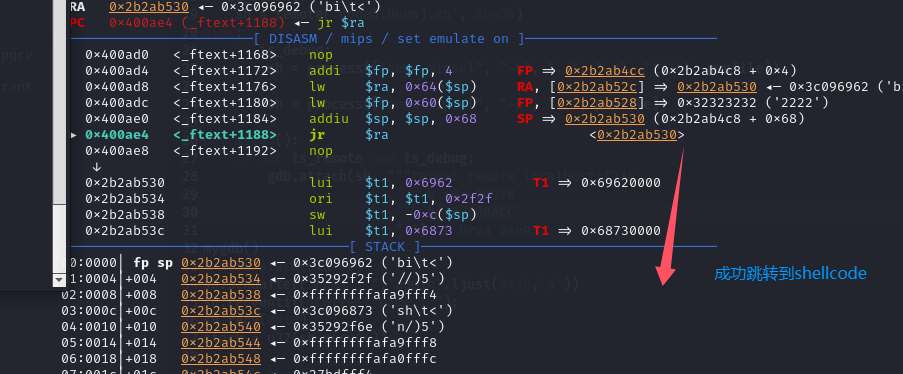
HWS赛题 入门 MIPS Pwn-Mplogin(MIPS_shellcode)
解题所涉知识点: 泄露或修改内存数据: 堆地址:栈地址:栈上数据的连带输出(Stack Leak) && Stack溢出覆盖内存libc地址:BSS段地址: 劫持程序执行流程:[[MIPS_ROP]] 获得shell或flag&am…...

纯血鸿蒙启动公测,爱加密鸿蒙加固平台发布,助力鸿蒙应用安全运营!
鸿蒙系统打破了移动操作系统两极格局,实现操作系统核心技术的自主可控、安全可靠,在神州大地上掀起一波科技革新的浪潮,HarmonyOS NEXT成为大型企业必须要布局的应用系统之一。 HarmonyOS NEXT于10月8日正式开启公测,距离面向全体…...

MySQL中 truncate、drop和delete的区别
MySQL中 truncate、drop和delete区别 truncate 执行速度快,删除所有数据,但是保留表结构不记录日志事务不安全,不能回滚可重置自增主键计数器 drop 执行速度较快,删除整张表数据和结构不记录日志事务不安全,不能回…...
什么开放式耳机值得买?开放式耳机推荐排行榜!
长时间佩戴传统入耳式耳机有时可能会影响耳道健康,鉴于此,转而选择不入耳设计的开放式耳机就成了不少人的新倾向,它们有助于减少细菌滋生和耳道闷热的烦恼。为了帮助大家找到合适的选项,下面我将列举一些市面上口碑不错的开放式耳…...

Apache Doris的分区与分桶详解
目录 第一章 Doris介绍和分区分桶作用 1.1 Doris背景介绍 1.2 分区与分桶的意义 第二章 原理解析 2.1 分区机制 2.1.1 定义 2.1.2 类型 2.1.3 工作原理 2.2 分桶机制 2.2.1 概念 2.2.2 实现方式 2.2.3 与分区的关系 第三章 手动分区与自动分区对比 3.1 手动分区 …...
info详解)
docker详解介绍+基础操作 (二)info详解
1 docker相关信息和优化配置 1)查看docker版本详解 rootzz:~# docker version Client: Docker Engine - CommunityVersion: 27.3.1API version: 1.47Go version: go1.22.7Git commit: ce12230Built: Fri Sep 20 11:40:…...

C0023.在Clion中创建控件,对控件进行提升为自定义控件的步骤
新建Ui界面文件 修改新生成的ui文件头文件 关闭之前打开的ui文件,如上图Qt Designer中打开的,然后修改新生成的ui文件对应的头文件,改成自己需要的控件类即可。 提升控件为自定义类 将如下头文件中的类名和头文件名输入到提升窗口中&#…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...
