PCL 3D-SIFT关键点检测(曲率不变特征约束
PCL点云算法汇总及实战案例汇总的目录地址链接:
PCL点云算法与项目实战案例汇总(长期更新)
一、概述
3D-SIFT(Scale-Invariant Feature Transform)关键点检测是用于点云分析的一种有效方法,具有尺度不变性和旋转不变性。在处理复杂场景和物体识别时,通过对点云的多尺度空间构建和局部特征的提取,可以提取稳定的特征点。本示例结合了曲率不变的特性,通过对点云的法向量进行计算,提取出更具几何稳定性的SIFT关键点。
1.1原理
SIFT算法的核心思想是通过尺度空间中的特征检测来找到图像中的稳定特征点。三维SIFT通过计算点云的法向量和曲率来替代二维图像的灰度值,并在不同的尺度下提取稳定的特征点。</
相关文章:

PCL 3D-SIFT关键点检测(曲率不变特征约束
PCL点云算法汇总及实战案例汇总的目录地址链接: PCL点云算法与项目实战案例汇总(长期更新) 一、概述 3D-SIFT(Scale-Invariant Feature Transform)关键点检测是用于点云分析的一种有效方法,具有尺度不变性和旋转不变性。在处理复杂场景和物体识别时,通过对点云…...

Android上的AES加密
基础算法说明 https://www.youtube.com/watch?vlnKPoWZnNNM 虽然这个视频讲的非常详细,但是涉及到具体底层算法,大致流程 1. 将数据转成HEX或者byte array 2.将数据分层一块块等大小的数据 3.将数据和key 进行一次混合,加密之后的输出&…...

安全测试的漏洞类型
目录 一、安全测试的定义 二、安全测试的分类 1、静态扫描 2、内存扫描 3、动态安全测试 三、安全测试主要关注哪些方面的漏洞 漏洞一:SQL注入 漏洞二:XSS 漏洞三:暴力破解 漏洞四:文件包含文件上传漏洞 漏洞五&#…...

51 | 适配器模式:代理、适配器、桥接、装饰,这四个模式有何区别?
前面几篇文章我们学习了代理模式、桥接模式、装饰器模式,今天,我们再来学习一个比较常用的结构型模式:适配器模式。这个模式相对来说还是比较简单、好理解的,应用场景也很具体,总体上来讲比较好掌握。 关于适配器模式…...

ORM框架简介
什么是ORM? ORM(Object-Relational Mapping,对象关系映射)是一种编程技术,用于在关系数据库和对象程序语言之间转换数据。ORM框架允许开发者以面向对象的方式来操作数据库,而不需要编写复杂的SQL语句。简单…...

Windows系统上根据端口号查找对应进程
“开始”-“运行”,输入cmd,打开命令行窗口,输入netstat和findstr的组合,找出占用了4118的端口的进程 根据上述PID,使用tasklist和findstr的组合,找出对应进程是dsa.exe 要想kill此进程,可以打开…...
一文通透OpenAI o1:从CoT、Quiet-STaR、Self-Correct、Self-play RL、MCST等技术细节到工程复现
前言 注意,本文自10.12日起,正在每天更新的过程中,包括已写的部分也在不断修改(以增加更多技术细节、更加通俗易懂) 预计10.20完成第一版,10月底修订到第二版——具体修订记录详见本文文末.. 可能是去年写或讲的关于ChatGPT原理的…...

如何解决与kernel32.dll相关的常见错误:详细指南解析kernel32.dll文件缺失、损坏或错误加载问题
当你的电脑中出现错误kernel32.dll丢失的问题,会导致电脑不能出现正常运行,希望能够有效的帮助你有效的将丢失的kernel32.dll文件进行修复同时也给大家介绍一些关于kernel32.dll文件的相关介绍,希望能够有效的帮助你快速修复错误。 kernel32.…...
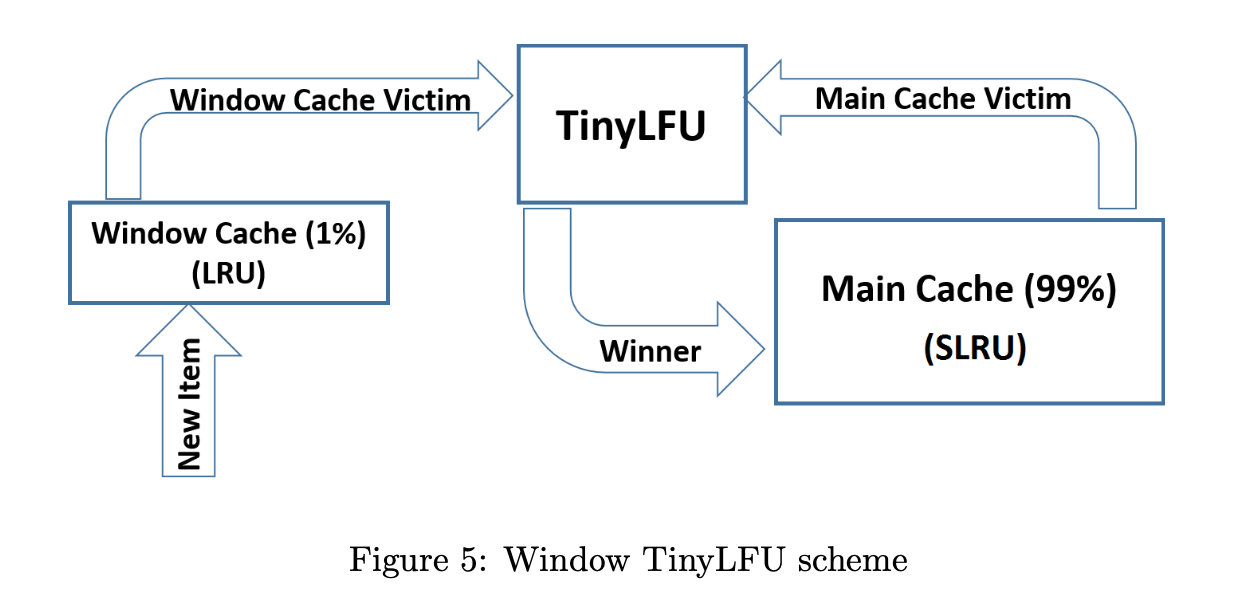
Caffeine Cache解析(一):接口设计与TinyLFU
Caffeine is a high performance Java caching library providing a near optimal hit rate. 自动加载value, 支持异步加载基于size的eviction:frequency and recency基于时间的过期策略:last access or last write异步更新valuekey支持weak referenceva…...

深入探索LINUX中AWK命令:强大的文本处理工具
深入探索LINUX中AWK命令:强大的文本处理工具 AWK 是一种编程语言,专为文本和数据处理设计,它以其强大的文本处理能力和简洁的语法在 Unix/Linux 系统中占据了重要地位。AWK 程序由一系列的模式(pattern)和动作(action)组成,对于输…...

数字化转型:解决项目管理困境的新路径
在当今这个飞速发展的数字化时代,企业如同在汹涌波涛中航行的船只,承受着前所未有的变革压力。而作为企业运作核心环节之一的项目管理,同样面临着巨大的挑战。 传统项目管理模式中的种种问题,犹如顽固的礁石,阻碍着项目…...

Arthas常用的命令(三)--monitor、jad 、stack
monitor:监控方法的执行情况 监控指定类中方法的执行情况 用来监视一个时间段中指定方法的执行次数,成功次数,失败次数,耗时等这些信息 参数说明 方法拥有一个命名参数 [c:],意思是统计周期(cycle of ou…...

Power BI之常用DAX函数使用介绍——提供数据源练习
前述: 本次使用数据是包含产品表、客户表、区域表、销售订单表的一份销售订单数据,数据源链接如下: 链接:https://pan.baidu.com/s/1micl_09hFrgz2aUBERkeZg 提取码:y17e 一、CALCULATE 1.语法结构 语法结构CALCUL…...
的详解以及代码演示)
SQL-触发器(trigger)的详解以及代码演示
一、触发器的概念 触发器是一种特殊的存储过程,但是触发器不存在输入和输出参数,所以不能被显式的去调用,而是与特定的表相关联,当表中的数据发生变化时,触发器被激活并执行其定义的SQL代码。触发器可以是行级触发器&…...

【devops】x-ui 实现一键安装 x-ray 打造高速国际冲浪 | xray管理平台
一、部署X-UI篇 1、Github 地址&说明 github地址如下: https://github.com/FranzKafkaYu/x-ui?tabreadme-ov-file 2、一键部署 2.1、更新并安装curl #Ubuntu、Deibian系统 apt update && apt upgrade -y apt install curl -y #CentOS7 系统 yum…...

Linux系统编程——进程标识、进程创建
一、进程标识(pid) 每个进程都有一个非负整数形式的唯一编号,即 PID。PID 在任何时刻都是唯一的,但是可以重用,当进程终止并被回收以后,其 PID 就可以为其它进程所用。进程的 PID 由系统内核根据延迟重用算…...

【超级福利】openMind开源实习来袭,奖励高达万元,解锁你的AI实践新篇章!
亲爱的小伙伴们,是不是梦想着能在真实的项目中大展拳脚,却又苦于找不到合适的舞台?别担心,OpenI启智社区携手openMind Library工具链,为你量身打造了一场开源实习盛宴,保证让你的学习不再无聊,技…...

React JSX 使用条件语句渲染UI的两种写法
只针对函数组件 1. 第一种写法: function App({ id }) {return id1? <h1>hello</h1> : <h1>world</h1>; } 或者: function App({ id }) {return (<h1>{id1 && "hello" || id2 && "wo…...

谷歌-BERT-第四步:模型部署
1 需求 需求1:基于gradio实现大模型的WEB UI交互界面 2 接口 3 示例 import gradio as gr from transformers import *classifier pipeline("text-classification", model"./model", tokenizer"./model")gr.Interface.from_pipel…...

猫咪化身蒲公英,浮毛满屋乱飞,有哪些宠物空气净化器值得购买?
不掉毛的猫咪究竟是谁在养? 当初去朋友家玩,被猫咪捕获芳心,没多久自己也领养了一只。没想到啊,这就意味着要和猫毛纠缠一辈子了。平时白天上班不在家,它就在一边跑动一边掉毛,回到家我都能推断它的行动路…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
