算法工程师重生之第二十七天（合并区间 单调递增的数字 监控二叉树 总结）

参考文献 代码随想录

一、合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

• 1 <= intervals.length <= 104
• intervals[i].length == 2
• 0 <= starti <= endi <= 104

问题分析

        要合并，说明有新的数据生成，如果你存在元数组上， 那么就要删除重叠的那个几个，然后在添加新的，那么数组的长度会发生改变，那么很麻烦，所以使用新的一个数组，来存储。先排序，然后第一个排序，第二个运行（每个元素的第几个），尽可能的让重合的相邻。

class Solution(object):def merge(self, intervals):""":type intervals: List[List[int]]:rtype: List[List[int]]"""intervals = sorted(intervals, key = lambda x:x[0])result = []result.append(intervals[0])  # 第一个区间可以直接放入结果集中if len(intervals) == 1:return intervalsfor i in range(1, len(intervals)):if  result[-1][1] >= intervals[i][0]:  # 发现重叠区间# 合并区间，只需要更新结果集最后一个区间的右边界，因为根据排序，左边界已经是最小的result[-1][1] = max(result[-1][1], intervals[i][1])else:result.append(intervals[i])  # 区间不重叠return result

二、单调递增的数字

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回 小于或等于 n 的最大数字，且数字呈 单调递增 。

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

提示:

• 0 <= n <= 109

问题分析

                判断后一位如果比前面的小，那么就要修改，前面减1，后面为9，那问题来了，遍历顺序该如何呢，例如332，从前往后遍历，遍历到第二3和2比较式，那么前面减1,3变成2，2变成9，最后结果是329，很明显不满足，所以要重后往前遍历，注意不能遍历到0，因为比较的时候要有2位，然后要有一个标记的flag，初始化为数组的长度，为什么不可以初始化为0呢？因为这个flag的作用是标记从flag往后的元素都要变成9，那为什么要标记呢，因为有可能出现这种情况1000，如果你判断，立马修改的话，那么最后的结果变成900，不满足，所以要用标记，此时标记flag==1，所以从1到数组的最后都标记为9，这样最后的结果才是999，满足。

class Solution(object):def monotoneIncreasingDigits(self, N):# 将整数转换为字符串strNum = str(N)# flag用来标记赋值9从哪里开始# 设置为字符串长度，为了防止第二个for循环在flag没有被赋值的情况下执行flag = len(strNum)# 从右往左遍历字符串for i in range(len(strNum) - 1, 0, -1):# 如果当前字符比前一个字符小，说明需要修改前一个字符if strNum[i - 1] > strNum[i]:flag = i  # 更新flag的值，记录需要修改的位置# 将前一个字符减1，以保证递增性质strNum = strNum[:i - 1] + str(int(strNum[i - 1]) - 1) + strNum[i:]# 将flag位置及之后的字符都修改为9，以保证最大的递增数字for i in range(flag, len(strNum)):strNum = strNum[:i] + '9' + strNum[i + 1:]# 将最终的字符串转换回整数并返回return int(strNum)

三、监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

提示：

1. 给定树的节点数的范围是 [1, 1000]。
2. 每个节点的值都是 0。

问题分析

这道题目首先要想，如何放置，才能让摄像头最小的呢？

从题目中示例，其实可以得到启发，我们发现题目示例中的摄像头都没有放在叶子节点上！

这是很重要的一个线索，摄像头可以覆盖上中下三层，如果把摄像头放在叶子节点上，就浪费的一层的覆盖。

所以把摄像头放在叶子节点的父节点位置，才能充分利用摄像头的覆盖面积。

那么有同学可能问了，为什么不从头结点开始看起呢，为啥要从叶子节点看呢？

因为头结点放不放摄像头也就省下一个摄像头， 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。

所以我们要从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

局部最优推出全局最优，找不出反例，那么就按照贪心来！

此时，大体思路就是从低到上，先给叶子节点父节点放个摄像头，然后隔两个节点放一个摄像头，直至到二叉树头结点。

此时这道题目还有两个难点：

1. 二叉树的遍历
2. 如何隔两个节点放一个摄像头

#确定遍历顺序

在二叉树中如何从低向上推导呢？

可以使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了。

后序遍历代码如下：

int traversal(TreeNode* cur) {// 空节点，该节点有覆盖if (终止条件) return ;int left = traversal(cur->left);    // 左int right = traversal(cur->right);  // 右逻辑处理                            // 中return ;
}

注意在以上代码中我们取了左孩子的返回值，右孩子的返回值，即left 和 right， 以后推导中间节点的状态

#如何隔两个节点放一个摄像头

此时需要状态转移的公式，大家不要和动态的状态转移公式混到一起，本题状态转移没有择优的过程，就是单纯的状态转移！

来看看这个状态应该如何转移，先来看看每个节点可能有几种状态：

有如下三种：

• 该节点无覆盖
• 本节点有摄像头
• 本节点有覆盖

我们分别有三个数字来表示：

• 0：该节点无覆盖
• 1：本节点有摄像头
• 2：本节点有覆盖

大家应该找不出第四个节点的状态了。

一些同学可能会想有没有第四种状态：本节点无摄像头，其实无摄像头就是 无覆盖 或者 有覆盖的状态，所以一共还是三个状态。

因为在遍历树的过程中，就会遇到空节点，那么问题来了，空节点究竟是哪一种状态呢？ 空节点表示无覆盖？ 表示有摄像头？还是有覆盖呢？

回归本质，为了让摄像头数量最少，我们要尽量让叶子节点的父节点安装摄像头，这样才能摄像头的数量最少。

那么空节点不能是无覆盖的状态，这样叶子节点就要放摄像头了，空节点也不能是有摄像头的状态，这样叶子节点的父节点就没有必要放摄像头了，而是可以把摄像头放在叶子节点的爷爷节点上。

所以空节点的状态只能是有覆盖，这样就可以在叶子节点的父节点放摄像头了

接下来就是递推关系。

那么递归的终止条件应该是遇到了空节点，此时应该返回2（有覆盖），原因上面已经解释过了。

代码如下：

// 空节点，该节点有覆盖
if (cur == NULL) return 2;

递归的函数，以及终止条件已经确定了，再来看单层逻辑处理。

主要有如下四类情况：

• 情况1：左右节点都有覆盖

左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

如图：

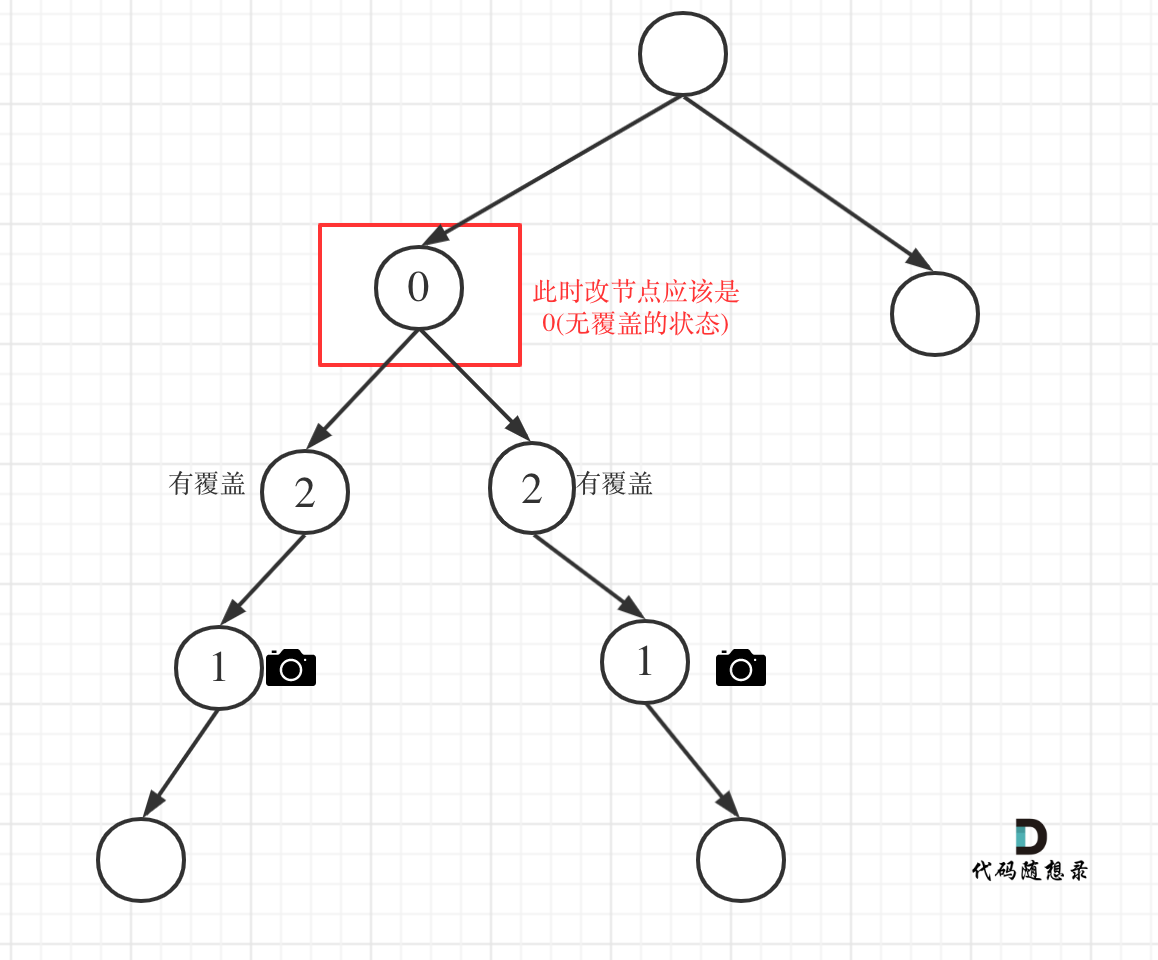
代码如下：

// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;

• 情况2：左右节点至少有一个无覆盖的情况

如果是以下情况，则中间节点（父节点）应该放摄像头：

• left == 0 && right == 0 左右节点无覆盖
• left == 1 && right == 0 左节点有摄像头，右节点无覆盖
• left == 0 && right == 1 左节点有无覆盖，右节点摄像头
• left == 0 && right == 2 左节点无覆盖，右节点覆盖
• left == 2 && right == 0 左节点覆盖，右节点无覆盖

这个不难理解，毕竟有一个孩子没有覆盖，父节点就应该放摄像头。

此时摄像头的数量要加一，并且return 1，代表中间节点放摄像头。

代码如下：

if (left == 0 || right == 0) {result++;return 1;
}

• 情况3：左右节点至少有一个有摄像头

如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

• left == 1 && right == 2 左节点有摄像头，右节点有覆盖
• left == 2 && right == 1 左节点有覆盖，右节点有摄像头
• left == 1 && right == 1 左右节点都有摄像头

代码如下：

if (left == 1 || right == 1) return 2;

1

从这个代码中，可以看出，如果left == 1, right == 0 怎么办？其实这种条件在情况2中已经判断过了，如图：

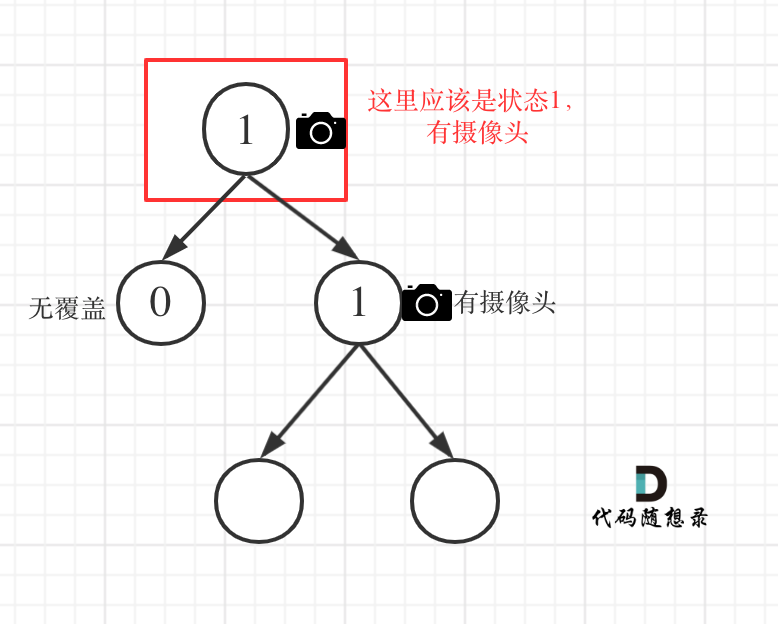
这种情况也是大多数同学容易迷惑的情况。

1. 情况4：头结点没有覆盖

以上都处理完了，递归结束之后，可能头结点 还有一个无覆盖的情况，如图：

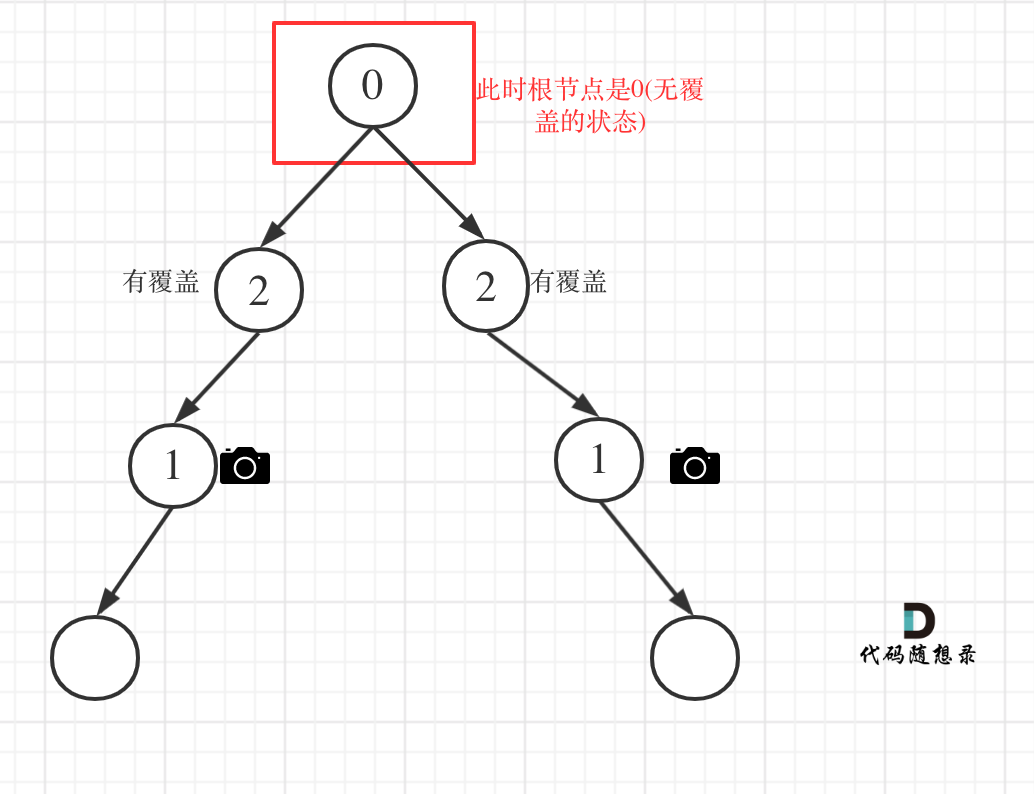
所以递归结束之后，还要判断根节点，如果没有覆盖，result++，代码如下：

int minCameraCover(TreeNode* root) {result = 0;if (traversal(root) == 0) { // root 无覆盖result++;}return result;
}

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:# Greedy Algo:# 从下往上安装摄像头：跳过leaves这样安装数量最少，局部最优 -> 全局最优# 先给leaves的父节点安装，然后每隔两层节点安装一个摄像头，直到Head# 0: 该节点未覆盖# 1: 该节点有摄像头# 2: 该节点有覆盖def minCameraCover(self, root: TreeNode) -> int:# 定义递归函数result = [0]  # 用于记录摄像头的安装数量if self.traversal(root, result) == 0:result[0] += 1return result[0]def traversal(self, cur: TreeNode, result: List[int]) -> int:if not cur:return 2left = self.traversal(cur.left, result)right = self.traversal(cur.right, result)# 情况1: 左右节点都有覆盖if left == 2 and right == 2:return 0# 情况2:# left == 0 && right == 0 左右节点无覆盖# left == 1 && right == 0 左节点有摄像头，右节点无覆盖# left == 0 && right == 1 左节点无覆盖，右节点有摄像头# left == 0 && right == 2 左节点无覆盖，右节点覆盖# left == 2 && right == 0 左节点覆盖，右节点无覆盖if left == 0 or right == 0:result[0] += 1return 1# 情况3:# left == 1 && right == 2 左节点有摄像头，右节点有覆盖# left == 2 && right == 1 左节点有覆盖，右节点有摄像头# left == 1 && right == 1 左右节点都有摄像头if left == 1 or right == 1:return 2

 四、贪心总结

贪心理论基础

在贪心系列开篇词关于贪心算法，你该了解这些！ (opens new window)中，我们就讲解了大家对贪心的普遍疑惑。

1. 贪心很简单，就是常识？

跟着一起刷题的录友们就会发现，贪心思路往往很巧妙，并不简单。

1. 贪心有没有固定的套路？

贪心无套路，也没有框架之类的，需要多看多练培养感觉才能想到贪心的思路。

1. 究竟什么题目是贪心呢？

Carl个人认为：如果找出局部最优并可以推出全局最优，就是贪心，如果局部最优都没找出来，就不是贪心，可能是单纯的模拟。（并不是权威解读，一家之辞哈）

但我们也不用过于强调什么题目是贪心，什么不是贪心，那就太学术了，毕竟学会解题就行了。

1. 如何知道局部最优推出全局最优，有数学证明么？

在做贪心题的过程中，如果再来一个数据证明，其实没有必要，手动模拟一下，如果找不出反例，就试试贪心。面试中，代码写出来跑过测试用例即可，或者自己能自圆其说理由就行了

就像是 要用一下 1 + 1 = 2，没有必要再证明一下 1 + 1 究竟为什么等于 2。（例子极端了点，但是这个道理）

相信大家读完关于贪心算法，你该了解这些！ (opens new window)，就对贪心有了一个基本的认识了。

#贪心简单题

以下三道题目就是简单题，大家会发现贪心感觉就是常识。是的，如下三道题目，就是靠常识，但我都具体分析了局部最优是什么，全局最优是什么，贪心也要贪的有理有据！

• 贪心算法：分发饼干(opens new window)
• 贪心算法：K次取反后最大化的数组和(opens new window)
• 贪心算法：柠檬水找零(opens new window)

#贪心中等题

贪心中等题，靠常识可能就有点想不出来了。开始初现贪心算法的难度与巧妙之处。

• 贪心算法：摆动序列(opens new window)
• 贪心算法：单调递增的数字(opens new window)

#贪心解决股票问题

大家都知道股票系列问题是动规的专长，其实用贪心也可以解决，而且还不止就这两道题目，但这两道比较典型，我就拿来单独说一说

• 贪心算法：买卖股票的最佳时机II(opens new window)
• 贪心算法：买卖股票的最佳时机含手续费 (opens new window)本题使用贪心算法比较绕，建议后面学习动态规划章节的时候，理解动规就好

#两个维度权衡问题

在出现两个维度相互影响的情况时，两边一起考虑一定会顾此失彼，要先确定一个维度，再确定另一个一个维度。

• 贪心算法：分发糖果(opens new window)
• 贪心算法：根据身高重建队列(opens new window)

在讲解本题的过程中，还强调了编程语言的重要性，模拟插队的时候，使用C++中的list（链表）替代了vector(动态数组)，效率会高很多。

所以在贪心算法：根据身高重建队列（续集） (opens new window)详细讲解了，为什么用list（链表）更快！

大家也要掌握自己所用的编程语言，理解其内部实现机制，这样才能写出高效的算法！

#贪心难题

这里的题目如果没有接触过，其实是很难想到的，甚至接触过，也一时想不出来，所以题目不要做一遍，要多练！

#贪心解决区间问题

关于区间问题，大家应该印象深刻，有一周我们专门讲解的区间问题，各种覆盖各种去重。

• 贪心算法：跳跃游戏(opens new window)
• 贪心算法：跳跃游戏II(opens new window)
• 贪心算法：用最少数量的箭引爆气球(opens new window)
• 贪心算法：无重叠区间(opens new window)
• 贪心算法：划分字母区间(opens new window)
• 贪心算法：合并区间(opens new window)

#其他难题

贪心算法：最大子序和 (opens new window)其实是动态规划的题目，但贪心性能更优，很多同学也是第一次发现贪心能比动规更优的题目。

贪心算法：加油站 (opens new window)可能以为是一道模拟题，但就算模拟其实也不简单，需要把while用的很娴熟。但其实是可以使用贪心给时间复杂度降低一个数量级。

最后贪心系列压轴题目贪心算法：我要监控二叉树！ (opens new window)，不仅贪心的思路不好想，而且需要对二叉树的操作特别娴熟，这就是典型的交叉类难题了。