Superset SQL模板使用
使用背景
有时想让表的时间索引生效,而不是在最外层配置报表时,再套多一层时间范围。这时可以使用SQL模板
参考官方文档
https://superset.apache.org/docs/configuration/sql-templating/#:~:text=SQL%20Lab%20and%20Explore%20supports%20Jinja
我的实践
1、定义一个dataset,其中我的dt是由外围dashboard的筛选项传进来的
select dt, team, sum(xx) xx
from t_test
where dt in ({{ "'" + "','".join(filter_values('dt')) + "'" }})
group by 1,2
为了防止保存dataset报错,你的dataset dt字段可以设置一个无效filter。比如我设置了no filter

2、dashboard定义filter。

保存后,superset会自动将用户选择的dt变量带进sql。生成的sql将是:
select dt, team, sum(xx) xx
from t_test
where dt in where dt in ('2024-10-07', 'No filter')
group by 1,2
这样便可以实现在内层让数据源使用索引
相关文章:

Superset SQL模板使用
使用背景 有时想让表的时间索引生效,而不是在最外层配置报表时,再套多一层时间范围。这时可以使用SQL模板 参考官方文档 https://superset.apache.org/docs/configuration/sql-templating/#:~:textSQL%20Lab%20and%20Explore%20supports%20Jinja 我…...
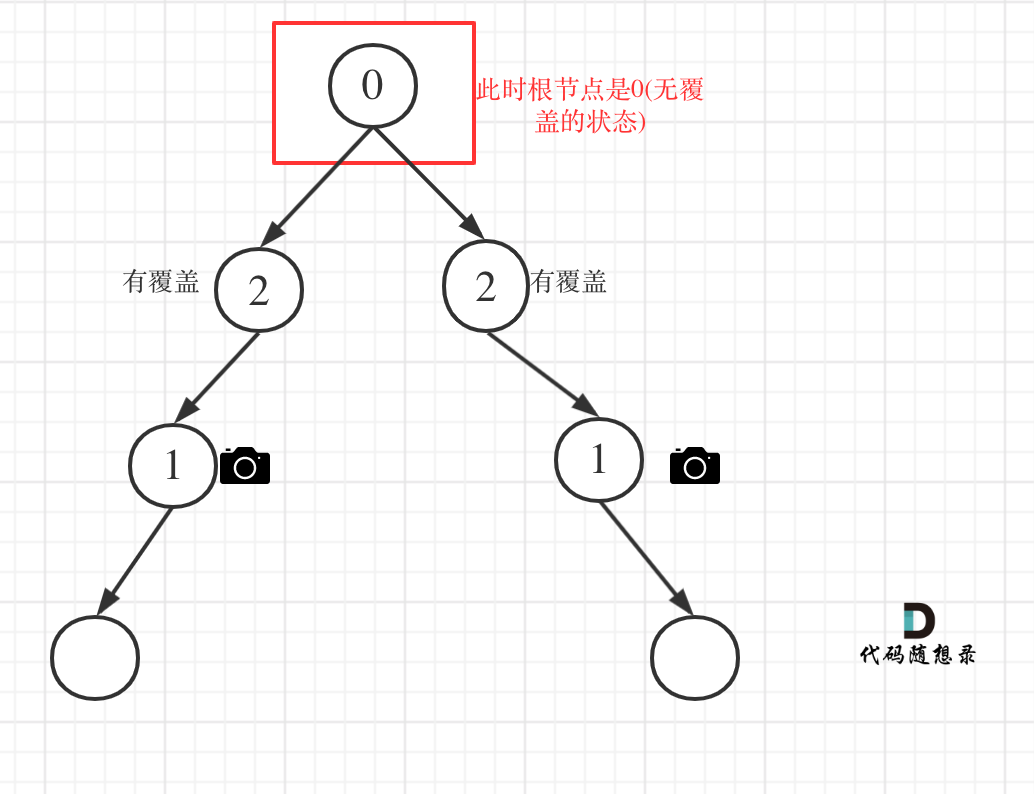
算法工程师重生之第二十七天(合并区间 单调递增的数字 监控二叉树 总结)
参考文献 代码随想录 一、合并区间 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 1:…...

前端开发基础NodeJS+NPM基本使用(零基础入门)
文章目录 1、Nodejs基础1.1、NodeJs简介1.2、下载安装文件1.3、安装NodeJS1.4、验证安装2、Node.js 创建第一个应用2.1、说明2.2、创建服务脚本2.3、执行运行代码2.4、测试访问3、npm 基本使用3.1、测试安装3.2、配置淘宝npm镜像3.3.1、本地安装3.3.2、全局安装3.4、查看安装信…...
)
深度学习 nd.random.normal()
nd.random.normal() 是 MXNet 中用于生成符合正态分布(高斯分布)随机数的函数。它允许用户指定均值、标准差以及生成的随机数的形状。 函数签名 mx.nd.random.normal(loc0.0, scale1.0, shape(1,)) 参数 loc: 生成的随机数的均值,默认为 …...

Redis Geo 数据类型解析:基于 ZSET 的高效地理位置管理0708
根据官网介绍: Bitmaps are not an actual data type, but a set of bit-oriented operations defined on the String type which is treated like a bit vector. Since strings are binary safe blobs and their maximum length is 512 MB, they are suitable to s…...
爬虫post收尾以及cookie加代理
爬虫post收尾以及cookie加代理 目录 1.post请求收尾 2.cookie加代理 post收尾 post请求传参有两种格式,载荷中有请求载荷和表单参数,我们需要做不同的处理。 1.表单数据:data字典传参 content-type: application/x-www-form-urlencoded; …...

c++STL——map与set的使用及介绍
目录 前言: 1. 关联式容器 2. 键值对 3. 树形结构的关联式容器 3.1 set 3.1.1 set的介绍 3.1.2 set的使用 1. set的模板参数列表 2. set的构造 3. set的迭代器 4. set的容量 5. set修改操作 6. set的使用举例 3.2 map 3.2.1 map的介绍 3.2.2 map的…...

Vxe UI vue vxe-table select 下拉框选项列表数据量超大过大时卡顿解决方法
Vxe UI vue vxe-table vxe-grid select 下拉框选项列表数据量超大过大时卡顿解决方法 查看 github vxe-table 官网 vxe-table 本身支持虚拟滚动,数据量大也是支持的,但是如果在可编辑表格中使用下拉框,下拉框的数据量超大时,可能…...

python 基础笔记(其实有点内容的)
print(math.gamma(n)) # 求 (n-1) 的阶乘 数值, 数值计算 format(50, “b”) bin(50)[2:], 这个“b” 就代表的是 binary format(14, ‘b’) ------> ‘1110’ 去除 0b 去掉前导零 str(000001) # 只适合python2.x ‘1’ “00000001”.lstrip(“0”) # python3…...

(39)MATLAB生成高斯脉冲及其频谱
文章目录 前言一、MATLAB仿真代码二、仿真结果画图 前言 高斯脉冲在通信中是很重要的调制符号波形,本文使用MATLAB生成高斯脉冲,并使用FFT变换给出其频谱。 一、MATLAB仿真代码 代码如下: % 信号参数 fs 100; % 采样…...

35岁前端开发者:转型还是坚守?
在互联网行业,35岁似乎成了一个敏感的年龄分水岭。很多前端开发者开始思考:到了35岁,是不是都要转型?本文将探讨这个话题,希望能为面临这一困惑的前端开发者提供一些参考。 一、35岁焦虑:现实还是误解&…...

对MVC详细解读
一、MVC模式的详细组成部分 1. 模型(Model) 数据结构: 模型通常使用类或结构来定义应用程序的数据结构。例如,在Ruby on Rails中,模型通常与数据库表相对应,使用Active Record模式。 数据访问层࿱…...
centos系列图形化 VNC server配置,及VNC viewer连接,2024年亲测有效
centos系列图形化 VNC server配置,及VNC viewer连接 0.VNC服务介绍 VNC英文全称为Virtual Network Computing,可以位操作系统提供图形接口连接方式,简单的来说就是一款桌面共享应用,类似于qq的远程连接。该服务是基于C/S模型的。…...

STL序列式容器之string的基本用法及实现
1.string类 在使用string类时,必须包含<string>头文件以及using namespace std; 接下来我们看看string类是如何被声明的: typedef basic_string<char> string; 可以看到:string类是被类模板basic_string用数据类型…...

lua脚本使用cjson转换json时,空数组[]变成了空对象{}
一、前言 项目lua使用工具:cjson 问题:reids中部分数据的json key存在为[]的值,使用cjson进行解析的时候将原本空数组[]解析成了空对象{} 目标:原本[] 转 [] 二、解决方案 在使用cjson类库时,先配置json转换要求 -…...

ImportError: /../lib/libstdc++.so.6: version `GLIBCXX_3.4.29解决方案
今天跑实验遇到了一个头疼的报错,完全看不懂,上网查了一下成功解决,但是网上的指令没法直接拿来用,所以在这里记录一下自己的解决方案。 报错信息: Traceback (most recent call last):File "/home/shizhiyuan/c…...

java-实现一个简单的httpserver-0.6.0
2024年10月14日14:17:07—0.6.0 java-实现一个简单的httpserver-0.6.0 背景功能具体代码打印 背景 通常写了一些接口,需要通过临时的http访问,又不需要spring这么厚重的框架 功能 设置并发监控并发两个get请求一个是根路径,一个是other增加…...

【论文#码率控制】ADAPTIVE RATE CONTROL FOR H.264
目录 摘要1.前言2.基本知识2.1 蛋鸡悖论2.2 基本单元的定义2.3 线性MAD预测模型 3.GOP级码率控制3.1 总比特数3.2 初始化量化参数 4.帧级码率控制4.1 非存储图像的量化参数4.2 存储图像的目标比特 5.基本单元级码率控制6.实验结果7.结论 《ADAPTIVE RATE CONTROL FOR H.264》 A…...

2024-10-16 学习人工智能的Day8
函数 定义(创建) 函数的创建def开始,后接函数名,在给参数表最后冒号表示函数基础信息给定 换行书写函数内部定义,在函数内部定义操作,最后函数自带返回,无定义返回值返回为None&…...

Python Django 数据库优化与性能调优
Python Django 数据库优化与性能调优 Django 是一个非常流行的 Python Web 框架,它的 ORM(对象关系映射)允许开发者以简单且直观的方式操作数据库。然而,随着数据量的增长,数据库操作的效率可能会成为瓶颈,…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
