算法.图论-BFS及其拓展
文章目录
- 广度优先搜索简介
- 经典bfs习题
- 地图分析
- 贴纸拼词
- 01bfs解析
- 基本过程
- 相关习题
广度优先搜索简介
-
bfs的特点是逐层扩散, 从源头到目标点扩散了几层, 最短路就是多少
-
bfs的使用特征是任意两个节点的距离(权值)是相同的(无向图, 矩阵天然满足这一特点)
-
bfs开始的时候可以是单个源头, 也可以多个源头(单源bfs, 和多源bfs)
-
bfs进出队列的时候可以是单点弹出, 也可以是整层弹出
如果是单点弹出的时候, 队列中存放的是当前的节点和距离源点的距离
整层弹出则不需要, 只需要保留一个level计数就可以知道到源点的距离
-
bfs进行时通常需要一个visit数组(一般是boolean[][])来标记已经遍历到的位置
-
bfs的时候一个点向四个方向遍历的时候通常可以用一个move数组搞定(下面是举例)
//建立一个全局的move数组来进行四个方向的遍历(上, 右, 下, 左) private static final int[] move = new int[]{-1, 0, 1, 0, -1}; //假设下面的函数是用来进行 (i, j) 的遍历的 private static void traversal(int i, int j, int[][] matrix, boolean[][] visit){//不用写四个if, 仅仅需要进行for循环四次就可以了int r = matrix.length;int c = matrix[0].length;for(int k = 0; k < 4; k++){int ni = i + move[k];int nj = j + move[k + 1];if(ni >= 0 && ni < r && nj >= 0 && nj < c && !visit[ni][nj]){//下一个位置不越界并且没有访问过//.....进行处理逻辑, 并最终把visit数组的这一个位置置为truevisit[ni][nj] = true;}} } -
bfs设计的时候有很多的剪枝的操作需要进行一定的摸索
经典bfs习题
地图分析
链接: leetcode1162.地图分析
题目简介:

解释一下什么是曼哈顿距离, 就是一个点到另外一个点的横坐标的差值和纵坐标的差值之和, 这与我们习惯认为的对角线距离区别开
这种距离的定义通常用于矩形的表格之中(实质上: bfs最广的应用就是矩形格之中, 因为这是一种天然的无向图)
这道题本质上是要找距离陆地最近的海洋的最远的距离, 翻译成人话就是寻找距离陆地最远的海洋, 那我们直接以陆地为源点开始进行bfs即可
我们下面给出来两种实现的方案
第一种是单点弹出的方法
//创建一个move数组private static final int[] move = new int[]{-1, 0, 1, 0, -1};//创建一个全局的visit数组private static final int MAXM = 101;private static final boolean[][] visit = new boolean[MAXM][MAXM];//方法一: 单点弹出的方式public int maxDistance(int[][] grid) {int r = grid.length;int c = grid[0].length;int seas = 0;Queue<int[]> q = new ArrayDeque<>();//遍历一下grid数组初始化队列元素同时初始化visit数组for(int i = 0; i < r; i++){for(int j = 0; j < c; j++){if(grid[i][j] == 1){visit[i][j] = true;q.offer(new int[]{i, j, 0});}else{visit[i][j] = false;seas++;}}}//特殊条件直接返回if(seas == r * c || seas == 0){return -1;}//进行bfs的主流程int distanse = 1;while(!q.isEmpty()){int[] cur = q.poll();//向四个方向尝试扩展for(int k = 0; k < 4; k++){int nx = cur[0] + move[k];int ny = cur[1] + move[k + 1];if(nx >= 0 && nx < r && ny >= 0 && ny < c && !visit[nx][ny]){visit[nx][ny] = true;q.offer(new int[]{nx, ny, cur[2] + 1});distanse = Math.max(distanse, cur[2] + 1);}}}return distanse;}
}
第二种就是整层弹出的方法
class Solution {//创建一个move数组private static final int[] move = new int[]{-1, 0, 1, 0, -1};//创建一个全局的visit数组private static final int MAXM = 101;private static final boolean[][] visit = new boolean[MAXM][MAXM];//方法二 : 整层弹出的方式public int maxDistance(int[][] grid) {int r = grid.length;int c = grid[0].length;int seas = 0;Queue<int[]> q = new ArrayDeque<>();//遍历一下grid数组初始化队列元素同时初始化visit数组for(int i = 0; i < r; i++){for(int j = 0; j < c; j++){if(grid[i][j] == 1){visit[i][j] = true;q.offer(new int[]{i, j});}else{visit[i][j] = false;seas++;}}}//特殊条件直接返回if(seas == r * c || seas == 0){return -1;}//进行bfs的主流程int level = 0;while(!q.isEmpty()){level++;int sz = q.size();while(sz-- != 0){int[] cur = q.poll();//尝试向四个方向扩展for(int k = 0; k < 4; k++){int nx = cur[0] + move[k];int ny = cur[1] + move[k + 1];if(nx >= 0 && nx < r && ny >= 0 && ny < c && !visit[nx][ny]){q.offer(new int[]{nx, ny});visit[nx][ny] = true;}}}}return level - 1;}
}
贴纸拼词
链接: [leetcode691.贴纸拼词](. - 力扣(LeetCode))
题目描述: 
这个题的解题思路就是, 对于目标字符串target, 我们想要使用最少的代价进行拼词,
这道题如何想到用bfs主要就是对于一个字符串
target, 我们提供的每一个词都有对应的一种展开, 如下图
图片:

从上面的演示过程也不难看出, 我们这个本题剪枝的关键就是对target的进行排序操作, 主要就是优先削减头部的字符
代码实现如下(重点在理解逻辑)
class Solution {public static int minStickers(String[] stickers, String target) {//首先对数组中的单词排序并进行词频统计List<int[]> times = new ArrayList<>();for(int i = 0; i < stickers.length; i++){int[] temp = new int[26];String changeStr = sort(stickers[i], temp);stickers[i] = changeStr;times.add(temp);}//排序一下target字符串int[] targetTime = new int[26];target = sort(target, targetTime);Queue<String> q = new ArrayDeque<>();HashSet<String> set = new HashSet<>();StringBuilder sp = new StringBuilder();//进行bfs的主流程q.offer(target);int level = 0;//本质上还是我们弹出的逻辑没有搞懂, 我们应该一层一层的弹出while(!q.isEmpty()){int sz = q.size();level++;while(sz-- != 0){int[] curTime = new int[26];String cur = q.poll();//统计一下当前的词频for(int i = 0; i < cur.length(); i++){curTime[cur.charAt(i) - 'a']++;}for(int i = 0; i < stickers.length; i++){if(times.get(i)[cur.charAt(0) - 'a'] != 0){String next = buildStr(curTime, times.get(i), sp);if(next.equals("")) return level;if(!set.contains(next)) {set.add(next);q.offer(next);}}}}}return -1;}//对字符串排序的方法, 顺便统计一下词频private static String sort(String s, int[] temp){char[] cs = s.toCharArray();for(char elem : cs){temp[elem - 'a']++;}Arrays.sort(cs);return String.valueOf(cs);}//生成一个新的字符串private static String buildStr(int[] curTime, int[] time, StringBuilder sp){sp.setLength(0);for(int i = 0; i < 26; i++){if(curTime[i] != 0){for(int j = 0; j < Math.max(curTime[i] - time[i], 0); j++){sp.append((char)(i + 'a'));}}}return sp.toString();}}
01bfs解析
基本过程
01bfs是一种特殊的bfs, 适用于01图找寻最短路径的情况, 01bfs时间复杂度是O(节点数量 + 边的数量) 下图是我们的实例
图片:

上面就是一个01bfs找寻最短路径的情况, 我们的解题的流程是固定的, 如下(正确性证明略), 主要就是双端队列结合bfs
-
创建一个distance表, 含义就是源点到i点的最短距离是多少
大小就是所有的节点位置, 初始化所有点的distance[i] = Integer.MAX_VALUE
-
将源点加入双端队列, 并修改distance[源点] = 0
-
当队列不为空的时候进入循环(下面就是伪代码)
while(!queue.isEmpty()){//弹出一个节点(弹出的时候一定从头部弹出)Node node = queue.poll();//如果这个位置就是要找的目标节点就直接返回if(node == targetNode) return distance[node];//找到这个节点去的下一个位置(可能有多个...)int next = node -> next;//weight就是这两个点之间的权值(0 or 1)int weight = 0 or 1; if(distance[node] + weight < distance[next]){//此时说明到达next的位置可以边的更小就更新distance[next] = distance[node] + weight;//然后在队列中加入这个位置, 如果刚才的权值weight == 0, 就从头部加入, 如果是1就从尾部加入if(weight == 0){queue.offerFirst(node);}else{queue.offerLast(node);}} }
相关习题
图片: 
链接: leetcode2290.到达角落的最小代价
其实就是01bfs的模板题
class Solution {//经典01dfs板子题private static final int[] move = new int[]{-1, 0, 1, 0, -1};public int minimumObstacles(int[][] grid) {int r = grid.length;int c = grid[0].length;//初始化一个distance数组int[][] distance = new int[r][c];for(int i = 0; i < r; i++){for(int j = 0; j < c; j++){distance[i][j] = Integer.MAX_VALUE;}}//创建一个双端队列Deque<int[]> dq = new ArrayDeque<>();dq.offer(new int[]{0, 0});distance[0][0] = 0;while(!dq.isEmpty()){int[] cur = dq.poll();//如果是目标节点if(cur[0] == r - 1 && cur[1] == c - 1) return distance[cur[0]][cur[1]];//尝试向四个方向扩展for(int k = 0; k < 4; k++){int nx = cur[0] + move[k];int ny = cur[1] + move[k + 1];if(nx >= 0 && nx < r && ny >= 0 && ny < c && distance[cur[0]][cur[1]] + grid[nx][ny] < distance[nx][ny]){distance[nx][ny] = distance[cur[0]][cur[1]] + grid[nx][ny];if(grid[nx][ny] == 0){dq.offerFirst(new int[]{nx, ny});}else{dq.offerLast(new int[]{nx, ny});}}}}return -1;}
rst(new int[]{nx, ny});}else{dq.offerLast(new int[]{nx, ny});}}}}return -1;}
}
链接: leetcode1368.箭头数组的最短代价
图片: 
class Solution {//这个move数组的设计是比较的精巧的private static final int[][] move = {{0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}};public int minCost(int[][] grid) {int r = grid.length;int c = grid[0].length;//初始化distance数组int[][] distance = new int[r][c];for(int i = 0; i < r; i++){Arrays.fill(distance[i], Integer.MAX_VALUE);}//创建双端队列Deque<int[]> dq = new ArrayDeque<>();dq.offer(new int[]{0, 0});distance[0][0] = 0;while(!dq.isEmpty()){int[] cur = dq.poll();int x = cur[0];int y = cur[1];if(x == r - 1 && y == c - 1) return distance[x][y];for(int i = 1; i < 5; i++){int nx = x + move[i][0];int ny = y + move[i][1];int weight = i == grid[x][y] ? 0 : 1;if(nx >= 0 && nx < r && ny >= 0 && ny < c && distance[x][y] + weight < distance[nx][ny]){distance[nx][ny] = distance[x][y] + weight;if(weight == 0){dq.offerFirst(new int[]{nx, ny});}else{dq.offerLast(new int[]{nx, ny});}}}}return -1;}
}
相关文章:

算法.图论-BFS及其拓展
文章目录 广度优先搜索简介经典bfs习题地图分析贴纸拼词 01bfs解析基本过程相关习题 广度优先搜索简介 bfs的特点是逐层扩散, 从源头到目标点扩散了几层, 最短路就是多少 bfs的使用特征是任意两个节点的距离(权值)是相同的(无向图, 矩阵天然满足这一特点) bfs开始的时候可以是…...

mongodb的相关关键字说明
以下是MongoDB中一些数据库相关的关键字说明: 1. 数据库(Database) 概念 数据库是MongoDB中数据存储的最高层级容器,类似于关系型数据库中的数据库概念。一个MongoDB服务器实例可以包含多个数据库,每个数据库可以有自…...
强化学习之DDPG算法
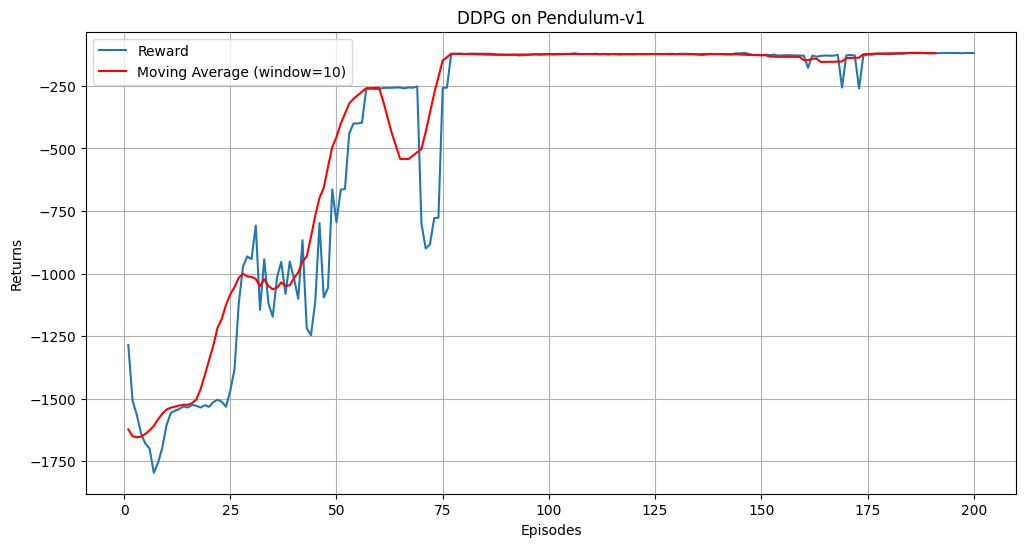
前言: 在正文开始之前,首先给大家介绍一个不错的人工智能学习教程:https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程,感兴趣的读者可以自行查阅。 一、算法介绍 深度确定性策略梯度 ࿰…...

【进阶OpenCV】 (16)-- 人脸识别 -- FisherFaces算法
文章目录 FisherFaces算法一、算法原理二、算法优势与局限三、算法实现1. 图像预处理2. 创建FisherFace人脸特征识别器3. 训练模型4. 测试图像 总结 FisherFaces算法 PCA方法是EigenFaces人脸识别的核心,但是其具有明显的缺点,在操作过程中会损失许多人…...

电脑主机配置
显卡: 查看显卡:设备管理器--显示适配器 RTX4060 RTX和GTX区别: GTX是NVIDIA公司旧款显卡,RTX比GTX好但是贵 处理器CPU: Intel(R) Core(TM) i5-10400F CPU 2.90GHz 2.90 GHz 10400F:10指的是第几代…...
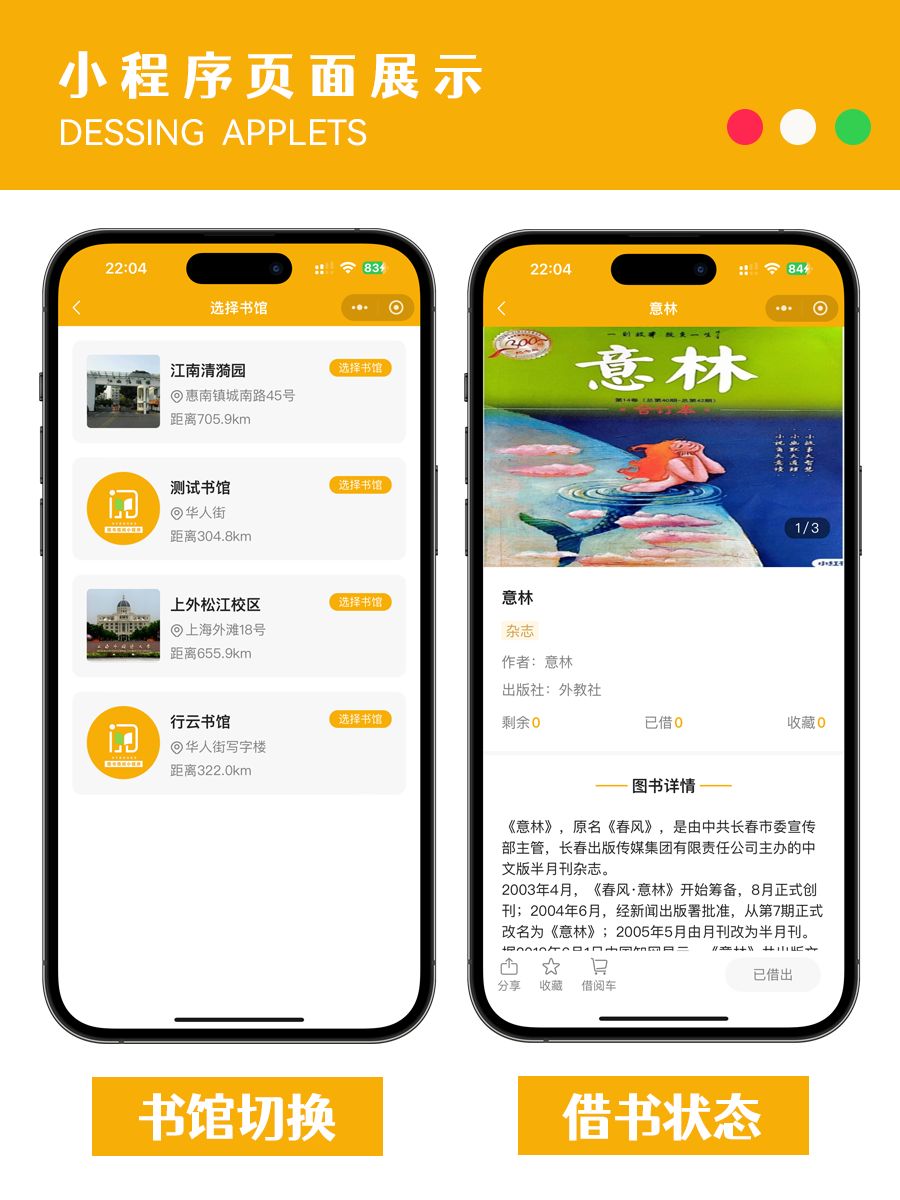
图书借阅小程序开源独立版
图书借阅微信小程序,多书馆切换模式,书馆一键同步图书信息,开通会员即可在线借书,一书一码书馆员工手机扫码出入库从会员到书馆每一步信息把控图书借阅小程序,让阅读触手可及在这个快节奏的时代,你是否渴望…...

flutter TextField限制中文,ios自带中文输入法变英文输入问题解决
由于业务需求,要限制TextField只能输入中文,但是测试在iOS测试机发现自带中文输入法会变英文输入问题,安卓没有问题,并且只有iOS自带输入法有问题,搜狗等输入法没问题。我们目前使用flutter2.5.3版本,高版本…...

ThreadLocal的应用场景
ThreadLocal介绍 ThreadLocal为每个线程都提供了变量的副本,使得每个线程访问各自独立的对象,这样就隔离了多个线程对数据的共享,使得线程安全。ThreadLocal有如下方法: 方法声明 描述public void set(T value)设置当前线程绑定的…...

Python--plt.errorbar学习笔记
plt.errorbar 是 Matplotlib 库中的一个函数,用于绘制带有误差条的图形。下面给出的代码行的详细解释: import numpy as np from scipy.special import kv, erfc from scipy.integrate import dblquad import matplotlib.pyplot as plt import scipy.in…...

文件信息类QFileInfo
常用方法: 构造函数 //参数:文件的绝对路径或相对路径 [explicit] QFileInfo::QFileInfo(const QString &path) 设置文件路径 可构造一个空的QFileInfo的对象,然后设置路径 //参数:文件的绝对路径或相对路径 void QFileI…...

堆排序(C++实现)
参考: 面试官:请写一个堆排序_哔哩哔哩_bilibiliC实现排序算法_c从小到大排序-CSDN博客 堆的基本概念 堆排实际上是利用堆的性质来进行排序。堆可以看做一颗完全二叉树。 堆分为两类: 最大堆(大顶堆):除根…...

Qt中加入UI文件
将 UI 文件整合到 Qt 项目 使用 Qt Designer 创建 UI 文件: 在 Qt Creator 中使用 Qt Designer 创建 UI 文件,设计所需的界面。确保在设计中包含所需的控件(如按钮、文本框等),并为每个控件设置明确的对象名称…...

Redisson使用全解
redisson使用全解——redisson官方文档注释(上篇)_redisson官网中文-CSDN博客 redisson使用全解——redisson官方文档注释(中篇)-CSDN博客 redisson使用全解——redisson官方文档注释(下篇)_redisson官网…...

Go4 和对 Go 的贡献
本篇内容是根据2017年4月份Go4 and Contributing to Go音频录制内容的整理与翻译, Brad Fitzpatrick 加入节目谈论成为开源 Go 的代言人、让社区参与 bug 分类、Go 的潜在未来以及其他有趣的 Go 项目和新闻。 过程中为符合中文惯用表达有适当删改, 版权归原作者所有. Erik St…...

区间动态规划
区间动态规划(Interval DP)是动态规划的一种重要变种,特别适用于解决一类具有区间性质的问题。典型的应用场景是给定一个区间,要求我们在满足某些条件下进行最优划分或合并。本文将从区间DP的基本思想、常见问题模型以及算法实现几…...

什么情况下需要使用电压探头
高压探头是一种专门设计用于测量高压电路或设备的探头,其作用是在电路测试和测量中提供安全、准确的信号捕获,并确保操作人员的安全。这些探头通常用于测量高压电源、变压器、电力系统、医疗设备以及其他需要处理高电压的设备或系统。 而高压差分探头差分…...
)
数据结构——八大排序(下)
数据结构中的八大排序算法是计算机科学领域经典的排序方法,它们各自具有不同的特点和适用场景。以下是这八大排序算法的详细介绍: 五、选择排序(Selection Sort) 核心思想:每一轮从未排序的元素中选择最小࿰…...

Linux系统:Ubuntu上安装Chrome浏览器
Ubuntu系统版本:23.04 在Ubuntu系统上安装Google Chrome浏览器,可以通过以下步骤进行: 终端输入以下命令,先更新软件源: sudo apt update 或 sudo apt upgrade终端输入以下命令,下载最新的Google Chrome .…...

Redis位图BitMap
一、为什么使用位图? 使用位图能有效实现 用户签到 等行为,用数据库表记录签到,将占用很多存储;但使用 位图BitMap,就能 大大减少存储占用 二、关于位图 本质上是String类型,最小长度8位(一个字…...

YOLOv11改进策略【卷积层】| ParNet 即插即用模块 二次创新C3k2
一、本文介绍 本文记录的是利用ParNet中的基础模块优化YOLOv11的目标检测网络模型。 ParNet block是一个即插即用模块,能够在不增加深度的情况下增加感受野,更好地处理图像中的不同尺度特征,有助于网络对输入数据更全面地理解和学习,从而提升网络的特征提取能力和分类性能…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
