数据结构 —— 树和二叉树简介
目录
0.前言
1.树的认识
什么是树
树的相关概念
树的表示
孩子兄弟表示法
2.二叉树的认识
什么是二叉树
特殊的二叉树
满二叉树
完全二叉树
二叉树的性质
性质一
性质二
性质三
二叉树的存储
顺序存储
链式存储
0.前言
笔者我之前讲解的数据结构都是线性的数据结构,比如:顺序表、链表、栈、队列。线性结构中存储的元素在逻辑上像是被一条线串起来的一样。现在我将介绍一种非线性的数据结构 —— 二叉树,但是介绍二叉树之前需要介绍一下树,因为二叉树是树的一种特殊情况。
1.树的认识
什么是树
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。之所以把它叫做树,是因为这种数据结构看起来像一棵倒过来的树,根朝上,叶朝下,如下图所示。

- 从上往下的第一个结点叫做根结点。
- 除根节点外,其余结点被分成m (m>0) 个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i<= m) 又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继。

注意:树形结构中,子树之间不能有交集,否则就不是树!变成了另一种数据结构 —— 图。
这就不是一棵树:
树的相关概念

- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
树的表示
表示一棵树说的就是用代码如何表示一棵树。前面列出的图都是树的逻辑图,也就是说,在逻辑上,我们希望他是这样的。表示树的时候,既要保存值域,也要保存结点和结点之间的关系,基于这点,实现起来是比较麻烦的,但是有人发明了如下几种表示树的方式。
- 双亲表示法:每个结点都记录自己的双亲。
- 孩子表示法:每个结点都记录自己的孩子。
- 孩子双亲表示法:每个结点既记录自己的孩子,也记录自己的双亲。
- 孩子兄弟表示法:每个结点既记录自己的孩子,也记录自己的兄弟。
其中最常用的是孩子兄弟表示法。
孩子兄弟表示法
孩子兄弟表示法说的就是,每个结点记录从左往右数的第一个孩子结点和自己后面的第一个兄弟结点。
每个结点的定义如下:

逻辑图如下:

2.二叉树的认识
什么是二叉树
二叉树是一种特殊的树,特殊的地方就在于二叉树每个结点的度最大为二。一棵二叉树是结点的一个有限集合,该集合必须具有以下条件之一:
- 或者为空。
- 或者由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
二叉树的逻辑图如下所示:

特殊的二叉树
在所有的二叉树中,有那么两种特殊的二叉树满二叉树和完全二叉树。
满二叉树
每一层结点都达到最大值的二叉树就是满二叉树。
如下图所示:

对于满二叉树而言,一个具有k层的满二叉树的结点个数为2^k-1个。
完全二叉树
完全二叉树是由满二叉树引申出来的,当一棵高度为k的二叉树的所有结点都能连续地、和高度为k的满二叉树中的节点一 一对应,这棵树就是完全二叉树。
- 满二叉树是一种特殊的完全二叉树。

二叉树的性质
性质一
对任何一棵二叉树,如果度为0其叶结点个数为n0,度为2的分支结点个数为n2,则有 n0 = n2+1。
性质二
若规定根结点的层数为第 1 层:
- 则一棵非空二叉树的第 i 层上最多有2^(i-1)个结点。
- 则深度为 h 的二叉树的最大结点数是2^h-1。
- 若规定根节点的层数为第1层,具有n个结点的满二叉树的深度为h。

性质三
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为 i 的结点有以下结论:
- 若 i > 0,序号为 i 的结点的双亲结点的编号为 (i-1) / 2。(若i==0,i为根结点,无双亲结点)
- 若2*i+1 < n,左孩子序号为2*i+1;若2*i+1 >= n,则无左孩子。
- 若2*i+2 < n,右孩子序号为2*i+2;若2*i+2 >= n,则无右孩子。

二叉树的存储
对于二叉树,一般可以使用两种存储结构来存储,分别是顺序存储结构和链式存储结构。
顺序存储
二叉树顺序存储指的是使用顺序结构存储二叉树,其实就是使用数组存储;具体做法是对二叉树的每个结点从0开始编号,数据存储在和编号一致的数组下标空间上。
上述性质三其实就是二叉树顺序存储的性质。
使用数组存储二叉树的时候,数据构成的集合在逻辑上是二叉树,物理空间上使用的是数组存储。
完全二叉树顺序存储示意图:

使用数组存储二叉树有个很明显的缺点就是,当存储的二叉树不是完全二叉树的时候,会有空间的浪费,并且这种浪费是不能避免的。
非完全二叉树顺序存储示意图:

所以:使用数组存储二叉树的时候,只适合存储完全二叉树。
在实际应用中,只有堆才会使用数组存储二叉树,后面讲解。
链式存储
二叉树链式存储指的是用链表来存储二叉树。具体的做法是链表中每个结点由3个域组成,数据域和左右指针域,左右指针域分别用来存储左孩子的地址和右孩子的地址。
二叉树结点表示:

二叉树链式存储结构示意图:

相关文章:

数据结构 —— 树和二叉树简介
目录 0.前言 1.树的认识 什么是树 树的相关概念 树的表示 孩子兄弟表示法 2.二叉树的认识 什么是二叉树 特殊的二叉树 满二叉树 完全二叉树 二叉树的性质 性质一 性质二 性质三 二叉树的存储 顺序存储 链式存储 0.前言 笔者我之前讲解的数据结构都是线性…...

ubuntu安装boost
下载官方安装包官方,我使用的是boost_1_86_0.zip版本 1、解压安装包 2、进入boost_1_86_0 3、./bootstrap.sh --prefix/path/ 4、./b2 5、sudo ./b2 install 6、~/.bashrc配置环境...

【Spring AI】Java实现类似langchain的第三方函数调用_原理与详细示例
Spring AI 介绍 :简化Java AI开发的统一接口解决方案 在过去,使用Java开发AI应用时面临的主要困境是没有统一且标准的封装库,导致开发者需要针对不同的AI服务提供商分别学习和对接各自的API,这增加了开发难度与迁移成本。而Sprin…...

CIM系统:智慧城市的数字基石
计算机集成制造系统(CIM)是智慧城市建设中的关键技术,它通过集成多种信息技术,为城市提供一个全面的数字化镜像。CIM系统不仅涉及建筑信息模型(BIM)、地理信息系统(GIS)、物联网&…...

Android中Fragment的使用场景与生命周期
Android中Fragment的使用场景和生命周期 在Android应用开发中,Fragment是一个非常重要的概念,它允许开发者将Activity拆分成多个可重用的UI组件,从而提供灵活的UI设计,简化Activity的复杂性,并适应不同的屏幕尺寸和方…...

输入网址后,浏览器是如何高效渲染出网页的?
当你打开浏览器,输入一个网址并按下回车,接下来发生的一切仿佛都在瞬间完成——网页很快加载出来,内容、图片、动画一应俱全,像魔法一样。然而,这背后却是一个复杂而高效的协作过程,涉及到浏览器内核的多个组件共同工作,特别是渲染线程的协调作用。那么,浏览器究竟是如…...

springboot单文件,多文件下载方式
简单大文件下载: /*** 下载大文件* param path 路径* param fileName 文件名* return* throws IOException*/ public static ResponseEntity<InputStreamResource> downloadFile(String path, String fileName) throws IOException {Path filePath Paths.ge…...
JIT详解
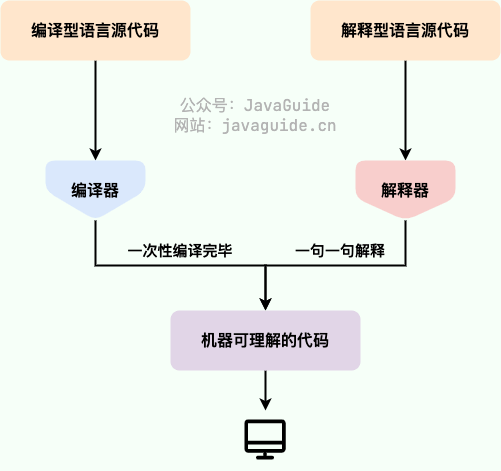
文章目录 JIT为什么说 Java 语言“编译与解释并存”? JIT原理JVM 架构简览JIT 编译流程JIT 编译器的实现优化策略方法内联逃逸分析 JIT 在Java中,JIT(Just-In-Time)编译器是Java虚拟机(JVM)的一个重要组成…...

线下陪玩导游系统软件源码,家政预约服务源码(h5+小程序+app)
游戏陪玩系统源码陪玩小程序源码搭建基于PHP+MySQL陪玩系统app源码陪玩系统定制开发服务、成品陪玩系统源码 系统基于Nginx或者Apache PHP7.3 数据库mysql5.6 前端为uniapp-vue2.0 后端为thinkphp6 有域名授权加密,其他开源可二开 演示源码下载 开…...

模拟退火算法最常见知识点详解与原理简介控制策略
章节目录 模拟退火算法简介与原理 算法的基本流程与步骤 关键参数与控制策略 模拟退火算法的应用领域 如何学习模拟退火算法 资源简介与总结 一、模拟退火算法简介与原理 重点详细内容知识点总结 1. 模拟退火算法简介 模拟退火算法(Simulated Annealing, SA&#x…...

C语言高效内存管理:对齐、缓存与位域
C语言高效内存管理:对齐、缓存与位域 一、内存对齐 1. 内存对齐的概念 内存对齐(Memory Alignment)是指数据在内存中存储时,其起始地址遵循特定的规则,使得数据能够被高效地访问。CPU通常以固定的字节数(…...

ES操作指南
# Creating a text file with the described Elasticsearch operations. es_operations """ Elasticsearch 基本操作语法: 1. 索引文档 (Index Documents): 自动生成 ID: POST /index_name/_doc { "field1": "value1", "…...

【黑苹果】记录MacOS升级Sonoma的过程
【黑苹果】记录MacOS升级Sonoma的过程 一、硬件二、提前说明三、准备OC四、选择驱动五、选择ACPI六、下载内核扩展七、其他问题 一、硬件 设备是神舟zx6-ct5da 具体参照下图 二、提前说明 本机器已经安装过 macOS Monterey 12.6,这次是升级到 macOS Sonoma 14。 …...
向“新”发力,朝“质”攀峰 | 资福医疗携手大圣胃肠一体内窥镜系统亮相江苏省医学会第八次健康管理学学术会议
伴随“健康中国”战略的深入实施,为进一步加强健康管理学科内涵建设,提升健康管理服务能力,促进健康管理学科创新及多部门、多产业交叉融合,2024年10月12~14日“江苏省医学会第八次健康管理学学术会议”在南京顺利召开…...

springboot项目多个数据源配置 dblink
当项目中涉及到多个数据库连接的时候该如何处理? 在对应的配置文件,配置对应的数据库情况,不过我确实没咋测试对于事务的处理我可以后续在多做测试 配置文件中配置对应的数据源 然后再使用的时候使用这个 DS(“pd_ob”)注解。 然后又长知识…...
介绍)
leetcode中哈希的python解法:Counter()介绍
Counter 是 Python 的 collections 模块中的一个类,用于统计可迭代对象中元素的出现次数。Counter 是一种专门为计数设计的哈希表(字典),它的键是元素,值是元素出现的次数。 Counter 的特点: 继承自 dict…...

VAS1800Q奇力科技线性芯片电荷泵热处理AEC-Q1000
VAS1800Q是一款专为汽车应用设计的高效恒流LED驱动器。它具备多个显著特点,不仅提升了LED驱动效率,还大大减少了热量的产生,使其在汽车照明领域中具有极高的应用价值。本文将详细介绍VAS1800Q的技术参数、功能及其在实际应用中的优势。 主要…...
 方法与 Stream API 查找枚举对象)
Java 枚举的 valueOf() 方法与 Stream API 查找枚举对象
文章目录 一、枚举类型概述二、valueOf() 方法详解1. 什么是 valueOf() 方法?2. 使用示例 三、使用 Stream API 查找枚举对象1. 使用 Stream 查找枚举对象2. 使用 Stream 统计枚举对象 四、总结推荐阅读文章 在 Java 中,枚举(enum)…...

Git的认识及基本操作
目录 一:Git的基本认识 二:Git的安装 三:Git的基本操作 1.创建本地仓库 2.配置Git 3.⼯作区、暂存区、版本库 4. 修改文件 5.版本回退 6.撤销修改 7.删除文件 一:Git的基本认识 1.实例引入 在日常当中我们常常会遇到这样的事,就是在做实验报告或者课设…...
python 日志库loguru
python 日志库loguru 安装 pip install loguru最简单的基本使用 from loguru import loggerlogger.success("Hello from success!") logger.info("Hello from info!") logger.debug("Hello from debug!") logger.warning("Hello from wa…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

