【Codeforces】CF 2009 F
Firefly’s Queries
#前缀和 #数据结构 #数学
题目描述
Firefly is given an array a a a of length n n n. Let c i c_i ci denote the i i i’th cyclic shift ∗ ^{\text{∗}} ∗ of a a a. She creates a new array b b b such that b = c 1 + c 2 + ⋯ + c n b = c_1 + c_2 + \dots + c_n b=c1+c2+⋯+cn where + + + represents concatenation † ^{\text{†}} †.
Then, she asks you q q q queries. For each query, output the sum of all elements in the subarray of b b b that starts from the l l l-th element and ends at the r r r-th element, inclusive of both ends.
∗ ^{\text{∗}} ∗The x x x-th ( 1 ≤ x ≤ n 1 \leq x \leq n 1≤x≤n) cyclic shift of the array a a a is a x , a x + 1 … a n , a 1 , a 2 … a x − 1 a_x, a_{x+1} \ldots a_n, a_1, a_2 \ldots a_{x - 1} ax,ax+1…an,a1,a2…ax−1. Note that the 1 1 1-st shift is the initial a a a.
† ^{\text{†}} †The concatenation of two arrays p p p and q q q of length n n n (in other words, p + q p + q p+q) is p 1 , p 2 , . . . , p n , q 1 , q 2 , . . . , q n p_1, p_2, ..., p_n, q_1, q_2, ..., q_n p1,p2,...,pn,q1,q2,...,qn.
输入格式
The first line contains t t t ( 1 ≤ t ≤ 1 0 4 1 \leq t \leq 10^4 1≤t≤104) — the number of test cases.
The first line of each test case contains two integers n n n and q q q ( 1 ≤ n , q ≤ 2 ⋅ 1 0 5 1 \leq n, q \leq 2 \cdot 10^5 1≤n,q≤2⋅105) — the length of the array and the number of queries.
The following line contains n n n integers a 1 , a 2 , . . . , a n a_1, a_2, ..., a_n a1,a2,...,an ( 1 ≤ a i ≤ 1 0 6 1 \leq a_i \leq 10^6 1≤ai≤106).
The following q q q lines contain two integers l l l and r r r ( 1 ≤ l ≤ r ≤ n 2 1 \leq l \leq r \leq n^2 1≤l≤r≤n2) — the left and right bounds of the query.
Note that the large inputs may require the use of 64-bit integers.
It is guaranteed that the sum of n n n does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105 and the sum of q q q does not exceed 2 ⋅ 1 0 5 2 \cdot 10^5 2⋅105.
输出格式
For each query, output the answer on a new line.
样例 #1
样例输入 #1
5
3 3
1 2 3
1 9
3 5
8 8
5 5
4 8 3 2 4
1 14
3 7
7 10
2 11
1 25
1 1
6
1 1
5 7
3 1 6 10 4
3 21
6 17
2 2
1 5
1 14
9 15
12 13
5 3
4 9 10 10 1
20 25
3 11
20 22
样例输出 #1
18
8
1
55
20
13
41
105
6
96
62
1
24
71
31
14
44
65
15解法
解题思路
可以发现,每次移动会改变相对位置,但是不会改变大小之和,而相对位置其实就是一个环。
我们可以把数组复制一遍变成环,化环为链,计算一遍前缀和。
而每次询问相当于询问固定的几个环,加上一个不完整的环,这个不完整的环就可以使用之前计算的前缀和来完成。
代码
void solve() {int n,q;cin >> n >> q;vector<int>a(n + 1), prefix(2 * n + 1);for (int i = 1; i <= n; ++i) {cin >> a[i];prefix[i] = prefix[i - 1] + a[i];}int s = prefix[n];for (int i = 1; i <= n; ++i) {prefix[n + i] = prefix[n + i - 1] + a[i];}auto cal = [&](int r)->int{int len = r / n, x = r % n;int L = len + 1, R = L + x - 1;int sum = len * s + prefix[R] - prefix[L - 1];return sum;};while (q--) {int l, r;cin >> l >> r;int res = cal(r);res -= cal(l-1);std::cout << res << "\n";}
}signed main() {ios::sync_with_stdio(0);std::cin.tie(0);std::cout.tie(0);int t = 1;cin >> t;while (t--) {solve();}
};
相关文章:

【Codeforces】CF 2009 F
Firefly’s Queries #前缀和 #数据结构 #数学 题目描述 Firefly is given an array a a a of length n n n. Let c i c_i ci denote the i i i’th cyclic shift ∗ ^{\text{∗}} ∗ of a a a. She creates a new array b b b such that b c 1 c 2 ⋯ c n b c…...

GTP4聊天记录中letax保存为word
别的不说,GPT4用来看代码很是很爽的,可以让他直接恢复出函数中的数学公式,有的时候为了做笔记,GPT4回复的答案,复制出来使markdown、letax等格式,为了更好的记笔记,可以使用下面的工具将复制…...

vscode调试编译找不到gcc,只有cl,但是检查cmd是对的,控制面板的路径也更改了
🏆本文收录于《全栈Bug调优(实战版)》专栏,主要记录项目实战过程中所遇到的Bug或因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&am…...

空间解析几何5-空间圆到平面的距离【附MATLAB代码】
目录 理论公式 matlab代码 理论公式 matlab代码 function [dis,P,Q,L]Circle2PlaneDistance(T,R,n,Pn) % output % dis 为最短距离,P为距离最短时圆上的点 Q为P对应的投影点 L为最小值有几个 % input % T为园心到基坐标系的变换矩阵 R为圆半径 n为平面的单位法向…...

[已解决] pycharm添加本地conda虚拟环境 + 配置解释器 - pycharm找不到conda可执行文件
目录 问题: 方法: 补充:创建conda虚拟环境 参考文档:pycharm找不到conda可执行文件怎么办?-CSDN 问题: 1.显示:未为项目配置 Python 解释器 2.想在pycharm中使用本地创建的虚拟环境 方法&a…...

SENT - Single Edge Nibble Transmission for Automotive
SENT 总线的特征和优势 SENT 总线是一种数字信号传输协议,具有更高的传输精度和速度;SENT 总线是单线传输数据,减少信号线,降低成本。加上电源和地线,总共 3 线;SENT 总线具有更强大的诊断功能;…...

2024年软件设计师中级(软考中级)详细笔记【7】面向对象技术(下)23种设计模式(分值10+)
目录 前言阅读前必看 第七章 面向对象技术(下)7.3 设计模式(固定4分)7.3.1 设计模式的要素7.3.2 创建型设计模式7.3.2.1 Abstract Factory(抽象工厂)7.3.2.2 Builder(生成器)7.3.2.3…...

未来人工智能的发展对就业市场的影响 人工智能在生活中的相关
人工智能(Artificial Intelligence),英文缩写为AI.是新一轮科技革命和产业变革的重要驱动力量, 是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学. 人工智能的发展对就业市场的影响主要…...

Oracle EBS 中财务模块
Oracle E-Business Suite (EBS) 提供了全面的财务管理解决方案,涵盖了企业财务活动的各个方面。以下是EBS中主要的财务模块及其功能概述: 总账(General Ledger, GL):Oracle EBS 中 GL 模块的财务流程概览-CSDN博客 总账…...
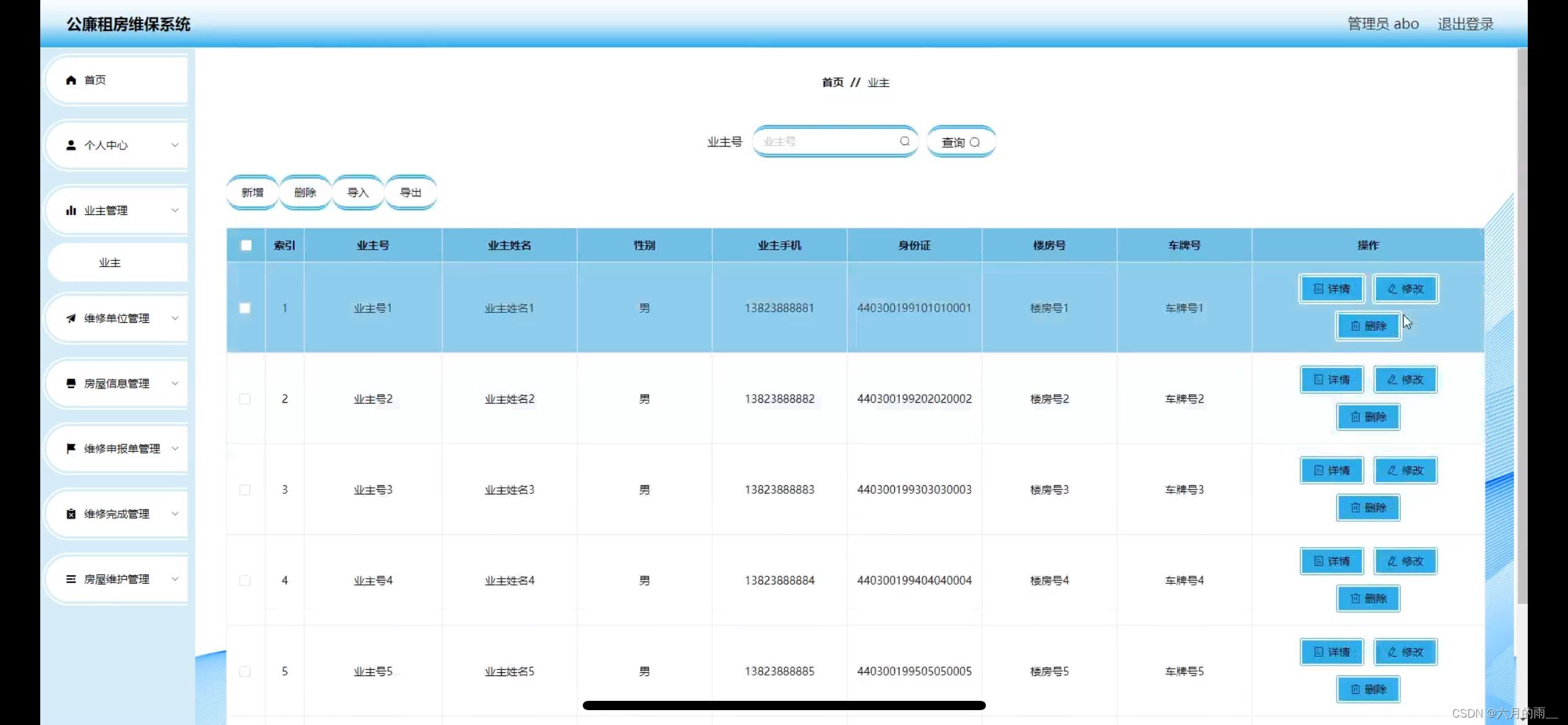
基于SSM公廉租房维保系统的设计
管理员账户功能包括:系统首页,个人中心,业主管理,维修单位管理,房屋信息管理,维修申报管理,维修完成,房屋维护管理 业主账号功能包括:系统首页,个人中心&…...

【AI大模型】深入Transformer架构:解码器部分的实现与解析
目录 🍔 解码器介绍 🍔 解码器层 2.1 解码器层的作用 2.2 解码器层的代码实现 2.3 解码器层总结 🍔 解码器 3.1 解码器的作用 3.2 解码器的代码分析 3.3 解码器总结 学习目标 🍀 了解解码器中各个组成部分的作用. &#…...

前端html js css 基础巩固3
一个这样的首页 滑动显示 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title>&l…...

如在下载自己的需要的rmp包呢
下载地址:https://pkgs.org/和https://rpmfind.net/linux/rpm2html/search.php 根基自己的需要进行下载使用。...

Android TextView实现一串文字特定几个字改变颜色
遇到一个需求,让Android端实现给定一个字符串指定下标的几个字颜色与其他字颜色不一致。 主要是用ForegroundColorSpan这个API来传入颜色值,用SpannableString来设置指定索引下标的字的颜色值。 这里通过给定一个输入文字描述框,要求输入指定…...

桃子叶片病害分类检测数据集(猫脸码客 第221期)
桃子叶片病害分类检测数据集 一、引言 桃子作为世界上广泛种植的果树之一,其叶片的健康状况直接关系到果实的产量和品质。然而,桃子叶片易受多种病害的侵袭,这些病害不仅影响叶片的光合作用,还可能导致果实减产、品质下降&#…...

Vue--》掌握自定义依赖引入的最佳实践
在现代前端开发中,vue凭借其灵活性和高效性,已成为开发者们的宠儿,然而随着项目的复杂度提升,如何高效地管理和引入依赖,尤其是自定义引入依赖,成为了许多开发者面临的一大挑战。无论是为了优化加载速度&am…...
)
repo 命令大全详解(第十四篇 repo overview)
repo overview 命令用于显示当前项目的概览信息,帮助用户快速了解项目的状态和分支信息。 参数分类及解释 基本参数 [--current-branch]: 可选,仅考虑已检出的分支。 示例: repo overview --current-branch [<project>...]: 可选,指定…...

【设计模式】深入理解Python中的抽象工厂设计模式
深入理解Python中的抽象工厂设计模式 设计模式是软件开发中解决常见问题的经典方案,而**抽象工厂模式(Abstract Factory Pattern)**是其中非常重要的一种创建型模式。抽象工厂模式的主要作用是提供一个接口,创建一系列相关或依赖…...

网站建设完成后,多久需要升级迭代一次
网站建设完成后,一般每隔几个月就会进行一次迭代升级。以下是关于网站迭代周期和原因的具体分析: 更新频率:网站在建设完成后,一般每隔几个月就会进行一次迭代升级。这种周期性的更新有助于保持网站的现代感和竞争力。更新目的&a…...

一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字
这里写目录标题 问题详情分析问题代码展示 问题详情 剑指 Offer 56: 一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。 示例: 输入&a…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

java+webstock
maven依赖 <dependency><groupId>org.java-websocket</groupId><artifactId>Java-WebSocket</artifactId><version>1.3.5</version></dependency><dependency><groupId>org.apache.tomcat.websocket</groupId&…...

项目研究:使用 LangGraph 构建智能客服代理
概述 本教程展示了如何使用 LangGraph 构建一个智能客服代理。LangGraph 是一个强大的工具,可用于构建复杂的语言模型工作流。该代理可以自动分类用户问题、分析情绪,并根据需要生成回应或升级处理。 背景动机 在当今节奏飞快的商业环境中,…...

全面解析网络端口:概念、分类与安全应用
在计算机网络的世界里,数据的传输与交互如同一场繁忙的物流运输,而网络端口就是其中不可或缺的 “货运码头”。无论是日常浏览网页、收发邮件,还是运行各类网络服务,都离不开网络端口的参与。本文将深入介绍网络端口的相关知识&am…...

Spring AOP执行原理源码解析
对【com.example.demo.TestAspect#aopTest】连接点增加了五个通知 在调用【com.example.demo.A#testAop()】(用户自定义)方法时,Cglib拦截器对其进行了拦截 可以看到执行顺序分别是环绕前置,前置,环绕后置,…...
