线性代数基础02
目录
1.向量
1.1向量的定义
1.2向量的运算
1.2.1向量加法
1.2.2向量数乘
1.2.3向量点积
1.3矩阵的特征值和特征向量
1.4向量的模
1.4.1向量的模的定义
1.4.2向量的模的几何解释
1.4.3向量的模的性质
1.5向量的内积
1.5.1向量的内积的定义
1.5.2向量的内积的几何解释
1.5.3向量的内积的性质
1.向量
1.1向量的定义
向量可以用多种方式定义,以下是几种常见的定义:
-
几何定义:向量是一个有方向和大小的量,通常用箭头表示。向量的起点称为原点,终点称为向量的端点。
-
代数定义:向量是一个有序的数组,通常表示为列向量或行向量。
例如,一个 n 维列向量可以表示为:

一个 n 维行向量可以表示为:
![]()
其中 v1,v2,…,vn是向量的分量。
行向量和列向量再本质上没有区别。
向量的表示
向量可以用多种方式表示,以下是几种常见的表示方法:
-
几何表示:在二维或三维空间中,向量通常用箭头表示,箭头的方向表示向量的方向,箭头的长度表示向量的大小。
-
代数表示:向量可以用列向量或行向量表示,如上所述。
-
坐标表示:在二维或三维空间中,向量可以用坐标表示。例如,二维向量 v=(v1,v2)v=(v1,v2) 表示在 x 轴和 y轴上的分量。
1.2向量的运算
向量有几种基本的运算,包括加法、数乘、点积和叉积。
1.2.1向量加法
向量加法是将两个向量的对应分量相加,得到一个新的向量。例如,两个 n 维向量 u 和 v 的加法为:

1.2.2向量数乘
向量数乘是将一个向量的每个分量乘以一个标量,得到一个新的向量。例如,一个 n 维向量 v 与标量 k 的数乘为:

1.2.3向量点积
向量点积(内积)是将两个向量的对应分量相乘,然后将结果相加,得到一个标量。例如,两个 n 维向量 u 和 v 的点积为:
![]()

1.3矩阵的特征值和特征向量
设 A 是一个 n×n 的方阵。如果存在一个非零列向量 v 和一个标量 λ,使得:![]()
那么 λ 称为矩阵 A的特征值,v 称为对应于特征值 λ 的特征向量。
注:λ可以为0,而v不能为0,并且v是列向量。因为A是n维矩阵,如果v是行向量,则维数是1xn,不满足矩阵相乘。
将定义中的等式移项,得到:![]()
由于v是非零列向量,相当于求上述方程的非零解,由方程有非零解的充要条件是行列式为0的定理可知:
![]()
说明:(A-λE):特征矩阵;|A-λE|:特征行列式或特征多项式;|A-λE|=0:特征方程
结论:
1.λ是A的特征值,v是对应λ的一个特征向量,则cv也是λ的一个特征向量,c为不等于0的标量。
根据定义:
![]()
等式两边同乘以c
![]()
所以cv也是λ的一个特征向量。
1.4向量的模
1.4.1向量的模的定义
向量 v 的模记作 ∥v∥,计算公式为:

1.4.2向量的模的几何解释
在二维空间中,向量 v=(v1,v2)的模表示从原点到点 (v1,v2)的距离。在三维空间中,向量 v=(v1,v2,v3)的模表示从原点到点 (v1,v2,v3)的距离。
||v||=1,叫做单位向量的模。如:v=(1,0,0)
1.4.3向量的模的性质
- 非负性
∥v∥≥0,并且 ∥v∥=0 当且仅当 v=0(零向量)。
- 齐次性
对于任意标量 k,∥kv∥=∣k∣∥v∥。
- 三角不等式
对于任意向量 u 和 v,∥u+v∥≤∥u∥+∥v∥。

1.5向量的内积
1.5.1向量的内积的定义
对于两个 n 维向量 a=(a1,a2,…,an) 和 b=(b1,b2,…,bn),它们的内积(点积)表示为 a⋅b,计算公式为:
![]()
1.5.2向量的内积的几何解释
在几何上,内积也可以通过向量的模和它们之间的夹角来表示。具体来说,如果 θ 是向量 a 和 b 之间的夹角,那么内积可以表示为:
![]()
其中:
-
∥a∥ 和 ∥b∥ 分别是向量 a 和 b 的模(长度)。
-
cos(θ)是夹角 θ 的余弦值。
结论:
向量内积的几何解释其实就是余弦相似度算法的公式,当cos(θ)=1时,表示两个向量重合;当cos(θ)=0时,表示两个向量垂直。
如果使用两个向量分别近似表示两个文本或图像
- 两个向量的cos(θ)越接近1,表示这两个文本内容越相似
- cos(θ)越接近0,表示这两个文本内容越不相似。
1.5.3向量的内积的性质
- 交换律:a⋅b=b⋅a
- 分配律:a⋅(b+c)=a⋅b+a⋅c
- 数乘结合律:(ka)⋅b=k(a⋅b)=a⋅(kb)
- 正定性:a⋅a≥0,并且 a⋅a=0 当且仅当 a=0。
相关文章:

线性代数基础02
目录 1.向量 1.1向量的定义 1.2向量的运算 1.2.1向量加法 1.2.2向量数乘 1.2.3向量点积 1.3矩阵的特征值和特征向量 1.4向量的模 1.4.1向量的模的定义 1.4.2向量的模的几何解释 1.4.3向量的模的性质 1.5向量的内积 1.5.1向量的内积的定义 1.5.2向量的内积的几何解…...

「4.4」祖孙询问
「4.4」祖孙询问 题目描述 已知一棵 n 个节点的有根树。有 m 个询问,每个询问给出了一对节点的编号 x 和 y,询问 x 与 y 的祖孙关系。 输入格式 输入第一行包括一个整数 n 表示节点个数; 接下来 n 行每行一对整数对 a 和 b 表示 a 和 b 之…...

Datawhale 组队学习 文生图 Prompt攻防 task03随笔
这期我们从不同角度切入探讨赛题的进阶思路 思路1:对比不同大模型 首先我们可以选择尝试不同的大模型,使用更复杂的大模型可以提高文本改写的质量和效果。随着模型大小的增加,其表示能力也随之增强,能够捕捉更细微的语言特征和语…...

游戏投屏软件有哪些?分享这10款比较好用的!
说到投屏,这个事情我还是比较有发言权的! 一般手机下载个APP,然后就可以通过WiFi、蓝牙或者USB进行连接投屏啦,下面是国内比较主流的一些游戏投屏软件,可以根据他们的优缺点进行选择哦! 01.幕连 国内首款…...

[Unity Demo]从零开始制作空洞骑士Hollow Knight第十六集(下篇):制作小BOSS龙牙哥
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、制作小BOSS龙牙哥 1.导入素材制作动画2.制作两种攻击行为3.制作从惊醒到转身到走路or跑步行为总结 前言 hello大家好久没见,之所以隔了一天时间…...

顺序表算法题【不一样的解法!】
本章概述 算法题1算法题2算法题3彩蛋时刻!!! 算法题1 力扣:移除元素 我们先来看这个题目的要求描述: 把与val相同数值的元素移除掉,忽略元素的相对位置变化,然后返回剩下与val值不同的元素个数…...

VuePress的基本常识
今天大概了解了一下Vuepress,感觉很棒,看着极其简单,自己也想做一个,后续我大概率也会做一个用Vuepress为基础做的博客网站,很酷~ 哈哈哈,下面是我今天学习Vuepress的一些内容,简单分享下&#…...

深入解析Vue2与Vue3的区别与Vue3的提升
Vue.js作为一款流行的前端框架,自发布以来,凭借其简洁的语法、灵活的组件化和高效的性能,赢得了众多开发者的喜爱。随着Vue3的发布,许多新特性和新功能也应运而生。那么,Vue2与Vue3究竟有哪些区别呢?Vue3又…...

认识python数据分析
Python作为一种高效、灵活且易于学习的编程语言,在数据分析领域展现出了强大的应用潜力。 从数据清洗、预处理到复杂的统计分析、可视化及机器学习模型的构建,Python提供了丰富的库和框架,极大地简化了数据分析的流程,提高了工作…...

以太网交换安全:MAC地址漂移与检测(实验:二层环路+网络攻击)
一、什么是MAC地址漂移? MAC地址漂移是指网络中设备的MAC地址在运行过程中发生变化的现象。 MAC地址是用于唯一标识网络中的设备。 MAC地址漂移是指交换机上一个VLAN内有两个端口学习到同一个MAC地址,后学习到的MAC地址表项覆盖原MAC地址表项的现象。…...

NeRF三维重建—神经辐射场Neural Radiance Field(二)体渲染相关
NeRF三维重建—神经辐射场Neural Radiance Field(二)体渲染相关 粒子采集部分 粒子采集的部分我们可以理解为,在已知粒子的情况下,对图片进行渲染的一个正向的过程。 空间坐标(x,y,z)发射的光线通过相机模型成为图片上…...

软件测试工程师:如何写出好的测试用例?
软件测试用例(Test Case)是软件测试过程中的一种详细文档或描述,用于描述在特定条件下,对软件系统或组件进行测试的步骤、输入数据、预期输出和预期行为。编写高质量的测试用例是确保软件质量的关键步骤之一。以下是一些编写优秀测试用例的建议ÿ…...

「图::连通」详解并查集并实现对应的功能 / 手撕数据结构(C++)
目录 概述 成员变量 创建销毁 根节点访问 路径压缩 启发式合并 复杂度 Code 概述 并查集,故名思议,能合并、能查询的集合,在图的连通性问题和许多算法优化上着广泛的使用。 这是一个什么数据结构呢? 一般来讲,并查集是…...

基于PSO粒子群优化的CNN-GRU-SAM网络时间序列回归预测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 (完整程序运行后无水印) PSO优化过程: PSO优化前后,模型训练对比: 数据预测对比: 误差回归对比&a…...

PyTorch 的 DataLoader 类介绍
DataLoader 类 功能与作用 PyTorch 是一个流行的开源机器学习库,它提供了一个名为 DataLoader 的类,用于加载数据集并将其封装成一个可迭代的对象。DataLoader 可以自动地将数据集划分为多个批次,并在训练过程中迭代地返回这些批次。是用于加…...

【设计模式系列】命令模式
目录 一、什么是命令模式 二、命令模式的角色 三、命令模式的典型应用场景 四、命令模式在Runnable中的应用 一、什么是命令模式 命令模式(Command Pattern)是一种行为设计模式,它将一个请求或简单操作封装为一个对象。这个模式提供了一种…...

uniapp中使用lottie实现JSON动画
uniapp中使用lottie实现JSON动画 不喜欢废话直接开干一、引入相关依赖二、在项目的目录新建目录结构三、操作步骤四、编写自定义组件代码五、组件的使用提一嘴更多lottie-web常用方法添加点击事件 不喜欢废话直接开干 一、引入相关依赖 npm install lottie-web # 如果有问题可…...
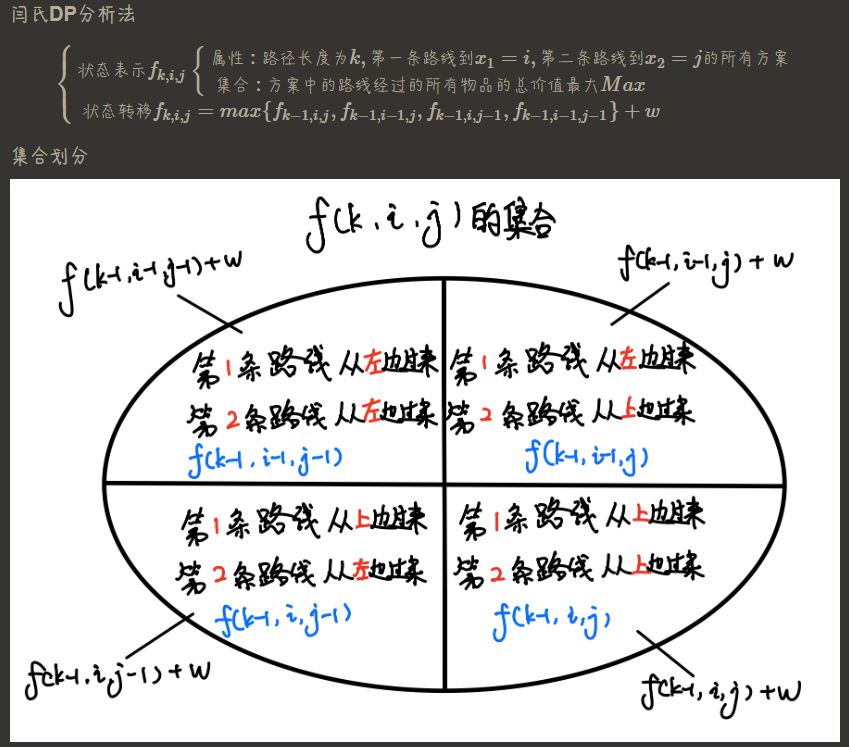
AcWing275
题目重述 这道题的核心是利用方格取数模型的思想,将两条路径的传递过程映射为同时出发的两条路径,避免重复格子的经过。题解通过以下步骤解题: 路径映射:从 (n, m) 回到 (1, 1) 的路径,可以转换成 (1, 1) 到 (n, m) …...

Windows系统部署redis自启动服务【亲测可用】
文章目录 引言I redis以本地服务运行(Windows service)使用MSI安装包配置文件,配置端口和密码II redis服务以终端命令启动缺点运行redis-server并指定端口和密码III 知识扩展确认redis-server可用性Installing the Service引言 服务器是Windows系统,所以使用Windows不是re…...

深入了解机器学习 (Descending into ML):线性回归
人们早就知晓,相比凉爽的天气,蟋蟀在较为炎热的天气里鸣叫更为频繁。数十年来,专业和业余昆虫学者已将每分钟的鸣叫声和温度方面的数据编入目录。Ruth 阿姨将她喜爱的蟋蟀数据库作为生日礼物送给您,并邀请您自己利用该数据库训练一…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

