NeRF三维重建—神经辐射场Neural Radiance Field(二)体渲染相关
NeRF三维重建—神经辐射场Neural Radiance Field(二)体渲染相关
粒子采集部分
粒子采集的部分我们可以理解为,在已知粒子的情况下,对图片进行渲染的一个正向的过程。
- 空间坐标(x,y,z)
- 发射的光线通过相机模型成为图片上的像素坐标(u,v)
- 粒子颜色即为像素颜色
- (u, v)与(x, y, z)的公式如下:也就是之前在相机模型中提到的一些有关坐标转化的部分知识。

内参+外参来进行的
相反我们的任务是给定一张图片,我们需要的是在许多张图片中推导出相机为位姿信息。
- 可以看作是沿着某一条射线上的无数个发光点的“和”;
- 利用相机模型,反推射线
- 那么这个射线表示为:r(t)=o+td
- O为射线原点,d为方向,t为距离
- 极坐标表示
总结来说我们的这个过程就是相机模型的一个反向的过程表达。由像素(u,v)反推出像素的信息来。

在三维的空间中采样射线的信息。
这一部分就是我们有关的粒子采集的部分信息了。可以得到我们的原点和方向的信息。我们通过这两个信息就可以表示出这条射线了。
体渲染
我们最后得到的像素的颜色是无数个发光粒子在该射线长度上经过累计得到的和。(作为我们像素最终的颜色)。
我们在表示出的这条射线上采用一定的方法取发光粒子的值,最后通过积分就可以得出体渲染所得到的像素的位置坐标了。
r ( t ) = o + t d r(t)=o+td r(t)=o+td
在我们计算的时候这个t是离散化的,我们如何通过选择这个离散的t来进行计算呢?
- 方法1:设置near=2,far=6。在near和far之间均匀采样64个点
- 通过图像和相机的位姿,来计算表示一条射线。
- 在射线上均匀的采样了64个点
- 训练时,一张图片取1024个像素,
- 得到1024条射线,每条射线上采样64个粒子共1024*64个粒子
我们的输出就是粒子的密度和颜色值
对之前的模型的信息进行一定的补充:
γ ( p ) = ( sin ( 2 0 π p ) , cos ( 2 0 π p ) , … , sin ( 2 L − 1 ) , cos ( 2 L − 1 π p ) ) \gamma(p)=\left(\sin \left(2^{0} \pi p\right), \cos \left(2^{0} \pi p\right), \ldots, \sin \left(2^{L-1}\right), \cos \left(2^{L-1} \pi p\right)\right) γ(p)=(sin(20πp),cos(20πp),…,sin(2L−1),cos(2L−1πp))
- p需要归一化到[-1,1]
- 对于空间坐标x,L=10,r(x)是60D
- 对于视角坐标d,L= 4,r(d)是24D
- 在代码中,加上初始值:r(x)是63D,r(d)是27D
LOSS
- GT是图片某一像素的RGB
- 将该像素对应光线上的粒子颜色进行求和
- 粒子的颜色和:该像素颜色的预测值
- 粒子的颜色和]与像素颜色做MSE(均方误差损失)
L = ∑ r ∈ R ∥ C ^ ( r ) − C ( r ) ∥ 2 2 R 是每个batch的射线(1024条) \begin{array}{l} L=\sum_{r \in R}\|\hat{C}(r)-C(r)\|_{2}^{2}\\ R \text { 是每个batch的射线(1024条) } \end{array} L=∑r∈R∥C^(r)−C(r)∥22R 是每个batch的射线(1024条)
体渲染连续积分
C ( s ) ^ = ∫ 0 + ∞ T ( s ) σ ( s ) C ( s ) d s T ( s ) = e − ∫ 0 s σ ( t ) d t \begin{array}{l} \hat{C(s)}=\int_{0}^{+\infty} T(s) \sigma(s) C(s) d s \\ T(s)=e^{-\int_{0}^{s} \sigma(t) d t} \end{array} C(s)^=∫0+∞T(s)σ(s)C(s)dsT(s)=e−∫0sσ(t)dt
- T(s):在s点之前,光线没有被阻碍的概率.
- o(s):在s点处,光线碰击粒子(光线被粒子阻碍)的概率密度
- C(s):在s点处,粒子光出的颜色
- 各点的颜色和概率密度已知,要先求T(s)
每个点的体密度与颜色相乘在结合一下不透明度来进行说明。
理论推导部分说明:

- 我们对上面的公式进行推导首先推导T的公式
T ( s + d s ) = T ( s ) [ 1 − σ ( s ) d s ] T ( s + d s ) = T ( s ) − T ( s ) σ ( s ) d s T ( s + d s ) − T ( s ) = − T ( s ) σ ( s ) d s d T ( s ) = − T ( s ) σ ( s ) d s d T ( s ) T ( s ) = − σ ( s ) d s \begin{array}{l} T(s+d s)=T(s)[1-\sigma(s) d s] \\ T(s+d s)=T(s)-T(s) \sigma(s) d s \\ T(s+d s)-T(s)=-T(s) \sigma(s) d s \\ d T(s)=-T(s) \sigma(s) d s \\ \frac{d T(s)}{T(s)}=-\sigma(s) d s \end{array} T(s+ds)=T(s)[1−σ(s)ds]T(s+ds)=T(s)−T(s)σ(s)dsT(s+ds)−T(s)=−T(s)σ(s)dsdT(s)=−T(s)σ(s)dsT(s)dT(s)=−σ(s)ds
两边同时积分就可以得到:
∫ 0 t d T ( s ) T ( s ) = ∫ 0 t − σ ( s ) d s ∫ 0 t 1 T ( s ) d T ( s ) = ∫ 0 t − σ ( s ) d s ln T ( s ) ∣ 0 t = ∫ 0 t − σ ( s ) d s ln T ( t ) − ln T ( 0 ) = ∫ 0 t − σ ( s ) d s ln T ( t ) = ∫ 0 t − σ ( s ) d s T ( t ) = e ∫ 0 t − σ ( s ) d s \begin{aligned} \int_{0}^{t} \frac{d T(s)}{T(s)} & =\int_{0}^{t}-\sigma(s) d s \\ \int_{0}^{t} \frac{1}{T(s)} d T(s) & =\int_{0}^{t}-\sigma(s) d s \\ \left.\ln T(s)\right|_{0} ^{t} & =\int_{0}^{t}-\sigma(s) d s \\ \ln T(t)-\ln T(0) & =\int_{0}^{t}-\sigma(s) d s \\ \ln T(t) & =\int_{0}^{t}-\sigma(s) d s \\ T(t) & =e^{\int_{0}^{t}-\sigma(s) d s} \end{aligned} ∫0tT(s)dT(s)∫0tT(s)1dT(s)lnT(s)∣0tlnT(t)−lnT(0)lnT(t)T(t)=∫0t−σ(s)ds=∫0t−σ(s)ds=∫0t−σ(s)ds=∫0t−σ(s)ds=∫0t−σ(s)ds=e∫0t−σ(s)ds
因为是离散的数据我们要将之前推导出来的连续形式进行离散化的处理。
- 计算机只能处理离散化数据
- 将光线[O,s]划分为N个等间距区间[Tn→ Tn+1]
- n=0,1,2,…,N
- 间隔长度为on
C ^ ( r ) = ∑ i = 1 N T i ( 1 − e − σ i δ i ) c i where T i = e − ∑ j = 1 i − 1 σ j δ j \begin{array}{l} \hat{C}(r)=\sum_{i=1}^{N} T_{i}\left(1-e^{-\sigma_{i} \delta_{i}}\right) c_{i}\\ \text { where } T_{i}=e^{-\sum_{j=1}^{i-1} \sigma_{j} \delta_{j}} \end{array} C^(r)=∑i=1NTi(1−e−σiδi)ci where Ti=e−∑j=1i−1σjδj
下面我们补充我们的离散化公式的一个推导过程。
我们对每个光区贡献的光强进行累计操作。
C ^ = ∑ n = 0 N I ( T n → T n + 1 ) \hat{C}=\sum_{n=0}^{N} I\left(T_{n} \rightarrow T_{n+1}\right) C^=n=0∑NI(Tn→Tn+1)
I ( T n → T n + 1 ) = ∫ t n t n + 1 T ( t ) σ n C n d t = σ n C n ∫ t n t n + 1 T ( t ) d t = σ n C n ∫ t n t n + 1 e − ∫ 0 t σ ( s ) d s d t = σ n C n ∫ t n t n + 1 e − ( ∫ 0 t n σ ( s ) d s + ∫ t n t σ ( s ) d s ) d t = σ n C n ∫ t n t n + 1 e − ∫ 0 t n σ ( s ) d s e − ∫ t n t σ ( s ) d s d t = σ n C n T ( 0 → t n ) ∫ t n t n + 1 e − ∫ t n t σ ( s ) d s d t \begin{aligned} I\left(T_{n} \rightarrow T_{n+1}\right) & =\int_{t_{n}}^{t_{n+1}} T(t) \sigma_{n} C_{n} d t \\ & =\sigma_{n} C_{n} \int_{t_{n}}^{t_{n+1}} T(t) d t \\ & =\sigma_{n} C_{n} \int_{t_{n}}^{t_{n+1}} e^{-\int_{0}^{t} \sigma(s) d s} d t \\ & =\sigma_{n} C_{n} \int_{t_{n}}^{t_{n+1}} e^{-\left(\int_{0}^{t_{n}} \sigma(s) d s+\int_{t_{n}}^{t} \sigma(s) d s\right)} d t \\ & =\sigma_{n} C_{n} \int_{t_{n}}^{t_{n+1}} e^{-\int_{0}^{t_{n}} \sigma(s) d s} e^{-\int_{t_{n}}^{t} \sigma(s) d s} d t \\ & =\sigma_{n} C_{n} T\left(0 \rightarrow t_{n}\right) \int_{t_{n}}^{t_{n+1}} e^{-\int_{t_{n}}^{t} \sigma(s) d s} d t \end{aligned} I(Tn→Tn+1)=∫tntn+1T(t)σnCndt=σnCn∫tntn+1T(t)dt=σnCn∫tntn+1e−∫0tσ(s)dsdt=σnCn∫tntn+1e−(∫0tnσ(s)ds+∫tntσ(s)ds)dt=σnCn∫tntn+1e−∫0tnσ(s)dse−∫tntσ(s)dsdt=σnCnT(0→tn)∫tntn+1e−∫tntσ(s)dsdt
经过化简就可以得到最后的公式的形式:
I ( T n → T n + 1 ) = σ n C n T ( 0 → t n ) ∫ t n t n + 1 e − ∫ t n t σ n d s d t = σ n C n T ( 0 → t n ) ∫ t n t n + 1 e − σ n ( t − t n ) d t = σ n C n T ( 0 → t n ) [ − 1 σ n e − σ n ( t − t n ) ∣ t n t n + 1 ] = C n T ( 0 → t n ) ( 1 − e σ n δ n ) = C n e − ∑ i = 0 n − 1 σ i δ i ( 1 − e σ n δ n ) . \begin{aligned} I\left(T_{n} \rightarrow T_{n+1}\right) & =\sigma_{n} C_{n} T\left(0 \rightarrow t_{n}\right) \int_{t_{n}}^{t_{n+1}} e^{-\int_{t_{n}}^{t} \sigma_{n} d s} d t \\ & =\sigma_{n} C_{n} T\left(0 \rightarrow t_{n}\right) \int_{t_{n}}^{t_{n+1}} e^{-\sigma_{n}\left(t-t_{n}\right)} d t \\ & =\sigma_{n} C_{n} T\left(0 \rightarrow t_{n}\right)\left[-\left.\frac{1}{\sigma_{n}} e^{-\sigma_{n}\left(t-t_{n}\right)}\right|_{t_{n}} ^{t_{n+1}}\right] \\ & =C_{n} T\left(0 \rightarrow t_{n}\right)\left(1-e^{\sigma_{n} \delta_{n}}\right) \\ & =C_{n} e^{-\sum_{i=0}^{n-1} \sigma_{i} \delta_{i}}\left(1-e^{\sigma_{n} \delta_{n}}\right). \end{aligned} I(Tn→Tn+1)=σnCnT(0→tn)∫tntn+1e−∫tntσndsdt=σnCnT(0→tn)∫tntn+1e−σn(t−tn)dt=σnCnT(0→tn)[−σn1e−σn(t−tn) tntn+1]=CnT(0→tn)(1−eσnδn)=Cne−∑i=0n−1σiδi(1−eσnδn).
- 粗模型:输入均匀采样粒子,输出密度
- 细模型:根据密度,二次采样
- 最后输出:采用模型2的输出
- 粗模型和细模型结构相同
相关文章:

NeRF三维重建—神经辐射场Neural Radiance Field(二)体渲染相关
NeRF三维重建—神经辐射场Neural Radiance Field(二)体渲染相关 粒子采集部分 粒子采集的部分我们可以理解为,在已知粒子的情况下,对图片进行渲染的一个正向的过程。 空间坐标(x,y,z)发射的光线通过相机模型成为图片上…...

软件测试工程师:如何写出好的测试用例?
软件测试用例(Test Case)是软件测试过程中的一种详细文档或描述,用于描述在特定条件下,对软件系统或组件进行测试的步骤、输入数据、预期输出和预期行为。编写高质量的测试用例是确保软件质量的关键步骤之一。以下是一些编写优秀测试用例的建议ÿ…...

「图::连通」详解并查集并实现对应的功能 / 手撕数据结构(C++)
目录 概述 成员变量 创建销毁 根节点访问 路径压缩 启发式合并 复杂度 Code 概述 并查集,故名思议,能合并、能查询的集合,在图的连通性问题和许多算法优化上着广泛的使用。 这是一个什么数据结构呢? 一般来讲,并查集是…...

基于PSO粒子群优化的CNN-GRU-SAM网络时间序列回归预测算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 (完整程序运行后无水印) PSO优化过程: PSO优化前后,模型训练对比: 数据预测对比: 误差回归对比&a…...

PyTorch 的 DataLoader 类介绍
DataLoader 类 功能与作用 PyTorch 是一个流行的开源机器学习库,它提供了一个名为 DataLoader 的类,用于加载数据集并将其封装成一个可迭代的对象。DataLoader 可以自动地将数据集划分为多个批次,并在训练过程中迭代地返回这些批次。是用于加…...

【设计模式系列】命令模式
目录 一、什么是命令模式 二、命令模式的角色 三、命令模式的典型应用场景 四、命令模式在Runnable中的应用 一、什么是命令模式 命令模式(Command Pattern)是一种行为设计模式,它将一个请求或简单操作封装为一个对象。这个模式提供了一种…...

uniapp中使用lottie实现JSON动画
uniapp中使用lottie实现JSON动画 不喜欢废话直接开干一、引入相关依赖二、在项目的目录新建目录结构三、操作步骤四、编写自定义组件代码五、组件的使用提一嘴更多lottie-web常用方法添加点击事件 不喜欢废话直接开干 一、引入相关依赖 npm install lottie-web # 如果有问题可…...
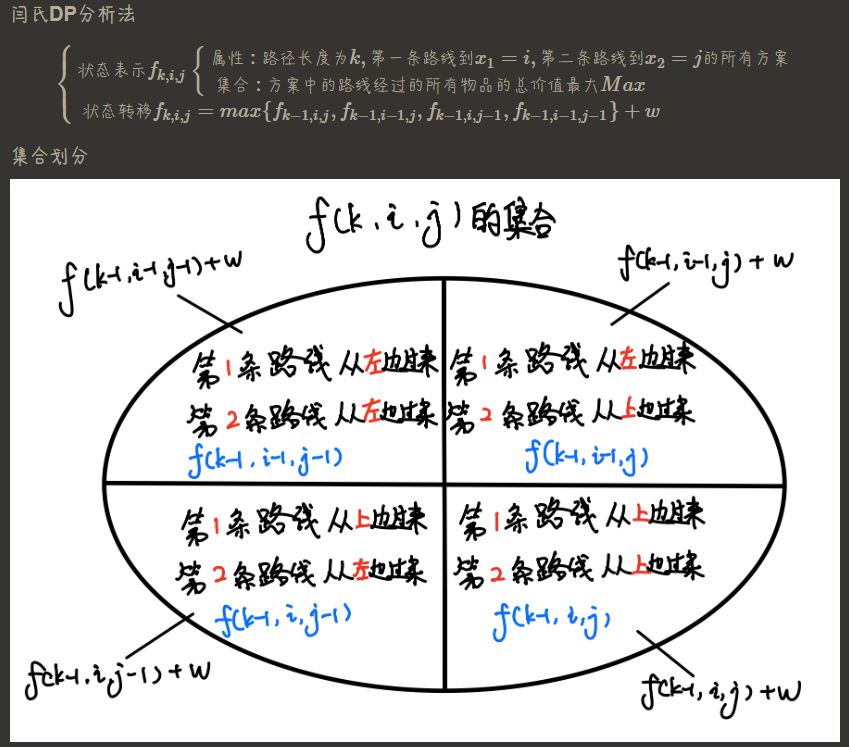
AcWing275
题目重述 这道题的核心是利用方格取数模型的思想,将两条路径的传递过程映射为同时出发的两条路径,避免重复格子的经过。题解通过以下步骤解题: 路径映射:从 (n, m) 回到 (1, 1) 的路径,可以转换成 (1, 1) 到 (n, m) …...

Windows系统部署redis自启动服务【亲测可用】
文章目录 引言I redis以本地服务运行(Windows service)使用MSI安装包配置文件,配置端口和密码II redis服务以终端命令启动缺点运行redis-server并指定端口和密码III 知识扩展确认redis-server可用性Installing the Service引言 服务器是Windows系统,所以使用Windows不是re…...

深入了解机器学习 (Descending into ML):线性回归
人们早就知晓,相比凉爽的天气,蟋蟀在较为炎热的天气里鸣叫更为频繁。数十年来,专业和业余昆虫学者已将每分钟的鸣叫声和温度方面的数据编入目录。Ruth 阿姨将她喜爱的蟋蟀数据库作为生日礼物送给您,并邀请您自己利用该数据库训练一…...

每日OJ题_牛客_集合_排序_C++_Java
目录 牛客_集合_排序 题目解析 C代码 Java代码 牛客_集合_排序 集合_牛客题霸_牛客网 (nowcoder.com) 题目解析 笔试题可直接用set排序,面试可询问是否要手写排序函数,如果要手写排序,推荐写快排。 C代码 #include <iostream> …...
鸿蒙网络编程系列27-HTTPS服务端证书的四种校验方式示例
1. 服务端数字证书验证的问题 在鸿蒙客户端对服务端发起HTTPS请求时,如果使用HttpRequest的request发起请求,那么就存在服务端数字证书的验证问题,你只有两个选择,一个是使用系统的CA,一个是使用自己选定的CA…...

scala继承
Scala中继承的定义为在原有类的基础上定义一个新类,原有类称为父类,新类称为子类。 当子类从父类中继承的方法不能满足需要时,子类需要有自己的行为,怎么办? 此时使用override可以重写父类方法。 class Aniaml(){va…...

【Hive】2-Apache Hive概述、架构、组件、数据模型
Apache Hive概述 什么是Hive Apache Hive是一款建立在Hladoop之上的开源数据仓库系统,可以将存储在Hadoop文件中的结构化、半结构化数据文件映射为一张数据库表,基于表提供了一种类似SQL的查询模型,称为Hive查询语言(HQL),用于访…...

关于目前面试八股文的一些心得体会
现在是2024年10月,自22年开始,明显感觉到整个计算机行业,越来越卷了。一方面,随着信息的传播,越来越多的新人涌入了这个赛道,另一方面,众所周知的原因,不管大厂还是小厂在经历寒冬之…...

大数据-178 Elasticsearch Query - Java API 索引操作 文档操作
点一下关注吧!!!非常感谢!!持续更新!!! 目前已经更新到了: Hadoop(已更完)HDFS(已更完)MapReduce(已更完&am…...

PHP(一)从入门到放弃
参考文献:https://www.php.net/manual/zh/introduction.php PHP 是什么? PHP(“PHP: Hypertext Preprocessor”,超文本预处理器的字母缩写)是一种被广泛应用的开放源代码的多用途脚本语言,它可嵌入到 HTML…...

基于深度学习的生物启发的学习系统
基于深度学习的生物启发学习系统(Biologically Inspired Learning Systems)旨在借鉴生物大脑的结构和学习机制,设计出更高效、更灵活的人工智能系统。这类系统融合了生物神经科学的研究成果,通过模仿大脑中的学习模式、记忆过程和…...

10_实现readonly
在某些时候,我们希望定义一些数据是只读的,不允许被修改,从而实现对数据的保护,即为 readonly 只读本质上也是对数据对象的代理,我们同样可以基于之前实现的 createReactiveObject 函数来实现,可以为此函数…...

简单介绍$listeners
$listeners 它可以获取父组件传递过来的所有自定义函数,如下: // 父组件 <template><div class"a"><Child abab"handleAbab" acac"handleAcac"/></div> </template><script> impor…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
