G - Road Blocked 2
G - Road Blocked 2
思路
只有当一条边是从 1 1 1到 n n n的所有最短路构成的图的桥时,去掉这条边,最短路才会变大
所以就可以用最短路加tarjan解决这道题了
怎么判断一条边是否可以构成最短路呢,比如求 1 1 1到 n n n的最短路,分别求出dist1(源点为1)和distn(源点为n),当一条边(端点分别为a,b,边长为w)包含再最短路之中时,它满足如下条件
dist1[n]=dist1[a]+w+distn[b]||dist1[n]=distn[a]+w+dist1[b]
当然还有其它方法,我写的代码就是其他方法,只是上面的方法更简单罢了
代码
struct Edge{int a,b,c;
};void solve() {int n,m;cin>>n>>m;vector<vector<pii>> g(n+1);vector<Edge> es(m+1);for(int i=1;i<=m;i++){int a,b,c;cin>>a>>b>>c;es[i]={a,b,c};g[a].push_back({b,i}),g[b].push_back({a,i});}vector<bool> st(n+1);vector<ll> dist(n+1,1ll<<60);priority_queue<pll,vector<pll>,greater<pll>> q;dist[1]=0;q.push({dist[1],1});vector<vector<pii>> pas(n+1);while(q.size()){auto [dis,ver]=q.top();q.pop();if(st[ver]) continue;st[ver]=true;for(auto [y,id]:g[ver]){int w=es[id].c;if(dist[y]>dis+w){pas[y].clear();pas[y].push_back({ver,id});dist[y]=dis+w;q.push({dist[y],y}); }else if(dist[y]==dis+w){pas[y].push_back({ver,id});}}}vector<bool> st1(n+1);vector<vector<pii>> fg(n+1);auto dfs=[&](auto && self,int u)->void{if(st1[u]) return;st1[u]=true;for(auto [ver,id]:pas[u]){fg[u].push_back({ver,id}),fg[ver].push_back({u,id});self(self,ver);}};dfs(dfs,n);vector<int> dfn(n+1),low(n+1);vector<bool> fst(m+1);int timestamp=0;auto tarjan=[&](auto && self,int u,int fa)->void{dfn[u]=low[u]=++timestamp;for(auto [y,id]:fg[u]){if(!dfn[y]){self(self,y,u);low[u]=min(low[u],low[y]);if(low[y]>dfn[u]){fst[id]=true;}}else if(y!=fa){low[u]=min(low[u],dfn[y]);}}};tarjan(tarjan,1,0);for(int i=1;i<=m;i++){cout<<(fst[i]?"Yes":"No")<<endl;}
}
相关文章:

G - Road Blocked 2
G - Road Blocked 2 思路 只有当一条边是从 1 1 1到 n n n的所有最短路构成的图的桥时,去掉这条边,最短路才会变大 所以就可以用最短路加tarjan解决这道题了 怎么判断一条边是否可以构成最短路呢,比如求 1 1 1到 n n n的最短路࿰…...

R语言绘制Venn图(文氏图、温氏图、维恩图、范氏图、韦恩图)
Venn图,又称文氏图,标题中其他名字也是它的别称,由封闭圆形组成,代表不同集合。圆形重叠部分表示集合交集,非重叠处为独有元素。在生物学、统计学等领域广泛应用,可展示不同数据集相似性与差异,…...

【Vue.js】vue2 项目在 Vscode 中使用 Ctrl + 鼠标左键跳转 @ 别名导入的 js 文件和 .vue 文件
js 文件跳转 需要安装插件 Vetur 然后需要我们在项目根目录下添加 jsconfig.json 配置,至于配置的作用,可以参考我的另外一篇博客: 【React 】react 创建项目配置 jsconfig.json 的作用 它主要用于配置 JavaScript 或 TypeScript 项目的根…...

NVM配置与Vue3+Vite项目快速搭建指南
本文目录 1、配置环境1.1 NVM1、nvm常用命令 1.2 Mac配置环境1、安装nvm 1.3 Window配置环境1、安装nvm 2、 项目搭建2.1 项目依赖2.2 安装依赖2.3 配置1、别名配置2、创建样式及图片文件夹3、路由 2.4 项目搭建效果2.5 项目结构 在当今快速发展的前端技术领域中,掌…...

面试“利器“——微学时光
大家好,我是程序员阿药。微学时光是一款专为计算机专业学生和IT行业求职者设计的面试刷题小程序,它汇集了丰富的计算机面试题和知识点,旨在帮助用户随时随地学习和复习,提高自身的技术能力和面试技巧。 主题 随时随地学习&#x…...

【Unity】【游戏开发】游戏引擎是如何模拟世界的
【核心感悟】 游戏引擎通过两个维度的合并来模拟这个时间。 一个维度叫物理模型。 一个维度叫视觉模型。 对于物理模型,我们需要用物理引擎给予行为。 对于视觉模型,我们需要用动画去给予行为。 物理模型是真实机制,视觉模型是艺术表现&…...

vscode配置conda虚拟环境【windows系统】
安装好anacondavscode里安装python插件 3.点击左侧插件 如图1,再2,再点击3小星星激活conda环境 最后下方栏就出现conda环境了。就可以用啦...

libgpiod在imx8平台交叉编译说明
如下记录是在 imx8上测试使用 参考博主的文章 iMX6ULL 库移植 | Libgpiod 库的交叉编译及使用指南(linux) 编译说明 1: build.sh代码如下所示,先执行 source build.sh,注意修改交叉编译工具链为自己本地的地址; 2:执行 ./autogen…...

无人机之自主飞行关键技术篇
无人机自主飞行指的是无人机利用先进的算法和传感器,实现自我导航、路径规划、环境感知和自动避障等能力。这种飞行模式大大提升了无人机的智能化水平和操作的自动化程度。 一、传感器技术 传感器是无人机实现自主飞行和数据采集的关键组件,主要包括&a…...

performance.timing
performance.timing 是 Web 性能 API 的一部分,用于获取页面加载过程中的各个时间戳。这些时间戳可以帮助开发者分析页面加载性能,找出潜在的瓶颈。performance.timing 返回一个 PerformanceTiming 对象,该对象包含了多个属性,每个…...
教你不用下载 maven,不用配置环境变量,在 idea 上创建 maven 项目
我的主页:2的n次方_ 1. Maven Maven是⼀个项⽬管理⼯具, 通过 pom.xml ⽂件的配置获取 jar 包,⽽不⽤⼿动去添加 jar 包,这样就大大的提高了开发效率 2. Maven 的核心功能 2.1. 项目构建 创建第一个 Maven 项目 Maven 提供了标准的…...

linux 设置tomcat开机启动
在Linux系统中,要配置Tomcat开机自启动,可以创建一个名为 tomcat.service 的 systemd 服务文件,并将其放置在 /etc/systemd/system/ 目录下。以下是一个基本的服务文件示例,假设Tomcat安装在 /usr/local/tomcat 路径下:…...

opencv出错以及解决技巧
opencv配置 一开始,include的路径是<opencv4/opencv2/…> 这样在using namespace cv的时候导致了报错, 所以在cmakelist中需要对cmake的版本进行升级。 set(CMAKE_CXX_FLAGS “-stdc14 -O0 -Wall”)-O0 表示在编译过程中不进行任何优化 对应的pac…...

Python爬虫进阶(实战篇一)
接,基础篇,链接:python爬虫入门(所有演示代码,均有逐行分析!)-CSDN博客 目录 1.爬取博客网站全部文章列表 ps:补充(正则表达式) 爬虫实现 爬虫代码: 2.爬…...
)
运维面试题(2)
ssh服务(重点)协议使用 端口 号:默认是 22, 可以是被修改的,如果需要修改,则需要修改 ssh 服务的配置文件:#/etc/ssh/ssh_config,可以通过这个配置文件来修改端口 端口号可以修改&am…...

Django CSRF Token缺失或不正确
在Django中,CSRF(跨站请求伪造)验证失败,提示“CSRF token missing or incorrect”的错误,通常是由以下几个原因造成的: 忘记在表单中添加 {% csrf_token %} 模板标签:这是最常见的原因之一。确…...
)
10.12Python数学基础-矩阵(下)
9.矩阵的转置 矩阵的转置(Transpose)是矩阵操作中的一种基本运算。它通过交换矩阵的行和列来生成一个新的矩阵。具体来说,如果 A 是一个 mn 的矩阵,那么它的转置矩阵 A^T 是一个 nm 的矩阵,其中 A^T 的第 i 行第 j 列…...

vue网络自学知识点汇总
初体验 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><!--1.引入vue.j…...
)
Springboot项目Activemq延迟自定义消息完整代码案例(亲测可用)
1、porm.xml增加依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-activemq</artifactId> </dependency> 2、application.properties增加配置 # 连接地址 spring.activemq.broker-url=fa…...
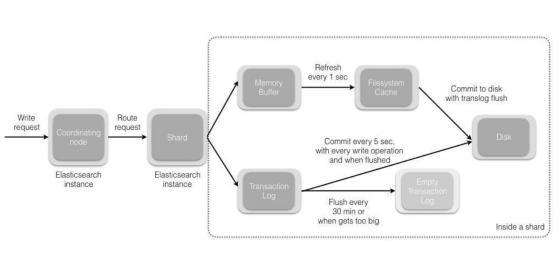
常见ElasticSearch 面试题解析(上)
前言 ElasticSearch是一个基于Lucene的搜索服务器。它提供了一个分布式多用户能力的全文搜索引擎,基于RESTful web接口。Elasticsearch是用Java语言开发的,并作为Apache许可条款下的开放源码发布,是一种流行的企业级搜索引擎。ElasticSearch…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
