10.12Python数学基础-矩阵(下)
9.矩阵的转置
矩阵的转置(Transpose)是矩阵操作中的一种基本运算。它通过交换矩阵的行和列来生成一个新的矩阵。具体来说,如果 A 是一个
m×n 的矩阵,那么它的转置矩阵 A^T 是一个 n×m 的矩阵,其中 A^T 的第 i 行第 j 列的元素等于 A 的第 j 行第i 列的元素。
定义
设 A 是一个 m×n 的矩阵,其元素为 aij,那么 A 的转置矩阵 A^T 是一个 n×m 的矩阵,其元素为 aji。
例子
假设有一个矩阵 A:
A = ( 1 2 3 4 5 6 ) A=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\end{pmatrix} A=(142536)
这个矩阵是一个 2×3 的矩阵。它的转置矩阵 A^T 是一个 3×2 的矩阵,计算如下:
A T = ( 1 4 2 5 3 6 ) A^{T}=\begin{pmatrix} 1 & 4 \\ 2 & 5\\3 & 6 \end{pmatrix} AT= 123456
性质
矩阵转置具有以下性质:
- (AT)T = A:一个矩阵的转置的转置等于原矩阵。
- (A + B)^T = A^T + B^T:两个矩阵和的转置等于它们各自转置的和。
- (kA)^T = kA^T:一个矩阵乘以一个标量的转置等于该矩阵的转置乘以该标量。
- (AB)^T = B^T A^T:两个矩阵乘积的转置等于它们各自转置的乘积,但顺序相反。
特殊矩阵
-
对称矩阵:如果一个矩阵 A 满足 A^T=A,那么 A 是对称矩阵。对称矩阵的元素关于主对角线对称。
如:
A = ( 1 1 3 1 1 4 3 4 1 ) A=\begin{pmatrix} 1 & 1 & 3 \\ 1 & 1 & 4 \\ 3 & 4 & 1\end{pmatrix} A= 113114341 -
反对称矩阵:如果一个矩阵 A 满足 A^T=−A,那么 A 是反对称矩阵。反对称矩阵的主对角线元素必须为零,且关于主对角线对称的元素互为相反数。
如:
A = ( 0 1 3 − 1 0 4 − 3 − 4 0 ) A=\begin{pmatrix} 0 & 1 & 3 \\ -1 & 0 & 4 \\ -3 & -4 & 0\end{pmatrix} A= 0−1−310−4340 A T = ( 0 − 1 − 3 1 0 − 4 3 4 0 ) = − A A^{T}=\begin{pmatrix} 0 & -1 & -3 \\ 1 & 0 & -4 \\ 3 & 4 & 0\end{pmatrix}=-A AT= 013−104−3−40 =−A
反对称矩阵:
a i j = − a j i a_{ij}=-a_{ji} aij=−aji
所以:
a i i = − a i i = > 2 a i i = 0 = > a i i = 0 a_{ii}=-a_{ii}=>2a_{ii}=0=>a_{ii}=0 aii=−aii=>2aii=0=>aii=0
得出主对角线元素必须为零。
对称矩阵和反对称矩阵都是方阵。
矩阵A和B为同阶对称矩阵,AB对称的充要条件为AB=BA
证明:
AB对称则
( A B ) T = A B (AB)^{T}=AB (AB)T=AB
同时
( A B ) T = B T A T (AB)^{T}=B^{T}A^{T} (AB)T=BTAT
由于A和B是对称矩阵,则
( A B ) T = B T A T = B A (AB)^{T}=B^{T}A^{T}=BA (AB)T=BTAT=BA
所以
A B = B A AB=BA AB=BA
思考:
A为反对称矩阵,则A^k为?
证明:
( A k ) T = ( A × A . . . × A ) T = A T × A T . . . × A T = ( − A ) × ( − A ) . . . × ( − A ) = ( − 1 ) k A k (A^{k})^{T}=(A\times A ...\times A)^{T}=A^{T}\times A^{T}...\times A^{T}=(-A)\times (-A)...\times (-A)=(-1)^{k}A^{k} (Ak)T=(A×A...×A)T=AT×AT...×AT=(−A)×(−A)...×(−A)=(−1)kAk
如果k为偶数,则
( A k ) T = A k (A^{k})^{T}=A^{k} (Ak)T=Ak
此时A^k为对称矩阵
如果k为奇数,则
( A k ) T = − A k (A^{k})^{T}=-A^{k} (Ak)T=−Ak
此时A^k为反对称矩阵
10.方阵的行列式
要计算行列式的前提为矩阵A为方阵。
性质:A为n阶的方阵
∣ A T ∣ = ∣ A ∣ |A^{T}|=|A| ∣AT∣=∣A∣
∣ k A ∣ = k n ∣ A ∣ |kA|=k^{n}|A| ∣kA∣=kn∣A∣
∣ − A ∣ = ( − 1 ) n ∣ A ∣ |-A|=(-1)^{n}|A| ∣−A∣=(−1)n∣A∣
∣ A B ∣ = ∣ A ∣ ∣ B ∣ |AB|=|A||B| ∣AB∣=∣A∣∣B∣
∣ A m ∣ = ∣ A ∣ m |A^{m}|=|A|^{m} ∣Am∣=∣A∣m
∣ E ∣ = 1 |E|=1 ∣E∣=1
例子
1.有矩阵A
A = ( 1 2 0 0 3 0 − 1 4 5 ) A=\begin{pmatrix} 1 & 2 & 0 \\ 0 & 3 & 0 \\ -1 & 4 & 5\end{pmatrix} A= 10−1234005
求|2A|和|A|A
解:
d e t ( A ) = ∣ 1 2 0 0 3 0 − 1 4 5 ∣ = 3 × ( − 1 ) 2 + 2 ∣ 1 0 − 1 5 ∣ = 15 det(A)=\begin{vmatrix} 1 & 2 & 0 \\ 0 & 3 & 0 \\ -1 & 4 & 5\end{vmatrix}=3\times (-1)^{2+2}\begin{vmatrix} 1 & 0\\-1 & 5 \end{vmatrix}=15 det(A)= 10−1234005 =3×(−1)2+2 1−105 =15
则
d e t ( 2 A ) = 2 3 d e t ( A ) = 120 det(2A)=2^{3}det(A)=120 det(2A)=23det(A)=120
d e t ( A ) A = 15 A = 15 ( 1 2 0 0 3 0 − 1 4 5 ) = ( 15 30 0 0 45 0 − 15 60 75 ) det(A)A=15A=15\begin{pmatrix} 1 & 2 & 0 \\ 0 & 3 & 0 \\ -1 & 4 & 5\end{pmatrix}=\begin{pmatrix} 15 & 30 & 0 \\ 0 & 45 & 0 \\ -15 & 60 & 75\end{pmatrix} det(A)A=15A=15 10−1234005 = 150−153045600075
2.A为n阶方阵,|A|=3,求
∣ ∣ A ∣ A T ∣ = ? ||A|A^{T}|=? ∣∣A∣AT∣=?
解:
∣ ∣ A ∣ A T ∣ = ∣ A ∣ n ∣ A T ∣ = ∣ A ∣ n + 1 = 3 n + 1 ||A|A^{T}|=|A|^{n}|A^{T}|=|A|^{n+1}=3^{n+1} ∣∣A∣AT∣=∣A∣n∣AT∣=∣A∣n+1=3n+1
11.伴随矩阵
设 A 是一个 n×n 的方阵,其元素为 aij。伴随矩阵 adj(A)或A* 是一个 n×n的矩阵,其第 i 行第 j 列的元素是 A 的余子式 Mji 的代数余子式 Cji,即:
( A ∗ ) i j = C j i = ( − 1 ) i + j M j i (A^{*})_{ij}=C^{ji}=(−1)^{i+j}M_{ji} (A∗)ij=Cji=(−1)i+jMji
其中 Mji是 A 的第j 行第i 列元素的余子式,即去掉第 j 行和第 i 列后剩下的 (n−1)×(n−1) 矩阵的行列式。
简单理解:
1.先按行求出每个元素的代数余子式
2.将每行元素的代数余子式按列组成一个矩阵,该矩阵就是伴随矩阵。
例如:
A = ( 1 1 1 2 1 3 1 1 4 ) A=\begin{pmatrix} 1 & 1 & 1 \\ 2 & 1 & 3 \\ 1 & 1 & 4\end{pmatrix} A= 121111134
求A的伴随矩阵A*
解:
按行求出每个元素的代数余子式:
C 11 = ( − 1 ) 1 + 1 ∣ 1 3 1 4 ∣ = 1 , C 12 = ( − 1 ) 1 + 2 ∣ 2 3 1 4 ∣ = − 5 , C 13 = ( − 1 ) 1 + 3 ∣ 2 1 1 1 ∣ = 1 C 21 = − 3 , C 22 = 3 , C 23 = 0 C 31 = 2 , C 32 = − 1 , C 33 = − 1 C_{11}=(-1)^{1+1}\begin{vmatrix} 1 & 3 \\ 1 & 4 \end{vmatrix}=1,C_{12}=(-1)^{1+2}\begin{vmatrix} 2 & 3 \\ 1 & 4 \end{vmatrix}=-5,C_{13}=(-1)^{1+3}\begin{vmatrix} 2 & 1 \\ 1 & 1 \end{vmatrix}=1\\ C_{21}=-3,C_{22}=3,C_{23}=0\\ C_{31}=2,C_{32}=-1,C_{33}=-1 C11=(−1)1+1 1134 =1,C12=(−1)1+2 2134 =−5,C13=(−1)1+3 2111 =1C21=−3,C22=3,C23=0C31=2,C32=−1,C33=−1
然后将每行元素的代数余子式按列组成矩阵:
C = ( 1 − 3 2 − 5 3 − 1 1 0 − 1 ) C=\begin{pmatrix} 1 & -3 & 2 \\ -5 & 3 & -1 \\ 1 & 0 & -1\end{pmatrix} C= 1−51−3302−1−1
性质:
A A ∗ = A ∗ A = ∣ A ∣ E AA^{*}=A^{*}A=|A|E AA∗=A∗A=∣A∣E
证明:
( a 11 C 11 + a 12 C 12 + . . . + a 1 n C 1 n 0 . . . 0 0 a 21 C 21 + a 22 C 22 + . . . + a 2 n C 2 n . . . 0 ⋮ 0 0 . . . a n 1 C n 1 + a n 2 C n 2 + . . . + a n n C n n ) = ( ∣ A ∣ 0 . . . 0 0 ∣ A ∣ . . . 0 ⋮ 0 0 . . . ∣ A ∣ ) = ∣ A ∣ E \begin{pmatrix} a_{11}C_{11}+a_{12}C_{12}+...+a_{1n}C_{1n} & 0 & ... & 0 \\ 0 & a_{21}C_{21}+a_{22}C_{22}+...+a_{2n}C_{2n} & ... & 0 \\& \vdots \\ 0 & 0 & ... & a_{n1}C_{n1}+a_{n2}C_{n2}+...+a_{nn}C_{nn}\end{pmatrix}\\=\begin{pmatrix}|A| & 0 & ... & 0 \\ 0 & |A| & ... & 0 \\& \vdots \\ 0 & 0 & ... & |A| \end{pmatrix}=|A|E a11C11+a12C12+...+a1nC1n000a21C21+a22C22+...+a2nC2n⋮0.........00an1Cn1+an2Cn2+...+annCnn = ∣A∣000∣A∣⋮0.........00∣A∣ =∣A∣E
性质2:
∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^{*}|=|A|^{n-1} ∣A∗∣=∣A∣n−1
证明:
∣ A A ∗ ∣ = ∣ A ∣ ∣ A ∗ ∣ = ∣ ∣ A ∣ E ∣ = ∣ A ∣ n ∣ E ∣ = ∣ A ∣ n |AA^{*}|=|A||A^{*}|=||A|E|=|A|^{n}|E|=|A|^{n} ∣AA∗∣=∣A∣∣A∗∣=∣∣A∣E∣=∣A∣n∣E∣=∣A∣n
所以
∣ A ∣ ∣ A ∗ ∣ = ∣ A ∣ n = > ∣ A ∣ ( ∣ A ∣ n − 1 − ∣ A ∗ ∣ ) = 0 |A||A^{*}|=|A|^{n}=>|A|(|A|^{n-1}-|A^{*}|)=0 ∣A∣∣A∗∣=∣A∣n=>∣A∣(∣A∣n−1−∣A∗∣)=0
得出
∣ A ∣ = 0 或 ∣ A ∗ ∣ = ∣ A ∣ n − 1 |A|=0 或 |A^{*}|=|A|^{n-1} ∣A∣=0或∣A∗∣=∣A∣n−1
如果|A|=0,则A中两行元素相等或成比例,或一行元素为0,则其代数余子式必有一行元素为0,所以
∣ A ∗ ∣ = 0 = 0 n − 1 = ∣ A ∣ n − 1 |A^{*}|=0=0^{n-1}=|A|^{n-1} ∣A∗∣=0=0n−1=∣A∣n−1
所以等式成立。
12.逆矩阵
对于一个 n×n 的方阵 A,如果存在另一个 n×n的方阵 B,使得 AB=BA=E,其中 E 是 n×n 的单位矩阵,那么 B 称为 A 的逆矩阵,记作
A − 1 A^{−1} A−1
逆矩阵的存在条件
一个矩阵 A 有逆矩阵的充分必要条件是 A 是可逆的,即 det(A)≠0。如果 det(A)=0,则 A 是奇异矩阵,没有逆矩阵。
思考:如果A可逆,则可逆矩阵是唯一的
证明:
假设可逆矩阵不是唯一的,存在两个可逆矩阵B1和B2,则由可逆矩阵定义可知:
A B 1 = B 1 A = E A B 2 = B 2 A = E AB_{1}=B_{1}A=E\\ AB_{2}=B_{2}A=E AB1=B1A=EAB2=B2A=E
则:
B 1 = B 1 E = B 1 ( A B 2 ) = ( B 1 A ) B 2 = E B 2 = B 2 B_{1}=B_{1}E=B_{1}(AB_{2})=(B_{1}A)B_{2}=EB_{2}=B_{2} B1=B1E=B1(AB2)=(B1A)B2=EB2=B2
所以可逆矩阵唯一。
性质:
1.n阶方阵A可逆的充要条件为
∣ A ∣ ≠ 0 |A|\neq 0 ∣A∣=0
且当A可逆时,
A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\dfrac{1}{|A|}A^{*} A−1=∣A∣1A∗
证明:
充分性:
因为
∣ A ∣ ≠ 0 |A|\neq 0 ∣A∣=0
则
A A ∗ = A ∗ A = ∣ A ∣ E = > A ( 1 ∣ A ∣ A ∗ ) = ( 1 ∣ A ∣ A ∗ ) A = E AA^{*}=A^{*}A=|A|E=>A(\dfrac{1}{|A|}A^{*})=(\dfrac{1}{|A|}A^{*})A=E AA∗=A∗A=∣A∣E=>A(∣A∣1A∗)=(∣A∣1A∗)A=E
所以A可逆,并且
A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\dfrac{1}{|A|}A^{*} A−1=∣A∣1A∗
必要性:
因为A可逆,则
A B = B A = E = > ∣ A B ∣ = ∣ A ∣ ∣ B ∣ = ∣ E ∣ = 1 AB=BA=E=>|AB|=|A||B|=|E|=1 AB=BA=E=>∣AB∣=∣A∣∣B∣=∣E∣=1
所以
∣ A ∣ ≠ 0 |A|\neq 0 ∣A∣=0
例子:
有矩阵A:
A = ( 1 0 1 2 1 0 − 3 2 − 5 ) A=\begin{pmatrix} 1 & 0 & 1 \\ 2 & 1 & 0 \\ -3 & 2 & -5\end{pmatrix} A= 12−301210−5
问矩阵A是否可逆,如果可逆,求可逆矩阵
解:
∣ A ∣ = ∣ 1 0 1 2 1 0 − 3 2 − 5 ∣ = − 5 + 4 + 3 = 2 ≠ 0 |A|=\begin{vmatrix} 1 & 0 & 1 \\ 2 & 1 & 0 \\ -3 & 2 & -5\end{vmatrix}=-5+4+3=2\neq 0 ∣A∣= 12−301210−5 =−5+4+3=2=0
所以A可逆
A − 1 = 1 ∣ A ∣ A ∗ = 1 2 ( − 5 2 − 1 10 − 2 2 7 − 2 1 ) A^{-1}=\dfrac{1}{|A|}A^{*}=\dfrac{1}{2}\begin{pmatrix} -5 & 2 & -1 \\ 10 & -2 & 2 \\ 7 & -2 & 1\end{pmatrix} A−1=∣A∣1A∗=21 −51072−2−2−121
2.设A、B 和 C 是 n×n 的可逆矩阵,那么它们的乘积 ABC的逆矩阵为:
( A B C ) − 1 = C − 1 B − 1 A − 1 (ABC)^{−1}=C^{−1}B^{−1}A^{−1} (ABC)−1=C−1B−1A−1
13.初等变换
初等变换一般可以分为两种类型:行变换、列变换。
初等行变换:
-
交换两行:将矩阵的第 i 行和第 j 行交换位置
如:矩阵第二行和第三行交换
( 1 2 3 4 5 6 7 8 9 ) − > ( 1 2 3 7 8 9 4 5 6 ) \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{pmatrix}->\begin{pmatrix} 1 & 2 & 3\\ 7 & 8 & 9 \\ 4 & 5 & 6 \end{pmatrix} 147258369 −> 174285396 -
某一行乘以非零常数:将矩阵的第i 行乘以一个非零常数 k
如:第二行乘以非零整数k
( 1 2 3 4 5 6 7 8 9 ) − > ( 1 2 3 4 k 5 k 6 k 7 8 9 ) \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{pmatrix}->\begin{pmatrix} 1 & 2 & 3 \\ 4k & 5k & 6k \\ 7 & 8 & 9\end{pmatrix} 147258369 −> 14k725k836k9 -
某一行加上另一行的倍数:将矩阵的第 i行加上第 j 行的 k 倍
如:矩阵第一行乘以-4加到第二行
( 1 2 3 4 5 6 7 8 9 ) − > ( 1 2 3 0 − 3 − 6 7 8 9 ) \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{pmatrix}->\begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -6 \\ 7 & 8 & 9\end{pmatrix} 147258369 −> 1072−383−69
初等列变换
- 交换两列:将矩阵的第 i 列和第 j 列交换位置
- 某一列乘以非零常数:将矩阵的第 i 列乘以一个非零常数 k
- 某一列加上另一列的倍数:将矩阵的第 i 列加上第 j 列的 k 倍
14.矩阵的标准形
常见的矩阵标准形包括行阶梯形矩阵、简化行阶梯形矩阵等。
14.1 行阶梯形矩阵
行阶梯形矩阵是一种特殊的矩阵形式,具有以下特征:
- 非零行在零行之上:所有非零行都在零行之上。
- 主元:每一行的第一个非零元素(主元)在上一行主元的右边。
- 主元下方元素为零:每一行的主元下方元素都为零。
例如,以下矩阵是一个行阶梯形矩阵:
( 1 2 3 0 5 6 0 0 9 ) , ( 1 2 3 4 0 5 6 7 0 0 0 9 ) \begin{pmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9\end{pmatrix},\begin{pmatrix} 1 & 2 & 3 & 4 \\ 0 & 5 & 6 & 7\\ 0 & 0 &0 & 9\end{pmatrix} 100250369 , 100250360479
简单理解为:用折线表示,竖线只过一个数,横线可过多个数
下边的矩阵不是行阶梯形矩阵
14.2 简化行阶梯形矩阵
简化行阶梯形矩阵是行阶梯形矩阵的一种特殊形式,具有以下特征:
- 非零行在零行之上:所有非零行都在零行之上。
- 主元为 1:每一行的第一个非零元素(主元)为 1。
- 主元下方元素为零:每一行的主元下方元素都为零。
- 主元上方元素为零:每一行的主元上方元素都为零。
即:
1.是行阶梯形矩阵;2.非0行的首非0元是1;3.非0行的首非0元所在列的其它元素都是0
红色折线表示矩阵为行阶梯形矩阵;蓝色圆圈表示首非0元是1;黄色竖线表示首非0元所在列的其它元素都是0
例子:
有矩阵A
( 2 − 1 − 1 1 2 1 1 − 2 1 4 4 − 6 2 − 2 4 3 6 − 9 7 9 ) \begin{pmatrix} 2 & -1 & -1 & 1 & 2 \\ 1 & 1 & -2 & 1 & 4\\ 4 & -6 & 2 & -2 & 4\\ 3 & 6 & -9 & 7 & 9\end{pmatrix} 2143−11−66−1−22−911−272449
求该矩阵的行阶梯形矩阵和行简化阶梯形矩阵
解:
1.第1行和第2行交换,得到
( 1 1 − 2 1 4 2 − 1 − 1 1 2 4 − 6 2 − 2 4 3 6 − 9 7 9 ) \begin{pmatrix} 1 & 1 & -2 & 1 & 4\\ 2 & -1 & -1 & 1 & 2 \\ 4 & -6 & 2 & -2 & 4\\ 3 & 6 & -9 & 7 & 9\end{pmatrix} 12431−1−66−2−12−911−274249
2.第1行乘以-2加到第2行,第1行乘以-4加到第3行,第1行乘以-3加到第4行,得到
( 1 1 − 2 1 4 0 − 3 3 − 1 − 6 0 − 10 10 − 6 − 12 0 3 − 3 4 − 3 ) \begin{pmatrix} 1 & 1 & -2 & 1 & 4\\ 0 & -3 & 3 & -1 & -6 \\ 0 & -10 & 10 & -6 & -12\\ 0 & 3 & -3 & 4 & -3\end{pmatrix} 10001−3−103−2310−31−1−644−6−12−3
3.第2行乘以-10/3加到第3行,第2行加到第4行,得到
( 1 1 − 2 1 4 0 − 3 3 − 1 − 6 0 0 0 − 8 3 8 0 0 0 3 − 9 ) \begin{pmatrix} 1 & 1 & -2 & 1 & 4\\ 0 & -3 & 3 & -1 & -6 \\ 0 & 0 & 0 & -\dfrac{8}{3} & 8\\ 0 & 0 & 0 & 3 & -9\end{pmatrix} 10001−300−23001−1−3834−68−9
4.第3三行乘以3/8,得到
( 1 1 − 2 1 4 0 − 3 3 − 1 − 6 0 0 0 − 1 3 0 0 0 3 − 9 ) \begin{pmatrix} 1 & 1 & -2 & 1 & 4\\ 0 & -3 & 3 & -1 & -6 \\ 0 & 0 & 0 & -1 & 3\\ 0 & 0 & 0 & 3 & -9\end{pmatrix} 10001−300−23001−1−134−63−9
5.第3行乘以3加到第4行,得到一个阶梯形矩阵
( 1 1 − 2 1 4 0 − 3 3 − 1 − 6 0 0 0 − 1 3 0 0 0 0 0 ) \begin{pmatrix} 1 & 1 & -2 & 1 & 4\\ 0 & -3 & 3 & -1 & -6 \\ 0 & 0 & 0 & -1 & 3\\ 0 & 0 & 0 & 0 & 0\end{pmatrix} 10001−300−23001−1−104−630
6.第三行乘以-1,得到
( 1 1 − 2 1 4 0 − 3 3 − 1 − 6 0 0 0 1 − 3 0 0 0 0 0 ) \begin{pmatrix} 1 & 1 & -2 & 1 & 4\\ 0 & -3 & 3 & -1 & -6 \\ 0 & 0 & 0 & 1 & -3\\ 0 & 0 & 0 & 0 & 0\end{pmatrix} 10001−300−23001−1104−6−30
7.第3行乘以-1加到第1行,第3行加到第2行
( 1 1 − 2 0 7 0 − 3 3 0 − 9 0 0 0 1 − 3 0 0 0 0 0 ) \begin{pmatrix} 1 & 1 & -2 & 0 & 7\\ 0 & -3 & 3 & 0 & -9 \\ 0 & 0 & 0 & 1 & -3\\ 0 & 0 & 0 & 0 & 0\end{pmatrix} 10001−300−230000107−9−30
8.第2行乘以1/3加到第1行,得到
( 1 0 − 1 0 4 0 − 3 3 0 − 9 0 0 0 1 − 3 0 0 0 0 0 ) \begin{pmatrix} 1 & 0 & -1 & 0 & 4\\ 0 & -3 & 3 & 0 & -9 \\ 0 & 0 & 0 & 1 & -3\\ 0 & 0 & 0 & 0 & 0\end{pmatrix} 10000−300−130000104−9−30
9.第2行乘以-1/3,得到一个行简化阶梯形矩阵
( 1 0 − 1 0 4 0 1 − 1 0 3 0 0 0 1 − 3 0 0 0 0 0 ) \begin{pmatrix} 1 & 0 & -1 & 0 & 4\\ 0 & 1 & -1 & 0 & 3 \\ 0 & 0 & 0 & 1 & -3\\ 0 & 0 & 0 & 0 & 0\end{pmatrix} 10000100−1−100001043−30
思考:行阶梯形矩阵是唯一的吗?行简化阶梯形矩阵是唯一的吗?
行阶梯形矩阵不是唯一的,上边例子中第5、6、7步得到的矩阵都是行阶梯形矩阵
如果只做初等行变换,行简化阶梯形矩阵是唯一的,因为不能再简化了
相关文章:
)
10.12Python数学基础-矩阵(下)
9.矩阵的转置 矩阵的转置(Transpose)是矩阵操作中的一种基本运算。它通过交换矩阵的行和列来生成一个新的矩阵。具体来说,如果 A 是一个 mn 的矩阵,那么它的转置矩阵 A^T 是一个 nm 的矩阵,其中 A^T 的第 i 行第 j 列…...

vue网络自学知识点汇总
初体验 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title><!--1.引入vue.j…...
)
Springboot项目Activemq延迟自定义消息完整代码案例(亲测可用)
1、porm.xml增加依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-activemq</artifactId> </dependency> 2、application.properties增加配置 # 连接地址 spring.activemq.broker-url=fa…...
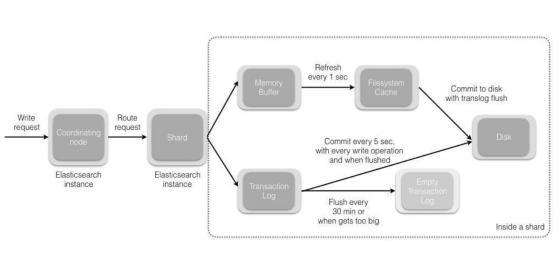
常见ElasticSearch 面试题解析(上)
前言 ElasticSearch是一个基于Lucene的搜索服务器。它提供了一个分布式多用户能力的全文搜索引擎,基于RESTful web接口。Elasticsearch是用Java语言开发的,并作为Apache许可条款下的开放源码发布,是一种流行的企业级搜索引擎。ElasticSearch…...
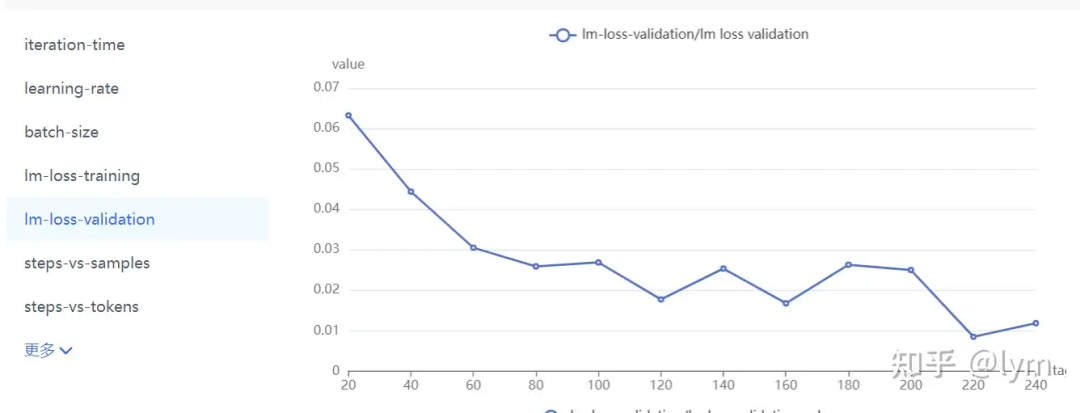
训练VLM(视觉语言模型)的经验
知乎:lym 链接:https://zhuanlan.zhihu.com/p/890327005 如果可以用prompt解决,尽量用prompt解决,因为训练(精调)的模型往往通用能力会下降,训练和长期部署成本都比较高,这个成本也包…...

犬儒乐队热歌《阶梯》主观
犬儒乐队一直以来是中国独立音乐界的一支重要力量。他们的音乐作品总是充满创意与实验,擅长将不同的音乐元素融合在一起,给人带来耳目一新的感受。最近,犬儒乐队发布了一首新歌《阶梯》,让我们一起来评价一下这首作品。 首先&…...

多模态大语言模型(MLLM)-Blip3/xGen-MM
论文链接:https://www.arxiv.org/abs/2408.08872 代码链接:https://github.com/salesforce/LAVIS/tree/xgen-mm 本次解读xGen-MM (BLIP-3): A Family of Open Large Multimodal Models 可以看作是 [1] Blip: Bootstrapping language-image pre-training…...

flutter TabBar自定义指示器(带文字的指示器、上弦弧形指示器、条形背景指示器、渐变色的指示器)
带文字的TabBar指示器 1.绘制自定义TabBar的绿色带白色文字的指示器 2.将底部灰色文字与TabrBar层叠,并调整高度位置与胶囊指示器重叠 自定义的带文字的TabBar指示器 import package:atui/jade/utils/JadeColors.dart; import package:flutter/material.dart; im…...

【Fargo】9:模拟图片采集的内存泄漏std::bad_alloc
std::bad_alloc 崩溃。这样的内存分配会导致内存耗尽 is simulating an image of size 640x480 with 3 bytes per pixel, resulting in an allocation of approximately 921,600 bytes (or around 900 KB) for each image. The error you’re encountering (std::bad_alloc) ty…...

c# 前端无插件打印导出实现方式
打印 打印导出分布页 model List<界面的数据模型类> using WingSoft; using Newtonsoft.Json; <style type"text/css">.modal-content {width: 800px;}.modal-body {height: 400px;} </style> <script type"text/javascript">$(…...

数组的初始化,参数传递,和求和
在自己做的这个C语言解释器中,数组的使用非常简便。下面小程序是一个例子。演示了数组的初始化,参数传递, 和求和。 all[] { WA12,OR8,CA54, ID4, MT4, WY3, NV6, UT6, AZ11, CO10, NM5, ND3,SD3,NE4, KS6, OK7,TX40, MN10, WI10,IA6, MO10,…...

初始JavaEE篇——多线程(1):Thread类的介绍与使用
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程(ಥ_ಥ)-CSDN博客 所属专栏:JavaEE 目录 创建线程 1、继承 Thread类 2、实现Runnable接口 3、使用匿名内部类 1)继承Thread类的匿名内部类 2)…...

基于单片机的LED照明自动控制系统的设计
本设计主控核心芯片选用了AT89C51单片机,接入了光照采集模块、红外感应模块、继电器控制模块,通过控制发光二极管模拟教室智能灯组的控制。首先通过光敏感应的方式感应当前光照环境为白天还是夜晚,同时,红外感应模块感应是否有人。…...

C语言——头文件的使用
目录 前言头文件怎么包含 前言 这个专栏会专门讲一些C语言的知识,后续会慢慢更新,欢迎关注 C语言专栏 头文件怎么包含 在使用头文件的过程中,我们经常会遇到重定义、重复包含等问题,那么怎么编写头文件和使用头文件才能解决这些…...

LeetCode 精选 75 回顾
目录 一、数组 / 字符串 1.交替合并字符串 (简单) 2.字符串的最大公因子 (简单) 3.拥有最多糖果的孩子(简单) 4.种花问题(简单) 5.反转字符串中的元音字母(简单&a…...

【Unity - 屏幕截图】技术要点
在Unity中想要实现全屏截图或者截取某个对象区域的图片都是可以通过下面的函数进行截取 Texture2D/// <summary>/// <para>Reads the pixels from the current render target (the screen, or a RenderTexture), and writes them to the texture.</para>/…...

句句深刻,字字经典,创客匠人老蒋金句出炉,哪一句让你醍醐灌顶?
注意力经济时代、流量经济时代、短视频经济时代,创始人到底应该如何做,才能抓住风口,链接未来? 「创始人IP创新增长班」线下大课现场,老蒋作为主讲导师,再一次用他丰富的行业经验与深刻的时代洞察ÿ…...

柯尼卡美能达CA-310 FPD色彩分析仪
柯尼卡美能达CA-310 FPD色彩分析仪 型 号:CA-310 名 称:FPD色彩分析仪 品 牌:柯尼卡美能达(KONICA MINOLTA) 分 类:光学和色彩测试 > 光学、显示与色彩测量 > 色彩分析仪 产品属性:主机 简 述&…...

二维EKF的MATLAB代码
EKF二维滤波 MATLAB 实现 提升您的数据处理能力!本MATLAB程序实现了扩展卡尔曼滤波(EKF)在二维状态估计中的应用,专为需要高精度定位和动态系统分析的用户设计。通过精确的滤波技术,有效减少噪声影响,确保…...

大数据治理:数据时代的挑战与应对
目录 大数据治理:数据时代的挑战与应对 一、大数据治理的概念与内涵 二、大数据治理的重要性 1. 提高数据质量与可用性 2. 确保数据安全与合规 3. 支持数据驱动的决策 4. 提高业务效率与竞争力 三、大数据治理的实施策略 1. 建立健全的数据治理框架 2. 数…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
